2020——2021学年北师大版数学九下第1章 6 利用三角函数测高同步检测(word版含解析)
文档属性
| 名称 | 2020——2021学年北师大版数学九下第1章 6 利用三角函数测高同步检测(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 494.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 20:06:41 | ||
图片预览




文档简介
第1章
6
利用三角函数测高
一、选择题(共20分)
1.
年
月
日,深圳市民中心及周边楼宇为当日返回深圳的援鄂医疗队员亮灯,欢迎最美逆行者回家.小洪在欢迎英雄回家现场,如图,若他观测到英雄画像电子屏顶端
和底端
的仰角分别为
和
,小洪所站位置
到电子屏边缘
垂直地面的
点距离为
米,那么英雄画像电子屏
高为
A.
米
B.
米
C.
米
D.
米
2.
如图,课外小组的同学们在校内准备测量墙外一手机发射塔
的高度,小组的同学们首先在校内宽敞处选定一点
,在
点测得到塔顶
的仰角为
,然后他们沿与
和塔底
连线
垂直的方向走了
米到达
点,在
点测得到塔顶
的仰角为
,小组根据这些数据计算出与发射塔的高度最接近的数值是
A.
B.
C.
D.
3.
如图,在离铁塔
米的
处,用测倾器测得塔顶的仰角为
,测倾器高
为
米,则铁塔的高
为
A.
米
B.
米
C.
米
D.
米
4.
小明同学想要测量如图所示的仙女峰的高度,他利用已学的数学知识设计了一个实践方案,并实施了如下操作:先在水平地面
处测得山顶
的仰角
为
,再由
沿水平方向前进
米到达山脚
处,测得山坡
的坡度为
,那么仙女峰的高度约为(参考数据
)
A.
米
B.
米
C.
米
D.
米
5.
小菁同学在数学实践活动课中测量路灯的高度.如图,已知她的身高
为
米,她先站在
处看路灯顶端
的仰角为
,再往前走
米站在
处,看路灯顶端
的仰角为
,则路灯顶端
到地面的距离约为(已知
,,,,,)
A.
米
B.
米
C.
米
D.
米
二、解答题(共10小题;共100分)
6.
在数学综合实践活动课上,某小组要测量学校升旗台旗杆顶端离地面的高度.如图,测得
,斜坡
的长为
米,坡度
,在点
处测得旗杆顶端的仰角为
,点
到旗杆底部
的距离为
米.
(参考数据:,,)
(1)求斜坡
的坡角
的度数;
(2)求旗杆顶端离地面的高度
.
7.
如图所示,平台
高
,在
处测得楼房
顶部点
的仰角为
,底部点
的俯角为
,求楼房
的高度.(结果取整数)(参考数据:,)
8.
“天空之城”摩天轮位于宁波市杭州湾新区欢乐世界.摩天轮高约
米(最高点到地面的距离).如图,点
是摩天轮的圆心,
是其垂直于地面的直径,小明在地面
处用测角仪测得摩天轮最高点
的仰角为
,测得圆心
的仰角为
,求摩天轮的半径.(结果保留根号)
9.
如图,为测量建筑物
的高度,在
点测得建筑物顶部
点的仰角为
,再向建筑物
前进
米到达
点,测得建筑物顶部
点的仰角为
(,,
三点在一条直线上),求建筑物
的高度.(结果保留整数.参考数据:,,,,,)
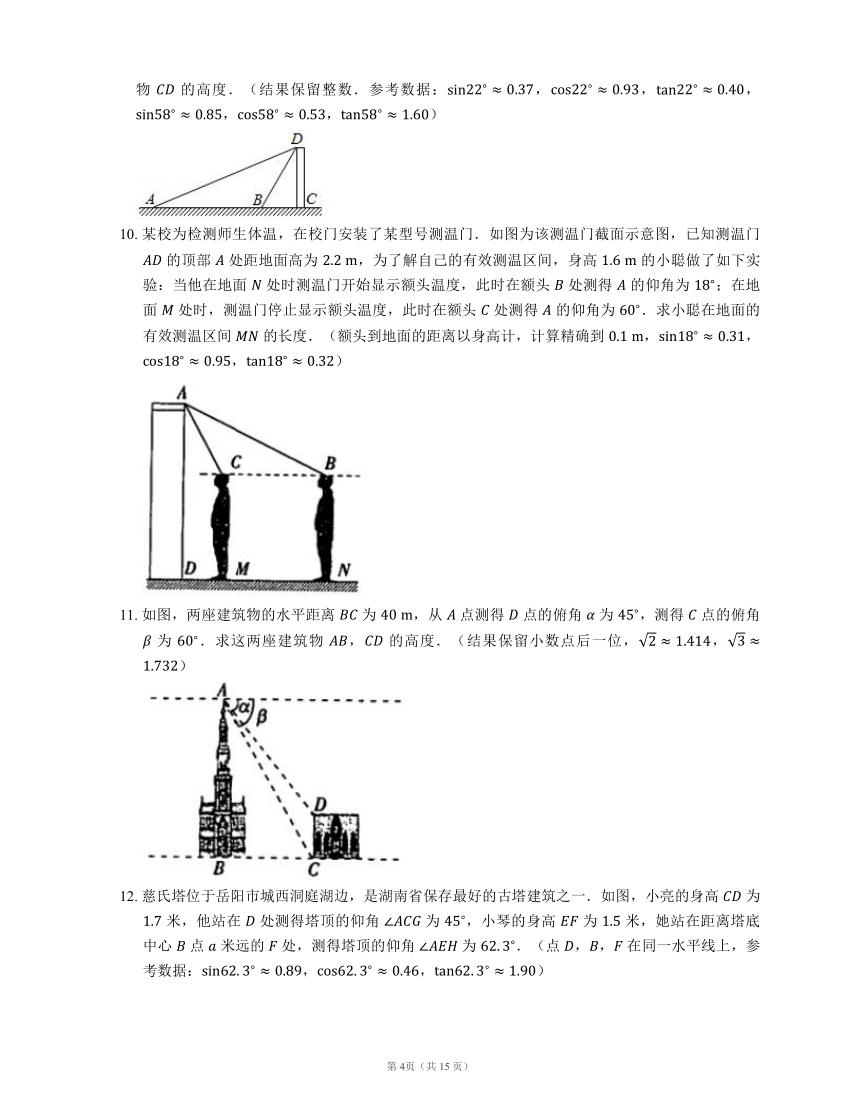
10.
某校为检测师生体温,在校门安装了某型号测温门.如图为该测温门截面示意图,已知测温门
的顶部
处距地面高为
,为了解自己的有效测温区间,身高
的小聪做了如下实验:当他在地面
处时测温门开始显示额头温度,此时在额头
处测得
的仰角为
;在地面
处时,测温门停止显示额头温度,此时在额头
处测得
的仰角为
.求小聪在地面的有效测温区间
的长度.(额头到地面的距离以身高计,计算精确到
,,,)
11.
如图,两座建筑物的水平距离
为
,从
点测得
点的俯角
为
,测得
点的俯角
为
.求这两座建筑物
,
的高度.(结果保留小数点后一位,,)
12.
慈氏塔位于岳阳市城西洞庭湖边,是湖南省保存最好的古塔建筑之一.如图,小亮的身高
为
米,他站在
处测得塔顶的仰角
为
,小琴的身高
为
米,她站在距离塔底中心
点
米远的
处,测得塔顶的仰角
为
.(点
,,
在同一水平线上,参考数据:,,)
(1)求小亮与塔底中心的距离
;(用含
的式子表示)
(2)若小亮与小琴相距
米,求慈氏塔的高度
.
13.
某“综合与实践”小组开展了测量本校旗杆高度的实践活动.他们制定了测量方案,并利用课余时间完成了实地测量.他们在该旗杆底部所在的平地上,选取两个不同测点,分别测量了该旗杆顶端的仰角以及这两个测点之间的距离.为了减小测量误差,小组在测量仰角的度数以及两个测点之间的距离时,都分别测量了两次并取它们的平均值作为测量结果,测量数据如下表(不完整):
(参考数据:,,,,,)
(1)两次测量
,
之间的距离的平均值是
?
;
(2)根据以上测量结果,请你帮助该“综合与实践”小组求出学校旗杆
的高度;
(3)该“综合与实践”小组在制定方案时,讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案,但未被采纳.你认为其原因可能是什么?(写出一条即可)
14.
如图,斜坡
的坡度为
,坡面长
米,,现计划在斜坡中点
处挖去部分坡体(用阴影表示)修建一个平行于水平线
的平台
和一条新的斜坡
.
(请将第()小题结果精确到
米,参考数据:)
(1)若修建的斜坡
的坡角(即
)恰为
,则此时平台
的长为
?米;
(2)坡前有一建筑物
,小明在
点测得建筑物顶部
的仰角为
,在坡底
点测得建筑物顶部
的仰角为
,点
,,,,
在同一平面内,点
,,
在同一条水平直线上,问建筑物
高为多少米?
15.
关于三角函数有如下公式:
,
,
,
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值,如:
根据上面的知识,你可以选择适当的公式解决下面的实际问题:
如图,直升机在一建筑物
上方
点处测得建筑物顶端
点的俯角
为
,底端
点的俯角
为
.此时直升机与建筑物
的水平距离
为
米,求建筑物
的高.
答案
第一部分
1.
C
【解析】根据题意得
,
在
中,
,
,
在
中,
,
,
米,
英雄画像电子屏
高为
米.
2.
D
【解析】设
米,在
中,,
米,
在
中,
,
米,
在
中,,
米,
,
解得
.
3.
A
【解析】过点
作
,
为垂足,如图所示,
则四边形
为矩形,
所以
,,
在
中,因为
,
所以
,
所以
米.
4.
B
【解析】如图,过点
作
,交
的延长线于点
,
山坡
的坡度为
,
,则
,
为
,
,
,
,
解得
(米).
故选B.
5.
C
【解析】如图,过点
作
,交
的延长线于点
,延长
交
于点
,
设
米,
米,
,
米,
,
米,
,
,
(米),
(米),
故路灯顶端
到地面的距离约为
米.
故选C.
第二部分
6.
(1)
如图所示,过点
作
于点
,
,
,
即
.
????(2)
,,
,
在
中,
,,
,
则
(米).
答:旗杆顶端离地面的高度
约为
米.
7.
过点
作
,垂足为
,
在
中,,,,
,
在
中,,,
.
答:楼房
的高度约为
.
8.
如图,延长
与地面所在直线交于点
,
根据题意可知
,
,
,
,
,
在
中,,
,
,
米.
答:摩天轮的半径为
米.
9.
在
中,
,
,
,
在
中,
,
,
,
,解得:(米).
答:建筑物
的高度为
米.
10.
延长
交
于点
,
则
,
在
中,,
在
中,,
所以
,
所以
.
答:小聪在地面的有效测温区间
的长度约为
.
11.
如图,延长
交
于点
,
则
,
在
中,,,
,
在
中,,,
,
则
.
答:这两座建筑物
,
的高度分别约为
和
.
12.
(1)
由题意得,四边形
、四边形
为矩形,
,,
.
在
中,,
则
,
,
在
中,,
,
米.
答:小亮与塔底中心的距离
为
米.
??????(2)
由题意得,,解得
,
则
,
(米).
答:慈氏塔的高度
为
米.
13.
(1)
【解析】由题意可得,两次测量
,
之间的距离的平均值是
.
??????(2)
设
,在
中,,,
,
.
在
中,,,
,
,
,
,
,
.
答:学校旗杆
的高度约为
.
??????(3)
答案不唯一,如:没有太阳光或旗杆底部不可能到达等.
14.
(1)
【解析】
斜坡
的坡度为
,
,
设
为
米,则
为
米,
在
中,
米,
,
解得
(舍负),
米,
米,
为
的中点,,,
米,
米,
故
(米),
则平台
的长为
米,
故答案为
.
??????(2)
过点
作
,,垂足分别为
,,
易得
米,
米,
设
米,在矩形
中,
米,
米,
在
中,
米,
米,
,
,
解得
,
(米).
答:建筑物
高约为
米.
15.
如图,过点
作
于点
.
在
中,,
米.
在
中,,
.
,
米,
(米).
答:建筑物
的高为
米.
第1页(共15
页)
6
利用三角函数测高
一、选择题(共20分)
1.
年
月
日,深圳市民中心及周边楼宇为当日返回深圳的援鄂医疗队员亮灯,欢迎最美逆行者回家.小洪在欢迎英雄回家现场,如图,若他观测到英雄画像电子屏顶端
和底端
的仰角分别为
和
,小洪所站位置
到电子屏边缘
垂直地面的
点距离为
米,那么英雄画像电子屏
高为
A.
米
B.
米
C.
米
D.
米
2.
如图,课外小组的同学们在校内准备测量墙外一手机发射塔
的高度,小组的同学们首先在校内宽敞处选定一点
,在
点测得到塔顶
的仰角为
,然后他们沿与
和塔底
连线
垂直的方向走了
米到达
点,在
点测得到塔顶
的仰角为
,小组根据这些数据计算出与发射塔的高度最接近的数值是
A.
B.
C.
D.
3.
如图,在离铁塔
米的
处,用测倾器测得塔顶的仰角为
,测倾器高
为
米,则铁塔的高
为
A.
米
B.
米
C.
米
D.
米
4.
小明同学想要测量如图所示的仙女峰的高度,他利用已学的数学知识设计了一个实践方案,并实施了如下操作:先在水平地面
处测得山顶
的仰角
为
,再由
沿水平方向前进
米到达山脚
处,测得山坡
的坡度为
,那么仙女峰的高度约为(参考数据
)
A.
米
B.
米
C.
米
D.
米
5.
小菁同学在数学实践活动课中测量路灯的高度.如图,已知她的身高
为
米,她先站在
处看路灯顶端
的仰角为
,再往前走
米站在
处,看路灯顶端
的仰角为
,则路灯顶端
到地面的距离约为(已知
,,,,,)
A.
米
B.
米
C.
米
D.
米
二、解答题(共10小题;共100分)
6.
在数学综合实践活动课上,某小组要测量学校升旗台旗杆顶端离地面的高度.如图,测得
,斜坡
的长为
米,坡度
,在点
处测得旗杆顶端的仰角为
,点
到旗杆底部
的距离为
米.
(参考数据:,,)
(1)求斜坡
的坡角
的度数;
(2)求旗杆顶端离地面的高度
.
7.
如图所示,平台
高
,在
处测得楼房
顶部点
的仰角为
,底部点
的俯角为
,求楼房
的高度.(结果取整数)(参考数据:,)
8.
“天空之城”摩天轮位于宁波市杭州湾新区欢乐世界.摩天轮高约
米(最高点到地面的距离).如图,点
是摩天轮的圆心,
是其垂直于地面的直径,小明在地面
处用测角仪测得摩天轮最高点
的仰角为
,测得圆心
的仰角为
,求摩天轮的半径.(结果保留根号)
9.
如图,为测量建筑物
的高度,在
点测得建筑物顶部
点的仰角为
,再向建筑物
前进
米到达
点,测得建筑物顶部
点的仰角为
(,,
三点在一条直线上),求建筑物
的高度.(结果保留整数.参考数据:,,,,,)
10.
某校为检测师生体温,在校门安装了某型号测温门.如图为该测温门截面示意图,已知测温门
的顶部
处距地面高为
,为了解自己的有效测温区间,身高
的小聪做了如下实验:当他在地面
处时测温门开始显示额头温度,此时在额头
处测得
的仰角为
;在地面
处时,测温门停止显示额头温度,此时在额头
处测得
的仰角为
.求小聪在地面的有效测温区间
的长度.(额头到地面的距离以身高计,计算精确到
,,,)
11.
如图,两座建筑物的水平距离
为
,从
点测得
点的俯角
为
,测得
点的俯角
为
.求这两座建筑物
,
的高度.(结果保留小数点后一位,,)
12.
慈氏塔位于岳阳市城西洞庭湖边,是湖南省保存最好的古塔建筑之一.如图,小亮的身高
为
米,他站在
处测得塔顶的仰角
为
,小琴的身高
为
米,她站在距离塔底中心
点
米远的
处,测得塔顶的仰角
为
.(点
,,
在同一水平线上,参考数据:,,)
(1)求小亮与塔底中心的距离
;(用含
的式子表示)
(2)若小亮与小琴相距
米,求慈氏塔的高度
.
13.
某“综合与实践”小组开展了测量本校旗杆高度的实践活动.他们制定了测量方案,并利用课余时间完成了实地测量.他们在该旗杆底部所在的平地上,选取两个不同测点,分别测量了该旗杆顶端的仰角以及这两个测点之间的距离.为了减小测量误差,小组在测量仰角的度数以及两个测点之间的距离时,都分别测量了两次并取它们的平均值作为测量结果,测量数据如下表(不完整):
(参考数据:,,,,,)
(1)两次测量
,
之间的距离的平均值是
?
;
(2)根据以上测量结果,请你帮助该“综合与实践”小组求出学校旗杆
的高度;
(3)该“综合与实践”小组在制定方案时,讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案,但未被采纳.你认为其原因可能是什么?(写出一条即可)
14.
如图,斜坡
的坡度为
,坡面长
米,,现计划在斜坡中点
处挖去部分坡体(用阴影表示)修建一个平行于水平线
的平台
和一条新的斜坡
.
(请将第()小题结果精确到
米,参考数据:)
(1)若修建的斜坡
的坡角(即
)恰为
,则此时平台
的长为
?米;
(2)坡前有一建筑物
,小明在
点测得建筑物顶部
的仰角为
,在坡底
点测得建筑物顶部
的仰角为
,点
,,,,
在同一平面内,点
,,
在同一条水平直线上,问建筑物
高为多少米?
15.
关于三角函数有如下公式:
,
,
,
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值,如:
根据上面的知识,你可以选择适当的公式解决下面的实际问题:
如图,直升机在一建筑物
上方
点处测得建筑物顶端
点的俯角
为
,底端
点的俯角
为
.此时直升机与建筑物
的水平距离
为
米,求建筑物
的高.
答案
第一部分
1.
C
【解析】根据题意得
,
在
中,
,
,
在
中,
,
,
米,
英雄画像电子屏
高为
米.
2.
D
【解析】设
米,在
中,,
米,
在
中,
,
米,
在
中,,
米,
,
解得
.
3.
A
【解析】过点
作
,
为垂足,如图所示,
则四边形
为矩形,
所以
,,
在
中,因为
,
所以
,
所以
米.
4.
B
【解析】如图,过点
作
,交
的延长线于点
,
山坡
的坡度为
,
,则
,
为
,
,
,
,
解得
(米).
故选B.
5.
C
【解析】如图,过点
作
,交
的延长线于点
,延长
交
于点
,
设
米,
米,
,
米,
,
米,
,
,
(米),
(米),
故路灯顶端
到地面的距离约为
米.
故选C.
第二部分
6.
(1)
如图所示,过点
作
于点
,
,
,
即
.
????(2)
,,
,
在
中,
,,
,
则
(米).
答:旗杆顶端离地面的高度
约为
米.
7.
过点
作
,垂足为
,
在
中,,,,
,
在
中,,,
.
答:楼房
的高度约为
.
8.
如图,延长
与地面所在直线交于点
,
根据题意可知
,
,
,
,
,
在
中,,
,
,
米.
答:摩天轮的半径为
米.
9.
在
中,
,
,
,
在
中,
,
,
,
,解得:(米).
答:建筑物
的高度为
米.
10.
延长
交
于点
,
则
,
在
中,,
在
中,,
所以
,
所以
.
答:小聪在地面的有效测温区间
的长度约为
.
11.
如图,延长
交
于点
,
则
,
在
中,,,
,
在
中,,,
,
则
.
答:这两座建筑物
,
的高度分别约为
和
.
12.
(1)
由题意得,四边形
、四边形
为矩形,
,,
.
在
中,,
则
,
,
在
中,,
,
米.
答:小亮与塔底中心的距离
为
米.
??????(2)
由题意得,,解得
,
则
,
(米).
答:慈氏塔的高度
为
米.
13.
(1)
【解析】由题意可得,两次测量
,
之间的距离的平均值是
.
??????(2)
设
,在
中,,,
,
.
在
中,,,
,
,
,
,
,
.
答:学校旗杆
的高度约为
.
??????(3)
答案不唯一,如:没有太阳光或旗杆底部不可能到达等.
14.
(1)
【解析】
斜坡
的坡度为
,
,
设
为
米,则
为
米,
在
中,
米,
,
解得
(舍负),
米,
米,
为
的中点,,,
米,
米,
故
(米),
则平台
的长为
米,
故答案为
.
??????(2)
过点
作
,,垂足分别为
,,
易得
米,
米,
设
米,在矩形
中,
米,
米,
在
中,
米,
米,
,
,
解得
,
(米).
答:建筑物
高约为
米.
15.
如图,过点
作
于点
.
在
中,,
米.
在
中,,
.
,
米,
(米).
答:建筑物
的高为
米.
第1页(共15
页)
