6.1.1函数的平均变化率-【新教材】2020-2021学年人教B版(2019)高中数学选择性必修第三册课时练习Word含解析
文档属性
| 名称 | 6.1.1函数的平均变化率-【新教材】2020-2021学年人教B版(2019)高中数学选择性必修第三册课时练习Word含解析 |

|
|
| 格式 | doc | ||
| 文件大小 | 629.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 00:00:00 | ||
图片预览




文档简介
6.1.1函数的平均变化率课时作业1
A级 巩固基础
一、单选题
1.设函数,当自变量由1变到1.1时,函数的平均变化率是( )
A.2.1 B.0.21 C.1.21 D.0.121
2.甲、乙两厂污水的排放量W与时间的关系如图所示,则治污效果较好的是( )
A.甲厂 B.乙厂 C.两厂一样 D.不确定
3.已知函数和在区间上的图象如图所示,则下列说法正确的是( )
A.在a到b之间的平均变化率大于在a到b之间的平均变化率
B.在a到b之间的平均变化率小于在a到b之间的平均变化率
C.对于任意,函数在处的瞬时变化率总大于函数在处的瞬时变化率
D.存在,使得函数在处的瞬时变化率小于函数在处的瞬时变化率
4.已知函数图象上四点、、、,割线、、的斜率分别为,则( )
A. B. C. D.
5.一质点的运动方程是,则在时间内相应的平均速度为( )
A. B. C. D.
6.某质点的运动规律为,则在时间内,质点的位移增量等于( )
A. B. C. D.
7.函数区间上的平均变化率为( )
A.2 B.4 C.c D.2c
8.函数在处的瞬时变化率为( )
A.2 B. C. D.1
B级 综合应用
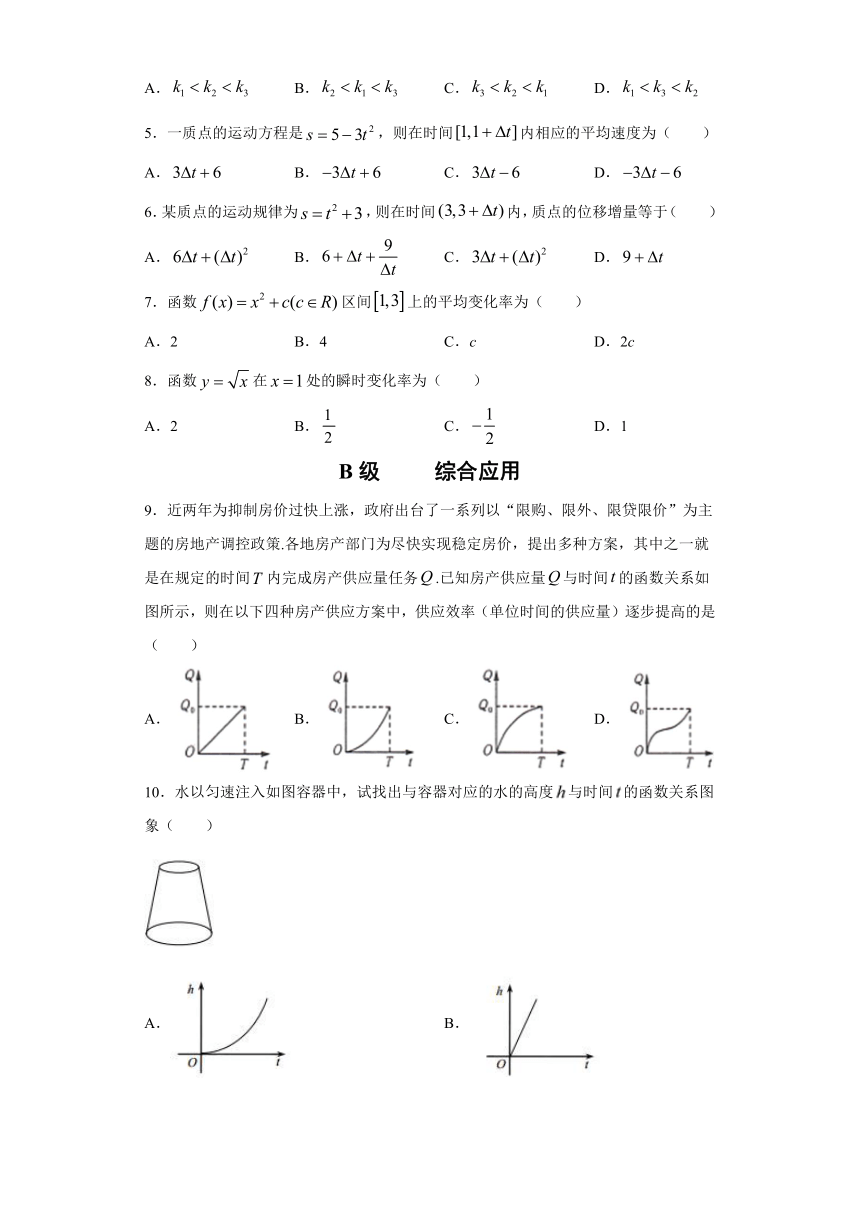
9.近两年为抑制房价过快上涨,政府出台了一系列以“限购、限外、限贷限价”为主题的房地产调控政策.各地房产部门为尽快实现稳定房价,提出多种方案,其中之一就是在规定的时间内完成房产供应量任务.已知房产供应量与时间的函数关系如图所示,则在以下四种房产供应方案中,供应效率(单位时间的供应量)逐步提高的是( )
A. B. C. D.
10.水以匀速注入如图容器中,试找出与容器对应的水的高度与时间的函数关系图象( )
A. B.
C. D.
二、填空题
11.函数在区间上的平均变化率为_________.
12.函数在区间[1,m]上的平均变化率为3,则实数m的值为___________.
13.函数在区间上的平均变化率为__________.
14.函数在区间上的平均变化率为____________.
15.已知物体运动的速度与时间之间的关系是,则在时间间隔内的平均加速度是______.
C级 拓展探究
三、解答题
16.(1)计算函数从到的平均变化率,其中的值为:①2;②1;0.1;④0.01
(2)思考:当越来越小时,函数在区间上的平均变化率有怎样的变化趋势?
参考答案
1.A
【分析】
根据平均变化率的公式求解即可.
【详解】
,
所以函数在区间上的平均变化率为.
故选:A
2.B
【分析】
比较与、与的大小关系,可比较出两厂的平均治污率的大小关系,由此可得出结论.
【详解】
在处,虽然有,但,
所以在相同时间内,甲厂比乙厂的平均治污率小,所以乙厂治污效果较好.
故选:B.
3.D
【分析】
由平均变化率和瞬时变化率的概念即可判断.
【详解】
解:∵在a到b之间的平均变化率是,
在a到b之间的平均变化率是,
又,,
∴,
∴A、B错误;
易知函数在处的瞬时变化率是函数在处的导数,
即函数在该点处的切线的斜率,
同理可得:函数在处的瞬时变化率是函数在该点处的导数,
即函数在该点处的切线的斜率,
由题中图象可知:
时,函数在处切线的斜率有可能大于在处切线的斜率,也有可能小于在处切线的斜率,故C错误,D正确.
故选:D.
4.A
【分析】
由斜率公式计算出斜率后比较可得.
【详解】
,,,
∴,
故选:A.
5.D
【分析】
由平均变化率的定义计算.
【详解】
.
故选:D.
6.A
【分析】
根据平均变化率的定义计算.
【详解】
位移增量.
故选:A.
7.B
【分析】
根据函数的平均变化率的公式,求解即可.
【详解】
故选:B
【点睛】
求平均变化率的方法:利用公式.
8.B
【分析】
函数在某点处的瞬时变化率即为函数在改点的导数值,求导得解
【详解】
,
所以函数在处的瞬时变化率为
故选:B
【点睛】
本题考查函数在某点处的导数值,属于基础题.
9.B
【分析】
根据变化率的知识,结合曲线在某点处导数的几何意义,可得结果.
【详解】
单位时间的供应量逐步提高时,供应量的增长
速度越来越快,图象上切线的斜率随着自变量
的增加会越来越大,则曲线是上升的,且越来越陡,
故函数的图象应一直下凹的.
故选B.
【点睛】
本题考查变化率的知识,实质上是考查曲线在某点处导数的几何意义,属基础题.
10.A
【解析】
试题分析:由于容器上细下粗,所以水以横速注入水,开始阶段高度增加的慢,以后高度增加的越来越快,因此与图象越来越陡峭,原来越大,选
考点:函数的单调性与导数的关系.
11.
【分析】
根据平均变化率的公式进行求解即可.
【详解】
函数在区间上的平均变化率为:.
故答案为:
12.
【分析】
由函数的平均变化率公式,建立的方程,即可求解.
【详解】
函数在区间[1,m]上的平均变化率为
.
故答案为:.
【点睛】
本题考查函数的变化率,属于基础题.
13.2
【分析】
根据平均变化率定义计算.
【详解】
.
故答案为:2.
【点睛】
本题考查平均变化率的概念,属于基础题.
14.1
【分析】
根据平均变化率的概念,得到,简单计算,可得结果.
【详解】
故答案为:1
【点睛】
本题考查平均变化率的概念,属基础题.
15.
【分析】
利用平均变化率知该物体在时间间隔内的平均加速度为,代入进行计算即可.
【详解】
由平均变化率的定义可知,该物体在内的平均加速度为,故答案为.
【点睛】
本题考查平均加速度的计算,解题的关键就是利用平均变化率的定义进行计算,考查计算能力,属于基础题.
16.(1)答案见解析;(2)平均变化率逐渐变小,并接近于2
【分析】
(1)利用平均变化率的意义即可得出;
(2)观察平均变化率即可得结果.
【详解】
(1)因为
所以.
①当时,;
②当时,;
③当时,;
④当时,.
(2)当越来越小时,
由(1)得,
函数在区间上的平均变化率逐渐变小,并接近于2.
【点睛】
本题考查平均变化率的求解,是基础题.
A级 巩固基础
一、单选题
1.设函数,当自变量由1变到1.1时,函数的平均变化率是( )
A.2.1 B.0.21 C.1.21 D.0.121
2.甲、乙两厂污水的排放量W与时间的关系如图所示,则治污效果较好的是( )
A.甲厂 B.乙厂 C.两厂一样 D.不确定
3.已知函数和在区间上的图象如图所示,则下列说法正确的是( )
A.在a到b之间的平均变化率大于在a到b之间的平均变化率
B.在a到b之间的平均变化率小于在a到b之间的平均变化率
C.对于任意,函数在处的瞬时变化率总大于函数在处的瞬时变化率
D.存在,使得函数在处的瞬时变化率小于函数在处的瞬时变化率
4.已知函数图象上四点、、、,割线、、的斜率分别为,则( )
A. B. C. D.
5.一质点的运动方程是,则在时间内相应的平均速度为( )
A. B. C. D.
6.某质点的运动规律为,则在时间内,质点的位移增量等于( )
A. B. C. D.
7.函数区间上的平均变化率为( )
A.2 B.4 C.c D.2c
8.函数在处的瞬时变化率为( )
A.2 B. C. D.1
B级 综合应用
9.近两年为抑制房价过快上涨,政府出台了一系列以“限购、限外、限贷限价”为主题的房地产调控政策.各地房产部门为尽快实现稳定房价,提出多种方案,其中之一就是在规定的时间内完成房产供应量任务.已知房产供应量与时间的函数关系如图所示,则在以下四种房产供应方案中,供应效率(单位时间的供应量)逐步提高的是( )
A. B. C. D.
10.水以匀速注入如图容器中,试找出与容器对应的水的高度与时间的函数关系图象( )
A. B.
C. D.
二、填空题
11.函数在区间上的平均变化率为_________.
12.函数在区间[1,m]上的平均变化率为3,则实数m的值为___________.
13.函数在区间上的平均变化率为__________.
14.函数在区间上的平均变化率为____________.
15.已知物体运动的速度与时间之间的关系是,则在时间间隔内的平均加速度是______.
C级 拓展探究
三、解答题
16.(1)计算函数从到的平均变化率,其中的值为:①2;②1;0.1;④0.01
(2)思考:当越来越小时,函数在区间上的平均变化率有怎样的变化趋势?
参考答案
1.A
【分析】
根据平均变化率的公式求解即可.
【详解】
,
所以函数在区间上的平均变化率为.
故选:A
2.B
【分析】
比较与、与的大小关系,可比较出两厂的平均治污率的大小关系,由此可得出结论.
【详解】
在处,虽然有,但,
所以在相同时间内,甲厂比乙厂的平均治污率小,所以乙厂治污效果较好.
故选:B.
3.D
【分析】
由平均变化率和瞬时变化率的概念即可判断.
【详解】
解:∵在a到b之间的平均变化率是,
在a到b之间的平均变化率是,
又,,
∴,
∴A、B错误;
易知函数在处的瞬时变化率是函数在处的导数,
即函数在该点处的切线的斜率,
同理可得:函数在处的瞬时变化率是函数在该点处的导数,
即函数在该点处的切线的斜率,
由题中图象可知:
时,函数在处切线的斜率有可能大于在处切线的斜率,也有可能小于在处切线的斜率,故C错误,D正确.
故选:D.
4.A
【分析】
由斜率公式计算出斜率后比较可得.
【详解】
,,,
∴,
故选:A.
5.D
【分析】
由平均变化率的定义计算.
【详解】
.
故选:D.
6.A
【分析】
根据平均变化率的定义计算.
【详解】
位移增量.
故选:A.
7.B
【分析】
根据函数的平均变化率的公式,求解即可.
【详解】
故选:B
【点睛】
求平均变化率的方法:利用公式.
8.B
【分析】
函数在某点处的瞬时变化率即为函数在改点的导数值,求导得解
【详解】
,
所以函数在处的瞬时变化率为
故选:B
【点睛】
本题考查函数在某点处的导数值,属于基础题.
9.B
【分析】
根据变化率的知识,结合曲线在某点处导数的几何意义,可得结果.
【详解】
单位时间的供应量逐步提高时,供应量的增长
速度越来越快,图象上切线的斜率随着自变量
的增加会越来越大,则曲线是上升的,且越来越陡,
故函数的图象应一直下凹的.
故选B.
【点睛】
本题考查变化率的知识,实质上是考查曲线在某点处导数的几何意义,属基础题.
10.A
【解析】
试题分析:由于容器上细下粗,所以水以横速注入水,开始阶段高度增加的慢,以后高度增加的越来越快,因此与图象越来越陡峭,原来越大,选
考点:函数的单调性与导数的关系.
11.
【分析】
根据平均变化率的公式进行求解即可.
【详解】
函数在区间上的平均变化率为:.
故答案为:
12.
【分析】
由函数的平均变化率公式,建立的方程,即可求解.
【详解】
函数在区间[1,m]上的平均变化率为
.
故答案为:.
【点睛】
本题考查函数的变化率,属于基础题.
13.2
【分析】
根据平均变化率定义计算.
【详解】
.
故答案为:2.
【点睛】
本题考查平均变化率的概念,属于基础题.
14.1
【分析】
根据平均变化率的概念,得到,简单计算,可得结果.
【详解】
故答案为:1
【点睛】
本题考查平均变化率的概念,属基础题.
15.
【分析】
利用平均变化率知该物体在时间间隔内的平均加速度为,代入进行计算即可.
【详解】
由平均变化率的定义可知,该物体在内的平均加速度为,故答案为.
【点睛】
本题考查平均加速度的计算,解题的关键就是利用平均变化率的定义进行计算,考查计算能力,属于基础题.
16.(1)答案见解析;(2)平均变化率逐渐变小,并接近于2
【分析】
(1)利用平均变化率的意义即可得出;
(2)观察平均变化率即可得结果.
【详解】
(1)因为
所以.
①当时,;
②当时,;
③当时,;
④当时,.
(2)当越来越小时,
由(1)得,
函数在区间上的平均变化率逐渐变小,并接近于2.
【点睛】
本题考查平均变化率的求解,是基础题.
