6.1.2导数及其几何意义-【新教材】2020-2021学年人教B版(2019)高中数学选择性必修第三册课时练习Word含解析
文档属性
| 名称 | 6.1.2导数及其几何意义-【新教材】2020-2021学年人教B版(2019)高中数学选择性必修第三册课时练习Word含解析 |

|
|
| 格式 | doc | ||
| 文件大小 | 492.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 16:53:28 | ||
图片预览




文档简介
6.1.2导数及其几何意义课时作业2
A级 巩固基础
一、单选题
1.设,则曲线在点处的切线的倾斜角是( )
A. B. C. D.
2.设是可导函数,且,则( )
A.2 B. C.1 D.
3.如图,点A(x1,f(x1)),B(x2,f(x2))在函数f(x)的图象上,且x2<x1,为f(x)的导函数,则与的大小关系是( )
A. B.
C. D.不能确定
4.若(m为常数),则等于( )
A. B.1 C.m D.
5.某物体的运动方程为(位移单位:m,时间单位:s),若,则下列说法中正确的是( )
A.是物体从开始到这段时间内的平均速度
B.是物体从到这段时间内的速度
C.是物体在这一时刻的瞬时速度
D.是物体从到这段时间内的平均速度
6.已知函数在处的导数为1,则 ( )
A. B. C. D.
7.已知函数在处的导数为1,则( )
A.0 B. C.1 D.2
8.在高台跳水运动中时运动员相对于水面的高度(单位:)是,则高台跳水运动中运动员在时的瞬时速度是( )
A. B. C.13.1 D.3.3
B级 综合应用
9.函数在处的导数的几何意义是( )
A.在点处与的图象只有一个交点的直线的斜率
B.过点的切线的斜率
C.点与点的连线的斜率
D.函数的图象在点处的切线的斜率
10.已知函数f(x)的图象如图所示,下列数值的排序正确的是( )
A. B.
C. D.
11.函数在处的切线如图所示,则( )
A.0 B. C. D.
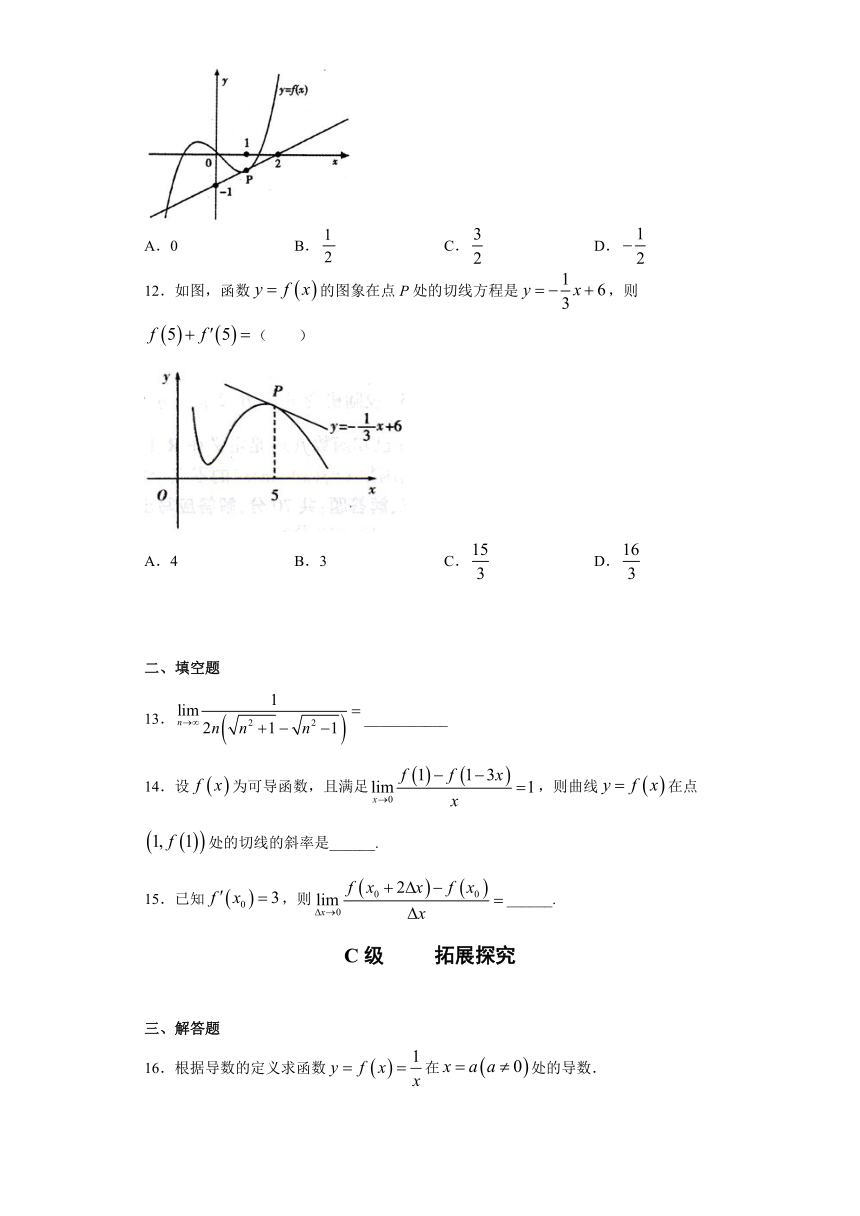
12.如图,函数的图象在点P处的切线方程是,则( )
A.4 B.3 C. D.
二、填空题
13.___________
14.设为可导函数,且满足,则曲线在点处的切线的斜率是______.
15.已知,则______.
C级 拓展探究
三、解答题
16.根据导数的定义求函数在处的导数.
参考答案
1.C
【分析】
根据导数的概念可得,再利用导数的几何意义即可求解.
【详解】
因为,
所以,则曲线在点处的切线斜率为,
故所求切线的倾斜角为.
故选:C
2.D
【分析】
由导数的定义可得,即可得答案.
【详解】
根据题意,,
故.
故选:D.
【点睛】
本题考查导数的定义,属于基础题.
3.A
【分析】
根据导数的几何意义,结合图象判断.
【详解】
根据题意,点A(x1,f(x1)),B(x2,f(x2),为f(x)的导函数,
则为点A处切线的斜率,设其斜率为k1,为点B处切线的斜率,设其斜率为k2,
由函数的图象可得k1>k2,即有;
故选:A.
4.D
【分析】
根据导数的概念,直接计算,即可得出结果.
【详解】
由题意,根据导数的概念可得,
,
所以.
故选:D.
5.C
【分析】
由瞬时变化率的物理意义判断.
【详解】
是物体在这一时刻的瞬时速度.
故选:C.
6.C
【分析】
,利用导数的定义即可求解.
【详解】
,
故选:C.
7.B
【分析】
由已知结合导数的定义即可直接求解.
【详解】
解:因为函数在处的导数为1,
则.
故选:B.
【点睛】
本题考查导数的概念,涉及极限的性质,属于基础题.
8.B
【分析】
根据瞬时速度与导数的关系,先对求导,再把代入进行运算即可
【详解】
解:由,得,
当时,,
所以高台跳水运动中运动员在时的瞬时速度,
故选:B
【点睛】
此题考查导数的定义与运算,考查运算能力,属于基础题
9.D
【分析】
由导数的几何意义即可求解.
【详解】
解:的几何意义是函数的图象在点处的切线的斜率.
故选:D.
10.B
【分析】
利用导数的几何意义即可求解.
【详解】
由图可知:,
即.
故选:B
【点睛】
本题考查了导数的几何意义,考查了数形结合的思想,属于基础题.
11.A
【分析】
由切线经过坐标轴上的两点求出切线的斜率和切线方程,然后求出,即可得到的值.
【详解】
解:因为切线过和,所以,
所以切线方程为,取,则,所以,
所以.
故选:A.
【点睛】
本题考查了导数的几何意义,考查了数形结合思想,属基础题.
12.A
【分析】
由条件可得,
【详解】
因为函数的图象在点P处的切线方程是
所以,
所以4
故选:A
【点睛】
本题考查的是导数的几何意义,较简单.
13.
【分析】
根据极限的运算法则,直接计算,即可得出结果.
【详解】
.
故答案为:.
14.
【分析】
首先根据极限的运算法则,对所给的极限进行整理,写成符合导数的定义的形式,写出导数的值,即可得到函数在这一个点处的切线的斜率
【详解】
解:因为,
所以,所以,
所以,
所以曲线在点处的切线的斜率为,
故答案为:
【点睛】
此题考查导数的定义,切线的斜率,以及极限的运算,属于基础题
15.6
【分析】
根据导数的定义,将所求的式子用表示,即可求解.
【详解】
.
故答案为:6.
【点睛】
本题考查利用导数的定义求值,要注意函数值的变化量和自变量的变化量要一致,属于容易题.
16.函数在处的导数为.
【分析】
由导数的定义利用极限的运算可得.
【详解】
∵ ,
∴,故.
【点睛】
本题考查定义法求导数的值,涉及极限的运算,属基础题.
A级 巩固基础
一、单选题
1.设,则曲线在点处的切线的倾斜角是( )
A. B. C. D.
2.设是可导函数,且,则( )
A.2 B. C.1 D.
3.如图,点A(x1,f(x1)),B(x2,f(x2))在函数f(x)的图象上,且x2<x1,为f(x)的导函数,则与的大小关系是( )
A. B.
C. D.不能确定
4.若(m为常数),则等于( )
A. B.1 C.m D.
5.某物体的运动方程为(位移单位:m,时间单位:s),若,则下列说法中正确的是( )
A.是物体从开始到这段时间内的平均速度
B.是物体从到这段时间内的速度
C.是物体在这一时刻的瞬时速度
D.是物体从到这段时间内的平均速度
6.已知函数在处的导数为1,则 ( )
A. B. C. D.
7.已知函数在处的导数为1,则( )
A.0 B. C.1 D.2
8.在高台跳水运动中时运动员相对于水面的高度(单位:)是,则高台跳水运动中运动员在时的瞬时速度是( )
A. B. C.13.1 D.3.3
B级 综合应用
9.函数在处的导数的几何意义是( )
A.在点处与的图象只有一个交点的直线的斜率
B.过点的切线的斜率
C.点与点的连线的斜率
D.函数的图象在点处的切线的斜率
10.已知函数f(x)的图象如图所示,下列数值的排序正确的是( )
A. B.
C. D.
11.函数在处的切线如图所示,则( )
A.0 B. C. D.
12.如图,函数的图象在点P处的切线方程是,则( )
A.4 B.3 C. D.
二、填空题
13.___________
14.设为可导函数,且满足,则曲线在点处的切线的斜率是______.
15.已知,则______.
C级 拓展探究
三、解答题
16.根据导数的定义求函数在处的导数.
参考答案
1.C
【分析】
根据导数的概念可得,再利用导数的几何意义即可求解.
【详解】
因为,
所以,则曲线在点处的切线斜率为,
故所求切线的倾斜角为.
故选:C
2.D
【分析】
由导数的定义可得,即可得答案.
【详解】
根据题意,,
故.
故选:D.
【点睛】
本题考查导数的定义,属于基础题.
3.A
【分析】
根据导数的几何意义,结合图象判断.
【详解】
根据题意,点A(x1,f(x1)),B(x2,f(x2),为f(x)的导函数,
则为点A处切线的斜率,设其斜率为k1,为点B处切线的斜率,设其斜率为k2,
由函数的图象可得k1>k2,即有;
故选:A.
4.D
【分析】
根据导数的概念,直接计算,即可得出结果.
【详解】
由题意,根据导数的概念可得,
,
所以.
故选:D.
5.C
【分析】
由瞬时变化率的物理意义判断.
【详解】
是物体在这一时刻的瞬时速度.
故选:C.
6.C
【分析】
,利用导数的定义即可求解.
【详解】
,
故选:C.
7.B
【分析】
由已知结合导数的定义即可直接求解.
【详解】
解:因为函数在处的导数为1,
则.
故选:B.
【点睛】
本题考查导数的概念,涉及极限的性质,属于基础题.
8.B
【分析】
根据瞬时速度与导数的关系,先对求导,再把代入进行运算即可
【详解】
解:由,得,
当时,,
所以高台跳水运动中运动员在时的瞬时速度,
故选:B
【点睛】
此题考查导数的定义与运算,考查运算能力,属于基础题
9.D
【分析】
由导数的几何意义即可求解.
【详解】
解:的几何意义是函数的图象在点处的切线的斜率.
故选:D.
10.B
【分析】
利用导数的几何意义即可求解.
【详解】
由图可知:,
即.
故选:B
【点睛】
本题考查了导数的几何意义,考查了数形结合的思想,属于基础题.
11.A
【分析】
由切线经过坐标轴上的两点求出切线的斜率和切线方程,然后求出,即可得到的值.
【详解】
解:因为切线过和,所以,
所以切线方程为,取,则,所以,
所以.
故选:A.
【点睛】
本题考查了导数的几何意义,考查了数形结合思想,属基础题.
12.A
【分析】
由条件可得,
【详解】
因为函数的图象在点P处的切线方程是
所以,
所以4
故选:A
【点睛】
本题考查的是导数的几何意义,较简单.
13.
【分析】
根据极限的运算法则,直接计算,即可得出结果.
【详解】
.
故答案为:.
14.
【分析】
首先根据极限的运算法则,对所给的极限进行整理,写成符合导数的定义的形式,写出导数的值,即可得到函数在这一个点处的切线的斜率
【详解】
解:因为,
所以,所以,
所以,
所以曲线在点处的切线的斜率为,
故答案为:
【点睛】
此题考查导数的定义,切线的斜率,以及极限的运算,属于基础题
15.6
【分析】
根据导数的定义,将所求的式子用表示,即可求解.
【详解】
.
故答案为:6.
【点睛】
本题考查利用导数的定义求值,要注意函数值的变化量和自变量的变化量要一致,属于容易题.
16.函数在处的导数为.
【分析】
由导数的定义利用极限的运算可得.
【详解】
∵ ,
∴,故.
【点睛】
本题考查定义法求导数的值,涉及极限的运算,属基础题.
