8.4.1平面-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课前检测(Word含解析)
文档属性
| 名称 | 8.4.1平面-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课前检测(Word含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 622.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 00:00:00 | ||
图片预览





文档简介
人教A版8.4.1平面课前检测题
一、单选题
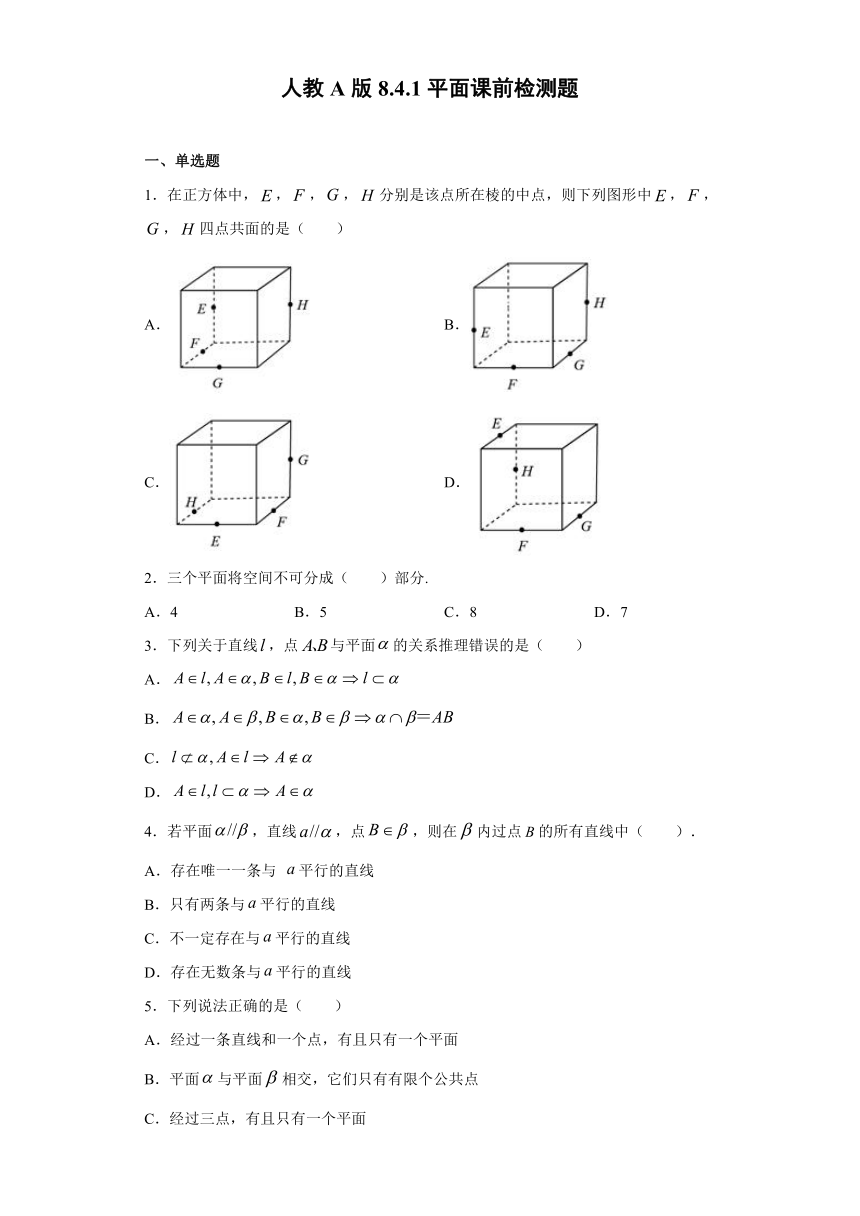
1.在正方体中,,,,分别是该点所在棱的中点,则下列图形中,,,四点共面的是( )
A. B.
C. D.
2.三个平面将空间不可分成( )部分.
A.4 B.5 C.8 D.7
3.下列关于直线,点与平面的关系推理错误的是( )
A.
B.
C.
D.
4.若平面,直线,点,则在内过点的所有直线中( ).
A.存在唯一一条与 平行的直线
B.只有两条与平行的直线
C.不一定存在与平行的直线
D.存在无数条与平行的直线
5.下列说法正确的是( )
A.经过一条直线和一个点,有且只有一个平面
B.平面与平面相交,它们只有有限个公共点
C.经过三点,有且只有一个平面
D.如果两个平面有三个不共线的公共点,那么这两个平面重合
6.下列说法正确的是( )
A.棱柱的侧面可以是三角形
B.用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台
C.过空间内三点,有且只有一个平面
D.四面体的任何一个面都可以作为棱锥的底面
7.如图所示,用符号语言可表达为( )
A., B.,
C., D.,
8.两个平面若有三个公共点,则这两个平面( )
A.相交 B.重合
C.相交或重合 D.以上都不对
9.如图所示的是平行四边形所在的平面,有下列表示方法:①平面;②平面;③平面;④平面;⑤;⑥平面.其中不正确的是( )
A.④⑤ B.③④⑤ C.②③④⑤ D.③⑤
10.已知下列四个结论:①铺得很平的一张白纸是一个平面;②平面的形状是平行四边形;③一个平面的面积可以等于.其中正确结论的个数是( )
A. B. C. D.
11.下列叙述错误的是( )
A.若p∈α∩β,且α∩β=l,则p∈l.
B.若直线a∩b=A,则直线a与b能确定一个平面.
C.三点A,B,C确定一个平面.
D.若A∈l,B∈l且A∈α,B∈α则lα.
12.给出下列四个命题,其中正确的是( )
①空间四点共面,则其中必有三点共线;②空间四点不共面,则其中任何三点不共线;③空间四点中存在三点共线,则此四点共面;④空间四点中任何三点不共线
A.②③ B.①②③ C.①② D.②③④
13.下面四个条件中,能确定一个平面的是( )
A.空间中任意三点 B.空间中两条直线
C.空间中两条相交直线 D.一条直线和一个点
14.四个顶点不在同一平面上的四边形中,,,,分别是边,,,上的点,如果直线,交于点,那么( )
A.点一定在直线上
B.点一定在直线上
C.点一定在平面外
D.点一定在平面内
二、解答题
15.三个平面分空间有几种情况?并说明每种情况下能将空间分成几部分.
参考答案
1.B
【分析】
选项A、B、C中,由其中三个点确定一个平面,再判断第四个点是否在该平面内,选项B通过证明两直线平行,从而判断四点共面.
【详解】
选项A,点,,确定一个平面,该平面与底面交于,
而点不在直线上,故,,,不共面,
选项A错误;
选项B,连接底面对角线,
则由中位线定理可知,,
又易知,则,
故,,,共面,选项B正确;
选项C,显然,,所确定的平面为正方体的底面,
而点不在该平面内,故故,,,不共面,
选项C错误;
选项D,如图,取部分棱的中点,顺次连接,可得一正六边形,
也即是点,,确定的平面与正方体正面的交线为,
而点不在直线上,故,,,四点不共面,
选项D错误.
【点睛】
方法点睛:判断四点共线的方法有:
(1)四点中两点连线所成的两条直线平行、相交或重合;
(2)由其中三点确定一个平面,再证明第四点在这个平面内;
(3)若其中三点共线,则此四点一定共面.
2.B
【分析】
根据三个平面的不同位置关系找出把空间分成的部分,即可得出结论.
【详解】
若三个平面互相平行,则把空间分成4部分;若两个平面互相平行,另一平面与它们相交,则把空间分成6部分;三个平面两两相交,且有一条交线,则把空间分成6部分;三个平面两两相交,且有三条交线,则把空间分成7或8部分.
故选:B.
3.C
【分析】
由平面的性质:公理1,可判断A;
由平面的性质:公理2,可判断B;
由线面的位置关系可判断CD.
【详解】
A、B分别是公理1、2的符号表示,故它们都是正确的;
对于C,有两种可能, 或与 相交;若交点为,则且.故错;
D是直线在平面内的定义,正确,
故选C.
【点睛】
本题主要考查了平面的基本性质及推论,属于基础题,亦属于易错题.利用集合的符号语言来描述平面几何中点、线、面的位置关系,学生在理解上存在着差异,点相当于元素,而线与平面看成是点的集合,所以点与线面的关系是属不属于的关系,而直线与平面之间是含与不含的关系,线与面之间当然也可以进行交运算.
4.C
【分析】
讨论、、三种情况下,在内过点是否存在直线与平行即可知正确选项.
【详解】
平面,直线,点,
1、当时,在内过点有且仅有一条直线与平行;
2、当时,在内过点有且仅有一条直线与平行;
3、当时,在内过点不存在直线与平行;
故选:C
5.D
【分析】
对于,当点在直线上时,说法不正确;对于,它们无数个公共点,说法不正确;对于,要求三点不共线,说法不正确;对于,说法正确.
【详解】
对于,当点在直线上时,说法不正确;
对于,当平面与平面相交,它们无数个公共点,这些公共点在一条公共直线上,说法不正确;
对于,经过不在一条直线上的三点,有且只有一个平面,说法不正确;
对于,如果两个平面有三个不共线的公共点,那么这两个平面重合,说法正确.
故选:D
【点睛】
关键点点睛:掌握平面的基本性质是解题关键.
6.D
【分析】
根据棱柱、棱柱和棱台的结构特征和平面的性质可判断.
【详解】
对A,棱柱的侧面是平行四边形,故A错误;
对B,用一个平行于底面的平面去截棱锥,棱锥底面和截面之间的部分是棱台,故B错误;
对C,过不在一条直线上的三点,有且只有一个平面,故C错误;
对D,因为四面体的每一个面都是三角形,故任何一个面都可以作为棱锥的底面,故D正确.
故选:D.
7.A
【分析】
根据课本点、线、面及其关系的符号表示规定逐一判断.
【详解】
点为元素,线和面是集合,根据点与集合、集合与集合之间的关系易得.
故选:A
8.C
【分析】
根据平面的基本性质判断.
【详解】
两个平面若有三个公共点,当这三个点不共线时,两平面重合,当这三个点共线时,这两个平面相交或重合.
故选:C.
【点睛】
本题考查平面的基本性质,平面的基本性质公理3中一定要注意三点不共线才能确定一个平面,属于基础题.
9.D
【分析】
根据平面的表示方法判断.
【详解】
③中不为对角线,故错误;⑤中漏掉“平面”两字,故错误.
故选:D.
10.A
【分析】
根据平面的特性和平面的画法判断.
【详解】
在立体几何中,平面是无限延展的,故①③错误;
通常我们画一个平行四边形来表示一个平面,但并不是说平面就是平行四边形,故②错误,
故选:A.
11.C
【分析】
由空间线面位置关系,结合公理即推论,逐个验证即可.
【详解】
选项,点在是两平面的公共点,当然在交线上,故正确;
选项,由公理的推论可知,两相交直线确定一个平面,故正确;
选项,只有不共线的三点才能确定一个平面,故错误;
选项,由公理1,直线上有两点在一个平面内,则整条直线都在平面内.
故选:C
12.A
【分析】
取及其内部一点(不包括边界),可判断①的正误;取三棱锥的四个顶点,可判断②的正误;利用空间中的公理可判断③的正误;由、、、四点共线可判断④的正误.综合可得出结论.
【详解】
对于命题①,如下图所示:
点为内一点,则、、、四点共面,但这四点中无任何三点共线,①错误;
对于命题②,空间四点不共面,如三棱锥的四个顶点,、、、四点中无任何三点共线,②正确;
对于命题③,如果、、三点共线,且,则这四点共面;
如果、、三点共线,且,则过点与直线有且只有一个平面.
所以,③正确;
对于命题④,取及的中点,则、、共线,④错误.
故选:A.
【点睛】
本题考查空间点共面与点共线的判断,属于基础题.
13.C
【分析】
根据每个选项,可举出相应的反例进而得到结果.
【详解】
A,空间任意三点,当三点共线时能确定一条直线而不是平面,故不正确;
B. 空间两条直线,当两条直线重合时,过这条直线的平面有无数个,故不正确;
C. 空间两条平行直线,根据课本中的判定得到是正确的;
D. 一条直线和一个点,当这个点在直线上时,过这条直线的平面有无数个,故不正确.
故选:C.
14.A
【分析】
由两个面的交点在两个面的交线上,知P在两面的交线上,由AC是两平面的交线,知点P必在直线AC上.
【详解】
解:∵EF在面ABC内,而GH在面ADC内,
且EF和GH能相交于点P,
∴P在面ABC和面ADC的交线上,
∵AC是两平面的交线,
所以点P必在直线AC上.
故选:A.
【点睛】
本题考查平面的基本性质及其推论,是基础题.解题时要认真审题,仔细解答.
15.答案见解析.
【分析】
按照平面的位置关系分类,即可得解.
【详解】
三个平面分空间有种情况,
若三个平面均平行,则将空间分成部分;
若三个平面交于一条线,则将空间分成部分;
若三个平面两两相交,且交线不平行时,则将空间分成部分;
若三个平面两两相交,且交线平行时,则将空间分成部分.
一、单选题
1.在正方体中,,,,分别是该点所在棱的中点,则下列图形中,,,四点共面的是( )
A. B.
C. D.
2.三个平面将空间不可分成( )部分.
A.4 B.5 C.8 D.7
3.下列关于直线,点与平面的关系推理错误的是( )
A.
B.
C.
D.
4.若平面,直线,点,则在内过点的所有直线中( ).
A.存在唯一一条与 平行的直线
B.只有两条与平行的直线
C.不一定存在与平行的直线
D.存在无数条与平行的直线
5.下列说法正确的是( )
A.经过一条直线和一个点,有且只有一个平面
B.平面与平面相交,它们只有有限个公共点
C.经过三点,有且只有一个平面
D.如果两个平面有三个不共线的公共点,那么这两个平面重合
6.下列说法正确的是( )
A.棱柱的侧面可以是三角形
B.用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台
C.过空间内三点,有且只有一个平面
D.四面体的任何一个面都可以作为棱锥的底面
7.如图所示,用符号语言可表达为( )
A., B.,
C., D.,
8.两个平面若有三个公共点,则这两个平面( )
A.相交 B.重合
C.相交或重合 D.以上都不对
9.如图所示的是平行四边形所在的平面,有下列表示方法:①平面;②平面;③平面;④平面;⑤;⑥平面.其中不正确的是( )
A.④⑤ B.③④⑤ C.②③④⑤ D.③⑤
10.已知下列四个结论:①铺得很平的一张白纸是一个平面;②平面的形状是平行四边形;③一个平面的面积可以等于.其中正确结论的个数是( )
A. B. C. D.
11.下列叙述错误的是( )
A.若p∈α∩β,且α∩β=l,则p∈l.
B.若直线a∩b=A,则直线a与b能确定一个平面.
C.三点A,B,C确定一个平面.
D.若A∈l,B∈l且A∈α,B∈α则lα.
12.给出下列四个命题,其中正确的是( )
①空间四点共面,则其中必有三点共线;②空间四点不共面,则其中任何三点不共线;③空间四点中存在三点共线,则此四点共面;④空间四点中任何三点不共线
A.②③ B.①②③ C.①② D.②③④
13.下面四个条件中,能确定一个平面的是( )
A.空间中任意三点 B.空间中两条直线
C.空间中两条相交直线 D.一条直线和一个点
14.四个顶点不在同一平面上的四边形中,,,,分别是边,,,上的点,如果直线,交于点,那么( )
A.点一定在直线上
B.点一定在直线上
C.点一定在平面外
D.点一定在平面内
二、解答题
15.三个平面分空间有几种情况?并说明每种情况下能将空间分成几部分.
参考答案
1.B
【分析】
选项A、B、C中,由其中三个点确定一个平面,再判断第四个点是否在该平面内,选项B通过证明两直线平行,从而判断四点共面.
【详解】
选项A,点,,确定一个平面,该平面与底面交于,
而点不在直线上,故,,,不共面,
选项A错误;
选项B,连接底面对角线,
则由中位线定理可知,,
又易知,则,
故,,,共面,选项B正确;
选项C,显然,,所确定的平面为正方体的底面,
而点不在该平面内,故故,,,不共面,
选项C错误;
选项D,如图,取部分棱的中点,顺次连接,可得一正六边形,
也即是点,,确定的平面与正方体正面的交线为,
而点不在直线上,故,,,四点不共面,
选项D错误.
【点睛】
方法点睛:判断四点共线的方法有:
(1)四点中两点连线所成的两条直线平行、相交或重合;
(2)由其中三点确定一个平面,再证明第四点在这个平面内;
(3)若其中三点共线,则此四点一定共面.
2.B
【分析】
根据三个平面的不同位置关系找出把空间分成的部分,即可得出结论.
【详解】
若三个平面互相平行,则把空间分成4部分;若两个平面互相平行,另一平面与它们相交,则把空间分成6部分;三个平面两两相交,且有一条交线,则把空间分成6部分;三个平面两两相交,且有三条交线,则把空间分成7或8部分.
故选:B.
3.C
【分析】
由平面的性质:公理1,可判断A;
由平面的性质:公理2,可判断B;
由线面的位置关系可判断CD.
【详解】
A、B分别是公理1、2的符号表示,故它们都是正确的;
对于C,有两种可能, 或与 相交;若交点为,则且.故错;
D是直线在平面内的定义,正确,
故选C.
【点睛】
本题主要考查了平面的基本性质及推论,属于基础题,亦属于易错题.利用集合的符号语言来描述平面几何中点、线、面的位置关系,学生在理解上存在着差异,点相当于元素,而线与平面看成是点的集合,所以点与线面的关系是属不属于的关系,而直线与平面之间是含与不含的关系,线与面之间当然也可以进行交运算.
4.C
【分析】
讨论、、三种情况下,在内过点是否存在直线与平行即可知正确选项.
【详解】
平面,直线,点,
1、当时,在内过点有且仅有一条直线与平行;
2、当时,在内过点有且仅有一条直线与平行;
3、当时,在内过点不存在直线与平行;
故选:C
5.D
【分析】
对于,当点在直线上时,说法不正确;对于,它们无数个公共点,说法不正确;对于,要求三点不共线,说法不正确;对于,说法正确.
【详解】
对于,当点在直线上时,说法不正确;
对于,当平面与平面相交,它们无数个公共点,这些公共点在一条公共直线上,说法不正确;
对于,经过不在一条直线上的三点,有且只有一个平面,说法不正确;
对于,如果两个平面有三个不共线的公共点,那么这两个平面重合,说法正确.
故选:D
【点睛】
关键点点睛:掌握平面的基本性质是解题关键.
6.D
【分析】
根据棱柱、棱柱和棱台的结构特征和平面的性质可判断.
【详解】
对A,棱柱的侧面是平行四边形,故A错误;
对B,用一个平行于底面的平面去截棱锥,棱锥底面和截面之间的部分是棱台,故B错误;
对C,过不在一条直线上的三点,有且只有一个平面,故C错误;
对D,因为四面体的每一个面都是三角形,故任何一个面都可以作为棱锥的底面,故D正确.
故选:D.
7.A
【分析】
根据课本点、线、面及其关系的符号表示规定逐一判断.
【详解】
点为元素,线和面是集合,根据点与集合、集合与集合之间的关系易得.
故选:A
8.C
【分析】
根据平面的基本性质判断.
【详解】
两个平面若有三个公共点,当这三个点不共线时,两平面重合,当这三个点共线时,这两个平面相交或重合.
故选:C.
【点睛】
本题考查平面的基本性质,平面的基本性质公理3中一定要注意三点不共线才能确定一个平面,属于基础题.
9.D
【分析】
根据平面的表示方法判断.
【详解】
③中不为对角线,故错误;⑤中漏掉“平面”两字,故错误.
故选:D.
10.A
【分析】
根据平面的特性和平面的画法判断.
【详解】
在立体几何中,平面是无限延展的,故①③错误;
通常我们画一个平行四边形来表示一个平面,但并不是说平面就是平行四边形,故②错误,
故选:A.
11.C
【分析】
由空间线面位置关系,结合公理即推论,逐个验证即可.
【详解】
选项,点在是两平面的公共点,当然在交线上,故正确;
选项,由公理的推论可知,两相交直线确定一个平面,故正确;
选项,只有不共线的三点才能确定一个平面,故错误;
选项,由公理1,直线上有两点在一个平面内,则整条直线都在平面内.
故选:C
12.A
【分析】
取及其内部一点(不包括边界),可判断①的正误;取三棱锥的四个顶点,可判断②的正误;利用空间中的公理可判断③的正误;由、、、四点共线可判断④的正误.综合可得出结论.
【详解】
对于命题①,如下图所示:
点为内一点,则、、、四点共面,但这四点中无任何三点共线,①错误;
对于命题②,空间四点不共面,如三棱锥的四个顶点,、、、四点中无任何三点共线,②正确;
对于命题③,如果、、三点共线,且,则这四点共面;
如果、、三点共线,且,则过点与直线有且只有一个平面.
所以,③正确;
对于命题④,取及的中点,则、、共线,④错误.
故选:A.
【点睛】
本题考查空间点共面与点共线的判断,属于基础题.
13.C
【分析】
根据每个选项,可举出相应的反例进而得到结果.
【详解】
A,空间任意三点,当三点共线时能确定一条直线而不是平面,故不正确;
B. 空间两条直线,当两条直线重合时,过这条直线的平面有无数个,故不正确;
C. 空间两条平行直线,根据课本中的判定得到是正确的;
D. 一条直线和一个点,当这个点在直线上时,过这条直线的平面有无数个,故不正确.
故选:C.
14.A
【分析】
由两个面的交点在两个面的交线上,知P在两面的交线上,由AC是两平面的交线,知点P必在直线AC上.
【详解】
解:∵EF在面ABC内,而GH在面ADC内,
且EF和GH能相交于点P,
∴P在面ABC和面ADC的交线上,
∵AC是两平面的交线,
所以点P必在直线AC上.
故选:A.
【点睛】
本题考查平面的基本性质及其推论,是基础题.解题时要认真审题,仔细解答.
15.答案见解析.
【分析】
按照平面的位置关系分类,即可得解.
【详解】
三个平面分空间有种情况,
若三个平面均平行,则将空间分成部分;
若三个平面交于一条线,则将空间分成部分;
若三个平面两两相交,且交线不平行时,则将空间分成部分;
若三个平面两两相交,且交线平行时,则将空间分成部分.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
