华师大版九年级下册数学知识点总结
图片预览




文档简介
华师大版九年级下册数学知识点总结
第二十六章 二次函数
一、二次函数概念:
1、二次函数的概念:一般地,形如(是常数,)的函数,叫做二次函数。
这里需要强调:和一元二次方程类似,二次项系数,而可以为零。二次函数的定义域是全体实数。
2、二次函数的结构特征:
⑴ 等号左边是函数,右边是关于自变量的二次式,的最高次数是2。
⑵ 是常数,是二次项系数,是一次项系数,是常数项。
二、二次函数的基本形式
1. 二次函数基本形式:的性质:a 的绝对值越大,抛物线的开口越小。
的符号 开口方向 顶点坐标 对称轴 性质
向上
轴 时,随的增大而增大;
时,随的增大而减小;
时,有最小值。
向下
轴 时,随的增大而减小;
时,随的增大而增大;
时,有最大值。
2. 的性质:
的符号 开口方向 顶点坐标 对称轴 性质
向上
轴 时,随的增大而增大;
时,随的增大而减小;
时,有最小值。
向下
轴 时,随的增大而减小;
时,随的增大而增大;
时,有最大值。
3. 的性质:
的符号 开口方向 顶点坐标 对称轴 性质
向上
X=h 时,随的增大而增大;
时,随的增大而减小;
时,有最小值。
向下
X=h 时,随的增大而减小;
时,随的增大而增大;
时,有最大值。
4. 的性质:
的符号 开口方向 顶点坐标 对称轴 性质
向上
X=h 时,随的增大而增大;时,随的增大而减小;时,有最小值。
向下
X=h 时,随的增大而减小;时,随的增大而增大;时,有最大值。
三、二次函数图象的平移
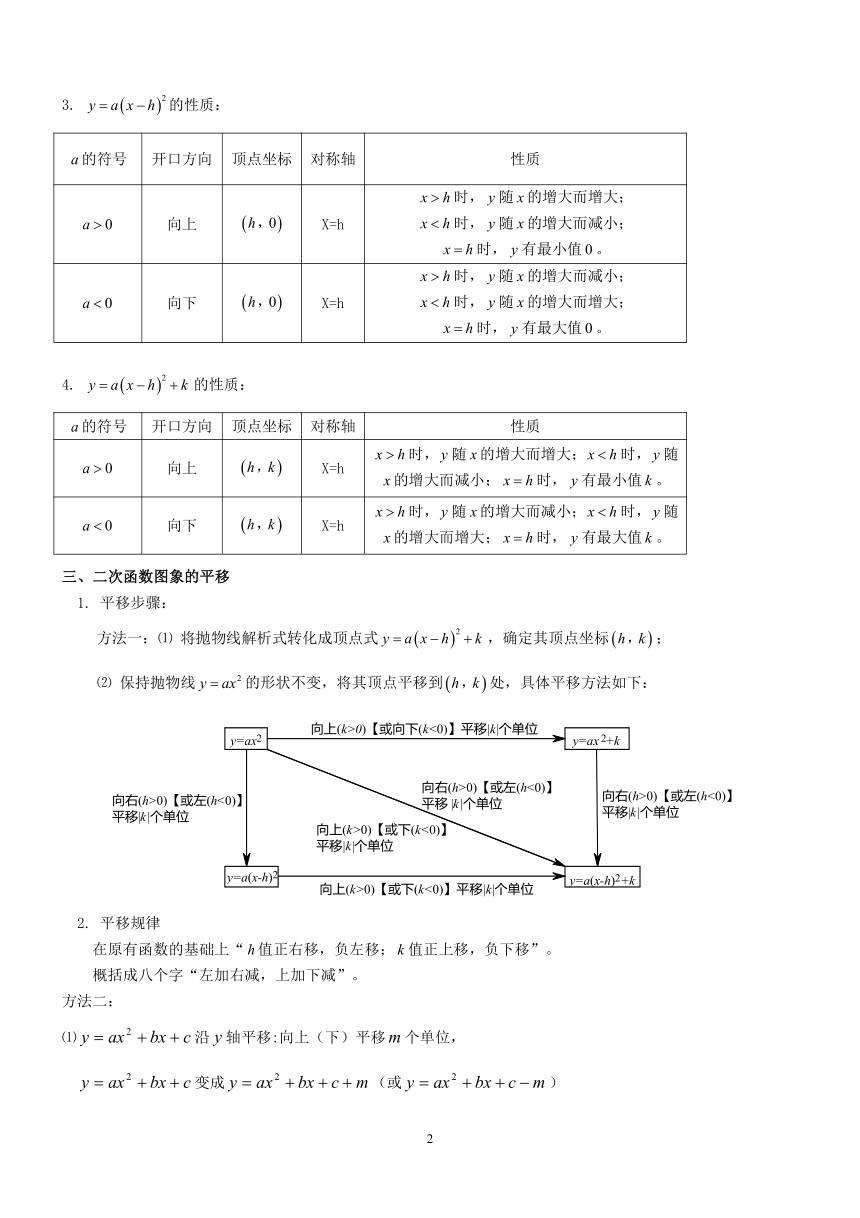
1. 平移步骤:
方法一:⑴ 将抛物线解析式转化成顶点式,确定其顶点坐标;
⑵ 保持抛物线的形状不变,将其顶点平移到处,具体平移方法如下:
2. 平移规律
在原有函数的基础上“值正右移,负左移;值正上移,负下移”。
概括成八个字“左加右减,上加下减”。
方法二:
⑴沿轴平移:向上(下)平移个单位,
变成(或)
⑵沿轴平移:向左(右)平移个单位,
变成(或)
四、二次函数与的比较
从解析式上看,与是两种不同的表达形式,后者通过配方可以得到前者,即,其中。
五、二次函数图象的画法
五点绘图法:利用配方法将二次函数化为顶点式,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:顶点、与轴的交点、以及关于对称轴对称的点、与轴的交点,(若与轴没有交点,则取两组关于对称轴对称的点).
画草图时应抓住以下几点:开口方向,对称轴,顶点,与轴的交点,与轴的交点.
六、二次函数的性质
1. 当时,抛物线开口向上,对称轴为,顶点坐标为。
当时,随的增大而减小;当时,随的增大而增大;当时,有最小值。
2. 当时,抛物线开口向下,对称轴为,顶点坐标为。当时,随的增大而增大;当时,随的增大而减小;当时,有最大值。
七、二次函数解析式的表示方法
1. 一般式:(,,为常数,);
2. 顶点式:(,,为常数,);
3. 两根式:(,,是抛物线与轴两交点的横坐标).
注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线与轴有交点,即时,抛物线的解析式才可以用交点式表示。二次函数解析式的这三种形式可以互化.
八、二次函数的图象与各项系数之间的关系
1. 二次项系数
二次函数中,作为二次项系数,显然。
⑴ 当时,抛物线开口向上,的值越大,开口越小,反之的值越小,开口越大;
⑵ 当时,抛物线开口向下,的值越小,开口越小,反之的值越大,开口越大。
总结起来,决定了抛物线开口的大小和方向,的正负决定开口方向,的大小决定开口的大小。
2. 一次项系数
在二次项系数确定的前提下,决定了抛物线的对称轴。
⑴ 在的前提下,
当时,,即抛物线的对称轴在轴左侧;
当时,,即抛物线的对称轴就是轴;
当时,,即抛物线对称轴在轴的右侧。
⑵ 在的前提下,结论刚好与上述相反,即
当时,,即抛物线的对称轴在轴右侧;
当时,,即抛物线的对称轴就是轴;
当时,,即抛物线对称轴在轴的左侧。
总结起来,在确定的前提下,决定了抛物线对称轴的位置。
的符号的判定:对称轴在轴左边则,在轴的右侧则,概括的说就是“左同右异”
总结:
3. 常数项
⑴ 当时,抛物线与轴的交点在轴上方,即抛物线与轴交点的纵坐标为正;
⑵ 当时,抛物线与轴的交点为坐标原点,即抛物线与轴交点的纵坐标为;
⑶ 当时,抛物线与轴的交点在轴下方,即抛物线与轴交点的纵坐标为负。
总结起来,决定了抛物线与轴交点的位置。
总之,只要都确定,那么这条抛物线就是唯一确定的。
二次函数解析式的确定:
根据已知条件确定二次函数解析式,通常利用待定系数法。用待定系数法求二次函数的解析式必须根据题目的特点,选择适当的形式,才能使解题简便。一般来说,有如下几种情况:
1. 已知抛物线上三点的坐标,一般选用一般式;
2. 已知抛物线顶点或对称轴或最大(小)值,一般选用顶点式;
3. 已知抛物线与轴的两个交点的横坐标,一般选用两根式;
4. 已知抛物线上纵坐标相同的两点,常选用顶点式。
九、二次函数图象的对称
二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达
1. 关于轴对称
关于轴对称后,得到的解析式是;
关于轴对称后,得到的解析式是;
2. 关于轴对称
关于轴对称后,得到的解析式是;
关于轴对称后,得到的解析式是;
3. 关于原点对称
关于原点对称后,得到的解析式是;
关于原点对称后,得到的解析式是;
4. 关于顶点对称(即:抛物线绕顶点旋转180°)
关于顶点对称后,得到的解析式是;
关于顶点对称后,得到的解析式是。
5. 关于点对称
关于点对称后,得到的解析式是
根据对称的性质,显然无论作何种对称变换,抛物线的形状一定不会发生变化,因此永远不变。求抛物线的对称抛物线的表达式时,可以依据题意或方便运算的原则,选择合适的形式,习惯上是先确定原抛物线(或表达式已知的抛物线)的顶点坐标及开口方向,再确定其对称抛物线的顶点坐标及开口方向,然后再写出其对称抛物线的表达式。
十、二次函数与一元二次方程:
1. 二次函数与一元二次方程的关系(二次函数与轴交点情况):
一元二次方程是二次函数当函数值时的特殊情况.
图象与轴的交点个数:
① 当时,图象与轴交于两点,其中的是一元二次方程的两根。这两点间的距离.
② 当时,图象与轴只有一个交点;
③ 当时,图象与轴没有交点.
当时,图象落在轴的上方,无论为任何实数,都有;
当时,图象落在轴的下方,无论为任何实数,都有。
2. 抛物线的图象与轴一定相交,交点坐标为,;
3. 二次函数常用解题方法总结:
⑴ 求二次函数的图象与轴的交点坐标,需转化为一元二次方程;
⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式;
⑶ 根据图象的位置判断二次函数中,,的符号,或由二次函数中,,的符号判断图象的位置,要数形结合;
⑷ 二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与轴的一个交点坐标,可由对称性求出另一个交点坐标.
⑸ 与二次函数有关的还有二次三项式,二次三项式本身就是所含字母的二次函数;下面以时为例,揭示二次函数、二次三项式和一元二次方程之间的内在联系:
抛物线与轴有两个交点 二次三项式的值可正、可零、可负 一元二次方程有两个不相等实根
抛物线与轴只有一个交点 二次三项式的值为非负 一元二次方程有两个相等的实数根
抛物线与轴无交点 二次三项式的值恒为正 一元二次方程无实数根.
二次函数图像参考:
十一、函数的应用
二次函数应用
第二十七章:《圆》
一、知识回顾
圆的周长: C=2πr或C=πd、圆的面积:S=πr?
圆环面积计算方法:S=πR?-πr?或S=π(R?-r?)(R是大圆半径,r是小圆半径)
二、知识要点
一、圆的概念
集合形式的概念: 1、 圆可以看作是到定点的距离等于定长的点的集合;
2、圆的外部:可以看作是到定点的距离大于定长的点的集合;
3、圆的内部:可以看作是到定点的距离小于定长的点的集合
轨迹形式的概念:
1、圆:到定点的距离等于定长的点的轨迹就是以定点为圆心,定长为半径的圆;
固定的端点O为圆心。连接圆上任意两点的线段叫做弦,经过圆心的弦叫直径。圆上任意两点之间的部分叫做圆弧,简称弧。
2、垂直平分线:到线段两端距离相等的点的轨迹是这条线段的垂直平分线;
3、角的平分线:到角两边距离相等的点的轨迹是这个角的平分线;
4、到直线的距离相等的点的轨迹是:平行于这条直线且到这条直线的距离等于定长的两条直线;
5、到两条平行线距离相等的点的轨迹是:平行于这两条平行线且到两条直线距离都相等的一条直线。
二、点与圆的位置关系
1、点在圆内 点在圆内;
2、点在圆上 点在圆上;
3、点在圆外 点在圆外;
三、直线与圆的位置关系
1、直线与圆相离 无交点;
2、直线与圆相切 有一个交点;
3、直线与圆相交 有两个交点;
四、圆与圆的位置关系
外离(图1) 无交点 ;
外切(图2) 有一个交点 ;
相交(图3) 有两个交点 ;
内切(图4) 有一个交点 ;
内含(图5) 无交点 ;
五、垂径定理
垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。
推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;
(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧
以上共4个定理,简称2推3定理:此定理中共5个结论中,只要知道其中2个即可推出其它3个结论,即:
①是直径 ② ③ ④ 弧弧 ⑤ 弧弧
中任意2个条件推出其他3个结论。
推论2:圆的两条平行弦所夹的弧相等。
即:在⊙中,∵∥
∴弧弧
六、圆心角定理
顶点到圆心的角,叫圆心角。
圆心角定理:同圆或等圆中,相等的圆心角所对的弦相等,所对的弧相等,弦心距相等。 此定理也称1推3定理,即上述四个结论中,
只要知道其中的1个相等,则可以推出其它的3个结论,
即:①;②;
③;④ 弧弧
七、圆周角定理
顶点在圆上,并且两边都与圆相交的角,叫圆周角。
1、圆周角定理:同弧所对的圆周角等于它所对的圆心的角的一半。
即:∵和是弧所对的圆心角和圆周角
∴
2、圆周角定理的推论:
推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧是等弧;
即:在⊙中,∵、都是所对的圆周角
∴
推论2:半圆或直径所对的圆周角是直角;圆周角是直角所对的弧是半圆,所对的弦是直径。
即:在⊙中,∵是直径 或∵
∴ ∴是直径
推论3:若三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
即:在△中,∵
∴△是直角三角形或
注:此推论实是初二年级几何中矩形的推论:在直角三角形中斜边上的中线等于斜边的一半的逆定理。
八、圆内接四边形
圆的内接四边形定理:圆的内接四边形的对角互补,外角等于它的内对角。
即:在⊙中,
∵四边形是内接四边形
∴
九、切线的性质与判定定理
(1)切线的判定定理:过半径外端且垂直于半径的直线是切线;
两个条件:过半径外端且垂直半径,二者缺一不可
即:∵且过半径外端
∴是⊙的切线
(2)性质定理:切线垂直于过切点的半径(如上图)
推论1:过圆心垂直于切线的直线必过切点。
推论2:过切点垂直于切线的直线必过圆心。
以上三个定理及推论也称二推一定理:
即:①过圆心;②过切点;③垂直切线,三个条件中知道其中两个条件就能推出最后一个。
十、切线长定理
切线长定理:
从圆外一点引圆的两条切线,它们的切线长相等,这点和圆心的连线平分两条切线的夹角。
即:∵、是的两条切线
∴
平分
十一、圆幂定理
(1)相交弦定理:圆内两弦相交,交点分得的两条线段的乘积相等。
即:在⊙中,∵弦、相交于点,
∴
(2)推论:如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项。
即:在⊙中,∵直径,
∴
(3)切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
即:在⊙中,∵是切线,是割线
∴
(4)割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等(如上图)。
即:在⊙中,∵、是割线
∴
十二、两圆公共弦定理
圆公共弦定理:两圆圆心的连线垂直并且平分这两个圆的的公共弦。
如图:垂直平分。
即:∵⊙、⊙相交于、两点
∴垂直平分
十三、圆的公切线
两圆公切线长的计算公式:
(1)公切线长:中,;
(2)外公切线长:是半径之差; 内公切线长:是半径之和 。
十四、圆内正多边形的计算
(1)正三角形
在⊙中△是正三角形,有关计算在中进行:;
(2)正四边形
同理,四边形的有关计算在中进行,:
(3)正六边形
同理,六边形的有关计算在中进行,.
十五、扇形、圆柱和圆锥的相关计算公式
1、扇形:(1)弧长公式:;
(2)扇形面积公式:
:圆心角 :扇形多对应的圆的半径 :扇形弧长 :扇形面积
2、圆柱:
(1)A圆柱侧面展开图
=
B圆柱的体积:
(2)A圆锥侧面展开图
=
B圆锥的体积:
第二十八章 样本与总体?
二.?重点、难点:
??1.?重点:
⑴了解普查与抽样调查的概念,并能根据实际情况确定收集数据的方式;
⑵了解总体、个体、样本等概念,能够指出研究对象的总体、个体与样本;
⑶学会用科学的随机抽样的方法,选取合适的样本进行抽样调查,用样本估计总体;
⑷通过整理和分析数据,准确地作出决策。
??2.?难点:
⑴正确识别问题中的总体、个体、样本、样本容量等,并能选择合适的样本看总体;
⑵能够对数据的来源,处理数据的方法,以及由此得到的结果进行合理的分析。
?
三.?知识梳理:
知识点 内容关注 注意事项
总体、个体、样本、样本容量 总体是考察对象的主体,个体是组成总体的每一个对象,样本是总体中的一部分个体,样本容量是样本包含的个体数量 样本容量是一个样本中个体的数量
普查与抽样调查 普查是对所有对象进行调查,抽样调查是对部分对象进行调查 普查与抽样调查的范围不同
简单的 随机抽样 使样本具有代表性,不偏向总体中的某些个体,对每个个体都公平的方法,就是用抽签的方法决定个体进入样本 简单的随机抽样对总体中每个个体来说,被抽到的机会是均等的
随机性 在抽样前,不能预测哪些个体会被抽中,这种不能事先预测结果的特性称为随机性 随机性是抽取样本具有代表性的重要保障
抽样调查 的可靠性 用随机抽样的方法获取样本,且样本容量合适时,由样本得出的特性会更接近总体的特性 ⑴样本在总体中需有代表性;
⑵样本容量应该足够大;
⑶样本要避免遗漏某一个群体
借助调查作决策 通过媒体收集信息,将信息进行全面、科学地分析 分析角度不同,得到的结论也会不同
容易误导决策 的统计图 媒体中数据很多,有许多有用的信息,但信息不一定可靠,要全面分析 考虑信息的时效性、可靠性和代表性
第二十六章 二次函数
一、二次函数概念:
1、二次函数的概念:一般地,形如(是常数,)的函数,叫做二次函数。
这里需要强调:和一元二次方程类似,二次项系数,而可以为零。二次函数的定义域是全体实数。
2、二次函数的结构特征:
⑴ 等号左边是函数,右边是关于自变量的二次式,的最高次数是2。
⑵ 是常数,是二次项系数,是一次项系数,是常数项。
二、二次函数的基本形式
1. 二次函数基本形式:的性质:a 的绝对值越大,抛物线的开口越小。
的符号 开口方向 顶点坐标 对称轴 性质
向上
轴 时,随的增大而增大;
时,随的增大而减小;
时,有最小值。
向下
轴 时,随的增大而减小;
时,随的增大而增大;
时,有最大值。
2. 的性质:
的符号 开口方向 顶点坐标 对称轴 性质
向上
轴 时,随的增大而增大;
时,随的增大而减小;
时,有最小值。
向下
轴 时,随的增大而减小;
时,随的增大而增大;
时,有最大值。
3. 的性质:
的符号 开口方向 顶点坐标 对称轴 性质
向上
X=h 时,随的增大而增大;
时,随的增大而减小;
时,有最小值。
向下
X=h 时,随的增大而减小;
时,随的增大而增大;
时,有最大值。
4. 的性质:
的符号 开口方向 顶点坐标 对称轴 性质
向上
X=h 时,随的增大而增大;时,随的增大而减小;时,有最小值。
向下
X=h 时,随的增大而减小;时,随的增大而增大;时,有最大值。
三、二次函数图象的平移
1. 平移步骤:
方法一:⑴ 将抛物线解析式转化成顶点式,确定其顶点坐标;
⑵ 保持抛物线的形状不变,将其顶点平移到处,具体平移方法如下:
2. 平移规律
在原有函数的基础上“值正右移,负左移;值正上移,负下移”。
概括成八个字“左加右减,上加下减”。
方法二:
⑴沿轴平移:向上(下)平移个单位,
变成(或)
⑵沿轴平移:向左(右)平移个单位,
变成(或)
四、二次函数与的比较
从解析式上看,与是两种不同的表达形式,后者通过配方可以得到前者,即,其中。
五、二次函数图象的画法
五点绘图法:利用配方法将二次函数化为顶点式,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:顶点、与轴的交点、以及关于对称轴对称的点、与轴的交点,(若与轴没有交点,则取两组关于对称轴对称的点).
画草图时应抓住以下几点:开口方向,对称轴,顶点,与轴的交点,与轴的交点.
六、二次函数的性质
1. 当时,抛物线开口向上,对称轴为,顶点坐标为。
当时,随的增大而减小;当时,随的增大而增大;当时,有最小值。
2. 当时,抛物线开口向下,对称轴为,顶点坐标为。当时,随的增大而增大;当时,随的增大而减小;当时,有最大值。
七、二次函数解析式的表示方法
1. 一般式:(,,为常数,);
2. 顶点式:(,,为常数,);
3. 两根式:(,,是抛物线与轴两交点的横坐标).
注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线与轴有交点,即时,抛物线的解析式才可以用交点式表示。二次函数解析式的这三种形式可以互化.
八、二次函数的图象与各项系数之间的关系
1. 二次项系数
二次函数中,作为二次项系数,显然。
⑴ 当时,抛物线开口向上,的值越大,开口越小,反之的值越小,开口越大;
⑵ 当时,抛物线开口向下,的值越小,开口越小,反之的值越大,开口越大。
总结起来,决定了抛物线开口的大小和方向,的正负决定开口方向,的大小决定开口的大小。
2. 一次项系数
在二次项系数确定的前提下,决定了抛物线的对称轴。
⑴ 在的前提下,
当时,,即抛物线的对称轴在轴左侧;
当时,,即抛物线的对称轴就是轴;
当时,,即抛物线对称轴在轴的右侧。
⑵ 在的前提下,结论刚好与上述相反,即
当时,,即抛物线的对称轴在轴右侧;
当时,,即抛物线的对称轴就是轴;
当时,,即抛物线对称轴在轴的左侧。
总结起来,在确定的前提下,决定了抛物线对称轴的位置。
的符号的判定:对称轴在轴左边则,在轴的右侧则,概括的说就是“左同右异”
总结:
3. 常数项
⑴ 当时,抛物线与轴的交点在轴上方,即抛物线与轴交点的纵坐标为正;
⑵ 当时,抛物线与轴的交点为坐标原点,即抛物线与轴交点的纵坐标为;
⑶ 当时,抛物线与轴的交点在轴下方,即抛物线与轴交点的纵坐标为负。
总结起来,决定了抛物线与轴交点的位置。
总之,只要都确定,那么这条抛物线就是唯一确定的。
二次函数解析式的确定:
根据已知条件确定二次函数解析式,通常利用待定系数法。用待定系数法求二次函数的解析式必须根据题目的特点,选择适当的形式,才能使解题简便。一般来说,有如下几种情况:
1. 已知抛物线上三点的坐标,一般选用一般式;
2. 已知抛物线顶点或对称轴或最大(小)值,一般选用顶点式;
3. 已知抛物线与轴的两个交点的横坐标,一般选用两根式;
4. 已知抛物线上纵坐标相同的两点,常选用顶点式。
九、二次函数图象的对称
二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达
1. 关于轴对称
关于轴对称后,得到的解析式是;
关于轴对称后,得到的解析式是;
2. 关于轴对称
关于轴对称后,得到的解析式是;
关于轴对称后,得到的解析式是;
3. 关于原点对称
关于原点对称后,得到的解析式是;
关于原点对称后,得到的解析式是;
4. 关于顶点对称(即:抛物线绕顶点旋转180°)
关于顶点对称后,得到的解析式是;
关于顶点对称后,得到的解析式是。
5. 关于点对称
关于点对称后,得到的解析式是
根据对称的性质,显然无论作何种对称变换,抛物线的形状一定不会发生变化,因此永远不变。求抛物线的对称抛物线的表达式时,可以依据题意或方便运算的原则,选择合适的形式,习惯上是先确定原抛物线(或表达式已知的抛物线)的顶点坐标及开口方向,再确定其对称抛物线的顶点坐标及开口方向,然后再写出其对称抛物线的表达式。
十、二次函数与一元二次方程:
1. 二次函数与一元二次方程的关系(二次函数与轴交点情况):
一元二次方程是二次函数当函数值时的特殊情况.
图象与轴的交点个数:
① 当时,图象与轴交于两点,其中的是一元二次方程的两根。这两点间的距离.
② 当时,图象与轴只有一个交点;
③ 当时,图象与轴没有交点.
当时,图象落在轴的上方,无论为任何实数,都有;
当时,图象落在轴的下方,无论为任何实数,都有。
2. 抛物线的图象与轴一定相交,交点坐标为,;
3. 二次函数常用解题方法总结:
⑴ 求二次函数的图象与轴的交点坐标,需转化为一元二次方程;
⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式;
⑶ 根据图象的位置判断二次函数中,,的符号,或由二次函数中,,的符号判断图象的位置,要数形结合;
⑷ 二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与轴的一个交点坐标,可由对称性求出另一个交点坐标.
⑸ 与二次函数有关的还有二次三项式,二次三项式本身就是所含字母的二次函数;下面以时为例,揭示二次函数、二次三项式和一元二次方程之间的内在联系:
抛物线与轴有两个交点 二次三项式的值可正、可零、可负 一元二次方程有两个不相等实根
抛物线与轴只有一个交点 二次三项式的值为非负 一元二次方程有两个相等的实数根
抛物线与轴无交点 二次三项式的值恒为正 一元二次方程无实数根.
二次函数图像参考:
十一、函数的应用
二次函数应用
第二十七章:《圆》
一、知识回顾
圆的周长: C=2πr或C=πd、圆的面积:S=πr?
圆环面积计算方法:S=πR?-πr?或S=π(R?-r?)(R是大圆半径,r是小圆半径)
二、知识要点
一、圆的概念
集合形式的概念: 1、 圆可以看作是到定点的距离等于定长的点的集合;
2、圆的外部:可以看作是到定点的距离大于定长的点的集合;
3、圆的内部:可以看作是到定点的距离小于定长的点的集合
轨迹形式的概念:
1、圆:到定点的距离等于定长的点的轨迹就是以定点为圆心,定长为半径的圆;
固定的端点O为圆心。连接圆上任意两点的线段叫做弦,经过圆心的弦叫直径。圆上任意两点之间的部分叫做圆弧,简称弧。
2、垂直平分线:到线段两端距离相等的点的轨迹是这条线段的垂直平分线;
3、角的平分线:到角两边距离相等的点的轨迹是这个角的平分线;
4、到直线的距离相等的点的轨迹是:平行于这条直线且到这条直线的距离等于定长的两条直线;
5、到两条平行线距离相等的点的轨迹是:平行于这两条平行线且到两条直线距离都相等的一条直线。
二、点与圆的位置关系
1、点在圆内 点在圆内;
2、点在圆上 点在圆上;
3、点在圆外 点在圆外;
三、直线与圆的位置关系
1、直线与圆相离 无交点;
2、直线与圆相切 有一个交点;
3、直线与圆相交 有两个交点;
四、圆与圆的位置关系
外离(图1) 无交点 ;
外切(图2) 有一个交点 ;
相交(图3) 有两个交点 ;
内切(图4) 有一个交点 ;
内含(图5) 无交点 ;
五、垂径定理
垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。
推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;
(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧
以上共4个定理,简称2推3定理:此定理中共5个结论中,只要知道其中2个即可推出其它3个结论,即:
①是直径 ② ③ ④ 弧弧 ⑤ 弧弧
中任意2个条件推出其他3个结论。
推论2:圆的两条平行弦所夹的弧相等。
即:在⊙中,∵∥
∴弧弧
六、圆心角定理
顶点到圆心的角,叫圆心角。
圆心角定理:同圆或等圆中,相等的圆心角所对的弦相等,所对的弧相等,弦心距相等。 此定理也称1推3定理,即上述四个结论中,
只要知道其中的1个相等,则可以推出其它的3个结论,
即:①;②;
③;④ 弧弧
七、圆周角定理
顶点在圆上,并且两边都与圆相交的角,叫圆周角。
1、圆周角定理:同弧所对的圆周角等于它所对的圆心的角的一半。
即:∵和是弧所对的圆心角和圆周角
∴
2、圆周角定理的推论:
推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧是等弧;
即:在⊙中,∵、都是所对的圆周角
∴
推论2:半圆或直径所对的圆周角是直角;圆周角是直角所对的弧是半圆,所对的弦是直径。
即:在⊙中,∵是直径 或∵
∴ ∴是直径
推论3:若三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
即:在△中,∵
∴△是直角三角形或
注:此推论实是初二年级几何中矩形的推论:在直角三角形中斜边上的中线等于斜边的一半的逆定理。
八、圆内接四边形
圆的内接四边形定理:圆的内接四边形的对角互补,外角等于它的内对角。
即:在⊙中,
∵四边形是内接四边形
∴
九、切线的性质与判定定理
(1)切线的判定定理:过半径外端且垂直于半径的直线是切线;
两个条件:过半径外端且垂直半径,二者缺一不可
即:∵且过半径外端
∴是⊙的切线
(2)性质定理:切线垂直于过切点的半径(如上图)
推论1:过圆心垂直于切线的直线必过切点。
推论2:过切点垂直于切线的直线必过圆心。
以上三个定理及推论也称二推一定理:
即:①过圆心;②过切点;③垂直切线,三个条件中知道其中两个条件就能推出最后一个。
十、切线长定理
切线长定理:
从圆外一点引圆的两条切线,它们的切线长相等,这点和圆心的连线平分两条切线的夹角。
即:∵、是的两条切线
∴
平分
十一、圆幂定理
(1)相交弦定理:圆内两弦相交,交点分得的两条线段的乘积相等。
即:在⊙中,∵弦、相交于点,
∴
(2)推论:如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项。
即:在⊙中,∵直径,
∴
(3)切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
即:在⊙中,∵是切线,是割线
∴
(4)割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等(如上图)。
即:在⊙中,∵、是割线
∴
十二、两圆公共弦定理
圆公共弦定理:两圆圆心的连线垂直并且平分这两个圆的的公共弦。
如图:垂直平分。
即:∵⊙、⊙相交于、两点
∴垂直平分
十三、圆的公切线
两圆公切线长的计算公式:
(1)公切线长:中,;
(2)外公切线长:是半径之差; 内公切线长:是半径之和 。
十四、圆内正多边形的计算
(1)正三角形
在⊙中△是正三角形,有关计算在中进行:;
(2)正四边形
同理,四边形的有关计算在中进行,:
(3)正六边形
同理,六边形的有关计算在中进行,.
十五、扇形、圆柱和圆锥的相关计算公式
1、扇形:(1)弧长公式:;
(2)扇形面积公式:
:圆心角 :扇形多对应的圆的半径 :扇形弧长 :扇形面积
2、圆柱:
(1)A圆柱侧面展开图
=
B圆柱的体积:
(2)A圆锥侧面展开图
=
B圆锥的体积:
第二十八章 样本与总体?
二.?重点、难点:
??1.?重点:
⑴了解普查与抽样调查的概念,并能根据实际情况确定收集数据的方式;
⑵了解总体、个体、样本等概念,能够指出研究对象的总体、个体与样本;
⑶学会用科学的随机抽样的方法,选取合适的样本进行抽样调查,用样本估计总体;
⑷通过整理和分析数据,准确地作出决策。
??2.?难点:
⑴正确识别问题中的总体、个体、样本、样本容量等,并能选择合适的样本看总体;
⑵能够对数据的来源,处理数据的方法,以及由此得到的结果进行合理的分析。
?
三.?知识梳理:
知识点 内容关注 注意事项
总体、个体、样本、样本容量 总体是考察对象的主体,个体是组成总体的每一个对象,样本是总体中的一部分个体,样本容量是样本包含的个体数量 样本容量是一个样本中个体的数量
普查与抽样调查 普查是对所有对象进行调查,抽样调查是对部分对象进行调查 普查与抽样调查的范围不同
简单的 随机抽样 使样本具有代表性,不偏向总体中的某些个体,对每个个体都公平的方法,就是用抽签的方法决定个体进入样本 简单的随机抽样对总体中每个个体来说,被抽到的机会是均等的
随机性 在抽样前,不能预测哪些个体会被抽中,这种不能事先预测结果的特性称为随机性 随机性是抽取样本具有代表性的重要保障
抽样调查 的可靠性 用随机抽样的方法获取样本,且样本容量合适时,由样本得出的特性会更接近总体的特性 ⑴样本在总体中需有代表性;
⑵样本容量应该足够大;
⑶样本要避免遗漏某一个群体
借助调查作决策 通过媒体收集信息,将信息进行全面、科学地分析 分析角度不同,得到的结论也会不同
容易误导决策 的统计图 媒体中数据很多,有许多有用的信息,但信息不一定可靠,要全面分析 考虑信息的时效性、可靠性和代表性
