人教版数学七年级下册5.1.1相交线 课件(37张)
文档属性
| 名称 | 人教版数学七年级下册5.1.1相交线 课件(37张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 814.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 00:00:00 | ||
图片预览








文档简介
人教版 · 数学· 七年级(下)
第5章 相交线与平行线
5.1.1 相交线
1.理解邻补角与对顶角的概念。
2.掌握邻补角与对顶角的性质,并能运用它们的性质进行角的计算及解决简单实际问题。
学习目标
握紧剪刀把手时,随着两个把手之间的角逐渐变小,剪刀刃之间的角也相应变小,直到剪开布片.如果把剪刀的构造看作两条相交的直线,这就关系到两条相交直线所成的角的问题.
导入新知
A
O
C
B
D
∠AOC 和∠AOD有一条公共边AO,且∠AOC 的另一边是∠AOD 另一边的反向延长线.
新知一 邻补角与对顶角的概念
剪刀剪东西的过程中,你能说说∠AOC 与∠AOD
的位置保持怎样的关系吗?
合作探究
1
2
3
A
B
C
D
O
如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角.
如图中∠1 和∠2,∠1 和∠3 都互为邻补角.
互为邻补角是互为补角的特殊情况. ∠1 +∠2=180°, ∠1 +∠3 =180°.
(1)互为邻补角的两个角必须满足以下条件:①有一条公共边;②另一条边互为反向延长线. 二者缺一不可.
(2)邻补角不一定是两条直线相交形成的,如果一条直线与射线(端点在直线上)相交,也可以得到一对邻补角.
(3)互为邻补角的两个角一定互补,但互补的两个角不一定是邻补角.
∠AOC 和∠BOD 有公共顶点,且∠AOC 的两边分别是∠BOD 两边的反向延长线.
剪刀剪东西的过程中,你能说说∠AOC 与∠BOD
的位置保持怎样的关系吗?
A
O
C
B
D
1
2
A
B
C
D
O
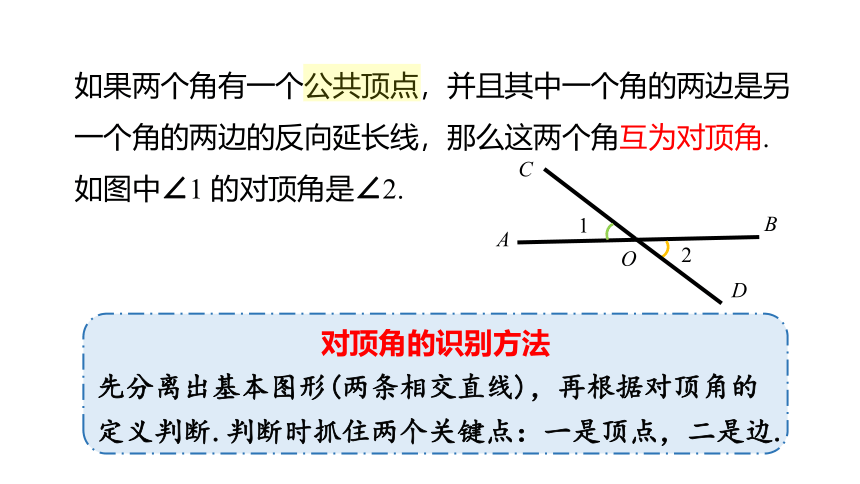
如果两个角有一个公共顶点,并且其中一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角.如图中∠1 的对顶角是∠2.
对顶角的识别方法
先分离出基本图形(两条相交直线),再根据对顶角的定义判断.判断时抓住两个关键点:一是顶点,二是边.
(1)两个角互为对顶角必须满足两个条件:①两个角有一个公共顶点;②一个角的两边分别是另一个角的两边的反向延长线.二者缺一不可.
(2)对顶角是成对出现的,指两个角之间的关系,一个角的对顶角只有一个.
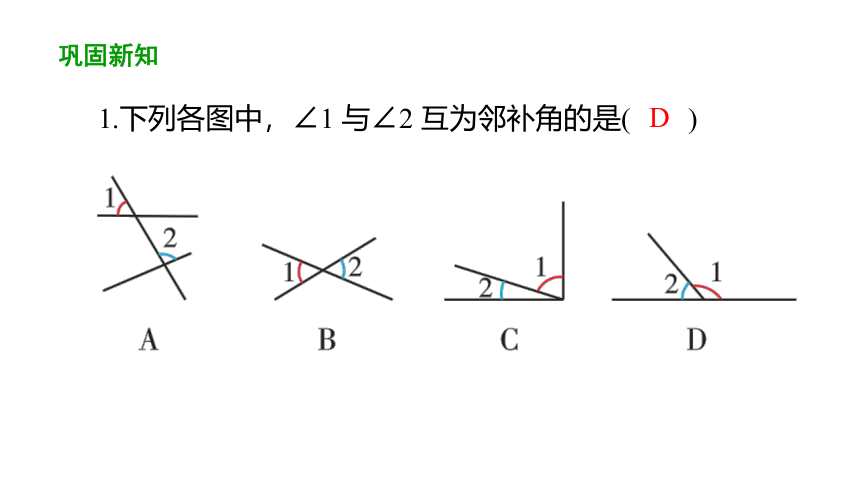
1.下列各图中,∠1 与∠2 互为邻补角的是( )
D
巩固新知
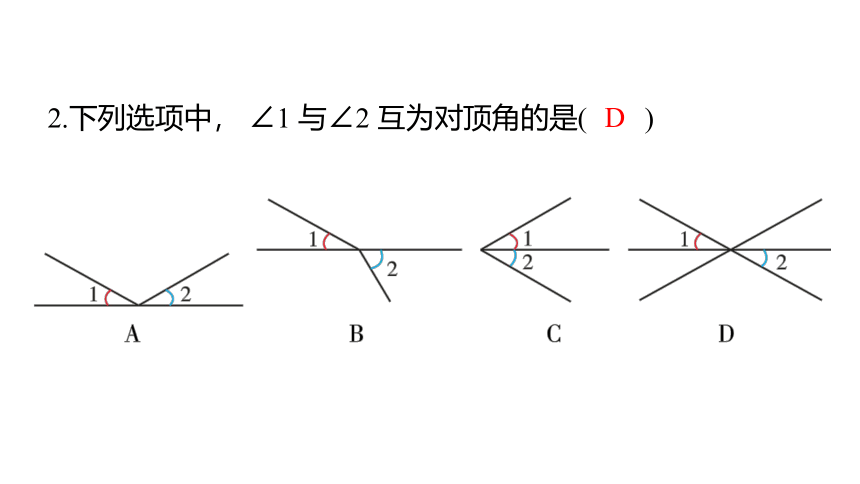
2.下列选项中, ∠1 与∠2 互为对顶角的是( )
D
新知二 对顶角的性质
C
O
A
B
D
4
3
2
1
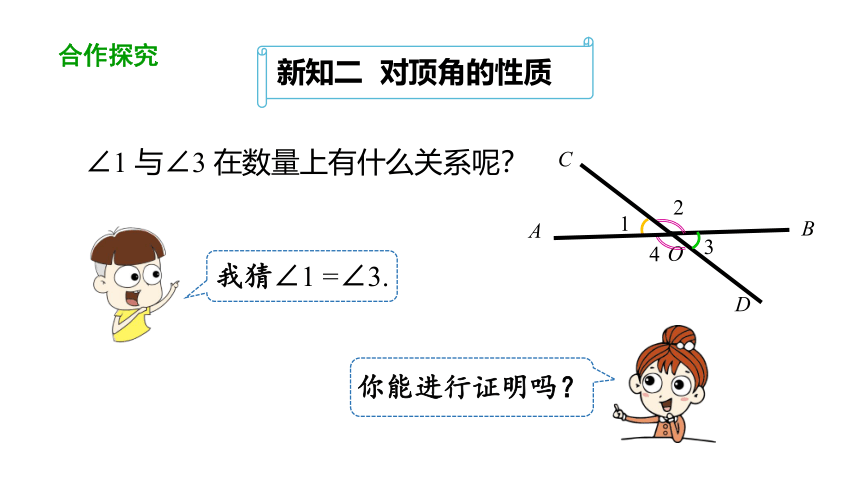
∠1 与∠3 在数量上有什么关系呢?
我猜∠1 =∠3.
你能进行证明吗?
合作探究
已知:直线 AB 与 CD 相交于 O 点.
证明:∠1=∠3.
解:因为直线 AB 与 CD 相交于 O 点,
所以∠1+∠2=180°,
∠2+∠3=180°,
所以∠1=∠3.
同理可得∠2=∠4.
C
O
A
B
D
4
3
2
1
应用格式:因为直线 AB 与 CD 相交于 O 点,
所以∠1=∠3,∠2=∠4.
对顶角相等.
C
O
A
B
D
4
3
2
1
两个角互为对顶角,它们一定相等,但相等的两个角不一定互为对顶角.
图中是对顶角量角器,你能说出用它测量角的
度数的原理吗?
对顶角相等.
例 如图,直线 a,b 相交,∠1=40°,求 ∠2,∠3,∠4 的度数.
解:由邻补角的定义,得
∠2= 180°-∠1=140°;
由对顶角相等,得∠3=∠1,∠1=40°,
所以∠3=40°,
∠4=∠2=140°.
1
2
3
4
a
b
1.如图,直线 AB,CD 相交于点 O,∠COE=145°,OD平分 ∠BOE,求 ∠AOC 的度数.
解:因为 ∠COE = 145°,
所以 ∠DOE = 180°-∠COE = 180°- 145° =35°.
因为 OD 平分 ∠BOE,
所以 ∠BOD=∠DOE =35°,
所以 ∠AOC=∠BOD =35°.
巩固新知
2.如图,直线 AB,CD,EF 相交于点 O,∠AOE = 40°,∠BOC = 2∠AOC,求∠DOF 的度数.
解:设∠AOC = x,则∠BOC = 2x.
由邻补角的性质可得 x+2x = 180°,
解得 x = 60°,即∠AOC= 60°,
所以 ∠EOC=∠AOC- ∠AOE = 60°-40°= 20°,
由对顶角相等得 ∠DOF =∠EOC = 20°.
运用方程计算角
当题目中出现比值或倍数关系时,可以用一个量表示另一个量,推导求解;也可以考虑先设未知数,然后通过等量关系列出关于未知数的方程,从而解决问题.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
对顶角
邻补角
特 征
①两条直线相交形成的角
②有公共顶点
③没有公共边
①两条直线相交而成的角
②有公共顶点
③有一条公共边
性 质
对顶角相等
邻补角互补
相同点
①都是两条直线相交而成的角
②都有一个公共顶点
③都是成对出现的
不同点
①有无公共边
②两直线相交时,对顶角只有两对,邻补角有四对
归纳新知
1.下列选项中,∠1与∠2互为对顶角的是( )
D
课堂练习
2.(2017·贺州)下列各图中,∠1与∠2互为邻补角的是( )
D
3.如图,直线AB,CD,EF相交于点O,则∠COF的一个邻补角是( )
A.∠BOF
B.∠DOF
C.∠AOE
D.∠DOE
B
4.邻补角是( )
A.和为180°的两个角
B.有公共顶点且互补的两个角
C.有一条公共边且互补的两个角
D.有公共顶点且有一条公共边,另一边互为反向延长线的两个角
D
5.下列说法正确的是( )
A.大小相等的两个角互为对顶角
B.有公共顶点且相等的两个角是对顶角
C.两直线相交所成的角互为对顶角
D.两边互为反向延长线且有公共顶点的两个角互为对顶角
D
6.(2017·河池)如图,点O在直线AB上,若∠BOC=60°,则∠AOC的大小是( )
A.60° B.90° C.120° D.150°
C
7.如图,直线l1与l2相交于点O,若∠1和∠2的和为130°,则∠3为( )
A.50°
B.130°
C.125°
D.115°
D
8.如图,直线AB,CD相交于点O.射线OM平分∠AOC,若∠BOD=76°,则∠BOM等于( )
A.38°
B.104°
C.142°
D.144°
C
9.如图,点O是直线AB上一点,OE,OF分别平分∠AOC和∠BOC,当OC的位置发生变化时(不与直线AB重合),那么∠EOF的度数( )
A.不变,都等于90°
B.逐渐变大
C.逐渐变小
D.无法确定
A
10.如图,直线AB,CD相交于点O,OE⊥CD,OF⊥AB,∠DOF=65°,则∠BOE=___________,∠AOC=___________.
65°
25°
11.如图,已知直线EF交直线AB,CD于点G,H,∠1=∠2,∠3=120°,求∠4的度数.
解:因为∠3=120°,∠2+∠3=180°,所以∠2=60°.
因为∠1=∠2=60°,所以∠4=∠1=60°.
12.如图,已知直线AB与直线CD相交,∠1-∠2=50°,求∠1,∠2,∠3,∠4的度数.
解:设∠2=x°,则∠1=(180-x)°,
由∠1-∠2=50°得x=65,
∴∠1=∠3=115°,∠2=∠4=65°.
13.如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COE,且∠1∶∠2=1∶4,求∠AOC和∠AOF的度数.
解:因为OE平分∠BOD,
所以∠1=∠BOE.
因为∠1∶∠2=1∶4,所以设∠1=x°,则∠EOB=x°,∠2=4x°,
所以x+x+4x=180°,解得x=30.
所以∠1=30°,∠DOB=60°.
所以∠COE=150°,∠AOC=∠DOB=60°.
又因为OF平分∠COE,
所以∠COF=75°.
所以∠AOF=∠AOC+∠COF=60°+75°=135°.
再见
第5章 相交线与平行线
5.1.1 相交线
1.理解邻补角与对顶角的概念。
2.掌握邻补角与对顶角的性质,并能运用它们的性质进行角的计算及解决简单实际问题。
学习目标
握紧剪刀把手时,随着两个把手之间的角逐渐变小,剪刀刃之间的角也相应变小,直到剪开布片.如果把剪刀的构造看作两条相交的直线,这就关系到两条相交直线所成的角的问题.
导入新知
A
O
C
B
D
∠AOC 和∠AOD有一条公共边AO,且∠AOC 的另一边是∠AOD 另一边的反向延长线.
新知一 邻补角与对顶角的概念
剪刀剪东西的过程中,你能说说∠AOC 与∠AOD
的位置保持怎样的关系吗?
合作探究
1
2
3
A
B
C
D
O
如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角.
如图中∠1 和∠2,∠1 和∠3 都互为邻补角.
互为邻补角是互为补角的特殊情况. ∠1 +∠2=180°, ∠1 +∠3 =180°.
(1)互为邻补角的两个角必须满足以下条件:①有一条公共边;②另一条边互为反向延长线. 二者缺一不可.
(2)邻补角不一定是两条直线相交形成的,如果一条直线与射线(端点在直线上)相交,也可以得到一对邻补角.
(3)互为邻补角的两个角一定互补,但互补的两个角不一定是邻补角.
∠AOC 和∠BOD 有公共顶点,且∠AOC 的两边分别是∠BOD 两边的反向延长线.
剪刀剪东西的过程中,你能说说∠AOC 与∠BOD
的位置保持怎样的关系吗?
A
O
C
B
D
1
2
A
B
C
D
O
如果两个角有一个公共顶点,并且其中一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角.如图中∠1 的对顶角是∠2.
对顶角的识别方法
先分离出基本图形(两条相交直线),再根据对顶角的定义判断.判断时抓住两个关键点:一是顶点,二是边.
(1)两个角互为对顶角必须满足两个条件:①两个角有一个公共顶点;②一个角的两边分别是另一个角的两边的反向延长线.二者缺一不可.
(2)对顶角是成对出现的,指两个角之间的关系,一个角的对顶角只有一个.
1.下列各图中,∠1 与∠2 互为邻补角的是( )
D
巩固新知
2.下列选项中, ∠1 与∠2 互为对顶角的是( )
D
新知二 对顶角的性质
C
O
A
B
D
4
3
2
1
∠1 与∠3 在数量上有什么关系呢?
我猜∠1 =∠3.
你能进行证明吗?
合作探究
已知:直线 AB 与 CD 相交于 O 点.
证明:∠1=∠3.
解:因为直线 AB 与 CD 相交于 O 点,
所以∠1+∠2=180°,
∠2+∠3=180°,
所以∠1=∠3.
同理可得∠2=∠4.
C
O
A
B
D
4
3
2
1
应用格式:因为直线 AB 与 CD 相交于 O 点,
所以∠1=∠3,∠2=∠4.
对顶角相等.
C
O
A
B
D
4
3
2
1
两个角互为对顶角,它们一定相等,但相等的两个角不一定互为对顶角.
图中是对顶角量角器,你能说出用它测量角的
度数的原理吗?
对顶角相等.
例 如图,直线 a,b 相交,∠1=40°,求 ∠2,∠3,∠4 的度数.
解:由邻补角的定义,得
∠2= 180°-∠1=140°;
由对顶角相等,得∠3=∠1,∠1=40°,
所以∠3=40°,
∠4=∠2=140°.
1
2
3
4
a
b
1.如图,直线 AB,CD 相交于点 O,∠COE=145°,OD平分 ∠BOE,求 ∠AOC 的度数.
解:因为 ∠COE = 145°,
所以 ∠DOE = 180°-∠COE = 180°- 145° =35°.
因为 OD 平分 ∠BOE,
所以 ∠BOD=∠DOE =35°,
所以 ∠AOC=∠BOD =35°.
巩固新知
2.如图,直线 AB,CD,EF 相交于点 O,∠AOE = 40°,∠BOC = 2∠AOC,求∠DOF 的度数.
解:设∠AOC = x,则∠BOC = 2x.
由邻补角的性质可得 x+2x = 180°,
解得 x = 60°,即∠AOC= 60°,
所以 ∠EOC=∠AOC- ∠AOE = 60°-40°= 20°,
由对顶角相等得 ∠DOF =∠EOC = 20°.
运用方程计算角
当题目中出现比值或倍数关系时,可以用一个量表示另一个量,推导求解;也可以考虑先设未知数,然后通过等量关系列出关于未知数的方程,从而解决问题.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
对顶角
邻补角
特 征
①两条直线相交形成的角
②有公共顶点
③没有公共边
①两条直线相交而成的角
②有公共顶点
③有一条公共边
性 质
对顶角相等
邻补角互补
相同点
①都是两条直线相交而成的角
②都有一个公共顶点
③都是成对出现的
不同点
①有无公共边
②两直线相交时,对顶角只有两对,邻补角有四对
归纳新知
1.下列选项中,∠1与∠2互为对顶角的是( )
D
课堂练习
2.(2017·贺州)下列各图中,∠1与∠2互为邻补角的是( )
D
3.如图,直线AB,CD,EF相交于点O,则∠COF的一个邻补角是( )
A.∠BOF
B.∠DOF
C.∠AOE
D.∠DOE
B
4.邻补角是( )
A.和为180°的两个角
B.有公共顶点且互补的两个角
C.有一条公共边且互补的两个角
D.有公共顶点且有一条公共边,另一边互为反向延长线的两个角
D
5.下列说法正确的是( )
A.大小相等的两个角互为对顶角
B.有公共顶点且相等的两个角是对顶角
C.两直线相交所成的角互为对顶角
D.两边互为反向延长线且有公共顶点的两个角互为对顶角
D
6.(2017·河池)如图,点O在直线AB上,若∠BOC=60°,则∠AOC的大小是( )
A.60° B.90° C.120° D.150°
C
7.如图,直线l1与l2相交于点O,若∠1和∠2的和为130°,则∠3为( )
A.50°
B.130°
C.125°
D.115°
D
8.如图,直线AB,CD相交于点O.射线OM平分∠AOC,若∠BOD=76°,则∠BOM等于( )
A.38°
B.104°
C.142°
D.144°
C
9.如图,点O是直线AB上一点,OE,OF分别平分∠AOC和∠BOC,当OC的位置发生变化时(不与直线AB重合),那么∠EOF的度数( )
A.不变,都等于90°
B.逐渐变大
C.逐渐变小
D.无法确定
A
10.如图,直线AB,CD相交于点O,OE⊥CD,OF⊥AB,∠DOF=65°,则∠BOE=___________,∠AOC=___________.
65°
25°
11.如图,已知直线EF交直线AB,CD于点G,H,∠1=∠2,∠3=120°,求∠4的度数.
解:因为∠3=120°,∠2+∠3=180°,所以∠2=60°.
因为∠1=∠2=60°,所以∠4=∠1=60°.
12.如图,已知直线AB与直线CD相交,∠1-∠2=50°,求∠1,∠2,∠3,∠4的度数.
解:设∠2=x°,则∠1=(180-x)°,
由∠1-∠2=50°得x=65,
∴∠1=∠3=115°,∠2=∠4=65°.
13.如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COE,且∠1∶∠2=1∶4,求∠AOC和∠AOF的度数.
解:因为OE平分∠BOD,
所以∠1=∠BOE.
因为∠1∶∠2=1∶4,所以设∠1=x°,则∠EOB=x°,∠2=4x°,
所以x+x+4x=180°,解得x=30.
所以∠1=30°,∠DOB=60°.
所以∠COE=150°,∠AOC=∠DOB=60°.
又因为OF平分∠COE,
所以∠COF=75°.
所以∠AOF=∠AOC+∠COF=60°+75°=135°.
再见
