人教版数学七年级下册5.1.2垂线 课件(45张)
文档属性
| 名称 | 人教版数学七年级下册5.1.2垂线 课件(45张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 00:00:00 | ||
图片预览









文档简介
人教版 · 数学· 七年级(下)
第5章 相交线与平行线
5.1.2 垂线
1.理解垂线的有关概念、性质及画法。
2.知道垂线段和点到直线的距离的概念,并会应用其解决问题。
学习目标
1
2
3
4
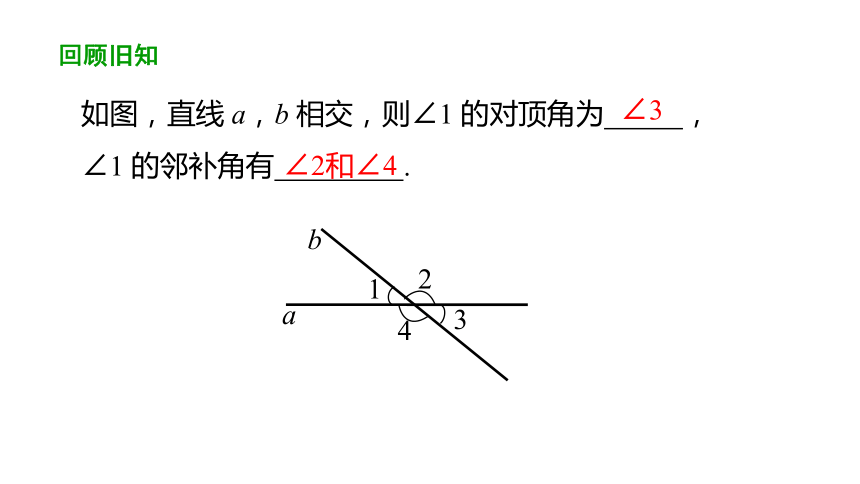
a
b
如图,直线 a,b 相交,则∠1 的对顶角为 ,
∠1 的邻补角有 .
∠3
∠2和∠4
回顾旧知
观察下面的图片,你能找出其中相交的直线吗?它们有什么特殊的位置关系?
导入新知
日常生活中,图中的两条直线的关系很常见,你能举出其他例子吗?
新知一 垂线的概念
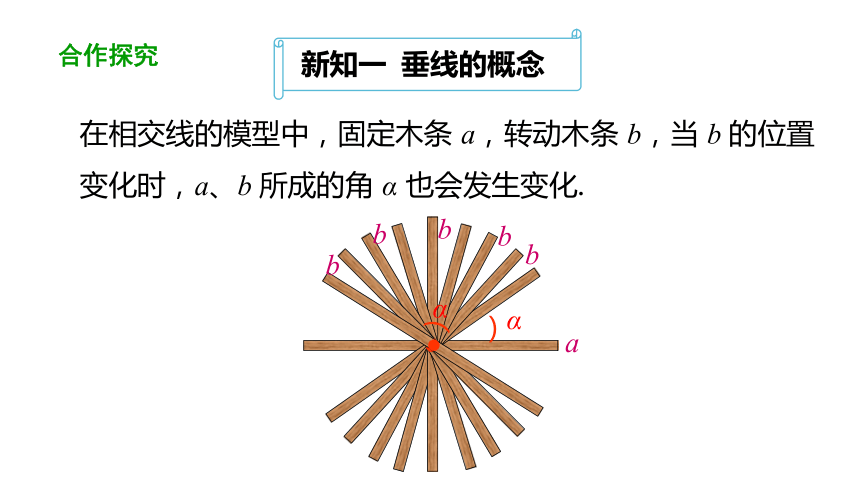
在相交线的模型中,固定木条 a,转动木条 b,当 b 的位置变化时,a、b 所成的角 α 也会发生变化.
)
α
a
b
b
b
b
b
)
α
合作探究
如图,当∠AOC=90° 时,∠BOD、∠AOD、∠BOC 的度数是多少?
A
B
C
D
O
由对顶角和邻补角的性质可知,当∠AOC=90°时,∠BOD=∠AOD=∠BOC=90°.
垂线:当两条直线相交所成的四个角中有一个角为90°时,这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
两条直线互相垂直是它们相交的一种特殊情况.
如图,直线 AB 与 CD 相交于点 O,若∠BOC = 90°,则AB,CD 互相垂直,记作“AB⊥CD”,读作“AB 垂直于 CD”,直线 AB 叫做直线 CD 的垂线(或直线 CD 叫做直线 AB 的垂线),交点 O 叫做垂足.
垂直的表示法:
如果用 l、m 表示这两条直线,那么直线 l 与直线 m 垂直,可记作:l⊥m (或 m⊥l ).
A
B
C
D
O
l
m
垂线的定义具有双重作用:
①知线垂直得直角;
②知直角得线垂直.
A
B
C
D
O
如图,①若 AB⊥CD,则∠BOC =∠AOC =∠AOD =
∠BOD =90°;
②若∠BOC =90°,则 AB⊥CD.
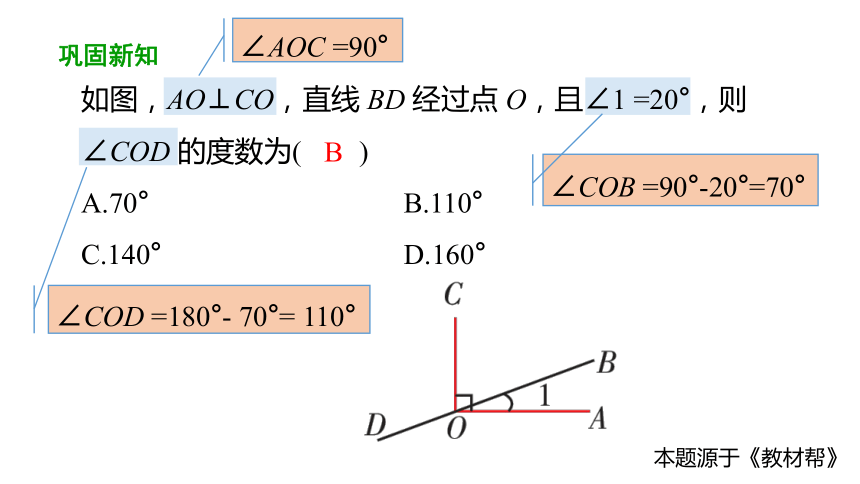
如图,AO⊥CO,直线 BD 经过点 O,且∠1 =20°,则∠COD 的度数为( )
A.70° B.110°
C.140° D.160°
∠AOC =90°
∠COB =90°-20°=70°
∠COD =180°- 70°= 110°
B
本题源于《教材帮》
巩固新知
新知二 垂线的画法及性质
A
.B
l
.
(1)画已知直线l的垂线能画几条?
(2)过直线 l 上的一点A画l的垂线,这样的垂线能画几条?
(3)过直线 l 外的一点B画l的垂线,这样的垂线能画几条?
合作探究
1.落.
2.画.
l
O
如图,已知直线 l,作 l 的垂线.
A
这样画直线 l 的垂线可以画几条?
无数条.
l
A
B
1.落.
2.移.
3.画.
如图,已知直线 l 和 l 上的一点 A,过点 A 作 l 的垂线.
一条.
这样画直线 l 的垂线可以画几条?
l
A
B
1.落.
2.移.
3.画.
如图,已知直线 l 和 l 外的一点 A ,过点 A 作 l 的垂线.
一条.
这样画直线 l 的垂线可以画几条?
经过一点画已知直线的垂线,通常有两种画法.
(1)用三角尺画:
落:让三角尺的一条直角边落在已知直线上,使其与 已知直线重合.
移:沿已知直线移动三角尺,使其另一条直角边经过已知点.
画:沿此直角边画直线,则这条直线就是已知直线的垂线.
1
2
3
点 A 在直线 l 上
点 A 在直线 l 外
(2)用量角器画:
l
A
l
A
垂线的性质:在同一平面内,过一点有且只有一条直线与已知直线垂直.
1.不能忽略“在同一平面内”这个条件,因为如果不在同一平面内,那么过一点有无数条直线与已知直线垂直;
2.“过一点”中的点,可以在已知直线上,也可以在已知直线外;
3.“有且只有”中,“有”指存在,“只有”指唯一性.
(1)在同一平面内,已知直线的垂线有无数条,但过一点画已知直线的垂线只能画出一条.
(2)画一条线段或射线的垂线,就是画它们所在直线的垂线,垂足可能在这条线段或射线上,也可能在线段的延长线上或射线的反向延长线上.
如图,分别过点 P 作线段 MN 的垂线.
M
N
P
M
N
P
Q
P
M
N
Q
P
M
N
Q
巩固新知
新知三 点到直线的距离
C
D
E
l
再从点 A 向已知直线 l 画几条不垂直的线段.
B
A
如图,点 A 为直线 l 外一点,AD⊥l,垂足为D,称 AD为点 A到直线 l 的垂线段.
线段 AB,AC,AD,AE 中谁最短?你能用一句话表示这个结论吗?
合作探究
垂线段的性质:连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短.
点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
如图,线段 AD 的长度是点 A 到直线 l 的距离.
C
D
E
l
B
A
(1)连接直线外一点与直线上各点有无数条线段,但垂线段只有一条.
(2)垂线是一条直线,长度不可以度量,而垂线段是一条线段,长度可以度量.
(3)垂线段是几何图形,而点到直线的距离是点到直线的垂线段的长度,是一个数量.
在灌溉时,要把河中的水引到农田 P 处,如何挖渠能使渠道最短?请在图中画出来,并说明理由.
m
垂线段最短.
如图所示,在直角三角形 ABC 中,AB⊥AC,过点 A 作 AD⊥BC,垂足为 D,已知 AB = 6 cm,AD = 5 cm.
(1)点 B 到 AC 的距离为_____,点 A 到 BC 的距离为 .
(2)CD AC(填“>”“<”或“=”),依据是 .
线段 AB 的长度
线段 AD 的长度
6 cm
5 cm
点 C 到直线 AD 的垂线段
<
垂线段最短
巩固新知
垂线
垂线和垂线段
定义
性质
垂线段
定义
性质
点到直线的距离
归纳新知
1.如图,OA⊥OB,∠1=35°,则∠2的度数是( )
A.35° B.45° C.55° D.70°
C
课堂练习
2.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠AOC=70°,则∠CON的度数为( )
A.65° B.55° C.45° D.35°
B
3.(1)如图①,O为直线AB上一点,且OC⊥OD,若∠1=25°,则∠2的度数为___________;
65°
(2)如图②,直线AB,CD相交于点O,OE为射线,若∠1=30°,∠2=120°,则OE与AB的位置关系是______________,可记作____________________.
垂直
OE⊥AB
4.过一条线段外一点,作这条线段的垂线,垂足在( )
A.这条线段上 B.这条线段的端点处
C.这条线段的延长线上 D.以上都可以
D
5.下列各图中,过直线l外一点P画l的垂线CD,三角板操作正确的是( )
D
6.(2017·柳州)如图,经过直线l外一点画l的垂线,能画出( )
A.1条 B.2条 C.3条 D.4条
A
7.如图,欲在AB上的某处D点修建一水泵站,将水引到村庄C处,可在图中画出D点,使C,D间铺设的管道最短,这种设计的依据是( )
A.两点之间,线段最短
B.两点确定一条直线
C.垂线段最短
D.过一点有且只有一条直线和已知直线垂直
C
8.如图所示,点P到直线l的距离是( )
A.线段PA的长度
B.线段PB的长度
C.线段PC的长度
D.线段PD的长度
B
9.如图所示,AB⊥AC,AD⊥BC,垂足分别为点A,D,AB=6 cm,AD=5 cm,则点B到直线AC的距离是________,点A到直线BC的距离是__________.
6 cm
5 cm
10.(1)在图①中,过AB外一点M作AB的垂线;
(2)在图②中,过点A,B分别作OB,OA的垂线.
解:(1)如图①所示.
(2)如图②所示.
11.如图,三条直线相交于点O,若CO⊥AB,∠1=56°,则∠2等于( )
A.30° B.34° C.45° D.56°
B
12.(2017·东明县期中)如图,直线a,b相交于点O,OE⊥a于点O,OF⊥b于点O,若∠1=40°,则下列结论正确的是( )
A.∠2=∠3=50°
B.∠2=∠3=40°
C.∠2=40°,∠3=50°
D.∠2=50°,∠3=40°
C
13.如图,AB⊥CD,垂足为点B,EF平分∠ABD,则∠CBF的度数为_________°.
45
14.如图,已知直线CD,EF相交于点O,OA⊥OB,且OE平分∠AOC,若∠EOC=60°,则∠BOF=______________.
30°
15.如图,在直线MN的异侧有A,B两点,按要求画图取点,并注明画图取点的依据.
(1)在直线MN上取一点C,使线段AC最短.依据是_____________________________;
(2)在直线MN上取一点D,使线段AD+BD最短.依据是____________________________.
垂线段最短
两点之间线段最短
解:(1)如图所示,点C即为所求点.
(2)如图所示,点D即为所求点.
16.如图,平原上有A,B,C,D四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池.
(1)不考虑其他因素,请你画图确定蓄水池H点的位置,使它到四个村庄的距离之和最小;
(2)计划把河水引入蓄水池H中,怎样开渠最短?并说明根据.
解:(1)因为两点之间线段最短,所以连接AD,BC交于点H,则H为蓄水池的位置,它到四个村庄的距离之和最小.
(2)过点H作HG⊥EF,垂足为点G.“过直线外一点与直线上各点的连线中,垂线段最短”是把河水引入蓄水池H中开渠最短的根据.
再见
第5章 相交线与平行线
5.1.2 垂线
1.理解垂线的有关概念、性质及画法。
2.知道垂线段和点到直线的距离的概念,并会应用其解决问题。
学习目标
1
2
3
4
a
b
如图,直线 a,b 相交,则∠1 的对顶角为 ,
∠1 的邻补角有 .
∠3
∠2和∠4
回顾旧知
观察下面的图片,你能找出其中相交的直线吗?它们有什么特殊的位置关系?
导入新知
日常生活中,图中的两条直线的关系很常见,你能举出其他例子吗?
新知一 垂线的概念
在相交线的模型中,固定木条 a,转动木条 b,当 b 的位置变化时,a、b 所成的角 α 也会发生变化.
)
α
a
b
b
b
b
b
)
α
合作探究
如图,当∠AOC=90° 时,∠BOD、∠AOD、∠BOC 的度数是多少?
A
B
C
D
O
由对顶角和邻补角的性质可知,当∠AOC=90°时,∠BOD=∠AOD=∠BOC=90°.
垂线:当两条直线相交所成的四个角中有一个角为90°时,这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
两条直线互相垂直是它们相交的一种特殊情况.
如图,直线 AB 与 CD 相交于点 O,若∠BOC = 90°,则AB,CD 互相垂直,记作“AB⊥CD”,读作“AB 垂直于 CD”,直线 AB 叫做直线 CD 的垂线(或直线 CD 叫做直线 AB 的垂线),交点 O 叫做垂足.
垂直的表示法:
如果用 l、m 表示这两条直线,那么直线 l 与直线 m 垂直,可记作:l⊥m (或 m⊥l ).
A
B
C
D
O
l
m
垂线的定义具有双重作用:
①知线垂直得直角;
②知直角得线垂直.
A
B
C
D
O
如图,①若 AB⊥CD,则∠BOC =∠AOC =∠AOD =
∠BOD =90°;
②若∠BOC =90°,则 AB⊥CD.
如图,AO⊥CO,直线 BD 经过点 O,且∠1 =20°,则∠COD 的度数为( )
A.70° B.110°
C.140° D.160°
∠AOC =90°
∠COB =90°-20°=70°
∠COD =180°- 70°= 110°
B
本题源于《教材帮》
巩固新知
新知二 垂线的画法及性质
A
.B
l
.
(1)画已知直线l的垂线能画几条?
(2)过直线 l 上的一点A画l的垂线,这样的垂线能画几条?
(3)过直线 l 外的一点B画l的垂线,这样的垂线能画几条?
合作探究
1.落.
2.画.
l
O
如图,已知直线 l,作 l 的垂线.
A
这样画直线 l 的垂线可以画几条?
无数条.
l
A
B
1.落.
2.移.
3.画.
如图,已知直线 l 和 l 上的一点 A,过点 A 作 l 的垂线.
一条.
这样画直线 l 的垂线可以画几条?
l
A
B
1.落.
2.移.
3.画.
如图,已知直线 l 和 l 外的一点 A ,过点 A 作 l 的垂线.
一条.
这样画直线 l 的垂线可以画几条?
经过一点画已知直线的垂线,通常有两种画法.
(1)用三角尺画:
落:让三角尺的一条直角边落在已知直线上,使其与 已知直线重合.
移:沿已知直线移动三角尺,使其另一条直角边经过已知点.
画:沿此直角边画直线,则这条直线就是已知直线的垂线.
1
2
3
点 A 在直线 l 上
点 A 在直线 l 外
(2)用量角器画:
l
A
l
A
垂线的性质:在同一平面内,过一点有且只有一条直线与已知直线垂直.
1.不能忽略“在同一平面内”这个条件,因为如果不在同一平面内,那么过一点有无数条直线与已知直线垂直;
2.“过一点”中的点,可以在已知直线上,也可以在已知直线外;
3.“有且只有”中,“有”指存在,“只有”指唯一性.
(1)在同一平面内,已知直线的垂线有无数条,但过一点画已知直线的垂线只能画出一条.
(2)画一条线段或射线的垂线,就是画它们所在直线的垂线,垂足可能在这条线段或射线上,也可能在线段的延长线上或射线的反向延长线上.
如图,分别过点 P 作线段 MN 的垂线.
M
N
P
M
N
P
Q
P
M
N
Q
P
M
N
Q
巩固新知
新知三 点到直线的距离
C
D
E
l
再从点 A 向已知直线 l 画几条不垂直的线段.
B
A
如图,点 A 为直线 l 外一点,AD⊥l,垂足为D,称 AD为点 A到直线 l 的垂线段.
线段 AB,AC,AD,AE 中谁最短?你能用一句话表示这个结论吗?
合作探究
垂线段的性质:连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短.
点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
如图,线段 AD 的长度是点 A 到直线 l 的距离.
C
D
E
l
B
A
(1)连接直线外一点与直线上各点有无数条线段,但垂线段只有一条.
(2)垂线是一条直线,长度不可以度量,而垂线段是一条线段,长度可以度量.
(3)垂线段是几何图形,而点到直线的距离是点到直线的垂线段的长度,是一个数量.
在灌溉时,要把河中的水引到农田 P 处,如何挖渠能使渠道最短?请在图中画出来,并说明理由.
m
垂线段最短.
如图所示,在直角三角形 ABC 中,AB⊥AC,过点 A 作 AD⊥BC,垂足为 D,已知 AB = 6 cm,AD = 5 cm.
(1)点 B 到 AC 的距离为_____,点 A 到 BC 的距离为 .
(2)CD AC(填“>”“<”或“=”),依据是 .
线段 AB 的长度
线段 AD 的长度
6 cm
5 cm
点 C 到直线 AD 的垂线段
<
垂线段最短
巩固新知
垂线
垂线和垂线段
定义
性质
垂线段
定义
性质
点到直线的距离
归纳新知
1.如图,OA⊥OB,∠1=35°,则∠2的度数是( )
A.35° B.45° C.55° D.70°
C
课堂练习
2.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠AOC=70°,则∠CON的度数为( )
A.65° B.55° C.45° D.35°
B
3.(1)如图①,O为直线AB上一点,且OC⊥OD,若∠1=25°,则∠2的度数为___________;
65°
(2)如图②,直线AB,CD相交于点O,OE为射线,若∠1=30°,∠2=120°,则OE与AB的位置关系是______________,可记作____________________.
垂直
OE⊥AB
4.过一条线段外一点,作这条线段的垂线,垂足在( )
A.这条线段上 B.这条线段的端点处
C.这条线段的延长线上 D.以上都可以
D
5.下列各图中,过直线l外一点P画l的垂线CD,三角板操作正确的是( )
D
6.(2017·柳州)如图,经过直线l外一点画l的垂线,能画出( )
A.1条 B.2条 C.3条 D.4条
A
7.如图,欲在AB上的某处D点修建一水泵站,将水引到村庄C处,可在图中画出D点,使C,D间铺设的管道最短,这种设计的依据是( )
A.两点之间,线段最短
B.两点确定一条直线
C.垂线段最短
D.过一点有且只有一条直线和已知直线垂直
C
8.如图所示,点P到直线l的距离是( )
A.线段PA的长度
B.线段PB的长度
C.线段PC的长度
D.线段PD的长度
B
9.如图所示,AB⊥AC,AD⊥BC,垂足分别为点A,D,AB=6 cm,AD=5 cm,则点B到直线AC的距离是________,点A到直线BC的距离是__________.
6 cm
5 cm
10.(1)在图①中,过AB外一点M作AB的垂线;
(2)在图②中,过点A,B分别作OB,OA的垂线.
解:(1)如图①所示.
(2)如图②所示.
11.如图,三条直线相交于点O,若CO⊥AB,∠1=56°,则∠2等于( )
A.30° B.34° C.45° D.56°
B
12.(2017·东明县期中)如图,直线a,b相交于点O,OE⊥a于点O,OF⊥b于点O,若∠1=40°,则下列结论正确的是( )
A.∠2=∠3=50°
B.∠2=∠3=40°
C.∠2=40°,∠3=50°
D.∠2=50°,∠3=40°
C
13.如图,AB⊥CD,垂足为点B,EF平分∠ABD,则∠CBF的度数为_________°.
45
14.如图,已知直线CD,EF相交于点O,OA⊥OB,且OE平分∠AOC,若∠EOC=60°,则∠BOF=______________.
30°
15.如图,在直线MN的异侧有A,B两点,按要求画图取点,并注明画图取点的依据.
(1)在直线MN上取一点C,使线段AC最短.依据是_____________________________;
(2)在直线MN上取一点D,使线段AD+BD最短.依据是____________________________.
垂线段最短
两点之间线段最短
解:(1)如图所示,点C即为所求点.
(2)如图所示,点D即为所求点.
16.如图,平原上有A,B,C,D四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池.
(1)不考虑其他因素,请你画图确定蓄水池H点的位置,使它到四个村庄的距离之和最小;
(2)计划把河水引入蓄水池H中,怎样开渠最短?并说明根据.
解:(1)因为两点之间线段最短,所以连接AD,BC交于点H,则H为蓄水池的位置,它到四个村庄的距离之和最小.
(2)过点H作HG⊥EF,垂足为点G.“过直线外一点与直线上各点的连线中,垂线段最短”是把河水引入蓄水池H中开渠最短的根据.
再见
