人教版数学七年级下册5.1.3同位角、内错角、同旁内角 课件(40张)
文档属性
| 名称 | 人教版数学七年级下册5.1.3同位角、内错角、同旁内角 课件(40张) |  | |
| 格式 | pptx | ||
| 文件大小 | 672.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-03 11:26:11 | ||
图片预览



文档简介
人教版 · 数学· 七年级(下)
第5章 相交线与平行线
5.1.3 同位角、内错角、同旁内角
1.理解同位角、内错角、同旁内角的概念。
2.结合图形识别同位角、内错角、同旁内角。
3.从复杂图形分解为基本图形的过程中,体会化繁为简、化难为易的化归思想。
学习目标
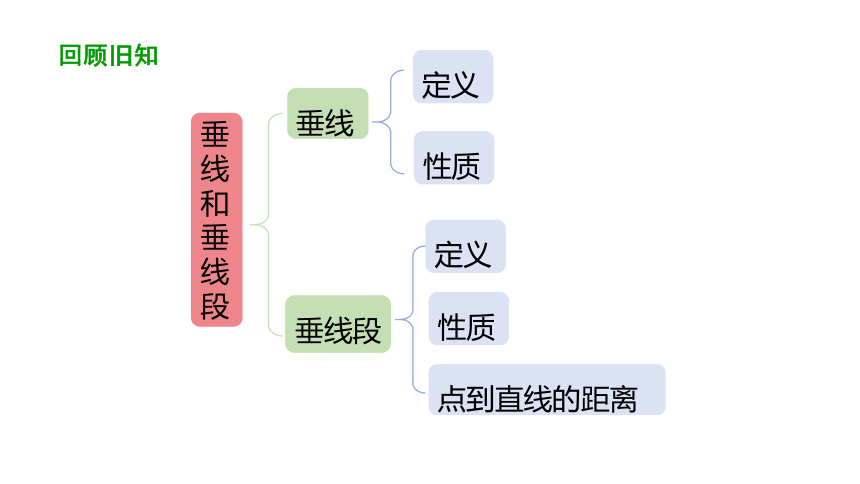
垂线
垂线和垂线段
定义
性质
垂线段
定义
性质
点到直线的距离
回顾旧知
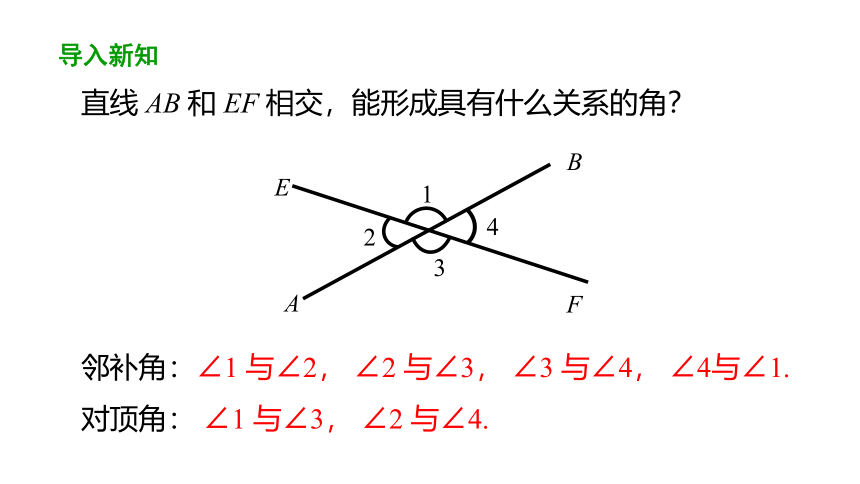
直线 AB 和 EF 相交,能形成具有什么关系的角?
邻补角:∠1 与∠2, ∠2 与∠3, ∠3 与∠4, ∠4与∠1.
对顶角: ∠1 与∠3, ∠2 与∠4.
B
A
F
E
1
4
2
3
导入新知
新知 同位角、内错角、同旁内角
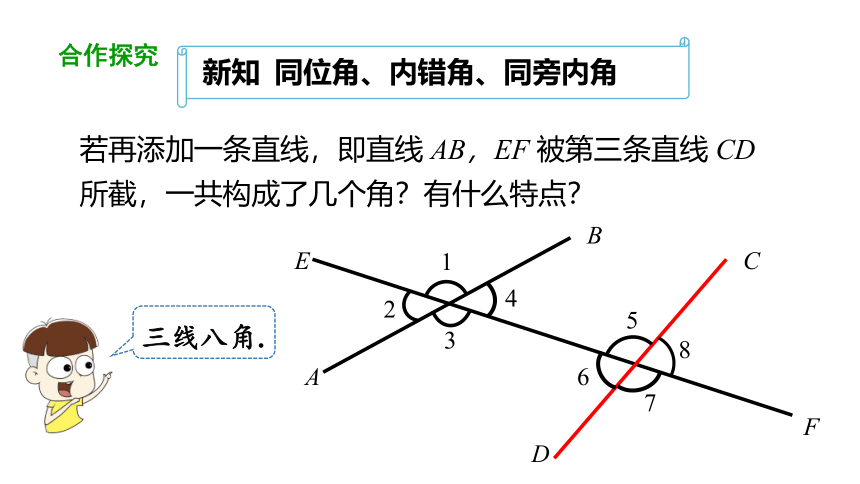
若再添加一条直线,即直线 AB,EF 被第三条直线 CD所截,一共构成了几个角?有什么特点?
5
8
6
7
B
A
F
E
C
D
1
4
2
3
三线八角.
合作探究
F
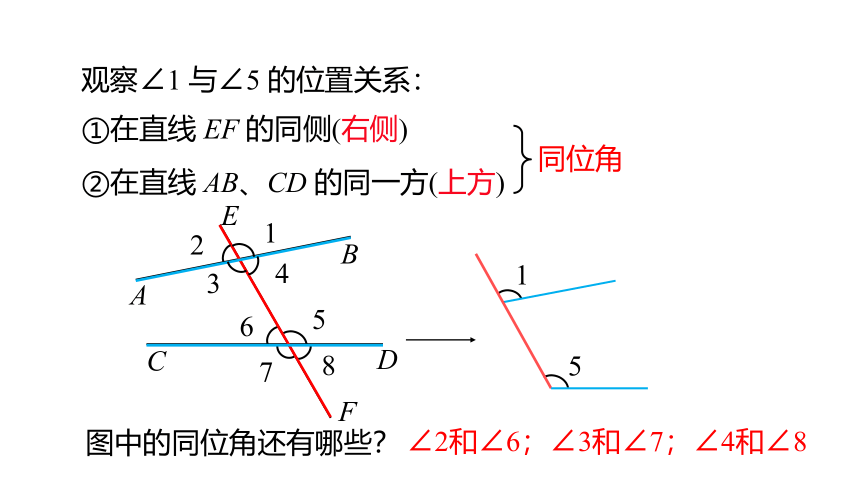
观察∠1 与∠5 的位置关系:
①在直线 EF 的同侧(右侧)
②在直线 AB、CD 的同一方(上方)
A
C
B
D
E
1
2
3
4
5
6
7
8
1
5
∠2和∠6;∠3和∠7;∠4和∠8
图中的同位角还有哪些?
同位角
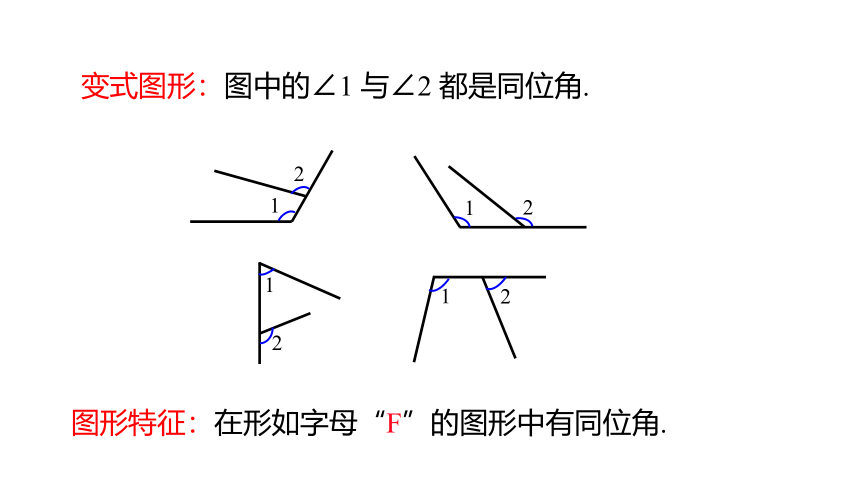
图形特征:在形如字母“F”的图形中有同位角.
变式图形:图中的∠1 与∠2 都是同位角.
1
2
1
2
1
2
1
2
8
A
C
B
D
E
F
1
2
3
4
5
6
7
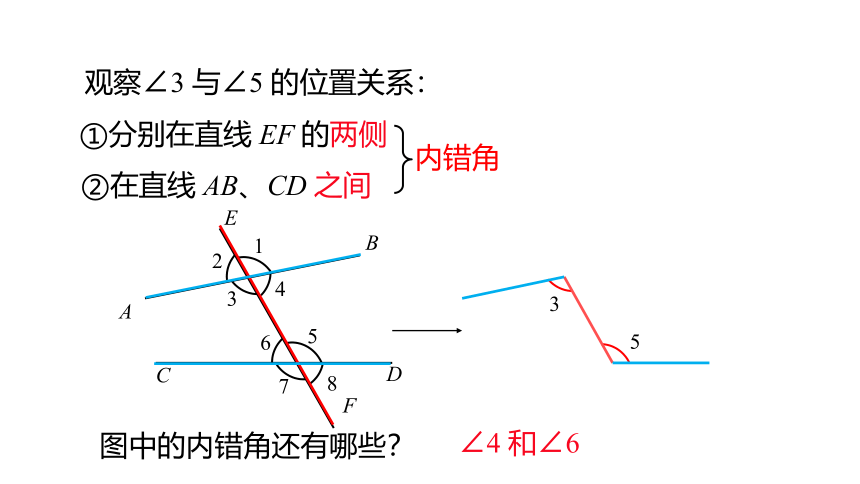
观察∠3 与∠5 的位置关系:
①分别在直线 EF 的两侧
②在直线 AB、CD 之间
3
5
∠4 和∠6
图中的内错角还有哪些?
内错角
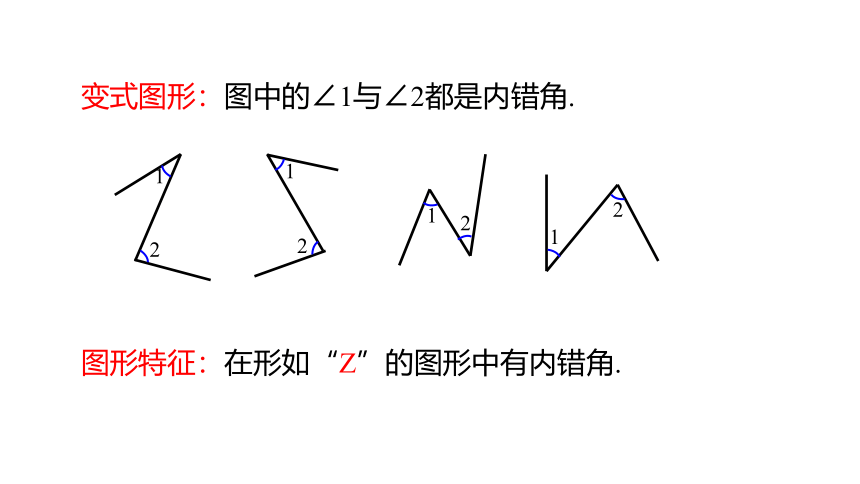
变式图形:图中的∠1与∠2都是内错角.
图形特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
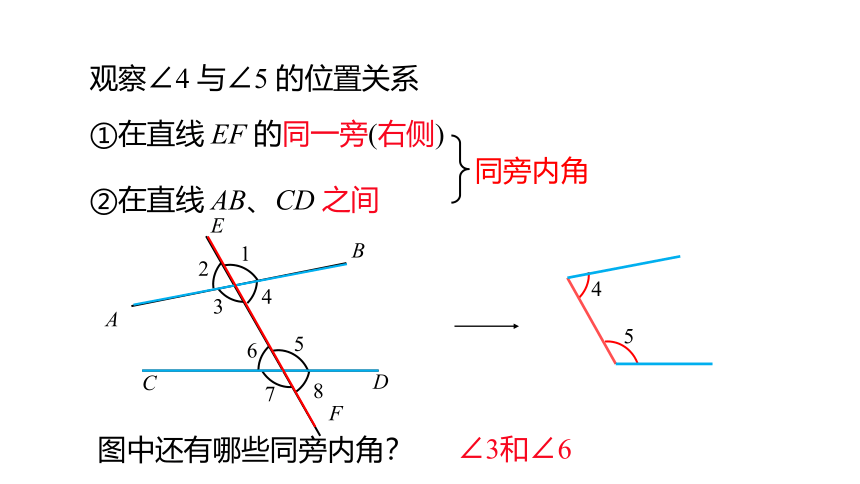
观察∠4 与∠5 的位置关系
①在直线 EF 的同一旁(右侧)
②在直线 AB、CD 之间
4
5
∠3和∠6
图中还有哪些同旁内角?
同旁内角
8
A
C
B
D
E
F
1
2
3
4
5
6
7
变式图形:图中的∠1与∠2都是同旁内角.
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
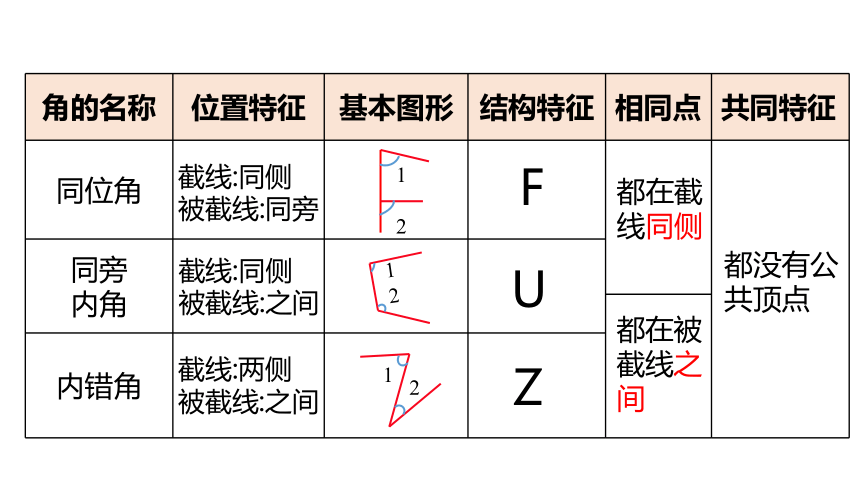
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}角的名称
位置特征
基本图形
结构特征
相同点
共同特征
同位角
同旁
内角
内错角
F
Z
U
截线:同侧
被截线:同旁
截线:同侧
被截线:之间
截线:两侧
被截线:之间
1
2
1
2
1
2
都在截线同侧
都在被截线之间
都没有公共顶点
(1)同位角、内错角、同旁内角都是指两个角之间的位置关系,不是大小关系,它们之间的大小关系都是不确定的.
(2)同位角、内错角、同旁内角都是成对出现的,它们都没有公共顶点,但都有一条边共线.
(3)两条直线被第三条直线所截,构成的八个角中,有四对同位角、两对内错角、两对同旁内角.
把两个角在图中描画出来;
找到两个角的公共直线;
观察所描的角,判断所属“字母”类型,同位角为“F”型,内错角为“Z”型,同旁内角为“U”型,注意图形的变式情况(旋转、对称).
判断三线八角的方法
1
2
3
三线八角手势记忆法
同位角
内错角
同旁内角
例2 如图,直线 DE,BC 被直线 AB 所截.
(1) ∠1 与∠2, ∠1 和∠3,∠1 和∠4 各是什么位置关系的角?
解:(1)∠1与∠2是内错角,
∠1和∠3是同旁内角,
∠1和∠4是同位角.
4
3
2
1
E
D
C
B
A
解:(2)如果∠1 =∠4,由对顶角相等,得∠2 =∠4,
那么∠1 =∠2.
因为∠3 和∠4 互补,即∠4+∠3=180°,
又因为∠1=∠4,
所以∠1+∠3=180°,即∠1与∠3互补.
(2)如果∠1 =∠4,那么∠1 与∠2 相等吗?∠1 与∠3 互补吗? 为什么?
4
3
2
1
E
D
C
B
A
如图,填空:
(1)∠1 和∠B 是直线 , 被直线
所截形成的 角;
(2)∠2 和∠A 是直线 , 被直线
所截形成的 角;
(3)∠B 和∠ECB 是直线 , 被直线 所截形成的 角.
EC
AB
BD
同位
EC
AB
AC
内错
AB
EC
BD
同旁内
巩固新知
“F”型
“Z”型
“U”型
1.同位角、内错角、同旁内角的结构特征:
三线八角
同位角
内错角
同旁内角
归纳新知
2.在图形中判断三线八角的方法(描图法):
①把两个角在图中描画出来;
②找到两个角的公共直线;
③观察所描的角,判断所属“字母”类型,同位角为“F”型,内错角为“Z”型,同旁内角为“U”型,注意图形的变式情况(旋转、对称).
1.下列图中∠1与∠2是同位角的是( )
D
课堂练习
2.如图,∠1与∠2不是同位角的是( )
B
3.同位角的特征是在两条线被截线的____________,并且在截线的__________,如图,∠______和∠_______是同位角.
同一方
同侧
1
2
4.如图,与∠1是内错角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
B
5.如图,∠1的内错角有( )
A.1个 B.2个 C.3个 D.4个
B
6.(2017·钦北区期末)∠1与∠2是内错角,∠1=40°,则( )
A.∠2=40°
B.∠2=140°
C.∠2=40°或∠2=140°
D.∠2的大小不确定
D
7.在我们常见的英文字母中,也存在着同位角、内错角,在下面几个字母中,含有内错角最少的字母是( )
C
8.下列图形中,∠1和∠2是同旁内角的是( )
A
9.如图,∠α的同旁内角的个数有( )
A.1个 B.2个 C.3个 D.4个
C
10.如图所示,下列说法不正确的是( )
A.∠1与∠B是同位角
B.∠1与∠4是内错角
C.∠3与∠B是同旁内角
D.∠C与∠A不是同旁内角
D
11.说出下列各对角分别是哪一条直线截哪两条直线形成的什么角:
(1)∠A和∠ACG; (2)∠ACF和∠CED;
(3)∠AED和∠ACB; (4)∠B和∠BCG.
解:(1)∠A和∠ACG是直线AC截直线CG,AB形成的内错角.
(2)∠ACF和∠CED是直线AC截直线FB,ED形成的内错角.
(3)∠AED和∠ACB是直线AC截直线DE,FB形成的同位角.
(4)∠B和∠BCG是直线FB截直线CG,AB形成的同旁内角.
12.如图,∠1与∠2是( )
A.对顶角
B.同位角
C.内错角
D.同旁内角
B
13.如图,已知直线a,b被直线c所截,那么∠1的同位角是( )
A.∠2
B.∠3
C.∠4
D.∠5
A
14.如图,下列各语句中,错误的语句是( )
A.∠ADE与∠B是同位角
B.∠BDE与∠C是同旁内角
C.∠BDE与∠AED是内错角
D.∠BDE与∠DEC是同旁内角
B
15.在图中,分别找出一个角与α配对,使两个角成为:(1)同位角;(2)内错角;(3)同旁内角,并指出是由哪条直线截另外两条直线而得.
解:(1)∠3,(2)∠1,(3)∠2,直线EF,GH被直线AB所截得的;
或 (1)∠6,(2)∠5,(3)∠4,直线DC,AB被直线GH所截得的.
16.如图,若∠1=∠B,那么∠2与∠B有何数量关系?并说明理由;若∠4+∠C=180°,那么∠3与∠C有何数量关系?并说明理由.
解:∠2+∠B=180°.理由:∵∠1+∠2=180°,∠1=∠B,∴∠2+∠B=180°.
∠3=∠C.理由:∵∠3+∠4=180°,∠4+∠C=180°,∴∠3=∠C.
再见
第5章 相交线与平行线
5.1.3 同位角、内错角、同旁内角
1.理解同位角、内错角、同旁内角的概念。
2.结合图形识别同位角、内错角、同旁内角。
3.从复杂图形分解为基本图形的过程中,体会化繁为简、化难为易的化归思想。
学习目标
垂线
垂线和垂线段
定义
性质
垂线段
定义
性质
点到直线的距离
回顾旧知
直线 AB 和 EF 相交,能形成具有什么关系的角?
邻补角:∠1 与∠2, ∠2 与∠3, ∠3 与∠4, ∠4与∠1.
对顶角: ∠1 与∠3, ∠2 与∠4.
B
A
F
E
1
4
2
3
导入新知
新知 同位角、内错角、同旁内角
若再添加一条直线,即直线 AB,EF 被第三条直线 CD所截,一共构成了几个角?有什么特点?
5
8
6
7
B
A
F
E
C
D
1
4
2
3
三线八角.
合作探究
F
观察∠1 与∠5 的位置关系:
①在直线 EF 的同侧(右侧)
②在直线 AB、CD 的同一方(上方)
A
C
B
D
E
1
2
3
4
5
6
7
8
1
5
∠2和∠6;∠3和∠7;∠4和∠8
图中的同位角还有哪些?
同位角
图形特征:在形如字母“F”的图形中有同位角.
变式图形:图中的∠1 与∠2 都是同位角.
1
2
1
2
1
2
1
2
8
A
C
B
D
E
F
1
2
3
4
5
6
7
观察∠3 与∠5 的位置关系:
①分别在直线 EF 的两侧
②在直线 AB、CD 之间
3
5
∠4 和∠6
图中的内错角还有哪些?
内错角
变式图形:图中的∠1与∠2都是内错角.
图形特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
观察∠4 与∠5 的位置关系
①在直线 EF 的同一旁(右侧)
②在直线 AB、CD 之间
4
5
∠3和∠6
图中还有哪些同旁内角?
同旁内角
8
A
C
B
D
E
F
1
2
3
4
5
6
7
变式图形:图中的∠1与∠2都是同旁内角.
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}角的名称
位置特征
基本图形
结构特征
相同点
共同特征
同位角
同旁
内角
内错角
F
Z
U
截线:同侧
被截线:同旁
截线:同侧
被截线:之间
截线:两侧
被截线:之间
1
2
1
2
1
2
都在截线同侧
都在被截线之间
都没有公共顶点
(1)同位角、内错角、同旁内角都是指两个角之间的位置关系,不是大小关系,它们之间的大小关系都是不确定的.
(2)同位角、内错角、同旁内角都是成对出现的,它们都没有公共顶点,但都有一条边共线.
(3)两条直线被第三条直线所截,构成的八个角中,有四对同位角、两对内错角、两对同旁内角.
把两个角在图中描画出来;
找到两个角的公共直线;
观察所描的角,判断所属“字母”类型,同位角为“F”型,内错角为“Z”型,同旁内角为“U”型,注意图形的变式情况(旋转、对称).
判断三线八角的方法
1
2
3
三线八角手势记忆法
同位角
内错角
同旁内角
例2 如图,直线 DE,BC 被直线 AB 所截.
(1) ∠1 与∠2, ∠1 和∠3,∠1 和∠4 各是什么位置关系的角?
解:(1)∠1与∠2是内错角,
∠1和∠3是同旁内角,
∠1和∠4是同位角.
4
3
2
1
E
D
C
B
A
解:(2)如果∠1 =∠4,由对顶角相等,得∠2 =∠4,
那么∠1 =∠2.
因为∠3 和∠4 互补,即∠4+∠3=180°,
又因为∠1=∠4,
所以∠1+∠3=180°,即∠1与∠3互补.
(2)如果∠1 =∠4,那么∠1 与∠2 相等吗?∠1 与∠3 互补吗? 为什么?
4
3
2
1
E
D
C
B
A
如图,填空:
(1)∠1 和∠B 是直线 , 被直线
所截形成的 角;
(2)∠2 和∠A 是直线 , 被直线
所截形成的 角;
(3)∠B 和∠ECB 是直线 , 被直线 所截形成的 角.
EC
AB
BD
同位
EC
AB
AC
内错
AB
EC
BD
同旁内
巩固新知
“F”型
“Z”型
“U”型
1.同位角、内错角、同旁内角的结构特征:
三线八角
同位角
内错角
同旁内角
归纳新知
2.在图形中判断三线八角的方法(描图法):
①把两个角在图中描画出来;
②找到两个角的公共直线;
③观察所描的角,判断所属“字母”类型,同位角为“F”型,内错角为“Z”型,同旁内角为“U”型,注意图形的变式情况(旋转、对称).
1.下列图中∠1与∠2是同位角的是( )
D
课堂练习
2.如图,∠1与∠2不是同位角的是( )
B
3.同位角的特征是在两条线被截线的____________,并且在截线的__________,如图,∠______和∠_______是同位角.
同一方
同侧
1
2
4.如图,与∠1是内错角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
B
5.如图,∠1的内错角有( )
A.1个 B.2个 C.3个 D.4个
B
6.(2017·钦北区期末)∠1与∠2是内错角,∠1=40°,则( )
A.∠2=40°
B.∠2=140°
C.∠2=40°或∠2=140°
D.∠2的大小不确定
D
7.在我们常见的英文字母中,也存在着同位角、内错角,在下面几个字母中,含有内错角最少的字母是( )
C
8.下列图形中,∠1和∠2是同旁内角的是( )
A
9.如图,∠α的同旁内角的个数有( )
A.1个 B.2个 C.3个 D.4个
C
10.如图所示,下列说法不正确的是( )
A.∠1与∠B是同位角
B.∠1与∠4是内错角
C.∠3与∠B是同旁内角
D.∠C与∠A不是同旁内角
D
11.说出下列各对角分别是哪一条直线截哪两条直线形成的什么角:
(1)∠A和∠ACG; (2)∠ACF和∠CED;
(3)∠AED和∠ACB; (4)∠B和∠BCG.
解:(1)∠A和∠ACG是直线AC截直线CG,AB形成的内错角.
(2)∠ACF和∠CED是直线AC截直线FB,ED形成的内错角.
(3)∠AED和∠ACB是直线AC截直线DE,FB形成的同位角.
(4)∠B和∠BCG是直线FB截直线CG,AB形成的同旁内角.
12.如图,∠1与∠2是( )
A.对顶角
B.同位角
C.内错角
D.同旁内角
B
13.如图,已知直线a,b被直线c所截,那么∠1的同位角是( )
A.∠2
B.∠3
C.∠4
D.∠5
A
14.如图,下列各语句中,错误的语句是( )
A.∠ADE与∠B是同位角
B.∠BDE与∠C是同旁内角
C.∠BDE与∠AED是内错角
D.∠BDE与∠DEC是同旁内角
B
15.在图中,分别找出一个角与α配对,使两个角成为:(1)同位角;(2)内错角;(3)同旁内角,并指出是由哪条直线截另外两条直线而得.
解:(1)∠3,(2)∠1,(3)∠2,直线EF,GH被直线AB所截得的;
或 (1)∠6,(2)∠5,(3)∠4,直线DC,AB被直线GH所截得的.
16.如图,若∠1=∠B,那么∠2与∠B有何数量关系?并说明理由;若∠4+∠C=180°,那么∠3与∠C有何数量关系?并说明理由.
解:∠2+∠B=180°.理由:∵∠1+∠2=180°,∠1=∠B,∴∠2+∠B=180°.
∠3=∠C.理由:∵∠3+∠4=180°,∠4+∠C=180°,∴∠3=∠C.
再见
