6.2排列与组合 课堂讲义-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(机构适用)(含答案)
文档属性
| 名称 | 6.2排列与组合 课堂讲义-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(机构适用)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 240.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 17:24:48 | ||
图片预览



文档简介
6.2排列与组合
1、排列与排列数公式
从n个不同元素中,任取m(m≤n)个元素(这里的被取元素各不相同)按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列。
注意:(1)排列定义包含两个基本内容:一是“取出元素”,二是“按照一定顺序”排列。
(2)定义中“一定顺序”就是说与位置有关,在实际问题中,要由具体问题的性质和条件决定,这一点是与组合的根本区别。
2、排列数
从n个不同元素中取出m(m≤n)个元素排成一列,称为从n个不同元素中取出m个元素的一个排列.从n个不同元素中取出m个元素的一个排列数,用符号 表示。排列数公式:
注意:我们把正整数由1到n的连乘积,叫做n的阶乘,用n!表示。规定0!=1。
当m=n时,n个不同元素全部取出的一个排列,叫做n个不同元素的一个全排列,记为false
3、组合
从n个不同的元素中任取m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.
注意:(1)取出的m个元素不讲究顺序,也就是说元素没有位置的要求,无序性是组合的本质。
(2)组合与排列的异同:组合与排列的相同点是“从n个不同元素中任意取出m个不同元素”;不同点是组合“不管元素的顺序并成一组”,而排列要求元素“按照一定的顺序排成一列”,因此区分某一问题是组合还是排列,关键是看取出的元素有无顺序。
4、组合数与组合数公式
从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号表示。组合数公式:
false或falsefalse
规定:=1。
5、组合数的两个性质
性质1:false
一般地,从n个不同元素中取出false个元素后,剩下false个元素.因为从n个不同元素中取出m个元素的每一个组合,与剩下的n m个元素的每一个组合一一对应,所以从n个不同元素中取出m个元素的组合数,等于从这n个元素中取出n m个元素的组合数,即:false.在这里,主要体现:“取法”与“剩法”是“一一对应”的思想
注意:(1)该性质反映了组合数的对称性。
(2)若m>,通常不直接计算,而改为计算。
性质2:false=false+false
一般地,从false这n+1个不同元素中取出m个元素的组合数是false,这些组合可以分为两类:一类含有元素false,一类不含有false.含有false的组合是从false这n个元素中取出m 1个元素与false组成的,共有false个;不含有false的组合是从false这n个元素中取出m个元素组成的,共有false个.根据分类计数原理,可以得到组合数的另一个性质.在这里,主要体现从特殊到一般的归纳思想,“含与不含其元素”的分类思想.
例1.用数字1,2,3,4,6可以组成无重复数字的五位偶数有( )
A.48个 B.64个
C.72个 D.90个
【答案】C
【详解】
满足条件的五位偶数有:false.
故选:C.
例2.用数字0,1,2,3,4,5组成没有重复数字且大于201345的正整数有( )个.
A.478 B.479 C.480 D.481
【答案】B
【详解】
由以1开头的没有重复数字的六位数的个数为false,由于201345是以2开头的没有重复数字的六位数中最小的一个,所有的没有重复数字的六位数的个数为false
故没有重复数字且大于201345的六位数的个数为false,
故选:B.
1.false年false月false日,国家航天局探月与航天工程中心组织完成了我国首辆火星车全球征名活动的初次评审.初评环节遴选出弘毅、麒麟、哪吒、赤兔、祝融、求索、风火轮、追梦、天行、星火共false个名称,作为我国首辆火星车的命名范围.某同学为了研究这些初选名字的内涵,计划从中随机选取false个依次进行分析,若同时选中哪吒、赤兔,则哪吒和赤兔连续被分析,否则随机依次分析,则所有不同的分析情况有( )
A.false种 B.false种 C.false种 D.false种
2.某校学生志愿者服务团队由3名男同学和2名女同学组成,若从这5名同学中随机选出3人参加社区志愿者活动,且每人被选到的可能性相等,则恰有2名男同学被选中的概率为( )
A.false B.false C.false D.false
3.在假期里,有5名同学去社区做防疫志愿者,根据需要,要安排这5名同学去甲、乙两个核酸检测点,每个检测点至少去2名同学,则不同的安排方法共有( )
A.10种 B.20种 C.24种 D.30种
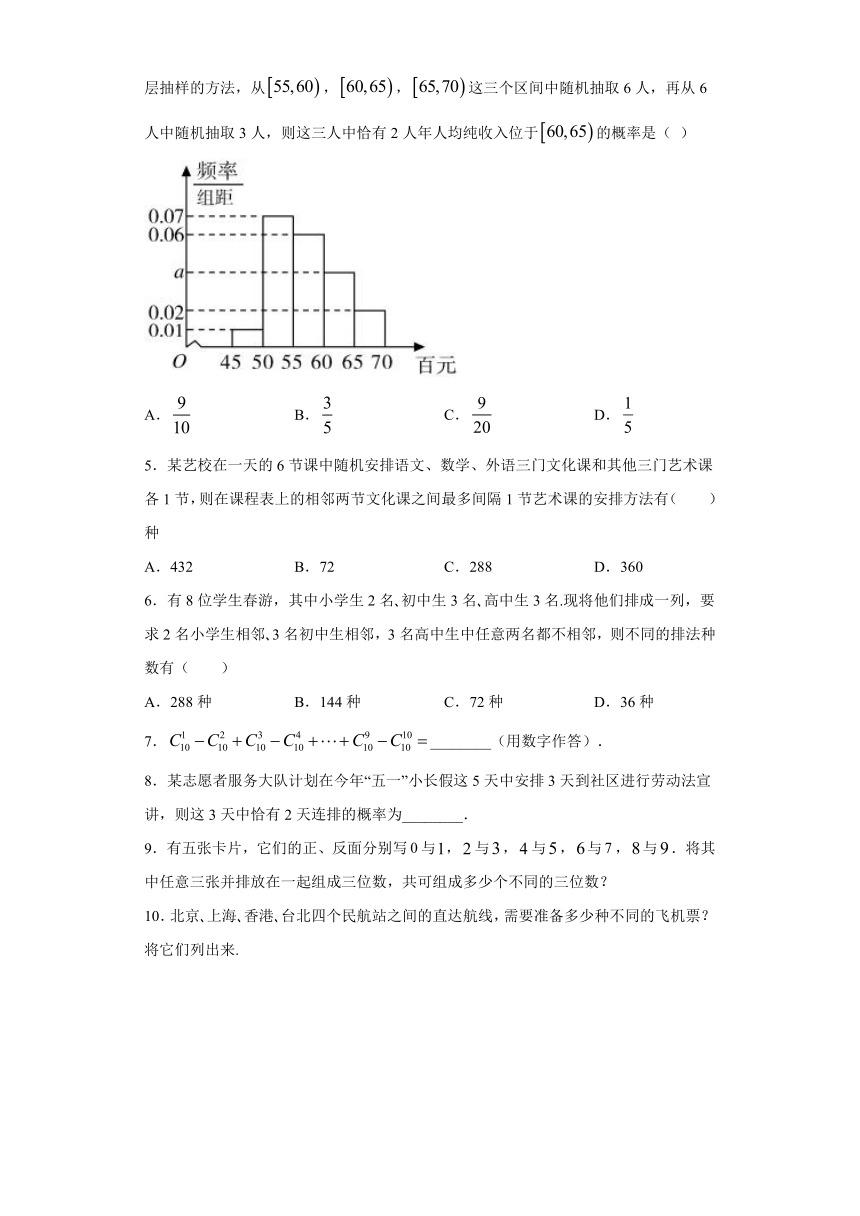
4.为了解某贫困地区实施精准扶贫后的成果,现随机抽取了该地区部分人员,调查了2020年其人均纯收入状况.经统计,这批人员的年人均纯收入数据(单位:百元)全部介于45至70之间.将数据分成5组,并得到如图所示的频率分布直方图.现采取分层抽样的方法,从false,false,false这三个区间中随机抽取6人,再从6人中随机抽取3人,则这三人中恰有2人年人均纯收入位于false的概率是( )
A.false B.false C.false D.false
5.某艺校在一天的6节课中随机安排语文、数学、外语三门文化课和其他三门艺术课各1节,则在课程表上的相邻两节文化课之间最多间隔1节艺术课的安排方法有( )种
A.432 B.72 C.288 D.360
6.有8位学生春游,其中小学生2名?初中生3名?高中生3名.现将他们排成一列,要求2名小学生相邻?3名初中生相邻,3名高中生中任意两名都不相邻,则不同的排法种数有( )
A.288种 B.144种 C.72种 D.36种
7.false________(用数字作答).
8.某志愿者服务大队计划在今年“五一”小长假这5天中安排3天到社区进行劳动法宣讲,则这3天中恰有2天连排的概率为________.
9.有五张卡片,它们的正、反面分别写false与false,false与false,false与false,false与false,false与false.将其中任意三张并排放在一起组成三位数,共可组成多少个不同的三位数?
10.北京?上海?香港?台北四个民航站之间的直达航线,需要准备多少种不同的飞机票?将它们列出来.
---------------------------------------------------------------参考答案------------------------------------------------------------
1.A
【详解】
①同时选中哪吒和赤兔,则只需从剩余的false个初选名字中选出false个,再进行排列即可,有false种情况;
②哪吒和赤兔有一个入选,则需从剩余的false个初选名字中选出false个,再进行排列,有false种情况;
③哪吒和赤兔都不选,则需从剩余的false个初选名字中选出false个,再进行排列,有false种情况;
false不同的分析情况共有false种.
故选:A.
2.D
【详解】
由题意知:恰有2名男同学被选中的选法有false种,而总选法有false种,
∴恰有2名男同学被选中的概率为false.
故选:D.
3.B
【详解】
根据题意,分2步进行分析:
①将5人分为2组,每组至少2人,所以只能分为2和3的两组,有false种方法;
②将分好的2组全排列,安排到2个社区,有false种情况,
则共有false种不同的安排方法.
故选:B.
4.D
【详解】
由图可知false,解得:false,
false的频率为false,false的频率为false,false的频率为false,则对应的频率之比为false,
则false组抽3人,false抽取2人,false抽取1人,
则6人中随机抽取3人,则这三人中恰有2人年人均纯收入位于false的概率是false.
故选:D
5.A
【详解】
把语文、数学、外语三门文化课排列,有false种方法,
这三门课中间存在两个空,在两个空中,
①若每个空各插入1节艺术课,则排法种数为false,
②若两个空中只插入1节艺术课,则排法种数为false,
③若语文、数学、外语三门文化课相邻排列,把三门文化课捆绑为一个整体,
然后和三门艺术课进行排列,则排法种数为false,
相邻两节文化课之间最多间隔1节艺术课的安排方法有false,
故选:A.
6.B
【详解】
第一步,先将2名小学生看成一个人,3名初中生看成一个人,然后排成一排有false种不同排法;第二步,将3名高中生插在这两个整体形成的3个空档中,有false种不同排法;第三步,排2名小学生有false种不同排法,排3名初中生有false种不同排法.
根据分步计数原理,共有false种不同排法.
故选:B
7.1
【详解】
false=false
=10-45+120-210+252-210+12—45+10-1=1
8.false
【详解】
由题意,由插空法得3天中恰有2天连排的概率为false,
故答案为false.
9.false个
【详解】
(1)取false不取false,则先从另四张卡片中选一张作百位,有正反两种可能,有false种;false可从后两位中任选一个位置,有false种;最后从剩余的三张卡片中任选一张,有正反两种可能,有false种;
false取false不取false共可组成false个不同的三位数;
(2)取false不取false,则从四张卡片中任选两张,每张都有正反两种可能,有false种;与false搭配构成三位数有false种排法;
false取false不取false共可组成false个不同的三位数;
(3)false和false都不取,则从四张卡片中任选三张,每张都有正反两种可能,有false种;三个数字搭配构成三位数有false种排法;
falsefalse和false都不取共可组成false个不同的三位数;
综上所述:共可组成false个不同的三位数.
10.12(种),列举答案见解析.
【详解】
每两个民航站之间的直达航线有往返两种不同的飞机票,
所以四个民航站之间的直达航线,需要准备false种不同的飞机票.
列举如下:
北京false上海,北京false香港,北京false台北,
上海false北京,上海false香港,上海false台北,
香港false北京,香港false上海,香港false台北,
台北false北京,台北false上海,台北false香港.
1、排列与排列数公式
从n个不同元素中,任取m(m≤n)个元素(这里的被取元素各不相同)按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列。
注意:(1)排列定义包含两个基本内容:一是“取出元素”,二是“按照一定顺序”排列。
(2)定义中“一定顺序”就是说与位置有关,在实际问题中,要由具体问题的性质和条件决定,这一点是与组合的根本区别。
2、排列数
从n个不同元素中取出m(m≤n)个元素排成一列,称为从n个不同元素中取出m个元素的一个排列.从n个不同元素中取出m个元素的一个排列数,用符号 表示。排列数公式:
注意:我们把正整数由1到n的连乘积,叫做n的阶乘,用n!表示。规定0!=1。
当m=n时,n个不同元素全部取出的一个排列,叫做n个不同元素的一个全排列,记为false
3、组合
从n个不同的元素中任取m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.
注意:(1)取出的m个元素不讲究顺序,也就是说元素没有位置的要求,无序性是组合的本质。
(2)组合与排列的异同:组合与排列的相同点是“从n个不同元素中任意取出m个不同元素”;不同点是组合“不管元素的顺序并成一组”,而排列要求元素“按照一定的顺序排成一列”,因此区分某一问题是组合还是排列,关键是看取出的元素有无顺序。
4、组合数与组合数公式
从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号表示。组合数公式:
false或falsefalse
规定:=1。
5、组合数的两个性质
性质1:false
一般地,从n个不同元素中取出false个元素后,剩下false个元素.因为从n个不同元素中取出m个元素的每一个组合,与剩下的n m个元素的每一个组合一一对应,所以从n个不同元素中取出m个元素的组合数,等于从这n个元素中取出n m个元素的组合数,即:false.在这里,主要体现:“取法”与“剩法”是“一一对应”的思想
注意:(1)该性质反映了组合数的对称性。
(2)若m>,通常不直接计算,而改为计算。
性质2:false=false+false
一般地,从false这n+1个不同元素中取出m个元素的组合数是false,这些组合可以分为两类:一类含有元素false,一类不含有false.含有false的组合是从false这n个元素中取出m 1个元素与false组成的,共有false个;不含有false的组合是从false这n个元素中取出m个元素组成的,共有false个.根据分类计数原理,可以得到组合数的另一个性质.在这里,主要体现从特殊到一般的归纳思想,“含与不含其元素”的分类思想.
例1.用数字1,2,3,4,6可以组成无重复数字的五位偶数有( )
A.48个 B.64个
C.72个 D.90个
【答案】C
【详解】
满足条件的五位偶数有:false.
故选:C.
例2.用数字0,1,2,3,4,5组成没有重复数字且大于201345的正整数有( )个.
A.478 B.479 C.480 D.481
【答案】B
【详解】
由以1开头的没有重复数字的六位数的个数为false,由于201345是以2开头的没有重复数字的六位数中最小的一个,所有的没有重复数字的六位数的个数为false
故没有重复数字且大于201345的六位数的个数为false,
故选:B.
1.false年false月false日,国家航天局探月与航天工程中心组织完成了我国首辆火星车全球征名活动的初次评审.初评环节遴选出弘毅、麒麟、哪吒、赤兔、祝融、求索、风火轮、追梦、天行、星火共false个名称,作为我国首辆火星车的命名范围.某同学为了研究这些初选名字的内涵,计划从中随机选取false个依次进行分析,若同时选中哪吒、赤兔,则哪吒和赤兔连续被分析,否则随机依次分析,则所有不同的分析情况有( )
A.false种 B.false种 C.false种 D.false种
2.某校学生志愿者服务团队由3名男同学和2名女同学组成,若从这5名同学中随机选出3人参加社区志愿者活动,且每人被选到的可能性相等,则恰有2名男同学被选中的概率为( )
A.false B.false C.false D.false
3.在假期里,有5名同学去社区做防疫志愿者,根据需要,要安排这5名同学去甲、乙两个核酸检测点,每个检测点至少去2名同学,则不同的安排方法共有( )
A.10种 B.20种 C.24种 D.30种
4.为了解某贫困地区实施精准扶贫后的成果,现随机抽取了该地区部分人员,调查了2020年其人均纯收入状况.经统计,这批人员的年人均纯收入数据(单位:百元)全部介于45至70之间.将数据分成5组,并得到如图所示的频率分布直方图.现采取分层抽样的方法,从false,false,false这三个区间中随机抽取6人,再从6人中随机抽取3人,则这三人中恰有2人年人均纯收入位于false的概率是( )
A.false B.false C.false D.false
5.某艺校在一天的6节课中随机安排语文、数学、外语三门文化课和其他三门艺术课各1节,则在课程表上的相邻两节文化课之间最多间隔1节艺术课的安排方法有( )种
A.432 B.72 C.288 D.360
6.有8位学生春游,其中小学生2名?初中生3名?高中生3名.现将他们排成一列,要求2名小学生相邻?3名初中生相邻,3名高中生中任意两名都不相邻,则不同的排法种数有( )
A.288种 B.144种 C.72种 D.36种
7.false________(用数字作答).
8.某志愿者服务大队计划在今年“五一”小长假这5天中安排3天到社区进行劳动法宣讲,则这3天中恰有2天连排的概率为________.
9.有五张卡片,它们的正、反面分别写false与false,false与false,false与false,false与false,false与false.将其中任意三张并排放在一起组成三位数,共可组成多少个不同的三位数?
10.北京?上海?香港?台北四个民航站之间的直达航线,需要准备多少种不同的飞机票?将它们列出来.
---------------------------------------------------------------参考答案------------------------------------------------------------
1.A
【详解】
①同时选中哪吒和赤兔,则只需从剩余的false个初选名字中选出false个,再进行排列即可,有false种情况;
②哪吒和赤兔有一个入选,则需从剩余的false个初选名字中选出false个,再进行排列,有false种情况;
③哪吒和赤兔都不选,则需从剩余的false个初选名字中选出false个,再进行排列,有false种情况;
false不同的分析情况共有false种.
故选:A.
2.D
【详解】
由题意知:恰有2名男同学被选中的选法有false种,而总选法有false种,
∴恰有2名男同学被选中的概率为false.
故选:D.
3.B
【详解】
根据题意,分2步进行分析:
①将5人分为2组,每组至少2人,所以只能分为2和3的两组,有false种方法;
②将分好的2组全排列,安排到2个社区,有false种情况,
则共有false种不同的安排方法.
故选:B.
4.D
【详解】
由图可知false,解得:false,
false的频率为false,false的频率为false,false的频率为false,则对应的频率之比为false,
则false组抽3人,false抽取2人,false抽取1人,
则6人中随机抽取3人,则这三人中恰有2人年人均纯收入位于false的概率是false.
故选:D
5.A
【详解】
把语文、数学、外语三门文化课排列,有false种方法,
这三门课中间存在两个空,在两个空中,
①若每个空各插入1节艺术课,则排法种数为false,
②若两个空中只插入1节艺术课,则排法种数为false,
③若语文、数学、外语三门文化课相邻排列,把三门文化课捆绑为一个整体,
然后和三门艺术课进行排列,则排法种数为false,
相邻两节文化课之间最多间隔1节艺术课的安排方法有false,
故选:A.
6.B
【详解】
第一步,先将2名小学生看成一个人,3名初中生看成一个人,然后排成一排有false种不同排法;第二步,将3名高中生插在这两个整体形成的3个空档中,有false种不同排法;第三步,排2名小学生有false种不同排法,排3名初中生有false种不同排法.
根据分步计数原理,共有false种不同排法.
故选:B
7.1
【详解】
false=false
=10-45+120-210+252-210+12—45+10-1=1
8.false
【详解】
由题意,由插空法得3天中恰有2天连排的概率为false,
故答案为false.
9.false个
【详解】
(1)取false不取false,则先从另四张卡片中选一张作百位,有正反两种可能,有false种;false可从后两位中任选一个位置,有false种;最后从剩余的三张卡片中任选一张,有正反两种可能,有false种;
false取false不取false共可组成false个不同的三位数;
(2)取false不取false,则从四张卡片中任选两张,每张都有正反两种可能,有false种;与false搭配构成三位数有false种排法;
false取false不取false共可组成false个不同的三位数;
(3)false和false都不取,则从四张卡片中任选三张,每张都有正反两种可能,有false种;三个数字搭配构成三位数有false种排法;
falsefalse和false都不取共可组成false个不同的三位数;
综上所述:共可组成false个不同的三位数.
10.12(种),列举答案见解析.
【详解】
每两个民航站之间的直达航线有往返两种不同的飞机票,
所以四个民航站之间的直达航线,需要准备false种不同的飞机票.
列举如下:
北京false上海,北京false香港,北京false台北,
上海false北京,上海false香港,上海false台北,
香港false北京,香港false上海,香港false台北,
台北false北京,台北false上海,台北false香港.
