7.4二项分布与超几何分布 课堂讲义-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(机构适用)(含答案)
文档属性
| 名称 | 7.4二项分布与超几何分布 课堂讲义-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(机构适用)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 323.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 17:28:02 | ||
图片预览




文档简介
7.4二项分布与超几何分布
1.关键是判断超几何分布与二项分布
判断一个随机变量是否服从超几何分布,关键是要看随机变量是否满足超几何分布的特征:一个总体(共有个)内含有两种不同的事物、,任取个,其中恰有个.符合该条件的即可断定是超几何分布,按照超几何分布的分布列()进行处理就可以了.
2.二项分布必须同时满足以下两个条件:①在一次试验中试验结果只有与这两个,且事件发生的概率为,事件发生的概率为;②试验可以独立重复地进行,即每次重复做一次试验,事件发生的概率都是同一常数,事件发生的概率为.
1.若随机变量false,且false,false,则false( )
A.false B.false C.false D.false
2.一个袋子中有4个黑球和1个白球,从中取一球,取后放回,重复n次,记取出的球为白球的次数为X,若false,则false( )
A.60 B.false C.false D.12
3.某同学参加学校篮球选修课的期末考试,老师规定每个同学罚篮20次,每罚进一球得5分,不进记0分,已知该同学罚球命中率为60%,则该同学得分的数学期望和方差分别为( ).
A.60,24 B.80,120 C.80,24 D.60,120
4.已知随机变量false服从二项分布false,则false.
A.false B.false C.false D.false
5.设false,则false等于
A.1.6 B.3.2 C.6.4 D.12.8
6.已知X~B(n,p),EX=8,DX=1.6,则n与p的值分别是( )
A.100,0.08 B.20,0.4 C.10,0.2 D.10,0.8
7.已知随机变量false,若false,则false的值等于__________.
8.设随机变量ξ服从二项分布false,则函数f(x)=x2+4x+ξ存在零点的概率是________.
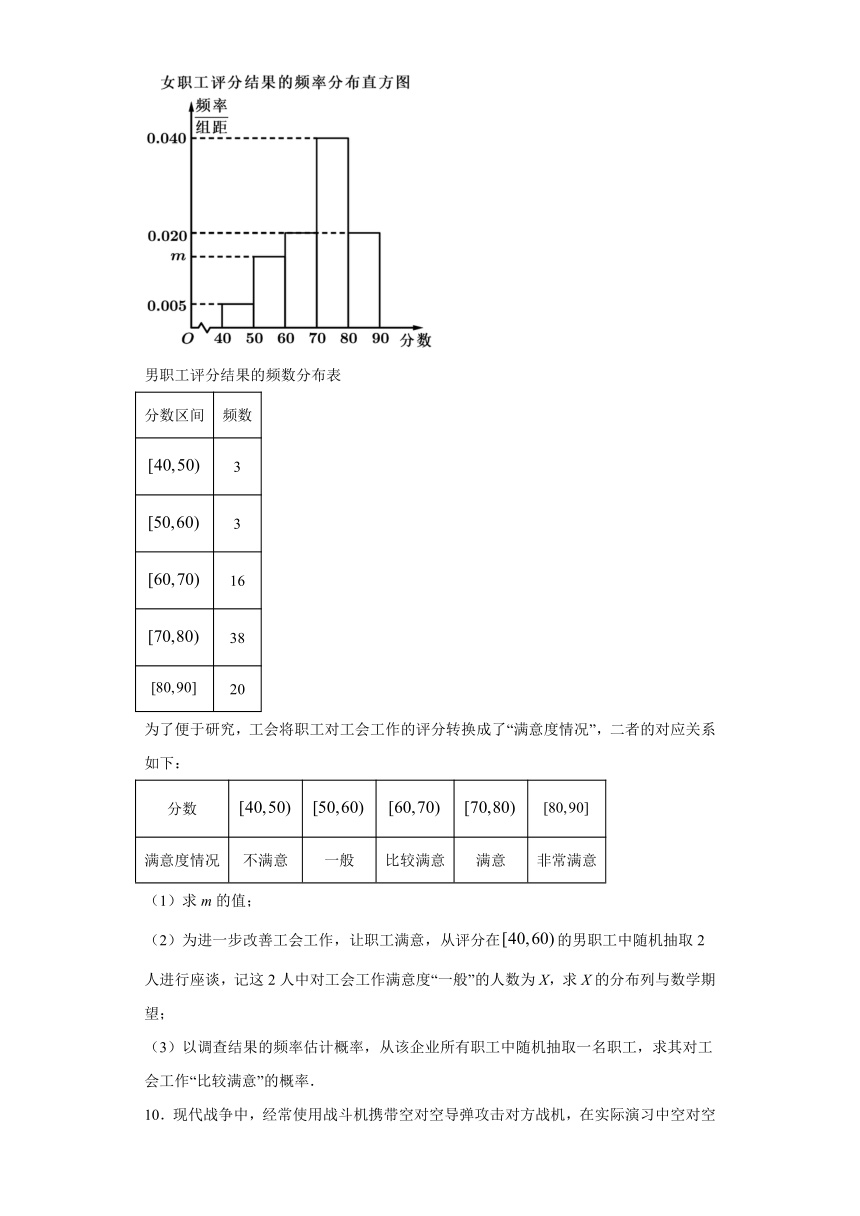
9.为了解企业职工对工会工作满意度情况之间的关系,某企业工会按性别采用分层抽样的方法,从全体企业职工中抽取容量为200的样本进行调查.被抽中的职工分别对工会工作进行评分,满分为100分,调查结果显示:最低分为40分,最高分为90分.随后,企业工会将男、女职工的评分结果按照相同的分组方式分别整理成了频数分布表和频率分布直方图,图表如下:
男职工评分结果的频数分布表
分数区间
频数
false
3
false
3
false
16
false
38
false
20
为了便于研究,工会将职工对工会工作的评分转换成了“满意度情况”,二者的对应关系如下:
分数
false
false
false
false
false
满意度情况
不满意
一般
比较满意
满意
非常满意
(1)求m的值;
(2)为进一步改善工会工作,让职工满意,从评分在false的男职工中随机抽取2人进行座谈,记这2人中对工会工作满意度“一般”的人数为X,求X的分布列与数学期望;
(3)以调查结果的频率估计概率,从该企业所有职工中随机抽取一名职工,求其对工会工作“比较满意”的概率.
10.现代战争中,经常使用战斗机携带空对空导弹攻击对方战机,在实际演习中空对空导弹的命中率约为20%,由于飞行员的综合素质和经验的不同,不同的飞行员使用空对空导弹命中对方战机的概率也不尽相同.在一次演习中,红方的甲?乙两名优秀飞行员发射一枚空对空导弹命中蓝方战机的概率分别为false和false,两名飞行员各携带4枚空对空导弹.
(1)甲飞行员单独攻击蓝方一架战机,连续不断地发射导弹攻击,一旦命中或导弹用完即停止攻击,各次攻击相互独立,求甲飞行员能够命中蓝方战机的概率?
(2)蓝方机群共有8架战机,若甲?乙共同攻击(战机均在攻击范围之内,每枚导弹只攻击其中一架战机,甲,乙不同时攻击同一架战机).
①若一轮攻击中,每人只有两次进攻机会,记一轮攻击中,击中蓝方战机数为X,求X的分布列;
②若实施两轮攻击(用完携带的导弹),记命中蓝方战机数为Y,求Y的数学期望E(Y).
1.若随机变量false,且false,false,则false( )
A.false B.false C.false D.false
2.一个袋子中有4个黑球和1个白球,从中取一球,取后放回,重复n次,记取出的球为白球的次数为X,若false,则false( )
A.60 B.false C.false D.12
3.某同学参加学校篮球选修课的期末考试,老师规定每个同学罚篮20次,每罚进一球得5分,不进记0分,已知该同学罚球命中率为60%,则该同学得分的数学期望和方差分别为( ).
A.60,24 B.80,120 C.80,24 D.60,120
4.已知随机变量false服从二项分布false,则false.
A.false B.false C.false D.false
5.设false,则false等于
A.1.6 B.3.2 C.6.4 D.12.8
6.已知X~B(n,p),EX=8,DX=1.6,则n与p的值分别是( )
A.100,0.08 B.20,0.4 C.10,0.2 D.10,0.8
7.已知随机变量false,若false,则false的值等于__________.
8.设随机变量ξ服从二项分布false,则函数f(x)=x2+4x+ξ存在零点的概率是________.
9.为了解企业职工对工会工作满意度情况之间的关系,某企业工会按性别采用分层抽样的方法,从全体企业职工中抽取容量为200的样本进行调查.被抽中的职工分别对工会工作进行评分,满分为100分,调查结果显示:最低分为40分,最高分为90分.随后,企业工会将男、女职工的评分结果按照相同的分组方式分别整理成了频数分布表和频率分布直方图,图表如下:
男职工评分结果的频数分布表
分数区间
频数
false
3
false
3
false
16
false
38
false
20
为了便于研究,工会将职工对工会工作的评分转换成了“满意度情况”,二者的对应关系如下:
分数
false
false
false
false
false
满意度情况
不满意
一般
比较满意
满意
非常满意
(1)求m的值;
(2)为进一步改善工会工作,让职工满意,从评分在false的男职工中随机抽取2人进行座谈,记这2人中对工会工作满意度“一般”的人数为X,求X的分布列与数学期望;
(3)以调查结果的频率估计概率,从该企业所有职工中随机抽取一名职工,求其对工会工作“比较满意”的概率.
10.现代战争中,经常使用战斗机携带空对空导弹攻击对方战机,在实际演习中空对空导弹的命中率约为20%,由于飞行员的综合素质和经验的不同,不同的飞行员使用空对空导弹命中对方战机的概率也不尽相同.在一次演习中,红方的甲?乙两名优秀飞行员发射一枚空对空导弹命中蓝方战机的概率分别为false和false,两名飞行员各携带4枚空对空导弹.
(1)甲飞行员单独攻击蓝方一架战机,连续不断地发射导弹攻击,一旦命中或导弹用完即停止攻击,各次攻击相互独立,求甲飞行员能够命中蓝方战机的概率?
(2)蓝方机群共有8架战机,若甲?乙共同攻击(战机均在攻击范围之内,每枚导弹只攻击其中一架战机,甲,乙不同时攻击同一架战机).
①若一轮攻击中,每人只有两次进攻机会,记一轮攻击中,击中蓝方战机数为X,求X的分布列;
②若实施两轮攻击(用完携带的导弹),记命中蓝方战机数为Y,求Y的数学期望E(Y).
---------------------------------------------------------------参考答案------------------------------------------------------------
1.A
【详解】
解:因为随机变量false,且false,false,
所以false,解得false,
故选:A
2.A
【详解】
由题意可知false,
false,false,
false,
false.
3.D
【详解】
设该同学false次罚篮,命中次数为false,则false,
所以false,false,
所以该同学得分false的期望为false,
方差为false.
故选:D
4.D
【详解】
false表示做了false次独立实验,每次试验成功概率为false,
则false.选false.
5.C
6.D
【详解】
由题意知false,且false,
则false,解得false,故选D.
7.false
【详解】
false,解得false(false舍去),false.
故答案为:false.
8.false
【详解】
由函数f(x)=x2+4x+ξ存在零点,得Δ=16-4ξ≥0,即ξ≤4.又因为变量ξ~Bfalse,
所以所求概率false .
故答案为:false.
9.(1)false;(2)分布列见解析,1;(3)false.
【详解】
解:(1)因为false,
所以false.
(2)依题意,随机变量X的所有可能取值为0,1,2.
则false,false,
false.
所以随机变量X的分布列为
X
0
1
2
P
false
false
false
故X的数学期望false.
(3)设事件false{随机抽取一名职工,对工会工作服务“比较满意”}.
因为样本人数200人,其中男职工共有80人,
所以样本中女职工共有120人.
由频率分布直方图可知,
女职工对工会工作服务“比较满意”的人数共有:false人.
由频数分布表,可知男职工对工会工作“比较满意”的共有16人,
所以随机抽取一名职工,对工会工作“比较满意”的概率为false.
10.(1)false;(2)①分布列答案见解析;②false.
【详解】
解:设甲?乙两名飞行员发射的第i枚导弹命中对方战机分别为事件false,则false,false.
(1)设甲飞行员能够击中蓝方战机为事件M,则false,
所以false
false
false
false.
(2)①false,则
false,
false,
false,
false,
false,
所以X的分布列为
X
0
1
2
3
4
P
false
false
false
false
false
②记两轮攻击中甲命中战机数为false,则false,乙命中战机数为false,则false,
所以false.
1.关键是判断超几何分布与二项分布
判断一个随机变量是否服从超几何分布,关键是要看随机变量是否满足超几何分布的特征:一个总体(共有个)内含有两种不同的事物、,任取个,其中恰有个.符合该条件的即可断定是超几何分布,按照超几何分布的分布列()进行处理就可以了.
2.二项分布必须同时满足以下两个条件:①在一次试验中试验结果只有与这两个,且事件发生的概率为,事件发生的概率为;②试验可以独立重复地进行,即每次重复做一次试验,事件发生的概率都是同一常数,事件发生的概率为.
1.若随机变量false,且false,false,则false( )
A.false B.false C.false D.false
2.一个袋子中有4个黑球和1个白球,从中取一球,取后放回,重复n次,记取出的球为白球的次数为X,若false,则false( )
A.60 B.false C.false D.12
3.某同学参加学校篮球选修课的期末考试,老师规定每个同学罚篮20次,每罚进一球得5分,不进记0分,已知该同学罚球命中率为60%,则该同学得分的数学期望和方差分别为( ).
A.60,24 B.80,120 C.80,24 D.60,120
4.已知随机变量false服从二项分布false,则false.
A.false B.false C.false D.false
5.设false,则false等于
A.1.6 B.3.2 C.6.4 D.12.8
6.已知X~B(n,p),EX=8,DX=1.6,则n与p的值分别是( )
A.100,0.08 B.20,0.4 C.10,0.2 D.10,0.8
7.已知随机变量false,若false,则false的值等于__________.
8.设随机变量ξ服从二项分布false,则函数f(x)=x2+4x+ξ存在零点的概率是________.
9.为了解企业职工对工会工作满意度情况之间的关系,某企业工会按性别采用分层抽样的方法,从全体企业职工中抽取容量为200的样本进行调查.被抽中的职工分别对工会工作进行评分,满分为100分,调查结果显示:最低分为40分,最高分为90分.随后,企业工会将男、女职工的评分结果按照相同的分组方式分别整理成了频数分布表和频率分布直方图,图表如下:
男职工评分结果的频数分布表
分数区间
频数
false
3
false
3
false
16
false
38
false
20
为了便于研究,工会将职工对工会工作的评分转换成了“满意度情况”,二者的对应关系如下:
分数
false
false
false
false
false
满意度情况
不满意
一般
比较满意
满意
非常满意
(1)求m的值;
(2)为进一步改善工会工作,让职工满意,从评分在false的男职工中随机抽取2人进行座谈,记这2人中对工会工作满意度“一般”的人数为X,求X的分布列与数学期望;
(3)以调查结果的频率估计概率,从该企业所有职工中随机抽取一名职工,求其对工会工作“比较满意”的概率.
10.现代战争中,经常使用战斗机携带空对空导弹攻击对方战机,在实际演习中空对空导弹的命中率约为20%,由于飞行员的综合素质和经验的不同,不同的飞行员使用空对空导弹命中对方战机的概率也不尽相同.在一次演习中,红方的甲?乙两名优秀飞行员发射一枚空对空导弹命中蓝方战机的概率分别为false和false,两名飞行员各携带4枚空对空导弹.
(1)甲飞行员单独攻击蓝方一架战机,连续不断地发射导弹攻击,一旦命中或导弹用完即停止攻击,各次攻击相互独立,求甲飞行员能够命中蓝方战机的概率?
(2)蓝方机群共有8架战机,若甲?乙共同攻击(战机均在攻击范围之内,每枚导弹只攻击其中一架战机,甲,乙不同时攻击同一架战机).
①若一轮攻击中,每人只有两次进攻机会,记一轮攻击中,击中蓝方战机数为X,求X的分布列;
②若实施两轮攻击(用完携带的导弹),记命中蓝方战机数为Y,求Y的数学期望E(Y).
1.若随机变量false,且false,false,则false( )
A.false B.false C.false D.false
2.一个袋子中有4个黑球和1个白球,从中取一球,取后放回,重复n次,记取出的球为白球的次数为X,若false,则false( )
A.60 B.false C.false D.12
3.某同学参加学校篮球选修课的期末考试,老师规定每个同学罚篮20次,每罚进一球得5分,不进记0分,已知该同学罚球命中率为60%,则该同学得分的数学期望和方差分别为( ).
A.60,24 B.80,120 C.80,24 D.60,120
4.已知随机变量false服从二项分布false,则false.
A.false B.false C.false D.false
5.设false,则false等于
A.1.6 B.3.2 C.6.4 D.12.8
6.已知X~B(n,p),EX=8,DX=1.6,则n与p的值分别是( )
A.100,0.08 B.20,0.4 C.10,0.2 D.10,0.8
7.已知随机变量false,若false,则false的值等于__________.
8.设随机变量ξ服从二项分布false,则函数f(x)=x2+4x+ξ存在零点的概率是________.
9.为了解企业职工对工会工作满意度情况之间的关系,某企业工会按性别采用分层抽样的方法,从全体企业职工中抽取容量为200的样本进行调查.被抽中的职工分别对工会工作进行评分,满分为100分,调查结果显示:最低分为40分,最高分为90分.随后,企业工会将男、女职工的评分结果按照相同的分组方式分别整理成了频数分布表和频率分布直方图,图表如下:
男职工评分结果的频数分布表
分数区间
频数
false
3
false
3
false
16
false
38
false
20
为了便于研究,工会将职工对工会工作的评分转换成了“满意度情况”,二者的对应关系如下:
分数
false
false
false
false
false
满意度情况
不满意
一般
比较满意
满意
非常满意
(1)求m的值;
(2)为进一步改善工会工作,让职工满意,从评分在false的男职工中随机抽取2人进行座谈,记这2人中对工会工作满意度“一般”的人数为X,求X的分布列与数学期望;
(3)以调查结果的频率估计概率,从该企业所有职工中随机抽取一名职工,求其对工会工作“比较满意”的概率.
10.现代战争中,经常使用战斗机携带空对空导弹攻击对方战机,在实际演习中空对空导弹的命中率约为20%,由于飞行员的综合素质和经验的不同,不同的飞行员使用空对空导弹命中对方战机的概率也不尽相同.在一次演习中,红方的甲?乙两名优秀飞行员发射一枚空对空导弹命中蓝方战机的概率分别为false和false,两名飞行员各携带4枚空对空导弹.
(1)甲飞行员单独攻击蓝方一架战机,连续不断地发射导弹攻击,一旦命中或导弹用完即停止攻击,各次攻击相互独立,求甲飞行员能够命中蓝方战机的概率?
(2)蓝方机群共有8架战机,若甲?乙共同攻击(战机均在攻击范围之内,每枚导弹只攻击其中一架战机,甲,乙不同时攻击同一架战机).
①若一轮攻击中,每人只有两次进攻机会,记一轮攻击中,击中蓝方战机数为X,求X的分布列;
②若实施两轮攻击(用完携带的导弹),记命中蓝方战机数为Y,求Y的数学期望E(Y).
---------------------------------------------------------------参考答案------------------------------------------------------------
1.A
【详解】
解:因为随机变量false,且false,false,
所以false,解得false,
故选:A
2.A
【详解】
由题意可知false,
false,false,
false,
false.
3.D
【详解】
设该同学false次罚篮,命中次数为false,则false,
所以false,false,
所以该同学得分false的期望为false,
方差为false.
故选:D
4.D
【详解】
false表示做了false次独立实验,每次试验成功概率为false,
则false.选false.
5.C
6.D
【详解】
由题意知false,且false,
则false,解得false,故选D.
7.false
【详解】
false,解得false(false舍去),false.
故答案为:false.
8.false
【详解】
由函数f(x)=x2+4x+ξ存在零点,得Δ=16-4ξ≥0,即ξ≤4.又因为变量ξ~Bfalse,
所以所求概率false .
故答案为:false.
9.(1)false;(2)分布列见解析,1;(3)false.
【详解】
解:(1)因为false,
所以false.
(2)依题意,随机变量X的所有可能取值为0,1,2.
则false,false,
false.
所以随机变量X的分布列为
X
0
1
2
P
false
false
false
故X的数学期望false.
(3)设事件false{随机抽取一名职工,对工会工作服务“比较满意”}.
因为样本人数200人,其中男职工共有80人,
所以样本中女职工共有120人.
由频率分布直方图可知,
女职工对工会工作服务“比较满意”的人数共有:false人.
由频数分布表,可知男职工对工会工作“比较满意”的共有16人,
所以随机抽取一名职工,对工会工作“比较满意”的概率为false.
10.(1)false;(2)①分布列答案见解析;②false.
【详解】
解:设甲?乙两名飞行员发射的第i枚导弹命中对方战机分别为事件false,则false,false.
(1)设甲飞行员能够击中蓝方战机为事件M,则false,
所以false
false
false
false.
(2)①false,则
false,
false,
false,
false,
false,
所以X的分布列为
X
0
1
2
3
4
P
false
false
false
false
false
②记两轮攻击中甲命中战机数为false,则false,乙命中战机数为false,则false,
所以false.
