第9章 统计 单元测试B卷-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册(Word含解析)
文档属性
| 名称 | 第9章 统计 单元测试B卷-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册(Word含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 281.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 00:00:00 | ||
图片预览


文档简介
2020—2021学年高一数学下学期第九章单元测试卷
满分: 100分 时间: 60分钟
第Ⅰ卷(选择题 共60分)
单项选择题:本题共12小题,每题只有一个选项正确,每小题5分,共计60分。
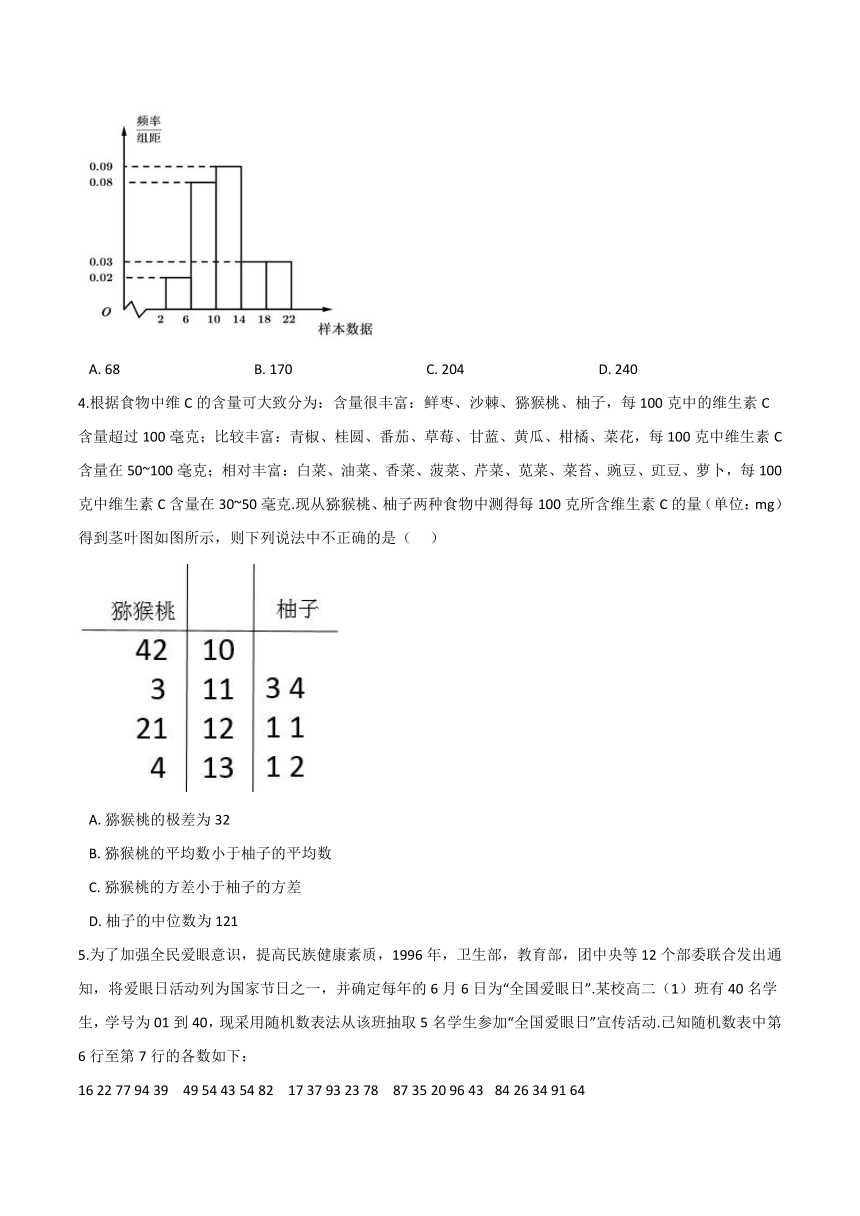
1.2021年我国推进新冠疫苗全人群免费接种,某小区年龄分布如下图所示,现用分层抽样的方法从该小区所有人中抽取60人进行抗体检测,则从40岁至50岁之间的人群中抽取人数为(??? ).
A.?18??????????????????????????????????????????B.?24??????????????????????????????????????????C.?5??????????????????????????????????????????D.?9
2.某学校组建了演讲,舞蹈?航模?合唱,机器人五个社团,全校 3000 名学生每人都参加且只参加其中一个社团,校团委从这 3000 名学生中随机选取部分学生进行调查,并将调查结果绘制了如下不完整的两个统计图:
则选取的学生中参加机器人社团的学生数为(??? )
A.?50???????????????????????????????????????B.?75???????????????????????????????????????C.?100???????????????????????????????????????D.?125
3.如图,是统计某样本数据得到的频率分布直方图,已知该样本容量为300,则样本数据落在 [6,14) 内的频数为(??? )
A.?68???????????????????????????????????????B.?170???????????????????????????????????????C.?204???????????????????????????????????????D.?240
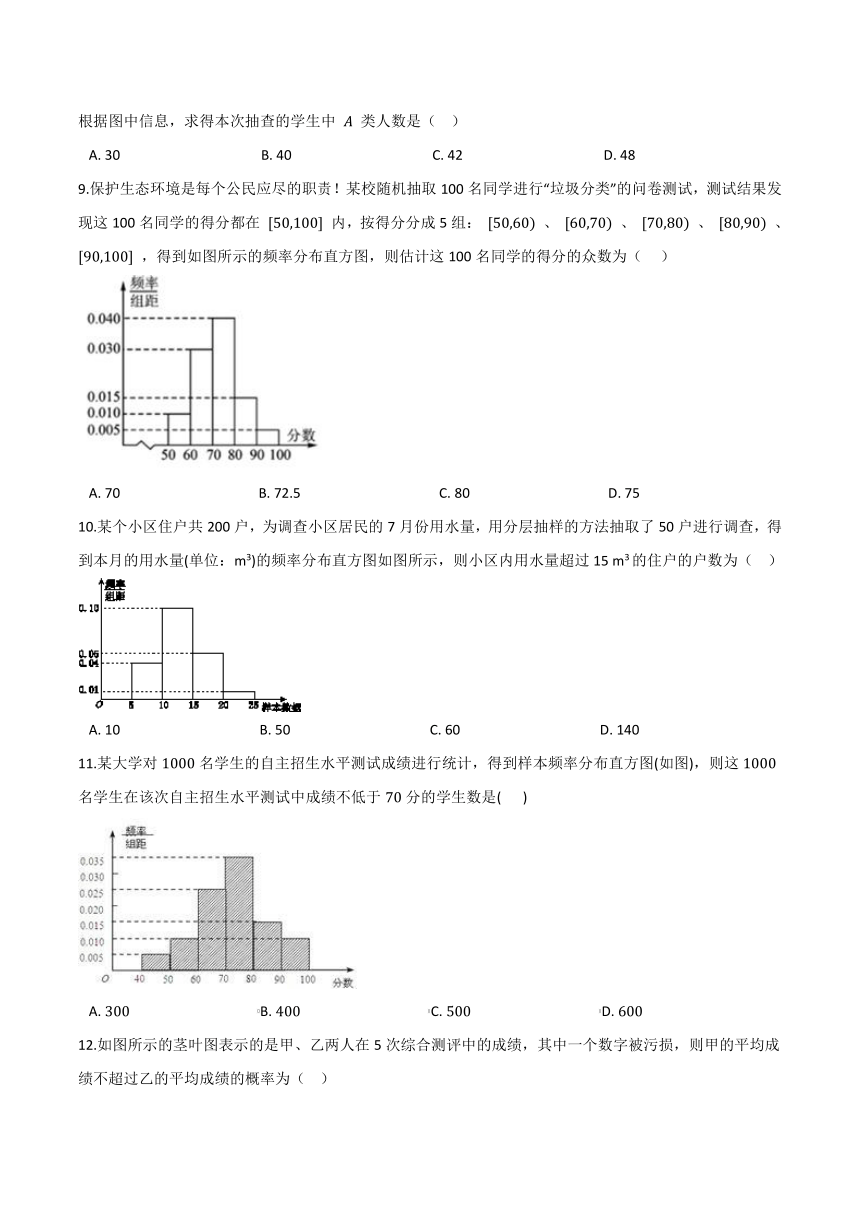
4.根据食物中维C的含量可大致分为:含量很丰富:鲜枣、沙棘、猕猴桃、柚子,每100克中的维生素C含量超过100毫克;比较丰富:青椒、桂圆、番茄、草莓、甘蓝、黄瓜、柑橘、菜花,每100克中维生素C含量在50~100毫克;相对丰富:白菜、油菜、香菜、菠菜、芹菜、苋菜、菜苔、豌豆、豇豆、萝卜,每100克中维生素C含量在30~50毫克.现从猕猴桃、柚子两种食物中测得每100克所含维生素C的量(单位:mg)得到茎叶图如图所示,则下列说法中不正确的是(??? )
A.?猕猴桃的极差为32
B.?猕猴桃的平均数小于柚子的平均数
C.?猕猴桃的方差小于柚子的方差
D.?柚子的中位数为121
5.为了加强全民爱眼意识,提高民族健康素质,1996年,卫生部,教育部,团中央等12个部委联合发出通知,将爱眼日活动列为国家节日之一,并确定每年的6月6日为“全国爱眼日”.某校高二(1)班有40名学生,学号为01到40,现采用随机数表法从该班抽取5名学生参加“全国爱眼日”宣传活动.已知随机数表中第6行至第7行的各数如下:
16 22 77 94 39?? 49 54 43 54 82?? 17 37 93 23 78?? 87 35 20 96 43? 84 26 34 91 64
84 42 17 53 31?? 57 24 55 06 88?? 77 04 74 47 67?? 21 76 33 50 25? 83 92 12 06 76
若从随机数表第6行第9列的数开始向右读则抽取的第5名学生的学号是(??? )
A.?17?????????????????????????????????????????B.?23?????????????????????????????????????????C.?35?????????????????????????????????????????D.?37
6.某中学初中部有600名学生,高中部有800名学生,其性别比例如图所示,则该校男生比女生多(? ?)
A.?60人??????????????????????????????????B.?100人??????????????????????????????????C.?150人??????????????????????????????????D.?180人
7.某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业者岗位分布条形图,则下列结论中不正确的是(? )
注:90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生.
A.?互联网行业从业人员中90后占一半以上
B.?互联网行业中从事技术岗位的人数超过总人数的20%
C.?互联网行业中从事产品岗位的90后人数超过总人数的5%
D.?互联网行业中从事运营岗位的90后人数比80前人数多
8.某学校为了了解本校学生的上学方式,在全校范围内随机抽查部分学生,了解到上学方式主要有: A ——结伴步行, B ——自行乘车, C ——家人接送, D ——其他方式,并将收集的数据整理绘制成如下两幅不完整的统计图.
根据图中信息,求得本次抽查的学生中 A 类人数是(?? )
A.?30?????????????????????????????????????????B.?40?????????????????????????????????????????C.?42?????????????????????????????????????????D.?48
9.保护生态环境是每个公民应尽的职责!某校随机抽取100名同学进行“垃圾分类”的问卷测试,测试结果发现这100名同学的得分都在 [50,100] 内,按得分分成5组: [50,60) 、 [60,70) 、 [70,80) 、 [80,90) 、 [90,100] ,得到如图所示的频率分布直方图,则估计这100名同学的得分的众数为(??? )
A.?70????????????????????????????????????????B.?72.5????????????????????????????????????????C.?80????????????????????????????????????????D.?75
10.某个小区住户共200户,为调查小区居民的7月份用水量,用分层抽样的方法抽取了50户进行调查,得到本月的用水量(单位:m3)的频率分布直方图如图所示,则小区内用水量超过15 m3的住户的户数为(?? )
A.?10????????????????????????????????????????B.?50????????????????????????????????????????C.?60????????????????????????????????????????D.?140
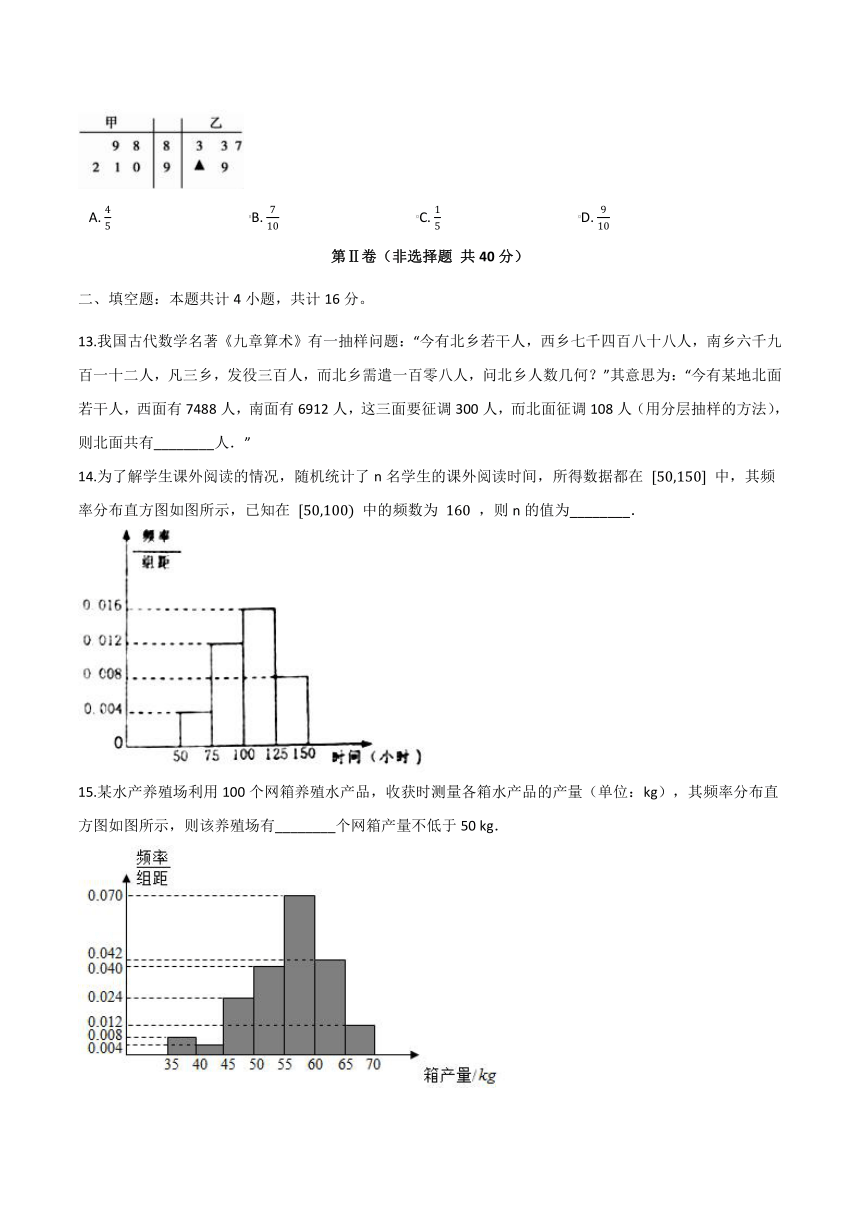
11.某大学对1000名学生的自主招生水平测试成绩进行统计,得到样本频率分布直方图(如图),则这1000名学生在该次自主招生水平测试中成绩不低于70分的学生数是(???? )
A.?300?????????????????????????????????????B.?400?????????????????????????????????????C.?500?????????????????????????????????????D.?600
12.如图所示的茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩不超过乙的平均成绩的概率为(?? )
A.?45????????????????????????????????????????B.?710????????????????????????????????????????C.?15????????????????????????????????????????D.?910
第Ⅱ卷(非选择题 共40分)
二、填空题:本题共计4小题,共计16分。
13.我国古代数学名著《九章算术》有一抽样问题:“今有北乡若干人,西乡七千四百八十八人,南乡六千九百一十二人,凡三乡,发役三百人,而北乡需遣一百零八人,问北乡人数几何?”其意思为:“今有某地北面若干人,西面有7488人,南面有6912人,这三面要征调300人,而北面征调108人(用分层抽样的方法),则北面共有________人.”
14.为了解学生课外阅读的情况,随机统计了n名学生的课外阅读时间,所得数据都在 [50,150] 中,其频率分布直方图如图所示,已知在 [50,100) 中的频数为 160 ,则n的值为________.
15.某水产养殖场利用100个网箱养殖水产品,收获时测量各箱水产品的产量(单位:kg),其频率分布直方图如图所示,则该养殖场有________个网箱产量不低于50 kg.
16.在某批次的某种灯泡中,随机抽取200个样品.并对其寿命进行追踪调查,将结果列成频率分布表如下:
寿命(天)
频数
频率
[200,300)
40
a
[300,400)
60
0.3
[400,500)
b
0.4
[500,600)
20
0.1
合计
200
1
某人从灯泡样品中随机地购买了 n(n∈N?) 个,如果这 n 个灯泡的寿命情况恰好与按四个组分层抽样所得的结果相同,则 n 的最小值为________.
三、解答题:本题共计4小题,共计24分。
17.为了推进分级诊疗,实现“基层首诊?双向转诊?急慢分治?上下联动”的诊疗模式,某城市自2020年起全面推行家庭医生签约服务.已知该城市居民约为1000万,从0岁到100岁的居民年龄结构的频率分布直方图如图1所示.为了解各年龄段居民签约家庭医生的情况,现调查了1000名年满18周岁的居民,各年龄段被访者签约率如图2所示.
(1)估计该城市年龄在50岁以上且已签约家庭医生的居民人数;
(2)据统计,该城市被访者的签约率约为44%.为把该城市年满18周岁居民的签约率提高到55%以上,应着重提高图2中哪个年龄段的签约率?并根据已有数据陈述理由.
18.为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成A,B两组,每组100只,其中A组小鼠给服甲离子溶液,B组小鼠给服乙离子溶液,每只小鼠给服的溶液体积相同、摩尔浓度相同。经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
记C为事件:“乙离子残留在体内的百分比不低于5.5”,根据直方图得到P(C)的估计值为0.70.
(1)求乙离子残留百分比直方图中a,b的值;
(2)分别估计甲,乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表)
19.? 2019年2月13日《烟台市全民阅读促进条例》全文发布,旨在保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设.某高校为了解条例发布以来全校学生的阅读情况,随机调查了200名学生每周阅读时间 X (单位:小时)并绘制如图所示的频率分布直方图.
(1)求这200名学生每周阅读时间的样本平均数 x 和中位数 a ( a 的值精确到0.01);
(2)为查找影响学生阅读时间的因素,学校团委决定从每周阅读时间为 [6.5,7.5) , [7.5,8.5) 的学生中抽取9名参加座谈会.
(i)你认为9个名额应该怎么分配?并说明理由;
(ii)座谈中发现9名学生中理工类专业的较多.请根据200名学生的调研数据,填写下面的列联表,并判断是否有 95% 的把握认为学生阅读时间不足(每周阅读时间不足8.5小时)与“是否理工类专业”有关?
阅读时间不足8.5小时
阅读时间超过8.5小时
理工类专业
40
60
非理工类专业
附: K2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d) ( n=a+b+c+d ).
临界值表:
P(K2≥k0)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.072
2.706
3.841
5.024
6.635
7.879
10.828
20.2020年5月28日,十三届全国人大三次会议表决通过了《中华人民共和国民法典》,此法典被称为“社会生活的百科全书”,是新中国第一部以法典命名的法律,在法律体系中居于基础性地位,也是市场经济的基本法.民法典与百姓生活密切相关,某学校有800名学生,为了解学生对民法典的认识程度,选取了100名学生进行测试,制成如图所示频率分布直方图.
(1)求m的值;
(2)估计抽查学生测试成绩的中位数;(结果用分数形式表示)
(3)如果抽查的测试平均分超过75分,就表示该学校通过测试,试判断该校能否通过测试.
答案解析
一、单选题
1.【答案】 A
【解析】由条形统计图的数据,根据分层抽样的定义可以知道,
若抽取60人,则从40岁至50岁之间的人群中抽取人数为 60×300200+400+300+100=18 .
故答案为:A.
2.【答案】 B
【解析】由题意,本次调查的人数为 50÷10%=500 人,
其中合唱比赛所占的比例为 200500=0.4=40% ,
所以机器人所占的比例为 1?10%?20%?15%?40%=15%. ,
所以选取的学生中参加机器人社团的学生数为 500×15%=75 人.
故答案为:B.
3.【答案】 C
【解析】样本数据落在 [6,14) 内的频率为 (0.08+0.09)×4=0.68 ,
所以样本数据落在 [6,14) 内的频数为 300×0.68=204 ,
故答案为:C
4.【答案】 C
【解析】解:对于 A ,猕猴桃的极差为: 134?102=32 ,故 A 正确;
对于 B ,猕猴桃的平均数是 x=16(104+102+113+121+122+134)=116 ,
柚子的平均数是 y=16(113+114+121+121+131+132)=122 ,故 B 正确;
对于 C ,猕猴桃的方差是: s12=16(196+144+9+25+36+324)=12213 ,
柚子的方差是: s22=16(81+64+1+1+81+100)=54.67 ,
故猕猴桃的方差大于柚子的方差,故 C 错误;
对于 D ,柚子的中位数是121,故 D 正确;
故答案为:C.
5.【答案】 C
【解析】解:读取的前5名学生的学号依次是:39,17,37,23,35,
故答案为:C.
6.【答案】 B
【解析】解:由题意可得,初中部男生人数为 600×45%=270 ,女生人数为 600?270=330 ;高中部女生人数为 800×40%=320 ,男生人数为 800?320=480 .故该校男生比女生多 480+270?320?330=100 人.
故答案为:B
7.【答案】 C
【解析】A选项,由图可知90后占了56%,故正确;
B选项,互联网行业中90后从事技术岗位中所占比例为 0.56×39.6%=0.22176>0.2 ,互联网行业中从事技术岗位的人数还包括80后,80前,所以互联网行业中从事技术岗位的人数超过总人数的20%,是肯定的,故正确;
C选项,互联网行业中从事产品岗位的90后人数所占比例为 0.56×6.5%=0.0364<0.05 ,故不正确;
D选项,互联网行业中从事运营岗位的90后人数所占比例为 0.56×0.17=0.0952>0.03 ,故正确.
故答案为:C.
8.【答案】 A
【解析】解:根据选择D方式的有18人,所占比例为15%,得总人数为 1815%= 120人,故选择A方式的人数为120﹣42﹣30﹣18=30人.
故答案为:A.
9.【答案】 D
【解析】由频率分布直方图可知,这 100 名同学的得分的众数为 70+802=75 .
故答案为:D.
10.【答案】 C
【解析】从频率分布直方图可知,用水量超过15m?的住户的频率为 (0.05+0.01)×5=0.3 ,即分层抽样的50户中有0.3×50=15户住户的用水量超过15立方米所以小区内用水量超过15立方米的住户户数为 1550×200=60 ,故答案为:C
11.【答案】 D
【解析】该次自主招生水平测试中成绩不低于70分的学生数==?故选D.
12.【答案】 C
【解析】解:由茎叶图知甲的平均成绩为 15 ×(88+89+90+91+92)=90,
∵甲的平均成绩不超过乙的平均成绩,
∴设被污损为x,则乙的平均成绩为 15 ×(83+83+87+99+90+x)≥90,
解得x≥8,
∴甲的平均成绩不超过乙的平均成绩的概率为P= 210=15 .
故答案为:C.
二、填空题
13.【答案】 8100
【解析】因为共抽调300人,北面抽掉了108人,所以西面和南面共14400人中抽出了192人,所以抽样比为 19214400 ,所以北面共有 108×14400192=8100 人,故填8100。
14.【答案】 400
【解析】由频率分布直方图得: [50,100) 的频率为: (0.004+0.012)×25=0.4 ,
∵ 在 [50,100) 中的频数为 160 , ∴n=1600.4=400 .
故答案为: 400 .
15.【答案】 82
【解析】由频率分布直方图,可知不低于50kg的频率为:(0.040+0.070+0.042+0.012)×5=0.82,
所以网箱个数:0.082×100=82.
16.【答案】 10
【解析】由题意得,a=0.2,b=80,由表可知,灯泡样品第一组有40个,第二组有60个,第三组有80个,第四组有20个,所以四个组的比例为2:3:4:1,所以按分层抽样法,购买的灯泡数为n=2k+3k+4k+k =10k( k∈N? ),所以 n 的最小值为10.
三、解答题
17.【答案】 (1)解:该城市年龄在50-60岁的签约人数为: 1000×0.015×10×55.7%=83.55 万;
在60-70岁的签约人数为: 1000×0.010×10×61.7%=61.7 万;
在70-80岁的签约人数为: 1000×0.004×10×70.0%=28 万;
在80岁以上的签约人数为: 1000×0.003×10×75.8%=22.74 万;
故该城市年龄在50岁以上且已签约家庭医生的居民人数为: 83.55+61.7+28+22.74=199.55 万;
(2)解:年龄在10-20岁的人数为: 1000×0.005×10=50 万;
年龄在20-30岁的人数为: 1000×0.018×10=180 万.
所以,年龄在18-30岁的人数大于180万,小于230万,签约率为30.3%;
年龄在30-50岁的人数为 1000×0.037×10=370 万,签约率为37.1%.
年龄在50岁以上的人数为: 1000×0.032×10=320 万,签约率超过55%,上升空间不大.
故由以上数据可知这个城市在30-50岁这个年龄段的人数为370万,基数较其他年龄段是最大的,且签约率非常低,所以为把该地区满18周岁居民的签约率提高到以上,应着重提高30-50这个年龄段的签约率.
【解析】(1)根据题中频率分布直方图与各年龄段被访者的签约率,分别计算50岁以上各年龄段的居民人数,再求和,即可得出结果;
(2)根据题中条件,先确定年龄在18-30岁的人数,年龄在30-50岁的人数,以及年龄在50岁以上的人数,即可确定结果。
18.【答案】 (1)解:由已知得0.70=a+0.20+0.15,故a=0.35.
b=1–0.05–0.15–0.70=0.10.
(2)甲离子残留百分比的平均值的估计值为
2×0.15+3×0.20+4×0.30+5×0.20+6×0.10+7×0.05=4.05.
乙离子残留百分比的平均值的估计值为
3×0.05+4×0.10+5×0.15+6×0.35+7×0.20+8×0.15=6.00.
【解析】(1)由已知利用频率分布直方图,百分比不低于5.5的估计值为0.70列式,即可求出a,b的值;(2)由频率分布直方图平均数的计算公式,利用区间的中点值为代表列式,即可求出平均值.
19.【答案】 (1)解:该组数据的平均数 x=6×0.03+7×0.1+8×0.2+9×0.35+10×0.19 +11×0.09+12×0.04=9 ,
因为 0.03+0.1+0.2+0.35=0.68>0.5 ,所以中位数 a∈[8.5,9.5) ,
由 0.03+0.1+0.2+(a?8.5)×0.35=0.5 ,解得 a=0.5?0.330.35+8.5≈8.99
(2)解:(i)每周阅读时间为 [6.5,7.5) 的学生中抽取3名,每周阅读时间为 [7.5,8.5) 的学生中抽取6名.
理由:每周阅读时间为 [6.5,7.5) 与每周阅读时间为 [7.5,8.5) 是差异明显的两层,为保持样本结构与总体结构的一致性,提高样本的代表性,宜采用分层抽样的方法抽取样本;因为两者频率分别为0.1,0.2,所以按照 1:2 进行名额分配.
(ii)由频率分布直方图可知,阅读时间不足8.5小时的学生共有 200×(0.03+0.1+0.2)=66 人,超过8.5小时的共有 200?66=134 人.
于是列联表为:
阅读时间不足8.5小时
阅读时间超过8.5小时
理工类专业
40
60
非理工类专业
26
74
K2 的观测值 k=200×(40×74?26×60)266×134×100×100≈4.432>3.841 ,
所以有 95% 的把握认为学生阅读时间不足与“是否理工类专业”有关
【解析】(1)根据平均数,中位数的定义进行求解即可(2)完成列联表,计算 K2 的观测值,结合独立性检验的性质进行判断即可.
20.【答案】 (1)解:因为 (0.004+0.006+0.02+0.03+0.024+m)×10=1 ,
?解得 m=0.016
所以m的值是 0.016 ;
(2)解:设中位数为a,因为 (0.004+0.006+0.02)×10=0.3
则 (a?70)×0.03=0.2 ,
解得 a=7623 ,
所以抽查学生测试成绩的中位数是 7623 ;
(3)解:抽查的测试平均分为 (0.004×45+0.006×55+0.02×65+0.03×75+0.024×85+0.016×95)×10=76.2 ,
超过75分,
所以该学校通过测试.
【解析】(1)利用已知条件结合频率分布直方图中各小组中小矩形面积等于各小组的频率,再利用频率之和为1,从而求出m的值。
(2)利用已知条件结合频率分布直方图估计出抽查学生测试成绩的中位数。
(3)利用已知条件结合频率分布直方图求出抽查的测试平均分,再利用已知条件抽查的测试平均分超过75分,就表示该学校通过测试,?从而推出该学校通过测试。
满分: 100分 时间: 60分钟
第Ⅰ卷(选择题 共60分)
单项选择题:本题共12小题,每题只有一个选项正确,每小题5分,共计60分。
1.2021年我国推进新冠疫苗全人群免费接种,某小区年龄分布如下图所示,现用分层抽样的方法从该小区所有人中抽取60人进行抗体检测,则从40岁至50岁之间的人群中抽取人数为(??? ).
A.?18??????????????????????????????????????????B.?24??????????????????????????????????????????C.?5??????????????????????????????????????????D.?9
2.某学校组建了演讲,舞蹈?航模?合唱,机器人五个社团,全校 3000 名学生每人都参加且只参加其中一个社团,校团委从这 3000 名学生中随机选取部分学生进行调查,并将调查结果绘制了如下不完整的两个统计图:
则选取的学生中参加机器人社团的学生数为(??? )
A.?50???????????????????????????????????????B.?75???????????????????????????????????????C.?100???????????????????????????????????????D.?125
3.如图,是统计某样本数据得到的频率分布直方图,已知该样本容量为300,则样本数据落在 [6,14) 内的频数为(??? )
A.?68???????????????????????????????????????B.?170???????????????????????????????????????C.?204???????????????????????????????????????D.?240
4.根据食物中维C的含量可大致分为:含量很丰富:鲜枣、沙棘、猕猴桃、柚子,每100克中的维生素C含量超过100毫克;比较丰富:青椒、桂圆、番茄、草莓、甘蓝、黄瓜、柑橘、菜花,每100克中维生素C含量在50~100毫克;相对丰富:白菜、油菜、香菜、菠菜、芹菜、苋菜、菜苔、豌豆、豇豆、萝卜,每100克中维生素C含量在30~50毫克.现从猕猴桃、柚子两种食物中测得每100克所含维生素C的量(单位:mg)得到茎叶图如图所示,则下列说法中不正确的是(??? )
A.?猕猴桃的极差为32
B.?猕猴桃的平均数小于柚子的平均数
C.?猕猴桃的方差小于柚子的方差
D.?柚子的中位数为121
5.为了加强全民爱眼意识,提高民族健康素质,1996年,卫生部,教育部,团中央等12个部委联合发出通知,将爱眼日活动列为国家节日之一,并确定每年的6月6日为“全国爱眼日”.某校高二(1)班有40名学生,学号为01到40,现采用随机数表法从该班抽取5名学生参加“全国爱眼日”宣传活动.已知随机数表中第6行至第7行的各数如下:
16 22 77 94 39?? 49 54 43 54 82?? 17 37 93 23 78?? 87 35 20 96 43? 84 26 34 91 64
84 42 17 53 31?? 57 24 55 06 88?? 77 04 74 47 67?? 21 76 33 50 25? 83 92 12 06 76
若从随机数表第6行第9列的数开始向右读则抽取的第5名学生的学号是(??? )
A.?17?????????????????????????????????????????B.?23?????????????????????????????????????????C.?35?????????????????????????????????????????D.?37
6.某中学初中部有600名学生,高中部有800名学生,其性别比例如图所示,则该校男生比女生多(? ?)
A.?60人??????????????????????????????????B.?100人??????????????????????????????????C.?150人??????????????????????????????????D.?180人
7.某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业者岗位分布条形图,则下列结论中不正确的是(? )
注:90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生.
A.?互联网行业从业人员中90后占一半以上
B.?互联网行业中从事技术岗位的人数超过总人数的20%
C.?互联网行业中从事产品岗位的90后人数超过总人数的5%
D.?互联网行业中从事运营岗位的90后人数比80前人数多
8.某学校为了了解本校学生的上学方式,在全校范围内随机抽查部分学生,了解到上学方式主要有: A ——结伴步行, B ——自行乘车, C ——家人接送, D ——其他方式,并将收集的数据整理绘制成如下两幅不完整的统计图.
根据图中信息,求得本次抽查的学生中 A 类人数是(?? )
A.?30?????????????????????????????????????????B.?40?????????????????????????????????????????C.?42?????????????????????????????????????????D.?48
9.保护生态环境是每个公民应尽的职责!某校随机抽取100名同学进行“垃圾分类”的问卷测试,测试结果发现这100名同学的得分都在 [50,100] 内,按得分分成5组: [50,60) 、 [60,70) 、 [70,80) 、 [80,90) 、 [90,100] ,得到如图所示的频率分布直方图,则估计这100名同学的得分的众数为(??? )
A.?70????????????????????????????????????????B.?72.5????????????????????????????????????????C.?80????????????????????????????????????????D.?75
10.某个小区住户共200户,为调查小区居民的7月份用水量,用分层抽样的方法抽取了50户进行调查,得到本月的用水量(单位:m3)的频率分布直方图如图所示,则小区内用水量超过15 m3的住户的户数为(?? )
A.?10????????????????????????????????????????B.?50????????????????????????????????????????C.?60????????????????????????????????????????D.?140
11.某大学对1000名学生的自主招生水平测试成绩进行统计,得到样本频率分布直方图(如图),则这1000名学生在该次自主招生水平测试中成绩不低于70分的学生数是(???? )
A.?300?????????????????????????????????????B.?400?????????????????????????????????????C.?500?????????????????????????????????????D.?600
12.如图所示的茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩不超过乙的平均成绩的概率为(?? )
A.?45????????????????????????????????????????B.?710????????????????????????????????????????C.?15????????????????????????????????????????D.?910
第Ⅱ卷(非选择题 共40分)
二、填空题:本题共计4小题,共计16分。
13.我国古代数学名著《九章算术》有一抽样问题:“今有北乡若干人,西乡七千四百八十八人,南乡六千九百一十二人,凡三乡,发役三百人,而北乡需遣一百零八人,问北乡人数几何?”其意思为:“今有某地北面若干人,西面有7488人,南面有6912人,这三面要征调300人,而北面征调108人(用分层抽样的方法),则北面共有________人.”
14.为了解学生课外阅读的情况,随机统计了n名学生的课外阅读时间,所得数据都在 [50,150] 中,其频率分布直方图如图所示,已知在 [50,100) 中的频数为 160 ,则n的值为________.
15.某水产养殖场利用100个网箱养殖水产品,收获时测量各箱水产品的产量(单位:kg),其频率分布直方图如图所示,则该养殖场有________个网箱产量不低于50 kg.
16.在某批次的某种灯泡中,随机抽取200个样品.并对其寿命进行追踪调查,将结果列成频率分布表如下:
寿命(天)
频数
频率
[200,300)
40
a
[300,400)
60
0.3
[400,500)
b
0.4
[500,600)
20
0.1
合计
200
1
某人从灯泡样品中随机地购买了 n(n∈N?) 个,如果这 n 个灯泡的寿命情况恰好与按四个组分层抽样所得的结果相同,则 n 的最小值为________.
三、解答题:本题共计4小题,共计24分。
17.为了推进分级诊疗,实现“基层首诊?双向转诊?急慢分治?上下联动”的诊疗模式,某城市自2020年起全面推行家庭医生签约服务.已知该城市居民约为1000万,从0岁到100岁的居民年龄结构的频率分布直方图如图1所示.为了解各年龄段居民签约家庭医生的情况,现调查了1000名年满18周岁的居民,各年龄段被访者签约率如图2所示.
(1)估计该城市年龄在50岁以上且已签约家庭医生的居民人数;
(2)据统计,该城市被访者的签约率约为44%.为把该城市年满18周岁居民的签约率提高到55%以上,应着重提高图2中哪个年龄段的签约率?并根据已有数据陈述理由.
18.为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成A,B两组,每组100只,其中A组小鼠给服甲离子溶液,B组小鼠给服乙离子溶液,每只小鼠给服的溶液体积相同、摩尔浓度相同。经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
记C为事件:“乙离子残留在体内的百分比不低于5.5”,根据直方图得到P(C)的估计值为0.70.
(1)求乙离子残留百分比直方图中a,b的值;
(2)分别估计甲,乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表)
19.? 2019年2月13日《烟台市全民阅读促进条例》全文发布,旨在保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设.某高校为了解条例发布以来全校学生的阅读情况,随机调查了200名学生每周阅读时间 X (单位:小时)并绘制如图所示的频率分布直方图.
(1)求这200名学生每周阅读时间的样本平均数 x 和中位数 a ( a 的值精确到0.01);
(2)为查找影响学生阅读时间的因素,学校团委决定从每周阅读时间为 [6.5,7.5) , [7.5,8.5) 的学生中抽取9名参加座谈会.
(i)你认为9个名额应该怎么分配?并说明理由;
(ii)座谈中发现9名学生中理工类专业的较多.请根据200名学生的调研数据,填写下面的列联表,并判断是否有 95% 的把握认为学生阅读时间不足(每周阅读时间不足8.5小时)与“是否理工类专业”有关?
阅读时间不足8.5小时
阅读时间超过8.5小时
理工类专业
40
60
非理工类专业
附: K2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d) ( n=a+b+c+d ).
临界值表:
P(K2≥k0)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.072
2.706
3.841
5.024
6.635
7.879
10.828
20.2020年5月28日,十三届全国人大三次会议表决通过了《中华人民共和国民法典》,此法典被称为“社会生活的百科全书”,是新中国第一部以法典命名的法律,在法律体系中居于基础性地位,也是市场经济的基本法.民法典与百姓生活密切相关,某学校有800名学生,为了解学生对民法典的认识程度,选取了100名学生进行测试,制成如图所示频率分布直方图.
(1)求m的值;
(2)估计抽查学生测试成绩的中位数;(结果用分数形式表示)
(3)如果抽查的测试平均分超过75分,就表示该学校通过测试,试判断该校能否通过测试.
答案解析
一、单选题
1.【答案】 A
【解析】由条形统计图的数据,根据分层抽样的定义可以知道,
若抽取60人,则从40岁至50岁之间的人群中抽取人数为 60×300200+400+300+100=18 .
故答案为:A.
2.【答案】 B
【解析】由题意,本次调查的人数为 50÷10%=500 人,
其中合唱比赛所占的比例为 200500=0.4=40% ,
所以机器人所占的比例为 1?10%?20%?15%?40%=15%. ,
所以选取的学生中参加机器人社团的学生数为 500×15%=75 人.
故答案为:B.
3.【答案】 C
【解析】样本数据落在 [6,14) 内的频率为 (0.08+0.09)×4=0.68 ,
所以样本数据落在 [6,14) 内的频数为 300×0.68=204 ,
故答案为:C
4.【答案】 C
【解析】解:对于 A ,猕猴桃的极差为: 134?102=32 ,故 A 正确;
对于 B ,猕猴桃的平均数是 x=16(104+102+113+121+122+134)=116 ,
柚子的平均数是 y=16(113+114+121+121+131+132)=122 ,故 B 正确;
对于 C ,猕猴桃的方差是: s12=16(196+144+9+25+36+324)=12213 ,
柚子的方差是: s22=16(81+64+1+1+81+100)=54.67 ,
故猕猴桃的方差大于柚子的方差,故 C 错误;
对于 D ,柚子的中位数是121,故 D 正确;
故答案为:C.
5.【答案】 C
【解析】解:读取的前5名学生的学号依次是:39,17,37,23,35,
故答案为:C.
6.【答案】 B
【解析】解:由题意可得,初中部男生人数为 600×45%=270 ,女生人数为 600?270=330 ;高中部女生人数为 800×40%=320 ,男生人数为 800?320=480 .故该校男生比女生多 480+270?320?330=100 人.
故答案为:B
7.【答案】 C
【解析】A选项,由图可知90后占了56%,故正确;
B选项,互联网行业中90后从事技术岗位中所占比例为 0.56×39.6%=0.22176>0.2 ,互联网行业中从事技术岗位的人数还包括80后,80前,所以互联网行业中从事技术岗位的人数超过总人数的20%,是肯定的,故正确;
C选项,互联网行业中从事产品岗位的90后人数所占比例为 0.56×6.5%=0.0364<0.05 ,故不正确;
D选项,互联网行业中从事运营岗位的90后人数所占比例为 0.56×0.17=0.0952>0.03 ,故正确.
故答案为:C.
8.【答案】 A
【解析】解:根据选择D方式的有18人,所占比例为15%,得总人数为 1815%= 120人,故选择A方式的人数为120﹣42﹣30﹣18=30人.
故答案为:A.
9.【答案】 D
【解析】由频率分布直方图可知,这 100 名同学的得分的众数为 70+802=75 .
故答案为:D.
10.【答案】 C
【解析】从频率分布直方图可知,用水量超过15m?的住户的频率为 (0.05+0.01)×5=0.3 ,即分层抽样的50户中有0.3×50=15户住户的用水量超过15立方米所以小区内用水量超过15立方米的住户户数为 1550×200=60 ,故答案为:C
11.【答案】 D
【解析】该次自主招生水平测试中成绩不低于70分的学生数==?故选D.
12.【答案】 C
【解析】解:由茎叶图知甲的平均成绩为 15 ×(88+89+90+91+92)=90,
∵甲的平均成绩不超过乙的平均成绩,
∴设被污损为x,则乙的平均成绩为 15 ×(83+83+87+99+90+x)≥90,
解得x≥8,
∴甲的平均成绩不超过乙的平均成绩的概率为P= 210=15 .
故答案为:C.
二、填空题
13.【答案】 8100
【解析】因为共抽调300人,北面抽掉了108人,所以西面和南面共14400人中抽出了192人,所以抽样比为 19214400 ,所以北面共有 108×14400192=8100 人,故填8100。
14.【答案】 400
【解析】由频率分布直方图得: [50,100) 的频率为: (0.004+0.012)×25=0.4 ,
∵ 在 [50,100) 中的频数为 160 , ∴n=1600.4=400 .
故答案为: 400 .
15.【答案】 82
【解析】由频率分布直方图,可知不低于50kg的频率为:(0.040+0.070+0.042+0.012)×5=0.82,
所以网箱个数:0.082×100=82.
16.【答案】 10
【解析】由题意得,a=0.2,b=80,由表可知,灯泡样品第一组有40个,第二组有60个,第三组有80个,第四组有20个,所以四个组的比例为2:3:4:1,所以按分层抽样法,购买的灯泡数为n=2k+3k+4k+k =10k( k∈N? ),所以 n 的最小值为10.
三、解答题
17.【答案】 (1)解:该城市年龄在50-60岁的签约人数为: 1000×0.015×10×55.7%=83.55 万;
在60-70岁的签约人数为: 1000×0.010×10×61.7%=61.7 万;
在70-80岁的签约人数为: 1000×0.004×10×70.0%=28 万;
在80岁以上的签约人数为: 1000×0.003×10×75.8%=22.74 万;
故该城市年龄在50岁以上且已签约家庭医生的居民人数为: 83.55+61.7+28+22.74=199.55 万;
(2)解:年龄在10-20岁的人数为: 1000×0.005×10=50 万;
年龄在20-30岁的人数为: 1000×0.018×10=180 万.
所以,年龄在18-30岁的人数大于180万,小于230万,签约率为30.3%;
年龄在30-50岁的人数为 1000×0.037×10=370 万,签约率为37.1%.
年龄在50岁以上的人数为: 1000×0.032×10=320 万,签约率超过55%,上升空间不大.
故由以上数据可知这个城市在30-50岁这个年龄段的人数为370万,基数较其他年龄段是最大的,且签约率非常低,所以为把该地区满18周岁居民的签约率提高到以上,应着重提高30-50这个年龄段的签约率.
【解析】(1)根据题中频率分布直方图与各年龄段被访者的签约率,分别计算50岁以上各年龄段的居民人数,再求和,即可得出结果;
(2)根据题中条件,先确定年龄在18-30岁的人数,年龄在30-50岁的人数,以及年龄在50岁以上的人数,即可确定结果。
18.【答案】 (1)解:由已知得0.70=a+0.20+0.15,故a=0.35.
b=1–0.05–0.15–0.70=0.10.
(2)甲离子残留百分比的平均值的估计值为
2×0.15+3×0.20+4×0.30+5×0.20+6×0.10+7×0.05=4.05.
乙离子残留百分比的平均值的估计值为
3×0.05+4×0.10+5×0.15+6×0.35+7×0.20+8×0.15=6.00.
【解析】(1)由已知利用频率分布直方图,百分比不低于5.5的估计值为0.70列式,即可求出a,b的值;(2)由频率分布直方图平均数的计算公式,利用区间的中点值为代表列式,即可求出平均值.
19.【答案】 (1)解:该组数据的平均数 x=6×0.03+7×0.1+8×0.2+9×0.35+10×0.19 +11×0.09+12×0.04=9 ,
因为 0.03+0.1+0.2+0.35=0.68>0.5 ,所以中位数 a∈[8.5,9.5) ,
由 0.03+0.1+0.2+(a?8.5)×0.35=0.5 ,解得 a=0.5?0.330.35+8.5≈8.99
(2)解:(i)每周阅读时间为 [6.5,7.5) 的学生中抽取3名,每周阅读时间为 [7.5,8.5) 的学生中抽取6名.
理由:每周阅读时间为 [6.5,7.5) 与每周阅读时间为 [7.5,8.5) 是差异明显的两层,为保持样本结构与总体结构的一致性,提高样本的代表性,宜采用分层抽样的方法抽取样本;因为两者频率分别为0.1,0.2,所以按照 1:2 进行名额分配.
(ii)由频率分布直方图可知,阅读时间不足8.5小时的学生共有 200×(0.03+0.1+0.2)=66 人,超过8.5小时的共有 200?66=134 人.
于是列联表为:
阅读时间不足8.5小时
阅读时间超过8.5小时
理工类专业
40
60
非理工类专业
26
74
K2 的观测值 k=200×(40×74?26×60)266×134×100×100≈4.432>3.841 ,
所以有 95% 的把握认为学生阅读时间不足与“是否理工类专业”有关
【解析】(1)根据平均数,中位数的定义进行求解即可(2)完成列联表,计算 K2 的观测值,结合独立性检验的性质进行判断即可.
20.【答案】 (1)解:因为 (0.004+0.006+0.02+0.03+0.024+m)×10=1 ,
?解得 m=0.016
所以m的值是 0.016 ;
(2)解:设中位数为a,因为 (0.004+0.006+0.02)×10=0.3
则 (a?70)×0.03=0.2 ,
解得 a=7623 ,
所以抽查学生测试成绩的中位数是 7623 ;
(3)解:抽查的测试平均分为 (0.004×45+0.006×55+0.02×65+0.03×75+0.024×85+0.016×95)×10=76.2 ,
超过75分,
所以该学校通过测试.
【解析】(1)利用已知条件结合频率分布直方图中各小组中小矩形面积等于各小组的频率,再利用频率之和为1,从而求出m的值。
(2)利用已知条件结合频率分布直方图估计出抽查学生测试成绩的中位数。
(3)利用已知条件结合频率分布直方图求出抽查的测试平均分,再利用已知条件抽查的测试平均分超过75分,就表示该学校通过测试,?从而推出该学校通过测试。
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
