第9章 统计 单元测试A卷-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册(Word含解析)
文档属性
| 名称 | 第9章 统计 单元测试A卷-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册(Word含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 661.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 00:00:00 | ||
图片预览


文档简介
2020—2021学年高一数学下学期第九章单元测试卷
满分: 100分 时间: 60分钟
第Ⅰ卷(选择题 共60分)
单项选择题:本题共12小题,每题只有一个选项正确,每小题5分,共计60分。
1.现要完成下列3项抽样调查:①从10盒饼干中抽取4盒进行食品卫生检查.②报告厅有25排,每排有40个座位,有一次报告会恰好坐满了听众,报告会结束后,为了听取意见,需要请25名听众进行座谈.③某中学共有360名教职工,其中一般教师280名,行政人员55名,后勤人员25名,为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为72的样本.较为合理的抽样方法是( )
A.①简单随机抽样,②系统抽样,③分层抽样
B.①简单随机抽样,②分层抽样,③系统抽样
C.①系统抽样,②简单随机抽样,③分层抽样
D.①分层抽样,②系统抽样,③简单随机抽样
2.下列调查采用的调查方式合适的是( )
A.为了了解炮弹的杀伤力,采用普查的方式
B.为了了解全国中学生的睡眠状况,采用普查的方式
C.为了了解人们保护水资源的意识,采用抽样调查的方式
D.2016年10月17日7时30分,载人飞船“神舟十一号”在酒泉卫星发射中心由长征二号FY11运载火箭成功发射,发射前要对其零部件进行检查,采用抽样调查的方式
3.突如其来的疫情打乱了我们的学习节奏,郑老师为检查网课学习情况,组织了一次网络在线考试,并计算出本次考试中全体学生的平均分为90,方差为65;后来有两位学生反应,自己的成绩被登记错误,一位学生的成绩为88分,记录成78分,另一位学生的成绩为80分,记录成90分,更正后,得到的平均分为false,方差为false,则( )
A.false,false B.false
C.false D.false
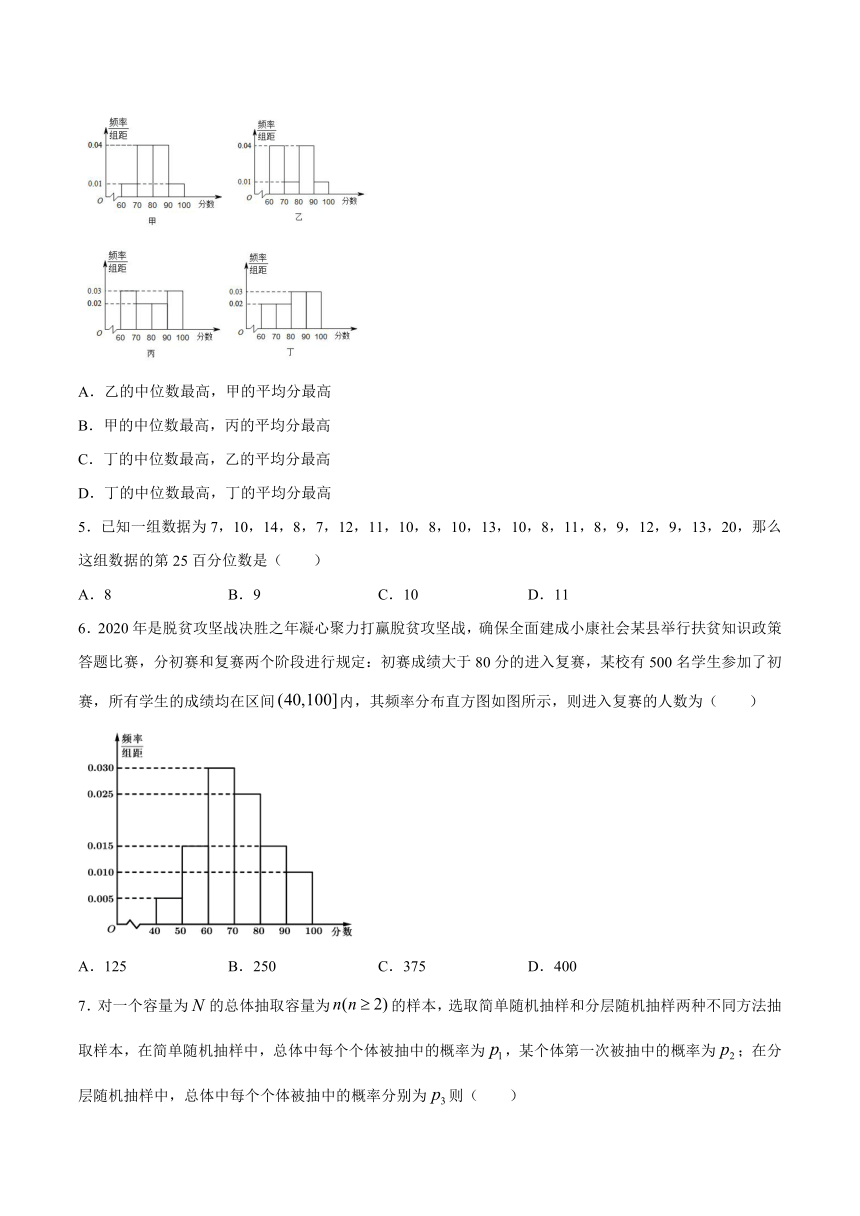
4.甲?乙?丙?丁四位同学在高中学业水平模拟测试中的成绩分布分别为下面的频率分布直方图,估计他们的中位数和平均分(同一组中的数据用该组区间的中点值为代表),正确的是( )
A.乙的中位数最高,甲的平均分最高
B.甲的中位数最高,丙的平均分最高
C.丁的中位数最高,乙的平均分最高
D.丁的中位数最高,丁的平均分最高
5.已知一组数据为7,10,14,8,7,12,11,10,8,10,13,10,8,11,8,9,12,9,13,20,那么这组数据的第25百分位数是( )
A.8 B.9 C.10 D.11
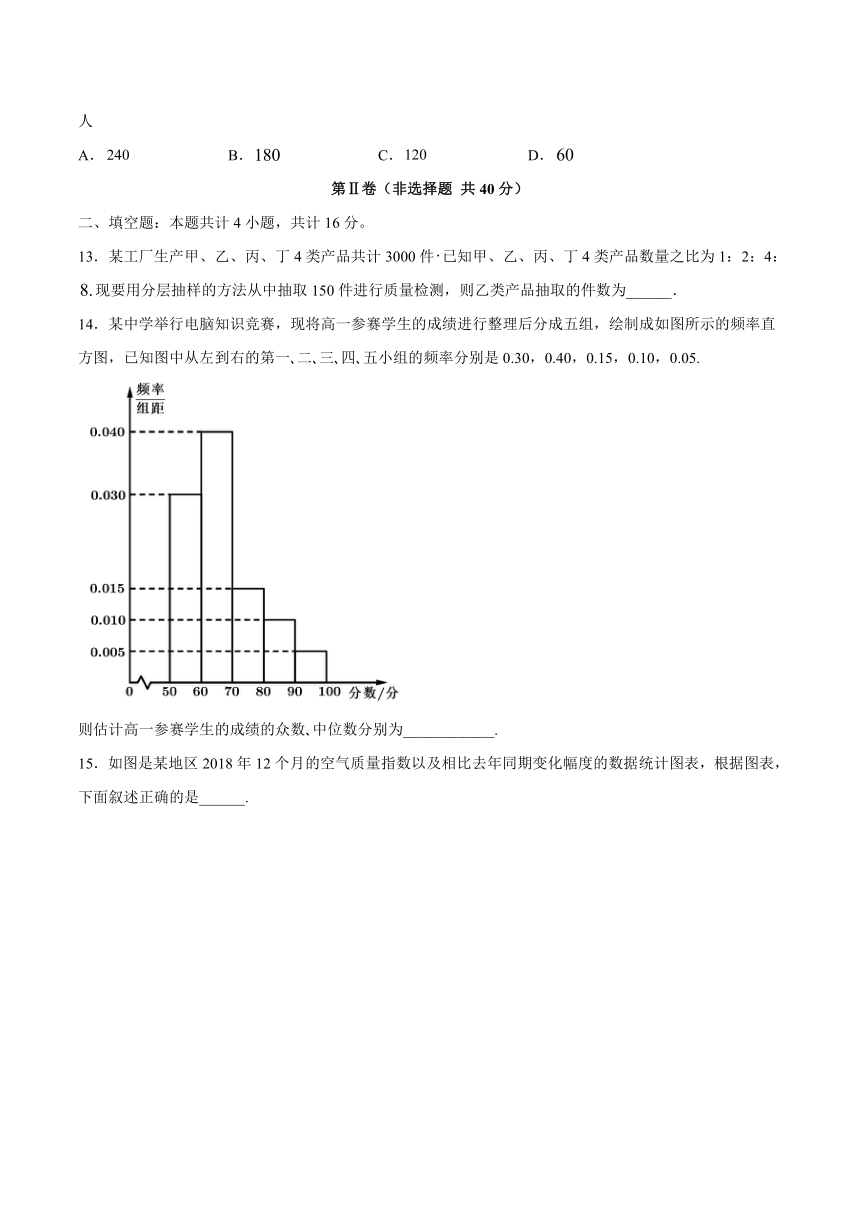
6.2020年是脱贫攻坚战决胜之年凝心聚力打赢脫贫攻坚战,确保全面建成小康社会某县举行扶贫知识政策答题比赛,分初赛和复赛两个阶段进行规定:初赛成绩大于80分的进入复赛,某校有500名学生参加了初赛,所有学生的成绩均在区间false内,其频率分布直方图如图所示,则进入复赛的人数为( )
A.125 B.250 C.375 D.400
7.对一个容量为false的总体抽取容量为false的样本,选取简单随机抽样和分层随机抽样两种不同方法抽取样本,在简单随机抽样中,总体中每个个体被抽中的概率为false,某个体第一次被抽中的概率为false;在分层随机抽样中,总体中每个个体被抽中的概率分别为false则( )
A.false B.false C.false D.false,没有关系
8.甲、乙、丙、丁四名同学在某次军训射击测试中,各射击10次.四人测试成绩对应的条形图如下:
以下关于四名同学射击成绩的数字特征判断不正确的是( )
A.平均数相同 B.中位数相同 C.众数不完全相同 D.丁的方差最大
9.如果false的平均数false,方差false,则false的平均数和方差分别为( )
A.5,5 B.5,4 C.4,3 D.4,2
10.若干年前,某老师刚退休的月退休金为4000元,月退休金各种用途占比统计图如下面的条形图.该老师退休后加强了体育锻炼,目前月退休金的各种用途占比统计图如下面的折线图.已知目前的月就医费比刚退休时少100元,则目前该老师的月退休金为( )
A.5000元 B.5500元 C.6000元 D.6500元
11.样本中共有false个个体,其值分别为false、false、false、false、false.若该样本的平均值为false,则样本的方差为( )
A.false B.false C.false D.false
12.中共一大会址、江西井冈山、贵州遵义、陕西延安是中学生的几个重要的研学旅行地.某中学在校学生false人,学校团委为了了解本校学生到上述红色基地研学旅行的情况,随机调查了false名学生,其中到过中共一大会址或井冈山研学旅行的共有false人,到过井冈山研学旅行的false人,到过中共一大会址并且到过井冈山研学旅行的恰有false人,根据这项调查,估计该学校到过中共一大会址研学旅行的学生大约有( )人
A.false B.false C.false D.false
第Ⅱ卷(非选择题 共40分)
二、填空题:本题共计4小题,共计16分。
13.某工厂生产甲、乙、丙、丁4类产品共计3000件false已知甲、乙、丙、丁4类产品数量之比为1:2:4:false现要用分层抽样的方法从中抽取150件进行质量检测,则乙类产品抽取的件数为______.
14.某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组,绘制成如图所示的频率直方图,已知图中从左到右的第一?二?三?四?五小组的频率分别是0.30,0.40,0.15,0.10,0.05.
则估计高一参赛学生的成绩的众数?中位数分别为____________.
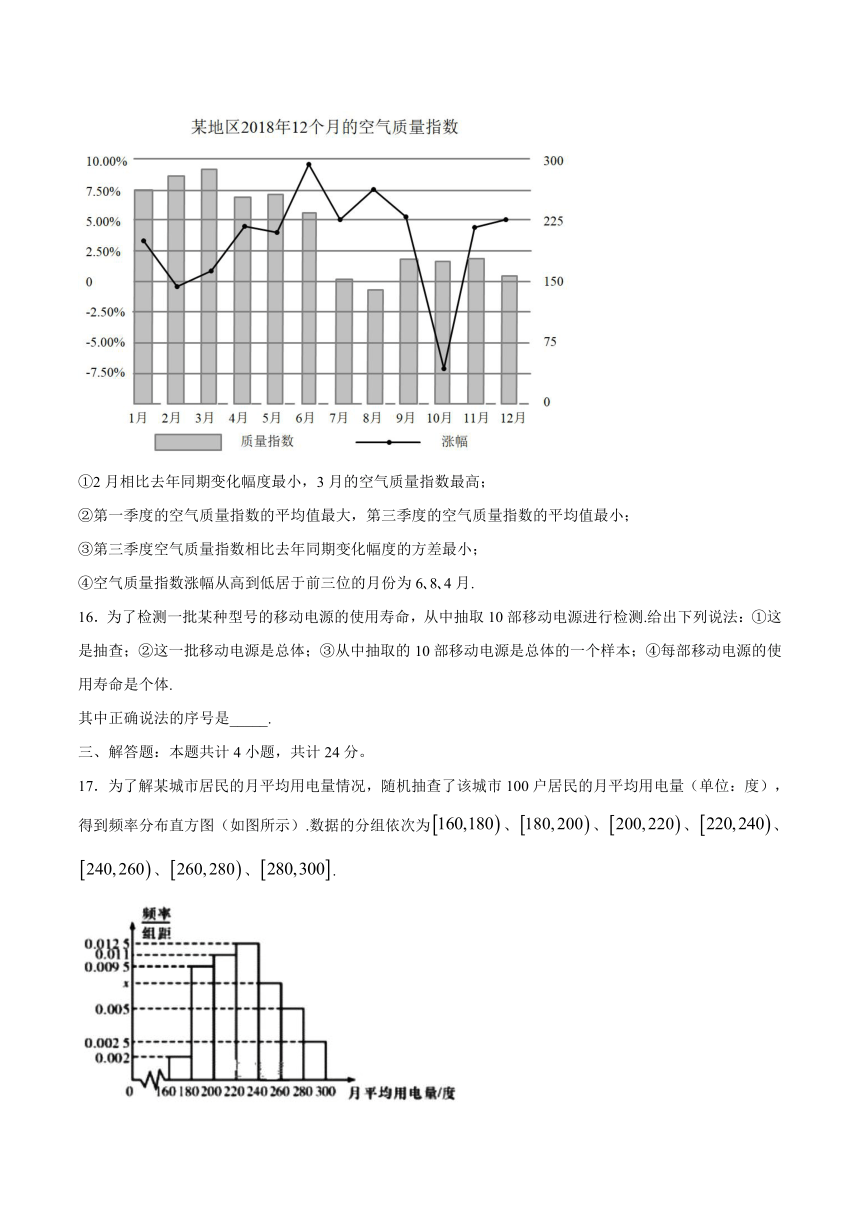
15.如图是某地区2018年12个月的空气质量指数以及相比去年同期变化幅度的数据统计图表,根据图表,下面叙述正确的是______.
①2月相比去年同期变化幅度最小,3月的空气质量指数最高;
②第一季度的空气质量指数的平均值最大,第三季度的空气质量指数的平均值最小;
③第三季度空气质量指数相比去年同期变化幅度的方差最小;
④空气质量指数涨幅从高到低居于前三位的月份为6?8?4月.
16.为了检测一批某种型号的移动电源的使用寿命,从中抽取10部移动电源进行检测.给出下列说法:①这是抽查;②这一批移动电源是总体;③从中抽取的10部移动电源是总体的一个样本;④每部移动电源的使用寿命是个体.
其中正确说法的序号是_____.
三、解答题:本题共计4小题,共计24分。
17.为了解某城市居民的月平均用电量情况,随机抽查了该城市100户居民的月平均用电量(单位:度),得到频率分布直方图(如图所示).数据的分组依次为false、false、false、false、false、false、false.
(1)求频率分布直方图中false的值;
(2)求该城市所有居民月平均用电量的众数和中位数的估计值;
(3)在月平均用电量为false的四组用户中,采用分层抽样的方法抽取false户居民,则应从月用电量在false居民中抽取多少户?
18.某科研课题组通过一款手机APP软件,调查了某市1000名跑步爱好者平均每周的跑步量(简称“周跑量”),得到如下的频数分布表:
周跑量
false
false
false
false
false
false
false
false
false
人数
100
120
130
180
220
150
60
30
10
(1)补全该市1000名跑步爱好者周跑量的频率分布直方图;
周跑量
小于20公
20公里到
不小于40
类别
休闲跑者
核心跑者
精英跑者
装备价格
2500
4000
4500
(2)根据以上图表数据,试求样本的中位数及众数(保留一位小数);
(3)根据跑步爱好者的周跑量,将跑步爱好者分成以下三类,不同类别的跑者购买的装备的价格不一样(如表),根据以上数据,估计该市每位跑步爱好者购买装备,平均需要花费多少元?
19.对某校高二年级学生参加社区服务次数进行统计,随机抽取N名学生作为样本,得到这N名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图:
分组
频数
频率
[3,6)
10
m
[6,9)
n
p
[9,12)
4
q
[12,15)
2
0.05
合计
N
1
(1)求出表中N,p及图中a的值;
(2)请根据题中的频率分布直方图,估计样本的中位数.
20.双十一购物狂欢节,源于淘宝商城(天猫)false年false月false日举办的网络促销活动,目前已成为中国电子商务行业的年度盛事,某商家为了解“双十一”这一天网购者在其网店一次性购物情况,从这一天交易成功的所有订单里随机抽取了false份,按购物金额(单位:元)进行统计,得到如下频率分布直方图(同一组中的数据用该组区间的中点值做代表计算).
(1)求false的值;
(2)试估计购物金额的平均数;
(3)若该商家制订了两种不同的促销方案:
方案一:全场商品打八折;
方案二:全场商品优惠如下表:
购物金额范围
false
false
false
false
false
false
商家优惠(元)
false
false
false
false
false
false
如果你是购物者,你认为哪种方案优惠力度更大?
参考答案
1.A
【详解】
对于①总体中的个体数较少,宜用简单随机抽样;②总体中的个体数较多,而且容易分成均衡的若干部分,选25人刚好25排,每排选一人,宜用系统抽样;③总体是由差异明显的几部分组成,宜用分层抽样.
故选:A.
2.C
【详解】
普查工作量大,有时受客观条件限制,无法对所有个体进行调查,有时调查具有破坏性,不允许普查;
抽样调查范围小,节约时间、人力、物力和财力,但必须注意调查的对象具有代表性和广泛性;
综上可知,只有选项C的调查方式合适.
故选C.
3.B
【详解】
由于false,因此更正前后样本的平均数不发生改变,即false;
由于false,
因此更正后样本的方差变小,即false;
故选:B
4.D
【详解】
甲?乙?丙三位同学的成绩中位数都是80,丁的成绩中位数大于80;
甲的平均成绩为false,
乙的平均成绩为false,
丙的平均成绩为false,
丁的平均成绩为false
故选:D.
5.A
【详解】
解:数据从小到大排列是:
7,7,8,8,8,8,9,9,10,10,10,10,11,11,12,12,13,13,14,20,
共20个数据,false,
所以这组数据的第25百分位数是第5项与第6项数据的平均数,即8,
故选:A.
6.A
【详解】
由直方图可知,成绩大于80分的频率为false,
又∵总人数为500人,所以进入复赛的人数为500×0.25=125,
故选:A.
7.B
【详解】
根据抽样调查的原理可得简单随机抽样,分层抽样都必须满足每个个体被抽到的概率相等,即false.
故选:B.
8.D
【详解】
解:由图的对称性可知,平均数都为false;
由图易知,四组数据的众数不完全相同,中位数相同;
记甲、乙、丙、丁图所对应的方差分别为false,则
false,
false,
false,
false,
所以丙的方差最大.
故选:D.
9.B
【详解】
false的平均数false,
false的平均数为false
false的方差false,
false的方差为false
故选:B
10.A
【详解】
刚退休时就医费用为false元,现在的就医费用为false元,占退休金的false,
因此,目前该教师的月退休金为false元.
故选:A
11.D
【详解】
由题意可知,false,解得false,
因此,该样本的方差为false,故选D.
12.B
【详解】
如下图所示,设调查的学生中去过中共一大会址研学旅行的学生人数为false,
由题意可得false,解的false,
因此,该学校到过中共一大会址研学旅行的学生的人数为false.
故选:B.
13.false
【详解】
解:false甲、乙、丙、丁4类产品共计3000件,已知甲、乙、丙、丁4类产品的数量之比为1:2:4:8,
false用分层抽样的方法从中抽取150件,则乙类产品抽取的件数为false,
故答案为20.
14.65,65
【详解】
由题图可知众数为65,
又∵第一个小矩形的面积为0.3,
∴设中位数为60+x,则0.3+x×0.04=0.5,得x=5,
∴中位数为60+5=65.
故答案为:65,65
15.①②③
【详解】
根据折现统计图可得,2月相比去年同期变化幅度最小,3月的空气质量指数最高,故①正确;
第一季度的空气质量指数的平均值最大,第三季度的空气质量指数的平均值最小,故②正确;
第三季度空气质量指数相比去年同期变化幅度的方差最小,故③正确;
空气质量指数涨幅从高到低居于前三位的月份为6?8?9月,故④错误,
故答案为:①②③.
16.①④
【详解】
根据题意可知,这是抽查,故正确;
总体是这一批移动电源的使用寿命,不是电源本身,故错误;
样本是从中抽取的10部移动电源的使用寿命,不是电源本身,故错误;
每部移动电源的使用寿命是个体,故正确.
故答案为:①④.
17.(1)false;(2)众数为false度,中位数为false度;(3)false户.
【分析】
(1)利用频率分布直方图中所有矩形面积之和为false可求得false的值;
(2)利用频率分布直方图中最高矩形底边的中点值为众数,可得出该城市所有居民月平均用电量的众数,利用中位数左边的矩形面积之和为false可求得该城市所有居民月平均用电量的中位数;
(3)计算出月用电量在false的用户在月平均用电量为false的用户中所占的比例,乘以false可得出结果.
【详解】
(1)因为false,所以false;
(2)月平均用电量众数的估计值为false度,
false,
故中位数false,所以,false,解得false,
故月平均用电量中位数的估计值为false度;
(3)月均用电量在false、false、false、false的用户分别为false户、false户、false户、false户,
其中,月均用电量为false的用户在月平均用电量为false的用户中所占的比例为false,
所以在月均用电量为false的用户中应抽取false(户).
18.(1)见解析;(2)中位数29.2,众数32.5;(3)平均花费3720元.
【分析】
(1)由频数分布表能补全该市1000名跑步爱好者周跑量的频率分布直方图.
(2)由频率分布直方图能求出样本的中位数.
(3)分别求出休闲跑者、核心跑者、精英跑者的人数,由此能估计该市每位跑步爱好者购买装备平均需要花费多少钱.
【详解】
(1)补全该市1000名跑步爱好者周跑量的频率分布直方图,如下:
(2)中位数的估计值:
由false,false,
所以中位数位于区间false中,
设中位数为false,则false,
解得false.即样本中位数是29.2.
因为样本中频率最高的一组为[30,35),所以样本的众数为32.5.
(3)依题意可知,休闲跑者共有false人,
核心跑者false人,
精英跑者false人,
所以该市每位跑步爱好者购买装备,平均需要false元.
即该市每位跑步爱好者购买装备,平均需要3720元.
19.(1)false,false,false;(2)false.
【分析】
(1)根据频率分布表,利用频率false,求出表中N,p,再求出对应矩形的高a的值;
(2)根据中位数左右两边的频率相等,求出中位数的大小.
【详解】
(1)根据频率分布表得,小组false内的频数是false,频率是false,则样本容量是false;
false小组false内的频数是false
对应的频率是false
又组距false,false对应的矩形高为false
(2)设数据的中位数为false,
false小组false内的频率为false,小组false内的频率为false
false数据的中位数在小组false内
false,解得false
样本的中位数为false.
20.(1)false;(2)false元;(3)方案一的优惠力度更大.
【分析】
(1)利用频率分布直方图中所有矩形面积之和为false可计算出false的值;
(2)将每个矩形底边的中点值乘以矩形的面积,相加即可得出购物金额的平均数;
(3)计算出两种方案的优惠金额,从而得出方案一的优惠力度更大.
【详解】
(1)各小组的频率依次为false、false、false、false、false、false.
由false,有false;
(2)购物金额的平均数为false(元);
(3)选择方案一:优惠力度为false元
选择方案二:优惠力度为false(元).
故方案一的优惠力度更大.
满分: 100分 时间: 60分钟
第Ⅰ卷(选择题 共60分)
单项选择题:本题共12小题,每题只有一个选项正确,每小题5分,共计60分。
1.现要完成下列3项抽样调查:①从10盒饼干中抽取4盒进行食品卫生检查.②报告厅有25排,每排有40个座位,有一次报告会恰好坐满了听众,报告会结束后,为了听取意见,需要请25名听众进行座谈.③某中学共有360名教职工,其中一般教师280名,行政人员55名,后勤人员25名,为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为72的样本.较为合理的抽样方法是( )
A.①简单随机抽样,②系统抽样,③分层抽样
B.①简单随机抽样,②分层抽样,③系统抽样
C.①系统抽样,②简单随机抽样,③分层抽样
D.①分层抽样,②系统抽样,③简单随机抽样
2.下列调查采用的调查方式合适的是( )
A.为了了解炮弹的杀伤力,采用普查的方式
B.为了了解全国中学生的睡眠状况,采用普查的方式
C.为了了解人们保护水资源的意识,采用抽样调查的方式
D.2016年10月17日7时30分,载人飞船“神舟十一号”在酒泉卫星发射中心由长征二号FY11运载火箭成功发射,发射前要对其零部件进行检查,采用抽样调查的方式
3.突如其来的疫情打乱了我们的学习节奏,郑老师为检查网课学习情况,组织了一次网络在线考试,并计算出本次考试中全体学生的平均分为90,方差为65;后来有两位学生反应,自己的成绩被登记错误,一位学生的成绩为88分,记录成78分,另一位学生的成绩为80分,记录成90分,更正后,得到的平均分为false,方差为false,则( )
A.false,false B.false
C.false D.false
4.甲?乙?丙?丁四位同学在高中学业水平模拟测试中的成绩分布分别为下面的频率分布直方图,估计他们的中位数和平均分(同一组中的数据用该组区间的中点值为代表),正确的是( )
A.乙的中位数最高,甲的平均分最高
B.甲的中位数最高,丙的平均分最高
C.丁的中位数最高,乙的平均分最高
D.丁的中位数最高,丁的平均分最高
5.已知一组数据为7,10,14,8,7,12,11,10,8,10,13,10,8,11,8,9,12,9,13,20,那么这组数据的第25百分位数是( )
A.8 B.9 C.10 D.11
6.2020年是脱贫攻坚战决胜之年凝心聚力打赢脫贫攻坚战,确保全面建成小康社会某县举行扶贫知识政策答题比赛,分初赛和复赛两个阶段进行规定:初赛成绩大于80分的进入复赛,某校有500名学生参加了初赛,所有学生的成绩均在区间false内,其频率分布直方图如图所示,则进入复赛的人数为( )
A.125 B.250 C.375 D.400
7.对一个容量为false的总体抽取容量为false的样本,选取简单随机抽样和分层随机抽样两种不同方法抽取样本,在简单随机抽样中,总体中每个个体被抽中的概率为false,某个体第一次被抽中的概率为false;在分层随机抽样中,总体中每个个体被抽中的概率分别为false则( )
A.false B.false C.false D.false,没有关系
8.甲、乙、丙、丁四名同学在某次军训射击测试中,各射击10次.四人测试成绩对应的条形图如下:
以下关于四名同学射击成绩的数字特征判断不正确的是( )
A.平均数相同 B.中位数相同 C.众数不完全相同 D.丁的方差最大
9.如果false的平均数false,方差false,则false的平均数和方差分别为( )
A.5,5 B.5,4 C.4,3 D.4,2
10.若干年前,某老师刚退休的月退休金为4000元,月退休金各种用途占比统计图如下面的条形图.该老师退休后加强了体育锻炼,目前月退休金的各种用途占比统计图如下面的折线图.已知目前的月就医费比刚退休时少100元,则目前该老师的月退休金为( )
A.5000元 B.5500元 C.6000元 D.6500元
11.样本中共有false个个体,其值分别为false、false、false、false、false.若该样本的平均值为false,则样本的方差为( )
A.false B.false C.false D.false
12.中共一大会址、江西井冈山、贵州遵义、陕西延安是中学生的几个重要的研学旅行地.某中学在校学生false人,学校团委为了了解本校学生到上述红色基地研学旅行的情况,随机调查了false名学生,其中到过中共一大会址或井冈山研学旅行的共有false人,到过井冈山研学旅行的false人,到过中共一大会址并且到过井冈山研学旅行的恰有false人,根据这项调查,估计该学校到过中共一大会址研学旅行的学生大约有( )人
A.false B.false C.false D.false
第Ⅱ卷(非选择题 共40分)
二、填空题:本题共计4小题,共计16分。
13.某工厂生产甲、乙、丙、丁4类产品共计3000件false已知甲、乙、丙、丁4类产品数量之比为1:2:4:false现要用分层抽样的方法从中抽取150件进行质量检测,则乙类产品抽取的件数为______.
14.某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组,绘制成如图所示的频率直方图,已知图中从左到右的第一?二?三?四?五小组的频率分别是0.30,0.40,0.15,0.10,0.05.
则估计高一参赛学生的成绩的众数?中位数分别为____________.
15.如图是某地区2018年12个月的空气质量指数以及相比去年同期变化幅度的数据统计图表,根据图表,下面叙述正确的是______.
①2月相比去年同期变化幅度最小,3月的空气质量指数最高;
②第一季度的空气质量指数的平均值最大,第三季度的空气质量指数的平均值最小;
③第三季度空气质量指数相比去年同期变化幅度的方差最小;
④空气质量指数涨幅从高到低居于前三位的月份为6?8?4月.
16.为了检测一批某种型号的移动电源的使用寿命,从中抽取10部移动电源进行检测.给出下列说法:①这是抽查;②这一批移动电源是总体;③从中抽取的10部移动电源是总体的一个样本;④每部移动电源的使用寿命是个体.
其中正确说法的序号是_____.
三、解答题:本题共计4小题,共计24分。
17.为了解某城市居民的月平均用电量情况,随机抽查了该城市100户居民的月平均用电量(单位:度),得到频率分布直方图(如图所示).数据的分组依次为false、false、false、false、false、false、false.
(1)求频率分布直方图中false的值;
(2)求该城市所有居民月平均用电量的众数和中位数的估计值;
(3)在月平均用电量为false的四组用户中,采用分层抽样的方法抽取false户居民,则应从月用电量在false居民中抽取多少户?
18.某科研课题组通过一款手机APP软件,调查了某市1000名跑步爱好者平均每周的跑步量(简称“周跑量”),得到如下的频数分布表:
周跑量
false
false
false
false
false
false
false
false
false
人数
100
120
130
180
220
150
60
30
10
(1)补全该市1000名跑步爱好者周跑量的频率分布直方图;
周跑量
小于20公
20公里到
不小于40
类别
休闲跑者
核心跑者
精英跑者
装备价格
2500
4000
4500
(2)根据以上图表数据,试求样本的中位数及众数(保留一位小数);
(3)根据跑步爱好者的周跑量,将跑步爱好者分成以下三类,不同类别的跑者购买的装备的价格不一样(如表),根据以上数据,估计该市每位跑步爱好者购买装备,平均需要花费多少元?
19.对某校高二年级学生参加社区服务次数进行统计,随机抽取N名学生作为样本,得到这N名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图:
分组
频数
频率
[3,6)
10
m
[6,9)
n
p
[9,12)
4
q
[12,15)
2
0.05
合计
N
1
(1)求出表中N,p及图中a的值;
(2)请根据题中的频率分布直方图,估计样本的中位数.
20.双十一购物狂欢节,源于淘宝商城(天猫)false年false月false日举办的网络促销活动,目前已成为中国电子商务行业的年度盛事,某商家为了解“双十一”这一天网购者在其网店一次性购物情况,从这一天交易成功的所有订单里随机抽取了false份,按购物金额(单位:元)进行统计,得到如下频率分布直方图(同一组中的数据用该组区间的中点值做代表计算).
(1)求false的值;
(2)试估计购物金额的平均数;
(3)若该商家制订了两种不同的促销方案:
方案一:全场商品打八折;
方案二:全场商品优惠如下表:
购物金额范围
false
false
false
false
false
false
商家优惠(元)
false
false
false
false
false
false
如果你是购物者,你认为哪种方案优惠力度更大?
参考答案
1.A
【详解】
对于①总体中的个体数较少,宜用简单随机抽样;②总体中的个体数较多,而且容易分成均衡的若干部分,选25人刚好25排,每排选一人,宜用系统抽样;③总体是由差异明显的几部分组成,宜用分层抽样.
故选:A.
2.C
【详解】
普查工作量大,有时受客观条件限制,无法对所有个体进行调查,有时调查具有破坏性,不允许普查;
抽样调查范围小,节约时间、人力、物力和财力,但必须注意调查的对象具有代表性和广泛性;
综上可知,只有选项C的调查方式合适.
故选C.
3.B
【详解】
由于false,因此更正前后样本的平均数不发生改变,即false;
由于false,
因此更正后样本的方差变小,即false;
故选:B
4.D
【详解】
甲?乙?丙三位同学的成绩中位数都是80,丁的成绩中位数大于80;
甲的平均成绩为false,
乙的平均成绩为false,
丙的平均成绩为false,
丁的平均成绩为false
故选:D.
5.A
【详解】
解:数据从小到大排列是:
7,7,8,8,8,8,9,9,10,10,10,10,11,11,12,12,13,13,14,20,
共20个数据,false,
所以这组数据的第25百分位数是第5项与第6项数据的平均数,即8,
故选:A.
6.A
【详解】
由直方图可知,成绩大于80分的频率为false,
又∵总人数为500人,所以进入复赛的人数为500×0.25=125,
故选:A.
7.B
【详解】
根据抽样调查的原理可得简单随机抽样,分层抽样都必须满足每个个体被抽到的概率相等,即false.
故选:B.
8.D
【详解】
解:由图的对称性可知,平均数都为false;
由图易知,四组数据的众数不完全相同,中位数相同;
记甲、乙、丙、丁图所对应的方差分别为false,则
false,
false,
false,
false,
所以丙的方差最大.
故选:D.
9.B
【详解】
false的平均数false,
false的平均数为false
false的方差false,
false的方差为false
故选:B
10.A
【详解】
刚退休时就医费用为false元,现在的就医费用为false元,占退休金的false,
因此,目前该教师的月退休金为false元.
故选:A
11.D
【详解】
由题意可知,false,解得false,
因此,该样本的方差为false,故选D.
12.B
【详解】
如下图所示,设调查的学生中去过中共一大会址研学旅行的学生人数为false,
由题意可得false,解的false,
因此,该学校到过中共一大会址研学旅行的学生的人数为false.
故选:B.
13.false
【详解】
解:false甲、乙、丙、丁4类产品共计3000件,已知甲、乙、丙、丁4类产品的数量之比为1:2:4:8,
false用分层抽样的方法从中抽取150件,则乙类产品抽取的件数为false,
故答案为20.
14.65,65
【详解】
由题图可知众数为65,
又∵第一个小矩形的面积为0.3,
∴设中位数为60+x,则0.3+x×0.04=0.5,得x=5,
∴中位数为60+5=65.
故答案为:65,65
15.①②③
【详解】
根据折现统计图可得,2月相比去年同期变化幅度最小,3月的空气质量指数最高,故①正确;
第一季度的空气质量指数的平均值最大,第三季度的空气质量指数的平均值最小,故②正确;
第三季度空气质量指数相比去年同期变化幅度的方差最小,故③正确;
空气质量指数涨幅从高到低居于前三位的月份为6?8?9月,故④错误,
故答案为:①②③.
16.①④
【详解】
根据题意可知,这是抽查,故正确;
总体是这一批移动电源的使用寿命,不是电源本身,故错误;
样本是从中抽取的10部移动电源的使用寿命,不是电源本身,故错误;
每部移动电源的使用寿命是个体,故正确.
故答案为:①④.
17.(1)false;(2)众数为false度,中位数为false度;(3)false户.
【分析】
(1)利用频率分布直方图中所有矩形面积之和为false可求得false的值;
(2)利用频率分布直方图中最高矩形底边的中点值为众数,可得出该城市所有居民月平均用电量的众数,利用中位数左边的矩形面积之和为false可求得该城市所有居民月平均用电量的中位数;
(3)计算出月用电量在false的用户在月平均用电量为false的用户中所占的比例,乘以false可得出结果.
【详解】
(1)因为false,所以false;
(2)月平均用电量众数的估计值为false度,
false,
故中位数false,所以,false,解得false,
故月平均用电量中位数的估计值为false度;
(3)月均用电量在false、false、false、false的用户分别为false户、false户、false户、false户,
其中,月均用电量为false的用户在月平均用电量为false的用户中所占的比例为false,
所以在月均用电量为false的用户中应抽取false(户).
18.(1)见解析;(2)中位数29.2,众数32.5;(3)平均花费3720元.
【分析】
(1)由频数分布表能补全该市1000名跑步爱好者周跑量的频率分布直方图.
(2)由频率分布直方图能求出样本的中位数.
(3)分别求出休闲跑者、核心跑者、精英跑者的人数,由此能估计该市每位跑步爱好者购买装备平均需要花费多少钱.
【详解】
(1)补全该市1000名跑步爱好者周跑量的频率分布直方图,如下:
(2)中位数的估计值:
由false,false,
所以中位数位于区间false中,
设中位数为false,则false,
解得false.即样本中位数是29.2.
因为样本中频率最高的一组为[30,35),所以样本的众数为32.5.
(3)依题意可知,休闲跑者共有false人,
核心跑者false人,
精英跑者false人,
所以该市每位跑步爱好者购买装备,平均需要false元.
即该市每位跑步爱好者购买装备,平均需要3720元.
19.(1)false,false,false;(2)false.
【分析】
(1)根据频率分布表,利用频率false,求出表中N,p,再求出对应矩形的高a的值;
(2)根据中位数左右两边的频率相等,求出中位数的大小.
【详解】
(1)根据频率分布表得,小组false内的频数是false,频率是false,则样本容量是false;
false小组false内的频数是false
对应的频率是false
又组距false,false对应的矩形高为false
(2)设数据的中位数为false,
false小组false内的频率为false,小组false内的频率为false
false数据的中位数在小组false内
false,解得false
样本的中位数为false.
20.(1)false;(2)false元;(3)方案一的优惠力度更大.
【分析】
(1)利用频率分布直方图中所有矩形面积之和为false可计算出false的值;
(2)将每个矩形底边的中点值乘以矩形的面积,相加即可得出购物金额的平均数;
(3)计算出两种方案的优惠金额,从而得出方案一的优惠力度更大.
【详解】
(1)各小组的频率依次为false、false、false、false、false、false.
由false,有false;
(2)购物金额的平均数为false(元);
(3)选择方案一:优惠力度为false元
选择方案二:优惠力度为false(元).
故方案一的优惠力度更大.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
