第10章 概率 单元测试B卷-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册(Word含解析)
文档属性
| 名称 | 第10章 概率 单元测试B卷-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册(Word含解析) | 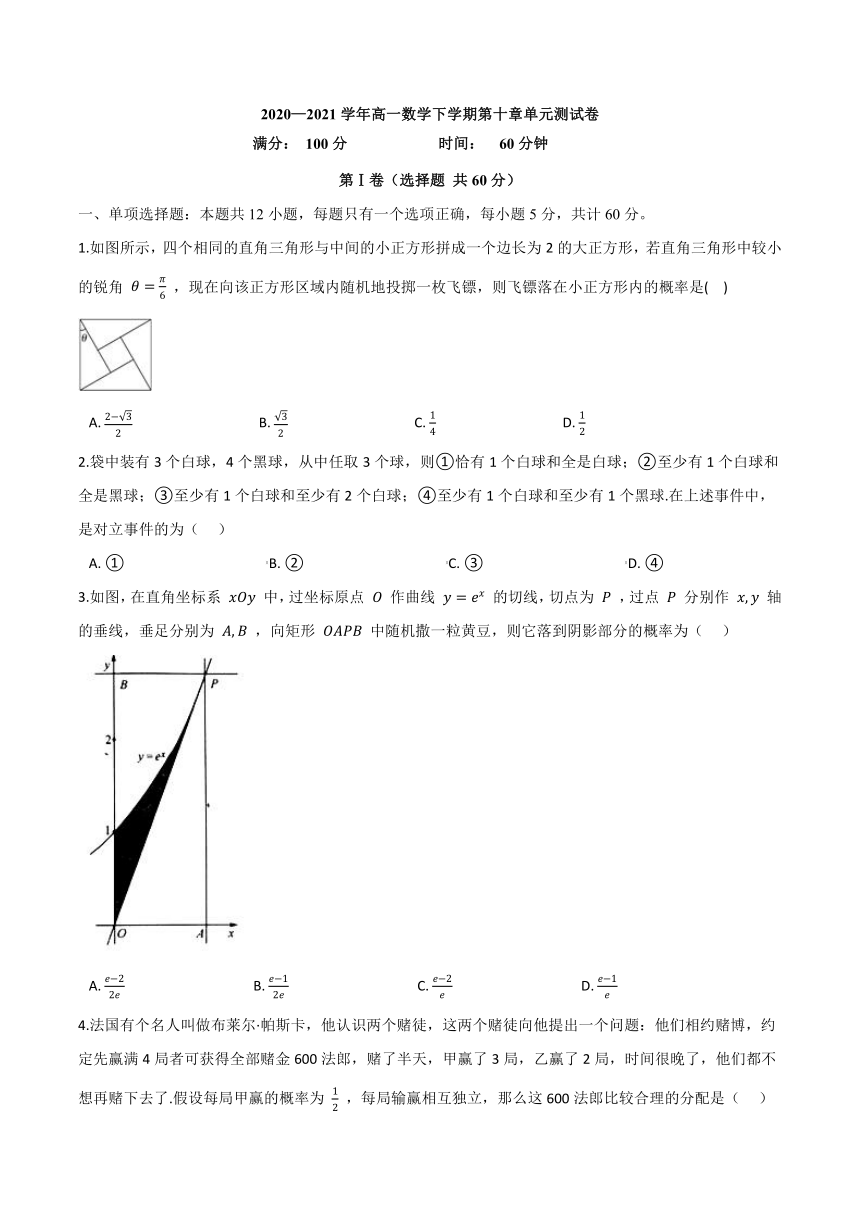 | |
| 格式 | docx | ||
| 文件大小 | 158.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 17:11:07 | ||
图片预览




文档简介
2020—2021学年高一数学下学期第十章单元测试卷
满分: 100分 时间: 60分钟
第Ⅰ卷(选择题 共60分)
单项选择题:本题共12小题,每题只有一个选项正确,每小题5分,共计60分。
1.如图所示,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角 θ=π6 ,现在向该正方形区域内随机地投掷一枚飞镖,则飞镖落在小正方形内的概率是(?? )
A.?2?32?????????????????????????????????????B.?32?????????????????????????????????????C.?14?????????????????????????????????????D.?12
2.袋中装有3个白球,4个黑球,从中任取3个球,则①恰有1个白球和全是白球;②至少有1个白球和全是黑球;③至少有1个白球和至少有2个白球;④至少有1个白球和至少有1个黑球.在上述事件中,是对立事件的为(??? )
A.?①?????????????????????????????????????????B.?②?????????????????????????????????????????C.?③?????????????????????????????????????????D.?④
3.如图,在直角坐标系 xOy 中,过坐标原点 O 作曲线 y=ex 的切线,切点为 P ,过点 P 分别作 x,y 轴的垂线,垂足分别为 A,B ,向矩形 OAPB 中随机撒一粒黄豆,则它落到阴影部分的概率为(??? )
A.?e?22e?????????????????????????????????????B.?e?12e?????????????????????????????????????C.?e?2e?????????????????????????????????????D.?e?1e
4.法国有个名人叫做布莱尔·帕斯卡,他认识两个赌徒,这两个赌徒向他提出一个问题:他们相约赌博,约定先赢满4局者可获得全部赌金600法郎,赌了半天,甲赢了3局,乙赢了2局,时间很晚了,他们都不想再赌下去了.假设每局甲赢的概率为 12 ,每局输赢相互独立,那么这600法郎比较合理的分配是(??? )
A.?甲300法郎,乙300法郎
B.?甲480法郎,乙120法郎
C.?甲450法郎,乙150法郎
D.?甲400法郎,乙200法郎
5.一张储蓄卡的密码共有6位数字,每位数字都可以从 0?9 中任选一个,某人在银行自动提款机上取钱时,忘记了密码最后一位数字,如果任意按最后一位数字,不超过2次就按对的概率为(?? )
A.?25????????????????????????????????????????B.?310????????????????????????????????????????C.?15????????????????????????????????????????D.?110
6.已知某运动员每次投篮命中的概率低于40%,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为(?? )
A.?0.35?????????????????????????????????????B.?0.25?????????????????????????????????????C.?0.20?????????????????????????????????????D.?0.15
7.某高二学生练习篮球,每次投篮命中率约30%,现采用随机模拟的方法估计该生投篮命中的概率;先用计算器产生0到9之间的整数值的随机数,指定0,1,2表示命中,4,5,6,7,8,9表示不命中;再以每三个随机数为一组,代表3次投篮的结果.经随机模拟产生了如下随机数:
807 956 191 925 271 932 813 458 569 683
431 257 393 027 556 488 730 113 527 989
据此估计该生3次投篮恰有2次命中的概率约为( )
A.?0.15?????????????????????????????????????B.?0.25?????????????????????????????????????C.?0.2?????????????????????????????????????D.?0.18
8.口袋里放有大小相同的两个红球和一个白球,有放回地每次摸一个球,定义数列 {an} : an={?1?????第n次摸取红球1???????第n次摸取白球 ,如果 Sn 是数列 {an} 的前 n 项和,那么 S7=3 的概率是(?? )
A.?C75·(13)2÷(23)5????????????????B.?C72·(23)2?(13)5????????????????C.?C75·(13)2?(13)5????????????????D.?C73·(13)2?(23)5
9.某社区为了更好的开展便民服务,对一周内居民办理业务所需要的时间进行统计,结果如下表.假设居民办理业务所需要的时间相互独立,且都是整数分钟.
办理业务所需要的时间(分)
1
2
3
4
5
频率
0.1
0.3
0.4
0.1
0.1
则在某一天,第三位居民恰好等待4分钟才开始办理业务的概率为(??? )
A.?0.04?????????????????????????????????????B.?0.08?????????????????????????????????????C.?0.17?????????????????????????????????????D.?0.26
10.世界著名的数学杂志《美国数学月刊》于1989年曾刊登过一个红极一时的棋盘问题.题中的正六边形棋盘,用三种全等(仅朝向和颜色不同)的菱形图案全部填满(如下图),若在棋盘内随机取一点,则此点取自白色区域的概率为(??? )
A.?16?????????????????????????????????????????B.?13?????????????????????????????????????????C.?14?????????????????????????????????????????D.?516
11.从装有两个红球和三个黑球的口袋里任取两个球,那么互斥而不对立的两个事件是( ??)
A.?“至少有一个黑球”与“都是黑球”??????????????????B.?“至少有一个黑球”与“至少有一个红球”
C.?“恰好有一个黑球”与“恰好有两个黑球”????????D.?“至少有一个黑球”与“都是红球”
12.设M,N为两个随机事件,给出以下命题:
(1.)若M、N为互斥事件,且 P(M)=15 , P(N)=14 ,则 P(M∪N)=920 ;
(2.)若 P(M)=12 , P(N)=13 , P(MN)=16 ,则M、N为相互独立事件;
(3.)若 P(M)=12 , P(N)=13 , P(MN)=16 ,则M、N为相互独立事件;
(4.)若 P(M)=12 , P(N)=13 , P(MN)=16 ,则M、N为相互独立事件;
(5.)若 P(M)=12 , P(N)=13 , P(MN)=56 ,则M、N为相互独立事件;
其中正确命题的个数为(?? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
第Ⅱ卷(非选择题 共40分)
二、填空题:本题共计4小题,共计16分。
13.已知甲?乙?丙三位选手参加的某次投掷飞镖的比赛,比赛规则如下:①每场比赛有两位选手参加,并决出胜负;②每场比赛获胜的选手与未参加此场比赛的选手进行下一场的比赛;③在比赛中,若有一个选手首先获胜两场,则本次比赛结束,该选手就获得此次飞镖比赛第一名.若在每场比赛中,均没有平局,且甲胜乙的概率为 12 ,甲胜丙的概率为 23 ,乙胜丙的概率为 13 ,且甲与乙先赛,则甲获得第一名的概率为________.
14.“全国部分大学附中教学协作体”成立于1991年,由湖南师大附中,福建师大附中,陕西师大附中,南开大学附中,辽宁师大附中和云南师大附中在长沙发起年会倡议,九十年代末期首都师大附中和山东师大附中相继加盟.今年10月协作体第二十九届年会在我校举行,在年会联谊会的舞台左右两端分别挂有两串彩灯,这两串彩灯的第一次闪亮是相互独立的,且都在通电后4秒内的任一时刻等可能的闪亮.那么在两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过2秒的概率为________.
15.如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分,在正方形ABCD中任取一点P,则点P恰好取自阴影部分的概率为________.
16.甲乙两辆车去同一货场装货物,货场每次只能给一辆车装货物,所以若两辆车同时到达,则需要有一辆车等待.已知甲、乙两车装货物需要的时间都为20分钟,倘若甲、乙两车都在某1小时内到达该货场(在此期间货场没有其他车辆),则至少有一辆车需要等待装货物的概率是________.
三、解答题:本题共计4小题,共计24分。
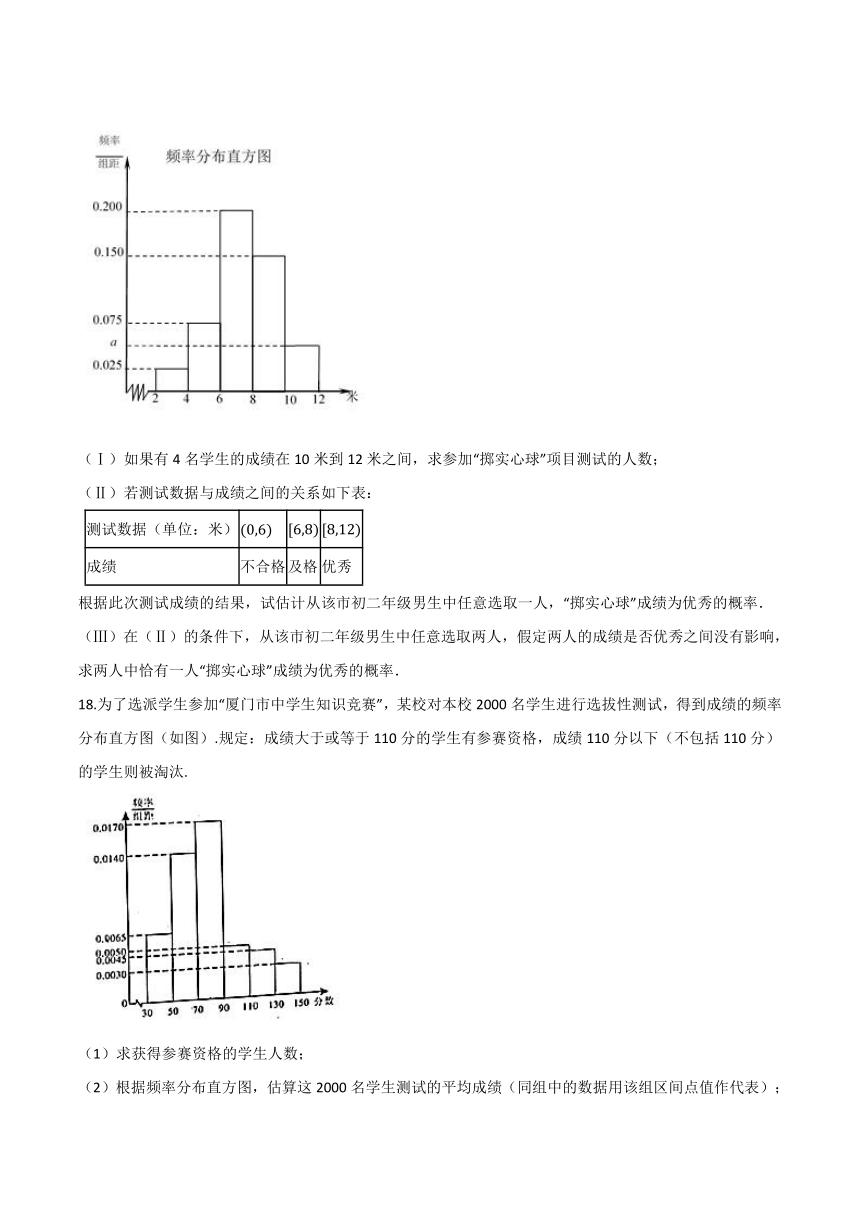
17.为了解某市今年初二年级男生的身体素质状况,从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试.经统计,成绩均在2米到12米之间,把获得的所有数据平均分成 [2,4),[4,6),[6,8),[8,10),[10,12] 五组,得到频率分布直方图如图所示.
(Ⅰ)如果有4名学生的成绩在10米到12米之间,求参加“掷实心球”项目测试的人数;
(Ⅱ)若测试数据与成绩之间的关系如下表:
测试数据(单位:米)
(0,6)
[6,8)
[8,12)
成绩
不合格
及格
优秀
根据此次测试成绩的结果,试估计从该市初二年级男生中任意选取一人,“掷实心球”成绩为优秀的概率.
(Ⅲ)在(Ⅱ)的条件下,从该市初二年级男生中任意选取两人,假定两人的成绩是否优秀之间没有影响,求两人中恰有一人“掷实心球”成绩为优秀的概率.
18.为了选派学生参加“厦门市中学生知识竞赛”,某校对本校2000名学生进行选拔性测试,得到成绩的频率分布直方图(如图).规定:成绩大于或等于110分的学生有参赛资格,成绩110分以下(不包括110分)的学生则被淘汰.
(1)求获得参赛资格的学生人数;
(2)根据频率分布直方图,估算这2000名学生测试的平均成绩(同组中的数据用该组区间点值作代表);
(3)若知识竞赛分初赛和复赛,在初赛中有两种答题方案:
方案一:每人从5道备选题中任意抽出1道,若答对,则可参加复赛,否则被淘汰;
方案二:每人从5道备选题中任意抽出3道,若至少答对其中2道,则可参加复赛,否则被海汰.
已知学生甲只会5道备选题中的3道,那么甲选择哪种答题方案,进入复赛的可能性更大?并说明理由.
19.射手张强在一次射击中射中10环、9环、8环、7环、7环以下的概率分别是0.24、0.28、0.19、0.16、0.13.计算这个射手在一次射击中:
(1)射中10环或9环的概率;
(2)至少射中7环的概率;
(3)射中环数小于8环的概率.
20.某中学从参加高一年级上学期期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)估计这次考试的及格率(60分及以上为及格).
(2)从成绩是70分以上(包括70分)的学生中选一人,求选到第一名学生的概率(第一名学生只一人).
答案解析
一、单选题
1.【答案】 A
【解析】观察这个图可知:大正方形的边长为2,总面积为4,
而小正方形区域的边长为 3?1 ,面积为 4?23 ,
故飞镖落在小正方形区域的概率 4?234=2?32 ,
故答案为:A。
2.【答案】 B
【解析】有3个白球,4个黑球,从中任取3个球:①是互斥事件,但不是对立事件;②是互斥事件,同时也是对立事件;③既不是互斥事件,也不是对立事件;④既不是互斥事件,也不是对立事件;
故答案为:B
3.【答案】 A
【解析】设切点 P(x0,ex0) , y′=ex
所以切线方程 y?ex0=ex0(x?x0) ,又因为过原点
所以 0?ex0=ex0(0?x0) 解得 x0=1 ?
所以点P (1,e) ?
因为 y=ex 与 x 轴在 [0,1] 围成的面积是 01exdx=e?1 ?
则阴影部分的面积为 e?1?e2=e2?1 ?
而矩形 OAPB 的面积为 e ?
故向矩形 OAPB 中随机撒一粒黄豆,则它落到阴影部分的概率为 e2?1e=e?22e ?
故答案为:A
4.【答案】 C
【解析】解:根据题意,在甲赢了3局,乙赢了2局后,
甲获得全部赌金600法郎的概率 P1=12+12×12=34 ,
乙获得全部赌金600法郎的概率 P2=12×12=14 ,
则这600法郎应该分配给甲 600×34=450 法郎,分配给乙 600×14=150 法郎,
故答案为:C.
5.【答案】 C
【解析】一张储蓄卡的密码共有6位数字,每位数字都可以从0~9中任选一个,
某人在银行自动提款机上取钱时,忘记了密码最后一位数字,
任意按最后一位数字,不超过2次就按对的概率为:
p= 110+910×19 = 15 .
故答案为:C.
6.【答案】 B
【解析】解:由题意知模拟三次投篮的结果,经随机模拟产生了如下20组随机数,
在20组随机数中表示三次投篮恰有两次命中的有:191、271、932、812、393.
共5组随机数,
∴所求概率为 520=14 =0.25.
故选B.
7.【答案】 C
【解析】解:由已知可得:
产生的随机数共有20组,
其中表示3次投篮恰有2次的有:
191,271,027,113,共4组,
所以估计概率为 .
故选C.
8.【答案】 B
【解析】解:由题意 S7=3 说明共摸球七次,只有两次摸到红球,
由于每次摸球的结果数之间没有影响,摸到红球的概率是 23 ,
摸到白球的概率是 13 ,
故只有两次摸到红球的概率是 C72?(23)2?(13)5 .
故答案为:B.
9.【答案】 C
【解析】因为第三位居民恰好等待4分钟才开始办理业务,
若前两位居民办理业务分别用两分钟,则对应概率为 0.3×0.3=0.09 ;
若前两位居民办理业务的时间分别为:1分钟和三分钟,则对应的概率为 0.1×0.4+0.4×0.1=0.08 ;
因此,第三位居民恰好等待4分钟才开始办理业务的概率为 0.09+0.08=0.17 .
故答案为:C.
10.【答案】 B
【解析】直接数出正六边形共包含菱形48个,其中白色16个,
则此点此点取自白色区域的概率 =白色区域面积正六边形面积=1648=13 .
故答案为:B.
11.【答案】 C
【解析】解:从装有两个红球和三个黑球的口袋里任取两个球,
在A中,“至少有一个黑球”与“都是黑球”能同时发生,不是互斥事件,A不符合题意;
在B中,“至少有一个黑球”与“至少有一个红球”能同时发生,不是互斥事件,B不符合题意;
在C中,“恰好有一个黑球”与“恰好有两个黑球”不能同时发生,
但能同时不发生,是互斥而不对立的两个事件,C符合题意;
在D中,“至少有一个黑球”与“都是红球”是对立事件,D不符合题意.
故答案为:C
12.【答案】 D
【解析】解:在(1)中,若M、N为互斥事件,且 P(M)=15 , P(N)=14 ,
则P(M∪N)= 15+14 = 920 ,故(1)正确;
在(2)中,若 P(M)=12 , P(N)=13 , P(MN)=16 ,
则由相互独立事件乘法公式知M、N为相互独立事件,故(2)正确;
在(3)中,若 P(M)=12 , P(N)=13 , P(MN)=16 ,
则由对立事件概率计算公式和相互独立事件乘法公式知M、N为相互独立事件,故(3)正确;
在(4)中,若 P(M)=12 , P(N)=13 , P(MN)=16 ,
当M、N为相互独立事件时,P(MN)= 12×23=13 ,故(4)错误;
(5.)若 P(M)=12 , P(N)=13 , P(MN)=56 ,
则由对立事件概率计算公式和相互独立事件乘法公式知M、N为相互独立事件,故(5)正确.
故选:D.
二、填空题
13.【答案】 1736
【解析】因为每场比赛中,甲胜乙的概率为 12 ,甲胜丙的概率为 23 ,乙胜丙的概率为 13 ,则甲选手获胜有以下三种情况:1.甲胜乙?甲胜丙;2甲胜乙?丙胜甲?乙胜丙?甲胜乙;3乙胜甲?丙胜乙?甲胜丙?甲胜乙;
所以甲选手获胜的概率是 P(A)=12×23+12×(1?23)×13×12+(1?12)×(1?13)×23×12=1736 .
故答案为: 1736
14.【答案】 34
【解析】设第一串彩灯闪亮的时刻为 x 秒,
第二串彩灯闪亮的时刻为 y 秒,
基本事件的总区域 Ω={(x,y)|0≤x≤4,0≤y≤4} ,
满足闪亮时刻相差不超过2秒的事件
A={(x,y)||x?y|≤2,0≤x≤4,0≤y≤4} ,
作出事件 A 表示的区域(阴影部分).
P(A)=1?2×12×2×216=34
故答案为: 34
15.【答案】23
【解析】解:由题意,建立如图所示的坐标系,则D(2,1), 设抛物线方程为y2=2px,代入D,可得p= 14 ,∴y= 12x ,
∴S= 20212xdx = 2?23x32|02 = 83 ,
∴点P恰好取自阴影部分的概率为 834 = 23 ,
故答案为: 23 .
16.【答案】59
【解析】解:设现在时间是0,甲乙到场的时间分别是x y, 那么就会有:
0≤x≤60,
0≤y≤60,
|x﹣y|如果小于20,就是等待事件,
否则不用等待了.画出来坐标轴如下图
两条斜直线见的面积是等待,
外面的两个三角形面积是不等待,
∴至少有一辆车需要等待装货物的概率:
p= 60×60?2×12×40×4060×60 = 59 .
三、解答题
17.【答案】 解:(Ⅰ)由题意可知 (0.2+0.15+0.075+a+0.025)×2=1 ,解得 a=0.05 .
所以此次测试总人数为 40.05×2=40 .
故此次参加“掷实心球”的项目测试的人数为40人
(Ⅱ)设“从该市初二年级男生中任意选取一人,“掷实心球”成绩为优秀”为事件 A .
由图可知,参加此次“掷实心球”的项目测试的初二男生,
成绩优秀的频率为 (0.15+0.05)×2=0.4 ,
则估计 P(A)=0.4 .
(Ⅲ)记事件 Ai :第 i 名男生成绩优秀,其中 i=1,2 .两人中恰有一人成绩优秀可以表示为 A1A2+A2A1 ,
因为 A1,A2 相互独立, A2,A1 相互独立,
所以 P(A1A2)=P(A1)P(A2)=0.24 , P(A2A1)=P(A2)P(A1)=0.24 ,
又因为 A1A2,A2A1 互斥,
所以 P(A1A2+A2A1)=P(A1A2)+P(A2A1)=0.48 .
所以两人中恰有一人“掷实心球”成绩为优秀的概率为 0.48 .
【解析】(Ⅰ)由频率分布直方图能求出a.再有4名学生的成绩在10米到12米之间,求出成绩在10米到12米之间的频率,由此能示出参加“掷实心球”项目测试的人数(Ⅱ)求出频率分布直方图得成绩在8米至12米(含8米和12米)的频率,由此估计从该市初二年级男生中任意选取一人,“掷实心球”成绩为优秀的概率(Ⅲ)记事件 Ai :第 i 名男生成绩优秀,其中 i=1,2 .两人中恰有一人成绩优秀可以表示为 A1A2+A2A1 ,根据相互独立事件同时发生的概率及互斥事件和的概率公式求解即可.
18.【答案】 (1)解:成绩大于或等于110分的学生频率为 (0.0045+0.0030)×20=0.15
所以获得参赛资格的学生人数为 0.15×2000=300 ;
(2)解:平均成绩为 0.0065×20×40+0.0140×20×60+0.0170×20×80+0.0050×20×100
+0.0045×20×120+0.0030×20×140=78.4
(3)解:方案一:甲进入复赛的概率为 35 ;
方案二:甲进入复赛的概率为 C33+C32C21C53=710>35
所以甲选方案二答题方案,进入复赛的可能性更大.
【解析】(1)计算成绩大于或等于110分的学生频率,再求频数即得结果;(2)根据组中值计算平均数;(3)分别计算两个方案进入复赛的概率,比较大小确定最终方案.
19.【答案】 (1)解:设“射中10环”、“射中9环”、“射中8环”、“射中7环”、“射中7环以下”的事件分别为A,B,C,D,E,
则射中10环或9环的概率P(A∪B)=P(A)+P(B)=0.24+0.28=0.52.
所以,射中10环或9环的概率为0.52
(2)解:至少射中7环的概率P(A∪B∪C∪D)=P(A)+P(B)+P(C)+P(D)=0.24+0.28+0.19+0.16=0.87.
所以,至少射中7环的概率为0.87
(3)解:射中环数小于8环的概率P(D∪E)=P(D)+P(E)=0.16+0.13=0.29.
所以,射中环数小于8环的概率为0.29
【解析】(1)设“射中10环”、“射中9环”、“射中8环”、“射中7环”、“射中7环以下”的事件分别为A,B,C,D,E,则射中10环或9环的概率为P(A∪B)=P(A)+P(B),由此能求出结果.(2)至少射中7环的概率P(A∪B∪C∪D)=P(A)+P(B)+P(C)+P(D),由此能求出结果.(3)射中环数小于8环的概率P(D∪E)=P(D)+P(E),由此能求出结果.
20.【答案】 (1)解:依题意,60及以上的分数所在的第三、四、五、六组,
频率和为 (0.015+0.03+0.025+0.005)?10=0.75 ,
所以,抽样学生成绩的合格率是 75 %.
(2)解: "[70,?80) , [80,?90) , [90,?100] ”的人数是18,15,3.
所以从成绩是70分以上(包括70分)的学生中选一人,
选到第一名的概率 P=136.
【解析】(1)根据频率分布直方图的意义,小矩形的面积即为相应概率。
(2)[70,100]的人数共有36人,由概率的意义知 P = 136。
满分: 100分 时间: 60分钟
第Ⅰ卷(选择题 共60分)
单项选择题:本题共12小题,每题只有一个选项正确,每小题5分,共计60分。
1.如图所示,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角 θ=π6 ,现在向该正方形区域内随机地投掷一枚飞镖,则飞镖落在小正方形内的概率是(?? )
A.?2?32?????????????????????????????????????B.?32?????????????????????????????????????C.?14?????????????????????????????????????D.?12
2.袋中装有3个白球,4个黑球,从中任取3个球,则①恰有1个白球和全是白球;②至少有1个白球和全是黑球;③至少有1个白球和至少有2个白球;④至少有1个白球和至少有1个黑球.在上述事件中,是对立事件的为(??? )
A.?①?????????????????????????????????????????B.?②?????????????????????????????????????????C.?③?????????????????????????????????????????D.?④
3.如图,在直角坐标系 xOy 中,过坐标原点 O 作曲线 y=ex 的切线,切点为 P ,过点 P 分别作 x,y 轴的垂线,垂足分别为 A,B ,向矩形 OAPB 中随机撒一粒黄豆,则它落到阴影部分的概率为(??? )
A.?e?22e?????????????????????????????????????B.?e?12e?????????????????????????????????????C.?e?2e?????????????????????????????????????D.?e?1e
4.法国有个名人叫做布莱尔·帕斯卡,他认识两个赌徒,这两个赌徒向他提出一个问题:他们相约赌博,约定先赢满4局者可获得全部赌金600法郎,赌了半天,甲赢了3局,乙赢了2局,时间很晚了,他们都不想再赌下去了.假设每局甲赢的概率为 12 ,每局输赢相互独立,那么这600法郎比较合理的分配是(??? )
A.?甲300法郎,乙300法郎
B.?甲480法郎,乙120法郎
C.?甲450法郎,乙150法郎
D.?甲400法郎,乙200法郎
5.一张储蓄卡的密码共有6位数字,每位数字都可以从 0?9 中任选一个,某人在银行自动提款机上取钱时,忘记了密码最后一位数字,如果任意按最后一位数字,不超过2次就按对的概率为(?? )
A.?25????????????????????????????????????????B.?310????????????????????????????????????????C.?15????????????????????????????????????????D.?110
6.已知某运动员每次投篮命中的概率低于40%,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为(?? )
A.?0.35?????????????????????????????????????B.?0.25?????????????????????????????????????C.?0.20?????????????????????????????????????D.?0.15
7.某高二学生练习篮球,每次投篮命中率约30%,现采用随机模拟的方法估计该生投篮命中的概率;先用计算器产生0到9之间的整数值的随机数,指定0,1,2表示命中,4,5,6,7,8,9表示不命中;再以每三个随机数为一组,代表3次投篮的结果.经随机模拟产生了如下随机数:
807 956 191 925 271 932 813 458 569 683
431 257 393 027 556 488 730 113 527 989
据此估计该生3次投篮恰有2次命中的概率约为( )
A.?0.15?????????????????????????????????????B.?0.25?????????????????????????????????????C.?0.2?????????????????????????????????????D.?0.18
8.口袋里放有大小相同的两个红球和一个白球,有放回地每次摸一个球,定义数列 {an} : an={?1?????第n次摸取红球1???????第n次摸取白球 ,如果 Sn 是数列 {an} 的前 n 项和,那么 S7=3 的概率是(?? )
A.?C75·(13)2÷(23)5????????????????B.?C72·(23)2?(13)5????????????????C.?C75·(13)2?(13)5????????????????D.?C73·(13)2?(23)5
9.某社区为了更好的开展便民服务,对一周内居民办理业务所需要的时间进行统计,结果如下表.假设居民办理业务所需要的时间相互独立,且都是整数分钟.
办理业务所需要的时间(分)
1
2
3
4
5
频率
0.1
0.3
0.4
0.1
0.1
则在某一天,第三位居民恰好等待4分钟才开始办理业务的概率为(??? )
A.?0.04?????????????????????????????????????B.?0.08?????????????????????????????????????C.?0.17?????????????????????????????????????D.?0.26
10.世界著名的数学杂志《美国数学月刊》于1989年曾刊登过一个红极一时的棋盘问题.题中的正六边形棋盘,用三种全等(仅朝向和颜色不同)的菱形图案全部填满(如下图),若在棋盘内随机取一点,则此点取自白色区域的概率为(??? )
A.?16?????????????????????????????????????????B.?13?????????????????????????????????????????C.?14?????????????????????????????????????????D.?516
11.从装有两个红球和三个黑球的口袋里任取两个球,那么互斥而不对立的两个事件是( ??)
A.?“至少有一个黑球”与“都是黑球”??????????????????B.?“至少有一个黑球”与“至少有一个红球”
C.?“恰好有一个黑球”与“恰好有两个黑球”????????D.?“至少有一个黑球”与“都是红球”
12.设M,N为两个随机事件,给出以下命题:
(1.)若M、N为互斥事件,且 P(M)=15 , P(N)=14 ,则 P(M∪N)=920 ;
(2.)若 P(M)=12 , P(N)=13 , P(MN)=16 ,则M、N为相互独立事件;
(3.)若 P(M)=12 , P(N)=13 , P(MN)=16 ,则M、N为相互独立事件;
(4.)若 P(M)=12 , P(N)=13 , P(MN)=16 ,则M、N为相互独立事件;
(5.)若 P(M)=12 , P(N)=13 , P(MN)=56 ,则M、N为相互独立事件;
其中正确命题的个数为(?? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
第Ⅱ卷(非选择题 共40分)
二、填空题:本题共计4小题,共计16分。
13.已知甲?乙?丙三位选手参加的某次投掷飞镖的比赛,比赛规则如下:①每场比赛有两位选手参加,并决出胜负;②每场比赛获胜的选手与未参加此场比赛的选手进行下一场的比赛;③在比赛中,若有一个选手首先获胜两场,则本次比赛结束,该选手就获得此次飞镖比赛第一名.若在每场比赛中,均没有平局,且甲胜乙的概率为 12 ,甲胜丙的概率为 23 ,乙胜丙的概率为 13 ,且甲与乙先赛,则甲获得第一名的概率为________.
14.“全国部分大学附中教学协作体”成立于1991年,由湖南师大附中,福建师大附中,陕西师大附中,南开大学附中,辽宁师大附中和云南师大附中在长沙发起年会倡议,九十年代末期首都师大附中和山东师大附中相继加盟.今年10月协作体第二十九届年会在我校举行,在年会联谊会的舞台左右两端分别挂有两串彩灯,这两串彩灯的第一次闪亮是相互独立的,且都在通电后4秒内的任一时刻等可能的闪亮.那么在两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过2秒的概率为________.
15.如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分,在正方形ABCD中任取一点P,则点P恰好取自阴影部分的概率为________.
16.甲乙两辆车去同一货场装货物,货场每次只能给一辆车装货物,所以若两辆车同时到达,则需要有一辆车等待.已知甲、乙两车装货物需要的时间都为20分钟,倘若甲、乙两车都在某1小时内到达该货场(在此期间货场没有其他车辆),则至少有一辆车需要等待装货物的概率是________.
三、解答题:本题共计4小题,共计24分。
17.为了解某市今年初二年级男生的身体素质状况,从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试.经统计,成绩均在2米到12米之间,把获得的所有数据平均分成 [2,4),[4,6),[6,8),[8,10),[10,12] 五组,得到频率分布直方图如图所示.
(Ⅰ)如果有4名学生的成绩在10米到12米之间,求参加“掷实心球”项目测试的人数;
(Ⅱ)若测试数据与成绩之间的关系如下表:
测试数据(单位:米)
(0,6)
[6,8)
[8,12)
成绩
不合格
及格
优秀
根据此次测试成绩的结果,试估计从该市初二年级男生中任意选取一人,“掷实心球”成绩为优秀的概率.
(Ⅲ)在(Ⅱ)的条件下,从该市初二年级男生中任意选取两人,假定两人的成绩是否优秀之间没有影响,求两人中恰有一人“掷实心球”成绩为优秀的概率.
18.为了选派学生参加“厦门市中学生知识竞赛”,某校对本校2000名学生进行选拔性测试,得到成绩的频率分布直方图(如图).规定:成绩大于或等于110分的学生有参赛资格,成绩110分以下(不包括110分)的学生则被淘汰.
(1)求获得参赛资格的学生人数;
(2)根据频率分布直方图,估算这2000名学生测试的平均成绩(同组中的数据用该组区间点值作代表);
(3)若知识竞赛分初赛和复赛,在初赛中有两种答题方案:
方案一:每人从5道备选题中任意抽出1道,若答对,则可参加复赛,否则被淘汰;
方案二:每人从5道备选题中任意抽出3道,若至少答对其中2道,则可参加复赛,否则被海汰.
已知学生甲只会5道备选题中的3道,那么甲选择哪种答题方案,进入复赛的可能性更大?并说明理由.
19.射手张强在一次射击中射中10环、9环、8环、7环、7环以下的概率分别是0.24、0.28、0.19、0.16、0.13.计算这个射手在一次射击中:
(1)射中10环或9环的概率;
(2)至少射中7环的概率;
(3)射中环数小于8环的概率.
20.某中学从参加高一年级上学期期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)估计这次考试的及格率(60分及以上为及格).
(2)从成绩是70分以上(包括70分)的学生中选一人,求选到第一名学生的概率(第一名学生只一人).
答案解析
一、单选题
1.【答案】 A
【解析】观察这个图可知:大正方形的边长为2,总面积为4,
而小正方形区域的边长为 3?1 ,面积为 4?23 ,
故飞镖落在小正方形区域的概率 4?234=2?32 ,
故答案为:A。
2.【答案】 B
【解析】有3个白球,4个黑球,从中任取3个球:①是互斥事件,但不是对立事件;②是互斥事件,同时也是对立事件;③既不是互斥事件,也不是对立事件;④既不是互斥事件,也不是对立事件;
故答案为:B
3.【答案】 A
【解析】设切点 P(x0,ex0) , y′=ex
所以切线方程 y?ex0=ex0(x?x0) ,又因为过原点
所以 0?ex0=ex0(0?x0) 解得 x0=1 ?
所以点P (1,e) ?
因为 y=ex 与 x 轴在 [0,1] 围成的面积是 01exdx=e?1 ?
则阴影部分的面积为 e?1?e2=e2?1 ?
而矩形 OAPB 的面积为 e ?
故向矩形 OAPB 中随机撒一粒黄豆,则它落到阴影部分的概率为 e2?1e=e?22e ?
故答案为:A
4.【答案】 C
【解析】解:根据题意,在甲赢了3局,乙赢了2局后,
甲获得全部赌金600法郎的概率 P1=12+12×12=34 ,
乙获得全部赌金600法郎的概率 P2=12×12=14 ,
则这600法郎应该分配给甲 600×34=450 法郎,分配给乙 600×14=150 法郎,
故答案为:C.
5.【答案】 C
【解析】一张储蓄卡的密码共有6位数字,每位数字都可以从0~9中任选一个,
某人在银行自动提款机上取钱时,忘记了密码最后一位数字,
任意按最后一位数字,不超过2次就按对的概率为:
p= 110+910×19 = 15 .
故答案为:C.
6.【答案】 B
【解析】解:由题意知模拟三次投篮的结果,经随机模拟产生了如下20组随机数,
在20组随机数中表示三次投篮恰有两次命中的有:191、271、932、812、393.
共5组随机数,
∴所求概率为 520=14 =0.25.
故选B.
7.【答案】 C
【解析】解:由已知可得:
产生的随机数共有20组,
其中表示3次投篮恰有2次的有:
191,271,027,113,共4组,
所以估计概率为 .
故选C.
8.【答案】 B
【解析】解:由题意 S7=3 说明共摸球七次,只有两次摸到红球,
由于每次摸球的结果数之间没有影响,摸到红球的概率是 23 ,
摸到白球的概率是 13 ,
故只有两次摸到红球的概率是 C72?(23)2?(13)5 .
故答案为:B.
9.【答案】 C
【解析】因为第三位居民恰好等待4分钟才开始办理业务,
若前两位居民办理业务分别用两分钟,则对应概率为 0.3×0.3=0.09 ;
若前两位居民办理业务的时间分别为:1分钟和三分钟,则对应的概率为 0.1×0.4+0.4×0.1=0.08 ;
因此,第三位居民恰好等待4分钟才开始办理业务的概率为 0.09+0.08=0.17 .
故答案为:C.
10.【答案】 B
【解析】直接数出正六边形共包含菱形48个,其中白色16个,
则此点此点取自白色区域的概率 =白色区域面积正六边形面积=1648=13 .
故答案为:B.
11.【答案】 C
【解析】解:从装有两个红球和三个黑球的口袋里任取两个球,
在A中,“至少有一个黑球”与“都是黑球”能同时发生,不是互斥事件,A不符合题意;
在B中,“至少有一个黑球”与“至少有一个红球”能同时发生,不是互斥事件,B不符合题意;
在C中,“恰好有一个黑球”与“恰好有两个黑球”不能同时发生,
但能同时不发生,是互斥而不对立的两个事件,C符合题意;
在D中,“至少有一个黑球”与“都是红球”是对立事件,D不符合题意.
故答案为:C
12.【答案】 D
【解析】解:在(1)中,若M、N为互斥事件,且 P(M)=15 , P(N)=14 ,
则P(M∪N)= 15+14 = 920 ,故(1)正确;
在(2)中,若 P(M)=12 , P(N)=13 , P(MN)=16 ,
则由相互独立事件乘法公式知M、N为相互独立事件,故(2)正确;
在(3)中,若 P(M)=12 , P(N)=13 , P(MN)=16 ,
则由对立事件概率计算公式和相互独立事件乘法公式知M、N为相互独立事件,故(3)正确;
在(4)中,若 P(M)=12 , P(N)=13 , P(MN)=16 ,
当M、N为相互独立事件时,P(MN)= 12×23=13 ,故(4)错误;
(5.)若 P(M)=12 , P(N)=13 , P(MN)=56 ,
则由对立事件概率计算公式和相互独立事件乘法公式知M、N为相互独立事件,故(5)正确.
故选:D.
二、填空题
13.【答案】 1736
【解析】因为每场比赛中,甲胜乙的概率为 12 ,甲胜丙的概率为 23 ,乙胜丙的概率为 13 ,则甲选手获胜有以下三种情况:1.甲胜乙?甲胜丙;2甲胜乙?丙胜甲?乙胜丙?甲胜乙;3乙胜甲?丙胜乙?甲胜丙?甲胜乙;
所以甲选手获胜的概率是 P(A)=12×23+12×(1?23)×13×12+(1?12)×(1?13)×23×12=1736 .
故答案为: 1736
14.【答案】 34
【解析】设第一串彩灯闪亮的时刻为 x 秒,
第二串彩灯闪亮的时刻为 y 秒,
基本事件的总区域 Ω={(x,y)|0≤x≤4,0≤y≤4} ,
满足闪亮时刻相差不超过2秒的事件
A={(x,y)||x?y|≤2,0≤x≤4,0≤y≤4} ,
作出事件 A 表示的区域(阴影部分).
P(A)=1?2×12×2×216=34
故答案为: 34
15.【答案】23
【解析】解:由题意,建立如图所示的坐标系,则D(2,1), 设抛物线方程为y2=2px,代入D,可得p= 14 ,∴y= 12x ,
∴S= 20212xdx = 2?23x32|02 = 83 ,
∴点P恰好取自阴影部分的概率为 834 = 23 ,
故答案为: 23 .
16.【答案】59
【解析】解:设现在时间是0,甲乙到场的时间分别是x y, 那么就会有:
0≤x≤60,
0≤y≤60,
|x﹣y|如果小于20,就是等待事件,
否则不用等待了.画出来坐标轴如下图
两条斜直线见的面积是等待,
外面的两个三角形面积是不等待,
∴至少有一辆车需要等待装货物的概率:
p= 60×60?2×12×40×4060×60 = 59 .
三、解答题
17.【答案】 解:(Ⅰ)由题意可知 (0.2+0.15+0.075+a+0.025)×2=1 ,解得 a=0.05 .
所以此次测试总人数为 40.05×2=40 .
故此次参加“掷实心球”的项目测试的人数为40人
(Ⅱ)设“从该市初二年级男生中任意选取一人,“掷实心球”成绩为优秀”为事件 A .
由图可知,参加此次“掷实心球”的项目测试的初二男生,
成绩优秀的频率为 (0.15+0.05)×2=0.4 ,
则估计 P(A)=0.4 .
(Ⅲ)记事件 Ai :第 i 名男生成绩优秀,其中 i=1,2 .两人中恰有一人成绩优秀可以表示为 A1A2+A2A1 ,
因为 A1,A2 相互独立, A2,A1 相互独立,
所以 P(A1A2)=P(A1)P(A2)=0.24 , P(A2A1)=P(A2)P(A1)=0.24 ,
又因为 A1A2,A2A1 互斥,
所以 P(A1A2+A2A1)=P(A1A2)+P(A2A1)=0.48 .
所以两人中恰有一人“掷实心球”成绩为优秀的概率为 0.48 .
【解析】(Ⅰ)由频率分布直方图能求出a.再有4名学生的成绩在10米到12米之间,求出成绩在10米到12米之间的频率,由此能示出参加“掷实心球”项目测试的人数(Ⅱ)求出频率分布直方图得成绩在8米至12米(含8米和12米)的频率,由此估计从该市初二年级男生中任意选取一人,“掷实心球”成绩为优秀的概率(Ⅲ)记事件 Ai :第 i 名男生成绩优秀,其中 i=1,2 .两人中恰有一人成绩优秀可以表示为 A1A2+A2A1 ,根据相互独立事件同时发生的概率及互斥事件和的概率公式求解即可.
18.【答案】 (1)解:成绩大于或等于110分的学生频率为 (0.0045+0.0030)×20=0.15
所以获得参赛资格的学生人数为 0.15×2000=300 ;
(2)解:平均成绩为 0.0065×20×40+0.0140×20×60+0.0170×20×80+0.0050×20×100
+0.0045×20×120+0.0030×20×140=78.4
(3)解:方案一:甲进入复赛的概率为 35 ;
方案二:甲进入复赛的概率为 C33+C32C21C53=710>35
所以甲选方案二答题方案,进入复赛的可能性更大.
【解析】(1)计算成绩大于或等于110分的学生频率,再求频数即得结果;(2)根据组中值计算平均数;(3)分别计算两个方案进入复赛的概率,比较大小确定最终方案.
19.【答案】 (1)解:设“射中10环”、“射中9环”、“射中8环”、“射中7环”、“射中7环以下”的事件分别为A,B,C,D,E,
则射中10环或9环的概率P(A∪B)=P(A)+P(B)=0.24+0.28=0.52.
所以,射中10环或9环的概率为0.52
(2)解:至少射中7环的概率P(A∪B∪C∪D)=P(A)+P(B)+P(C)+P(D)=0.24+0.28+0.19+0.16=0.87.
所以,至少射中7环的概率为0.87
(3)解:射中环数小于8环的概率P(D∪E)=P(D)+P(E)=0.16+0.13=0.29.
所以,射中环数小于8环的概率为0.29
【解析】(1)设“射中10环”、“射中9环”、“射中8环”、“射中7环”、“射中7环以下”的事件分别为A,B,C,D,E,则射中10环或9环的概率为P(A∪B)=P(A)+P(B),由此能求出结果.(2)至少射中7环的概率P(A∪B∪C∪D)=P(A)+P(B)+P(C)+P(D),由此能求出结果.(3)射中环数小于8环的概率P(D∪E)=P(D)+P(E),由此能求出结果.
20.【答案】 (1)解:依题意,60及以上的分数所在的第三、四、五、六组,
频率和为 (0.015+0.03+0.025+0.005)?10=0.75 ,
所以,抽样学生成绩的合格率是 75 %.
(2)解: "[70,?80) , [80,?90) , [90,?100] ”的人数是18,15,3.
所以从成绩是70分以上(包括70分)的学生中选一人,
选到第一名的概率 P=136.
【解析】(1)根据频率分布直方图的意义,小矩形的面积即为相应概率。
(2)[70,100]的人数共有36人,由概率的意义知 P = 136。
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
