第10章 概率 单元测试A卷-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册(Word含解析)
文档属性
| 名称 | 第10章 概率 单元测试A卷-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册(Word含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 881.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 17:11:27 | ||
图片预览




文档简介
2020—2021学年高一数学下学期第十章单元测试卷
满分: 100分 时间: 60分钟
第Ⅰ卷(选择题 共60分)
单项选择题:本题共12小题,每题只有一个选项正确,每小题5分,共计60分。
1.吸烟有害健康,小明为了帮助爸爸戒烟,在爸爸包里放一个小盒子,里面随机摆放三支香烟和三支跟香烟外形完全一样的“戒烟口香糖”,并且和爸爸约定,每次想吸烟时,从盒子里任取一支,若取到口香糖则吃一支口香糖,不吸烟;若取到香烟,则吸一支烟,不吃口香糖,假设每次香烟和口香糖被取到的可能性相同,则“口香糖吃完时还剩2支香烟”的概率为( )
A.false B.false
C.false D.false
2.一个电路如图所示,A,B,C,D,E,F为6个开关,其闭合的概率为false,且是相互独立的,则灯亮的概率是( )
A.false B.false C.false D.false
3.将编号分别为1,2,3,4,5的5个小球分别放入3个不同的盒子中,每个盒子都不空,则每个盒子中所放小球的编号奇偶性均不相同的概率为
A.false B.false C.false D.false
4.我国古代有着辉煌的数学研究成果,其中《周髀算经》、《九章算术》、《海岛算经》、《数书九章》、《缉古算经》、《缀术》有丰富多彩的内容,是了解我国古代数学的重要文献,这6部专著中有4部产生于汉、魏、晋、南北朝时期.某中学拟从这6部专著中选择2部作为“数学文化”校本课程学习内容,则所选2部专著中恰有1部是汉、魏、晋、南北朝时期专著的概率为( )
A.false B.false C.false D.false
5.将一枚质地均匀的硬币向上抛掷10次,其中“正面朝上恰好有5次”是( )
A.必然事件 B.随机事件
C.不可能事件 D.无法确定
6.甲抛掷均匀硬币2017次,乙抛掷均匀硬币2016次,下列四个随机事件的概率是0.5的是( )
①甲抛出正面次数比乙抛出正面次数多;
②甲抛出反面次数比乙抛出正面次数少;
③甲抛出反面次数比甲抛出正面次数多;
④乙抛出正面次数与乙抛出反面次数一样多.
A.①② B.①③ C.②③ D.②④
7.从一批产品中取出三件产品,设事件A为“三件产品全不是次品”,事件B为“三件产品全是次品”,事件C为“三件产品至少有一件是次品”,则下列结论正确的是( )
A.B与C互斥 B.任何两个均互斥
C.A与C互斥 D.任何两个均不互斥
8.在北京消费季活动中,某商场为促销举行购物抽奖活动,规定购物消费每满200元就可以参加一次抽奖活动,中奖的概率为false.那么以下理解正确的是( )
A.某顾客抽奖10次,一定能中奖1次
B.某顾客抽奖10次,可能1次也没中奖
C.某顾客消费210元,一定不能中奖
D.某顾客消费1000元,至少能中奖1次
9.在一个袋子中放false个白球,false个红球,摇匀后随机摸出false个球,与“摸出false个白球false个红球”互斥而不对立的事件是( )
A.至少摸出false个白球 B.至少摸出false个红球
C.摸出false个白球 D.摸出false个白球或摸出false个红球
10.对空中飞行的飞机连续射击两次,每次发射一枚炮弹,设A=“两次都击中飞机”,B=“两次都没击中飞机”,C=“恰有一枚炮弹击中飞机”,D=“至少有一枚炮弹击中飞机”,下列关系不正确的是( )
A.A?D B.B∩D=false
C.A∪C=D D.A∪B=B∪D
11.若某群体中的成员只用现金支付的概率为0.4,既用现金支付也用非现金支付的概率为0.3,则不用现金支付的概率为( )
A.0.4 B.0.3 C.0.7 D.0.6
12.从一批产品中取出三件产品,设A=“至多一件次品”, B=“至少一件次品”,C=“三件产品全是次品”,D=“恰有一件次品”,则下列结论正确的是( )
A.A与B是互斥事件 B.A与C是对立事件
C.B与C是互斥事件 D.false
第Ⅱ卷(非选择题 共40分)
二、填空题:本题共计4小题,共计16分。
13.为迎接2022年北京冬奥会,某工厂生产了一批雪车,这批产品中按质量分为一等品,二等品,三等品.从这批雪车中随机抽取一件雪车检测,已知抽到不是三等品的概率为false,抽到一等品或三等品的概率为false,则抽到一等品的概率为___________.
14.有六个从左到右并排放置的盒子,现将若干个只有颜色不同的黑球?白球随机放入这六个盒子(每个盒子只能放入一个球),则事件“从左往右数,不管数到哪个盒子,总有黑球个数不少于白球个数”发生的概率为___________.
15.如图所示,由红?黄?蓝?白四种发光元件连接成倪红灯系统N,四种发光元件的工作相互独立,当四种发光元件均正常工作时,倪红灯系统N才能随机地发出亮丽的色彩,当某种元件出现故障时,倪红灯系统N在该处将出现短暂的黑幕现象,若某时刻出现两处黑幕现象,需从装有红?黄?蓝?白四种发光元件中(除颜色外没有区别)抽取两种相应的发光元件进行更换,则一次性从中随机抽取的两个恰为故障发光元件的概率为___________.
16.某学校团委在2021年春节前夕举办教师“学习强国”知识答题赛,其中高一年级的甲、乙两名教师组队参加答题赛,比赛共分两轮,每轮比赛甲、乙两人各答一题.已知甲答对每个题的概率为false,乙答对每个题的概率为false.假定甲、乙两人答题正确与否互不影响,则比赛结束时,甲、乙两人共答对三个题的概率为____________.
三、解答题:本题共计4小题,共计24分。
17.为了适应教育改革新形势,某实验高中新建实验楼、置办实验仪器、开设学生兴趣课堂,将分子生物学知识和技术引入其中,激发了广大学生的学习和科研热情.现已知该生物科研兴趣小组共有9名学生.在一次制作荧光标记小鼠模型时,将9名学生分成3组,每组3人.
(1)若将实验进程分为三个阶段,各个阶段由一个成员独立完成.现已知每个阶段用时1小时,每个阶段各成员成功率为false.若任意过程失败,则该实验须重新开始.求一个组在不超过4个小时完成实验任务的概率;
(2)现某小组3人代表学校组队外出参加生物实验竞赛,其中一项赛程为小鼠灌注实验.该赛程规则为:三人同时进行灌注实验,但每人只有一次机会,每个队员成功的概率均为false.若单个队员实验成功计2分,失败计1分.
①设小组总得分为false,求false的分布列与数学期望;
②主办方预计通过该赛程了解全国生物兴趣课程的开设情况.现从所有参赛队员中抽取false人成绩计入总得分,若总得分大于false的概率为false,求数列false的前15项和.
18.某学校高三年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在false内,发布成绩使用等级制,各等级划分标准见下表.
百分制
85分及以上
70分到84分
60分到69分
60分以下
等级
A
B
C
D
规定:A,B,C三级为合格等级,D为不合格等级.为了解该校高三年级学生身体素质情况,从中抽取了false名学生的原始成绩作为样本进行统计.按照false,false,false,false,false的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
(1)求false,false,false的值;
(2)根据频率分布直方图,求成绩的中位数(精确到0.1);
(3)在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.
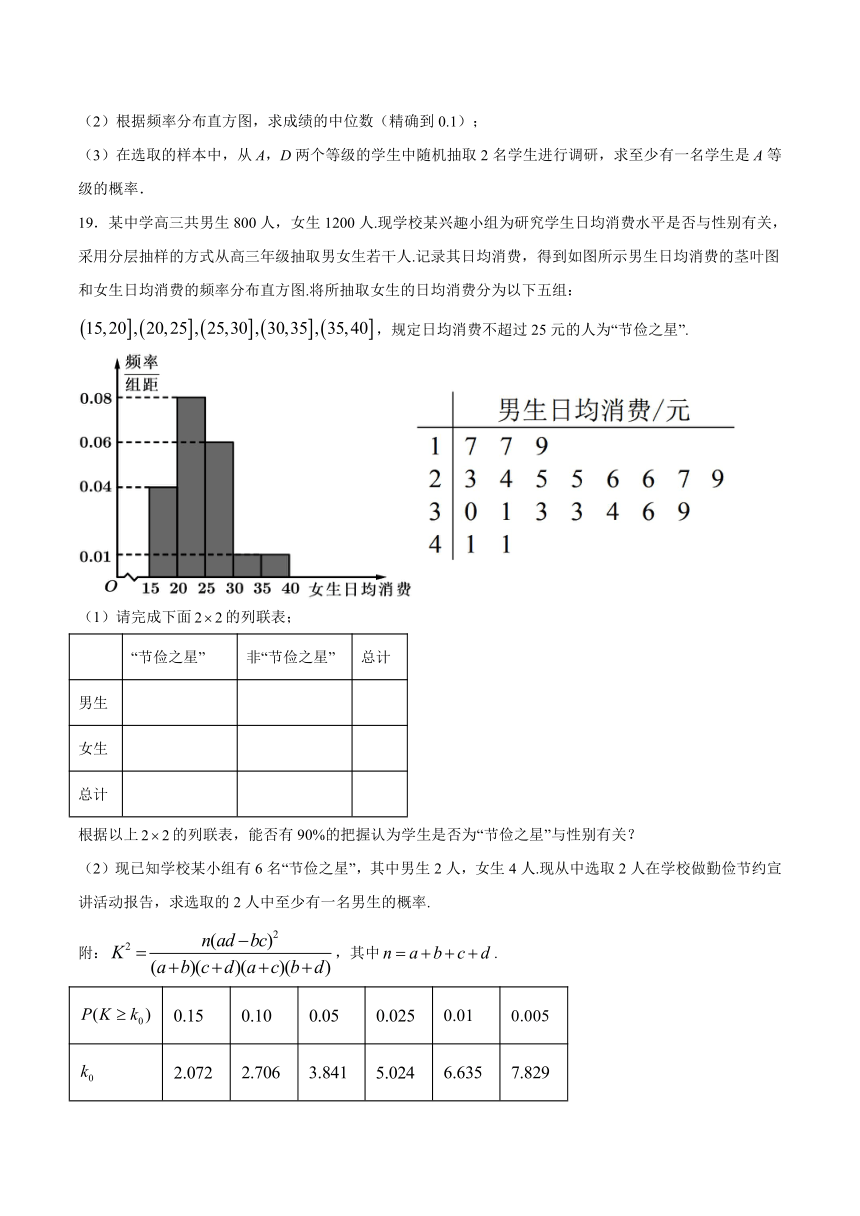
19.某中学高三共男生800人,女生1200人.现学校某兴趣小组为研究学生日均消费水平是否与性别有关,采用分层抽样的方式从高三年级抽取男女生若干人.记录其日均消费,得到如图所示男生日均消费的茎叶图和女生日均消费的频率分布直方图.将所抽取女生的日均消费分为以下五组:false,规定日均消费不超过25元的人为“节俭之星”.
(1)请完成下面false的列联表;
“节俭之星”
非“节俭之星”
总计
男生
女生
总计
根据以上false的列联表,能否有90%的把握认为学生是否为“节俭之星”与性别有关?
(2)现已知学校某小组有6名“节俭之星”,其中男生2人,女生4人.现从中选取2人在学校做勤俭节约宣讲活动报告,求选取的2人中至少有一名男生的概率.
附:false,其中false.
false
false
false
false
false
false
false
false
false
false
false
false
false
false
20.双败淘汰制是一种竞赛形式,与普通的单败淘汰制输掉一场即被淘汰不同,参赛者只有在输掉两场比赛后才丧失争夺冠军的可能.在双败淘汰制的比赛中,参赛者的数量一般是2的次方数,以保证每一轮都有偶数名参赛者.第一轮通过抽签,两人一组进行对阵,胜者进入胜者组,败者进入负者组.之后的每一轮直到最后一轮之前,胜者组的选手两人一组相互对阵,胜者进入下一轮,败者则降到负者组参加本轮负者组的第二阶段对阵;负者组的第一阶段,由之前负者组的选手(不包括本轮胜者组落败的选手)两人一组相互对阵,败者被淘汰(已经败两场),胜者进入第二阶段,分别对阵在本轮由胜者组中降组下来的选手,胜者进入下一轮,败者被淘汰.最后一轮,由胜者组最终获胜的选手(此前从未败过,记为false)对阵负者组最终获胜的选手(败过一场,记为false),若false胜则false获得冠军,若false胜则双方再次对阵,胜者获得冠军.某围棋赛事采用双败淘汰制,共有甲、乙、丙等8名选手参赛.第一轮对阵双方由随机抽签产生,之后每一场对阵根据赛事规程自动产生对阵双方,每场对阵没有平局.
(1)设“在第一轮对阵中,甲、乙、丙都不互为对手”为事件false,求false的概率;
(2)已知甲对阵其余7名选手获胜的概率均为false,解决以下问题:
①求甲恰在对阵三场后被淘汰的概率;
②若甲在第一轮获胜,设甲在该项赛事的总对阵场次为随机变量false,求false的分布列.
参考答案
1.D
【详解】
由题:“口香糖吃完时还剩2支香烟”说明:第四次取到的是口香糖,前三次中恰有两次口香糖一次香烟,记香烟为false,口香糖为false,进行四次取物,
基本事件总数为:false种
事件“口香糖吃完时还剩2支香烟”前四次取物顺序分为以下三种情况:
烟、糖、糖、糖:false种
糖、烟、糖、糖: false种
糖、糖、烟、糖:false种
包含的基本事件个数为:54,
所以,其概率为false
故选:D
2.B
【解析】
设false与false中至少有一个不闭合的事件为false与false至少有一个不闭合的事件为false,则false,所以灯亮的概率为false false, 故选B.
3.C
【详解】
由题知,要求每个盒子都不空,则3个盒子中放入小球的个数可分别为3,1,1或2,2,1,
若要求每个盒子中小球编号的奇偶性不同则只能是2,2,1,
且放入同一盒子中的两个小球必须是编号为一奇一偶,
故所求概率为false
故答案选C
4.C
【详解】
由题意,从6部专著中任选2部,共有false种不同的选法,
其中所选2部专著中恰有1部是汉、魏、晋、南北朝时期专著,共有false中选法,
所以所选2部专著中恰有1部是汉、魏、晋、南北朝时期专著的概率为false.
故选:C.
5.B
【详解】
“正面朝上恰好5次”是可能发生也可能不发生的事件,故该事件为随机事件.
故选:B
6.B
【详解】
根据题意,甲抛掷均匀硬币2017次,乙拋掷均匀硬币2016次,每次抛掷时出现正面的概率都是0.5,出现反面的概率也都是0.5
在①中,甲比乙多抛掷一次硬币,甲抛出正面次数比乙抛出正面次数多的概率为0.5,故①正确;
在②中,甲比乙多抛掷一次硬币,甲抛出反面次数比乙拋出正面次数少的概率不是0.5,故②错误;
在③中,甲抛掷均匀硬币2017次,甲抛出反面次数比甲抛出正面次数多的概率是0.5,故③正确;
在④中,乙抛掷均匀硬币2016次,乙抛出正面次数与乙抛出反面次数一样多的概率为false,故④错误,
故选:B
7.C
【详解】
事件false包含事件false,故false、false错误;
事件false与事件false没有相同的事件,故false正确,false错误.
故选:false.
8.B
【详解】
解:中奖概率false表示每一次抽奖中奖的可能性都是false,
故不论抽奖多少次,都可能一次也不中奖,
故选:B.
9.C
【详解】
对于A,至少摸出false个白球与摸出false个白球false个红球不是互斥事件;
对于B,至少摸出false个红球与摸出false个白球false个红球不是互斥事件;
对于C,摸出false个白球与摸出false个白球false个红球是互斥而不对立事件;
对于D,摸出false个白球或摸出false个红球与摸出个白球false个红球是互斥也是对立事件.
故选:C.
10.D
【详解】
“恰有一枚炮弹击中飞机”指第一枚击中第二枚没中或第一枚没中第二枚击中,“至少有一枚炮弹击中”包含两种情况:恰有一枚炮弹击中,两枚炮弹都击中.故A?D ,A∪C=D
B,D为互斥事件,B∩D=false;
A∪B=“两个飞机都击中或者都没击中”,B∪D为必然事件,这两者不相等
故选:D
11.B
【详解】
由题得不用现金支付的概率P=1-0.4-0.3=0.3.
故选B
12.D
【详解】
取出三件产品, A=“至多一件次品”, B=“至少一件次品”,
C=“三件产品全是次品”,D=“恰有一件次品”,
A与B能同时发生,所以A与B不是互斥事件,故A错误;
A与C不能同时发生,但A与C可以同时不发生,
故A与C不是对立事件,故B错误;
B与C能同时发生,所以B与C不是互斥事件,故C错误;
A与B能同时发生,此时有且只有一件次品,故false正确,
故选:D
13.false
【详解】
设抽到一等品?二等品?三等品的事件分别为false,false,false.则false,解得false,则抽到一等品的概率为false.
故答案为:0.78.
14.false
【详解】
每个盒子都有两种可能,所以基本事件有false种.符合条件的基本事件有:
①六黑有一种:黑黑黑黑黑黑;
②五黑一白有:黑黑黑黑黑白,黑黑黑黑白黑,黑黑黑白黑黑,黑黑白黑黑黑,黑白黑黑黑黑;共false种;
③四黑二白有:黑白黑白黑黑,黑白黑黑白黑,黑白黑黑黑白,黑黑白黑黑白,
黑黑白黑白黑,黑黑白白黑黑,黑黑黑白白黑,黑黑黑白黑白,黑黑黑黑白白;共false种;
④三黑三白有:黑黑黑白白白,黑黑白黑白白,黑白黑黑白白,黑白黑白黑白,
黑黑白白黑白;共false种;
所以,事件“从左往右数,不管数到哪个盒子,
总有黑球个数不少于白球个数”发生的概率为false.
故答案为:false.
15.false
【详解】
解:记红?黄?蓝?白四种发光元件分别为A,B,C,D
则从中随机抽取两个的所有情况为:AB,AC,AD,BC,CD,共6种
而更换的两个故障发光元件为其中一种情况
∴一次性从中随机抽取的两个恰为故障发光元件的概率为P=false.
故答案为:false
16.false
【详解】
由题意知:甲、乙两人共答对三个题的基本事件有{甲答对2个乙答对1个,甲答对1个乙答对2个},而甲答对每个题的概率为false,乙答对每个题的概率为false.
∴甲答对2个乙答对1个的概率为false,
甲答对1个乙答对2个的概率为false,
∴甲、乙两人共答对三个题的概率为false.
故答案为:false.
17.(1)false;(2)①分布列见解析;期望为5;②false.
【详解】
解:(1)一个组失误0次的概率为false;
仅第一步失误一次的概率为false,
则一个组在不超过4小时完成任务的概率为false.
(2)①随机变量false的可能取值为3,4,5,6,
false,false,
false,false.
则false的分布列为:
false
3
4
5
6
false
false
false
false
false
false.
②总得分大于false的概率为false,
则false的前15项和为false.
18.(1)false,false,false;(2)false;(3)false.
【详解】
(1)由题意,设样本容量为false,可得false,
则false,
(2)由频率分布直方图可得:false,false,
所以中位数位于false内,所以中位数为false.
(3)由茎叶图,可得false等级的学生有3人,false等级的学生有false,
记false等级的学生为false、false、false,false等级的学生为false、false、false、false、false,
从这8人中随机抽取2人,基本事件为:false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false,共有28个,
其中至少有一名是false等级的基本事件为:false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false,共有18个,
故所求的概率为false.
19.(1)列联表答案见解析,有90%把握认为学生是否为“节俭之星”与性别有关;(2)false.
【详解】
(1)由茎叶图可知此次抽样男生共20人,由于采用分层抽样的方式,抽取女生人数为30人.依题意:男“节俭之星”共7人,女“节俭之星”共18人,填表如下:
“节俭之星”
非“节俭之星”
总计
男生
7
13
20
女生
18
12
30
总计
25
25
50
从而false
故有90%把握认为学生是否为“节俭之星”与性别有关.
(2)记2名男生分别为A1,A2,记4名女生为B1,B2,B3,B4,则从这6名“节俭之星”选取2名的所有可能有:(A1,A2)(A1,B1)(A1,B2)(A1,B3)(A1,B4)
(A2,B1)(A2,B2)(A2,B3)(A2,B4)
(B1,B2)(B1,B3)(B1,B4)
(B2,B3)(B2,B4)
(B3,B4)
共15种,其中至少有1名男生的情况有9种,因此,所求概率为false
20.(1)false;(2)①false;②答案见解析.
【详解】
(1)8人平均分成四组,共有false种方法,
其中甲,乙,丙都不分在同一组的方法数为false,
所以false
false
(2)①甲恰在对阵三场后淘汰,这三场的结果依次是“胜,败,败”或“败,胜,败”,故所求的概率为false
false
②若甲在第一轮获胜,false.
当false时,表示甲在接下来的两场对阵都败,即false.
当false时,有两种情况:
(i)甲在接下来的3场比赛都胜,其概率为false;
(ii)甲4场对阵后被淘汰,表示甲在接下来的3场对阵1胜1败,且第4场败,
概率为false,
所以false
当false时,有两种情况:
(i)甲在接下来的2场对阵都胜,第4场败,概率为false;
(ii)甲在接下来的2场对阵1胜1败,第4场胜,第5场败,
概率为false;
所以false.
当false时,有两种情况:
(i)甲第2场胜,在接下来的3场对阵为“败,胜,胜”,
其概率为false;
(ii)甲第2场败,在接下来的4场对阵为“胜,胜,胜,败”,
其概率为false;
所以false.
当false时,甲在接下来的5场对阵为“败,胜,胜,胜,胜”,即false.
所以false的分布列为:
false
3
4
5
6
7
false
false
false
false
false
false
满分: 100分 时间: 60分钟
第Ⅰ卷(选择题 共60分)
单项选择题:本题共12小题,每题只有一个选项正确,每小题5分,共计60分。
1.吸烟有害健康,小明为了帮助爸爸戒烟,在爸爸包里放一个小盒子,里面随机摆放三支香烟和三支跟香烟外形完全一样的“戒烟口香糖”,并且和爸爸约定,每次想吸烟时,从盒子里任取一支,若取到口香糖则吃一支口香糖,不吸烟;若取到香烟,则吸一支烟,不吃口香糖,假设每次香烟和口香糖被取到的可能性相同,则“口香糖吃完时还剩2支香烟”的概率为( )
A.false B.false
C.false D.false
2.一个电路如图所示,A,B,C,D,E,F为6个开关,其闭合的概率为false,且是相互独立的,则灯亮的概率是( )
A.false B.false C.false D.false
3.将编号分别为1,2,3,4,5的5个小球分别放入3个不同的盒子中,每个盒子都不空,则每个盒子中所放小球的编号奇偶性均不相同的概率为
A.false B.false C.false D.false
4.我国古代有着辉煌的数学研究成果,其中《周髀算经》、《九章算术》、《海岛算经》、《数书九章》、《缉古算经》、《缀术》有丰富多彩的内容,是了解我国古代数学的重要文献,这6部专著中有4部产生于汉、魏、晋、南北朝时期.某中学拟从这6部专著中选择2部作为“数学文化”校本课程学习内容,则所选2部专著中恰有1部是汉、魏、晋、南北朝时期专著的概率为( )
A.false B.false C.false D.false
5.将一枚质地均匀的硬币向上抛掷10次,其中“正面朝上恰好有5次”是( )
A.必然事件 B.随机事件
C.不可能事件 D.无法确定
6.甲抛掷均匀硬币2017次,乙抛掷均匀硬币2016次,下列四个随机事件的概率是0.5的是( )
①甲抛出正面次数比乙抛出正面次数多;
②甲抛出反面次数比乙抛出正面次数少;
③甲抛出反面次数比甲抛出正面次数多;
④乙抛出正面次数与乙抛出反面次数一样多.
A.①② B.①③ C.②③ D.②④
7.从一批产品中取出三件产品,设事件A为“三件产品全不是次品”,事件B为“三件产品全是次品”,事件C为“三件产品至少有一件是次品”,则下列结论正确的是( )
A.B与C互斥 B.任何两个均互斥
C.A与C互斥 D.任何两个均不互斥
8.在北京消费季活动中,某商场为促销举行购物抽奖活动,规定购物消费每满200元就可以参加一次抽奖活动,中奖的概率为false.那么以下理解正确的是( )
A.某顾客抽奖10次,一定能中奖1次
B.某顾客抽奖10次,可能1次也没中奖
C.某顾客消费210元,一定不能中奖
D.某顾客消费1000元,至少能中奖1次
9.在一个袋子中放false个白球,false个红球,摇匀后随机摸出false个球,与“摸出false个白球false个红球”互斥而不对立的事件是( )
A.至少摸出false个白球 B.至少摸出false个红球
C.摸出false个白球 D.摸出false个白球或摸出false个红球
10.对空中飞行的飞机连续射击两次,每次发射一枚炮弹,设A=“两次都击中飞机”,B=“两次都没击中飞机”,C=“恰有一枚炮弹击中飞机”,D=“至少有一枚炮弹击中飞机”,下列关系不正确的是( )
A.A?D B.B∩D=false
C.A∪C=D D.A∪B=B∪D
11.若某群体中的成员只用现金支付的概率为0.4,既用现金支付也用非现金支付的概率为0.3,则不用现金支付的概率为( )
A.0.4 B.0.3 C.0.7 D.0.6
12.从一批产品中取出三件产品,设A=“至多一件次品”, B=“至少一件次品”,C=“三件产品全是次品”,D=“恰有一件次品”,则下列结论正确的是( )
A.A与B是互斥事件 B.A与C是对立事件
C.B与C是互斥事件 D.false
第Ⅱ卷(非选择题 共40分)
二、填空题:本题共计4小题,共计16分。
13.为迎接2022年北京冬奥会,某工厂生产了一批雪车,这批产品中按质量分为一等品,二等品,三等品.从这批雪车中随机抽取一件雪车检测,已知抽到不是三等品的概率为false,抽到一等品或三等品的概率为false,则抽到一等品的概率为___________.
14.有六个从左到右并排放置的盒子,现将若干个只有颜色不同的黑球?白球随机放入这六个盒子(每个盒子只能放入一个球),则事件“从左往右数,不管数到哪个盒子,总有黑球个数不少于白球个数”发生的概率为___________.
15.如图所示,由红?黄?蓝?白四种发光元件连接成倪红灯系统N,四种发光元件的工作相互独立,当四种发光元件均正常工作时,倪红灯系统N才能随机地发出亮丽的色彩,当某种元件出现故障时,倪红灯系统N在该处将出现短暂的黑幕现象,若某时刻出现两处黑幕现象,需从装有红?黄?蓝?白四种发光元件中(除颜色外没有区别)抽取两种相应的发光元件进行更换,则一次性从中随机抽取的两个恰为故障发光元件的概率为___________.
16.某学校团委在2021年春节前夕举办教师“学习强国”知识答题赛,其中高一年级的甲、乙两名教师组队参加答题赛,比赛共分两轮,每轮比赛甲、乙两人各答一题.已知甲答对每个题的概率为false,乙答对每个题的概率为false.假定甲、乙两人答题正确与否互不影响,则比赛结束时,甲、乙两人共答对三个题的概率为____________.
三、解答题:本题共计4小题,共计24分。
17.为了适应教育改革新形势,某实验高中新建实验楼、置办实验仪器、开设学生兴趣课堂,将分子生物学知识和技术引入其中,激发了广大学生的学习和科研热情.现已知该生物科研兴趣小组共有9名学生.在一次制作荧光标记小鼠模型时,将9名学生分成3组,每组3人.
(1)若将实验进程分为三个阶段,各个阶段由一个成员独立完成.现已知每个阶段用时1小时,每个阶段各成员成功率为false.若任意过程失败,则该实验须重新开始.求一个组在不超过4个小时完成实验任务的概率;
(2)现某小组3人代表学校组队外出参加生物实验竞赛,其中一项赛程为小鼠灌注实验.该赛程规则为:三人同时进行灌注实验,但每人只有一次机会,每个队员成功的概率均为false.若单个队员实验成功计2分,失败计1分.
①设小组总得分为false,求false的分布列与数学期望;
②主办方预计通过该赛程了解全国生物兴趣课程的开设情况.现从所有参赛队员中抽取false人成绩计入总得分,若总得分大于false的概率为false,求数列false的前15项和.
18.某学校高三年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在false内,发布成绩使用等级制,各等级划分标准见下表.
百分制
85分及以上
70分到84分
60分到69分
60分以下
等级
A
B
C
D
规定:A,B,C三级为合格等级,D为不合格等级.为了解该校高三年级学生身体素质情况,从中抽取了false名学生的原始成绩作为样本进行统计.按照false,false,false,false,false的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
(1)求false,false,false的值;
(2)根据频率分布直方图,求成绩的中位数(精确到0.1);
(3)在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.
19.某中学高三共男生800人,女生1200人.现学校某兴趣小组为研究学生日均消费水平是否与性别有关,采用分层抽样的方式从高三年级抽取男女生若干人.记录其日均消费,得到如图所示男生日均消费的茎叶图和女生日均消费的频率分布直方图.将所抽取女生的日均消费分为以下五组:false,规定日均消费不超过25元的人为“节俭之星”.
(1)请完成下面false的列联表;
“节俭之星”
非“节俭之星”
总计
男生
女生
总计
根据以上false的列联表,能否有90%的把握认为学生是否为“节俭之星”与性别有关?
(2)现已知学校某小组有6名“节俭之星”,其中男生2人,女生4人.现从中选取2人在学校做勤俭节约宣讲活动报告,求选取的2人中至少有一名男生的概率.
附:false,其中false.
false
false
false
false
false
false
false
false
false
false
false
false
false
false
20.双败淘汰制是一种竞赛形式,与普通的单败淘汰制输掉一场即被淘汰不同,参赛者只有在输掉两场比赛后才丧失争夺冠军的可能.在双败淘汰制的比赛中,参赛者的数量一般是2的次方数,以保证每一轮都有偶数名参赛者.第一轮通过抽签,两人一组进行对阵,胜者进入胜者组,败者进入负者组.之后的每一轮直到最后一轮之前,胜者组的选手两人一组相互对阵,胜者进入下一轮,败者则降到负者组参加本轮负者组的第二阶段对阵;负者组的第一阶段,由之前负者组的选手(不包括本轮胜者组落败的选手)两人一组相互对阵,败者被淘汰(已经败两场),胜者进入第二阶段,分别对阵在本轮由胜者组中降组下来的选手,胜者进入下一轮,败者被淘汰.最后一轮,由胜者组最终获胜的选手(此前从未败过,记为false)对阵负者组最终获胜的选手(败过一场,记为false),若false胜则false获得冠军,若false胜则双方再次对阵,胜者获得冠军.某围棋赛事采用双败淘汰制,共有甲、乙、丙等8名选手参赛.第一轮对阵双方由随机抽签产生,之后每一场对阵根据赛事规程自动产生对阵双方,每场对阵没有平局.
(1)设“在第一轮对阵中,甲、乙、丙都不互为对手”为事件false,求false的概率;
(2)已知甲对阵其余7名选手获胜的概率均为false,解决以下问题:
①求甲恰在对阵三场后被淘汰的概率;
②若甲在第一轮获胜,设甲在该项赛事的总对阵场次为随机变量false,求false的分布列.
参考答案
1.D
【详解】
由题:“口香糖吃完时还剩2支香烟”说明:第四次取到的是口香糖,前三次中恰有两次口香糖一次香烟,记香烟为false,口香糖为false,进行四次取物,
基本事件总数为:false种
事件“口香糖吃完时还剩2支香烟”前四次取物顺序分为以下三种情况:
烟、糖、糖、糖:false种
糖、烟、糖、糖: false种
糖、糖、烟、糖:false种
包含的基本事件个数为:54,
所以,其概率为false
故选:D
2.B
【解析】
设false与false中至少有一个不闭合的事件为false与false至少有一个不闭合的事件为false,则false,所以灯亮的概率为false false, 故选B.
3.C
【详解】
由题知,要求每个盒子都不空,则3个盒子中放入小球的个数可分别为3,1,1或2,2,1,
若要求每个盒子中小球编号的奇偶性不同则只能是2,2,1,
且放入同一盒子中的两个小球必须是编号为一奇一偶,
故所求概率为false
故答案选C
4.C
【详解】
由题意,从6部专著中任选2部,共有false种不同的选法,
其中所选2部专著中恰有1部是汉、魏、晋、南北朝时期专著,共有false中选法,
所以所选2部专著中恰有1部是汉、魏、晋、南北朝时期专著的概率为false.
故选:C.
5.B
【详解】
“正面朝上恰好5次”是可能发生也可能不发生的事件,故该事件为随机事件.
故选:B
6.B
【详解】
根据题意,甲抛掷均匀硬币2017次,乙拋掷均匀硬币2016次,每次抛掷时出现正面的概率都是0.5,出现反面的概率也都是0.5
在①中,甲比乙多抛掷一次硬币,甲抛出正面次数比乙抛出正面次数多的概率为0.5,故①正确;
在②中,甲比乙多抛掷一次硬币,甲抛出反面次数比乙拋出正面次数少的概率不是0.5,故②错误;
在③中,甲抛掷均匀硬币2017次,甲抛出反面次数比甲抛出正面次数多的概率是0.5,故③正确;
在④中,乙抛掷均匀硬币2016次,乙抛出正面次数与乙抛出反面次数一样多的概率为false,故④错误,
故选:B
7.C
【详解】
事件false包含事件false,故false、false错误;
事件false与事件false没有相同的事件,故false正确,false错误.
故选:false.
8.B
【详解】
解:中奖概率false表示每一次抽奖中奖的可能性都是false,
故不论抽奖多少次,都可能一次也不中奖,
故选:B.
9.C
【详解】
对于A,至少摸出false个白球与摸出false个白球false个红球不是互斥事件;
对于B,至少摸出false个红球与摸出false个白球false个红球不是互斥事件;
对于C,摸出false个白球与摸出false个白球false个红球是互斥而不对立事件;
对于D,摸出false个白球或摸出false个红球与摸出个白球false个红球是互斥也是对立事件.
故选:C.
10.D
【详解】
“恰有一枚炮弹击中飞机”指第一枚击中第二枚没中或第一枚没中第二枚击中,“至少有一枚炮弹击中”包含两种情况:恰有一枚炮弹击中,两枚炮弹都击中.故A?D ,A∪C=D
B,D为互斥事件,B∩D=false;
A∪B=“两个飞机都击中或者都没击中”,B∪D为必然事件,这两者不相等
故选:D
11.B
【详解】
由题得不用现金支付的概率P=1-0.4-0.3=0.3.
故选B
12.D
【详解】
取出三件产品, A=“至多一件次品”, B=“至少一件次品”,
C=“三件产品全是次品”,D=“恰有一件次品”,
A与B能同时发生,所以A与B不是互斥事件,故A错误;
A与C不能同时发生,但A与C可以同时不发生,
故A与C不是对立事件,故B错误;
B与C能同时发生,所以B与C不是互斥事件,故C错误;
A与B能同时发生,此时有且只有一件次品,故false正确,
故选:D
13.false
【详解】
设抽到一等品?二等品?三等品的事件分别为false,false,false.则false,解得false,则抽到一等品的概率为false.
故答案为:0.78.
14.false
【详解】
每个盒子都有两种可能,所以基本事件有false种.符合条件的基本事件有:
①六黑有一种:黑黑黑黑黑黑;
②五黑一白有:黑黑黑黑黑白,黑黑黑黑白黑,黑黑黑白黑黑,黑黑白黑黑黑,黑白黑黑黑黑;共false种;
③四黑二白有:黑白黑白黑黑,黑白黑黑白黑,黑白黑黑黑白,黑黑白黑黑白,
黑黑白黑白黑,黑黑白白黑黑,黑黑黑白白黑,黑黑黑白黑白,黑黑黑黑白白;共false种;
④三黑三白有:黑黑黑白白白,黑黑白黑白白,黑白黑黑白白,黑白黑白黑白,
黑黑白白黑白;共false种;
所以,事件“从左往右数,不管数到哪个盒子,
总有黑球个数不少于白球个数”发生的概率为false.
故答案为:false.
15.false
【详解】
解:记红?黄?蓝?白四种发光元件分别为A,B,C,D
则从中随机抽取两个的所有情况为:AB,AC,AD,BC,CD,共6种
而更换的两个故障发光元件为其中一种情况
∴一次性从中随机抽取的两个恰为故障发光元件的概率为P=false.
故答案为:false
16.false
【详解】
由题意知:甲、乙两人共答对三个题的基本事件有{甲答对2个乙答对1个,甲答对1个乙答对2个},而甲答对每个题的概率为false,乙答对每个题的概率为false.
∴甲答对2个乙答对1个的概率为false,
甲答对1个乙答对2个的概率为false,
∴甲、乙两人共答对三个题的概率为false.
故答案为:false.
17.(1)false;(2)①分布列见解析;期望为5;②false.
【详解】
解:(1)一个组失误0次的概率为false;
仅第一步失误一次的概率为false,
则一个组在不超过4小时完成任务的概率为false.
(2)①随机变量false的可能取值为3,4,5,6,
false,false,
false,false.
则false的分布列为:
false
3
4
5
6
false
false
false
false
false
false.
②总得分大于false的概率为false,
则false的前15项和为false.
18.(1)false,false,false;(2)false;(3)false.
【详解】
(1)由题意,设样本容量为false,可得false,
则false,
(2)由频率分布直方图可得:false,false,
所以中位数位于false内,所以中位数为false.
(3)由茎叶图,可得false等级的学生有3人,false等级的学生有false,
记false等级的学生为false、false、false,false等级的学生为false、false、false、false、false,
从这8人中随机抽取2人,基本事件为:false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false,共有28个,
其中至少有一名是false等级的基本事件为:false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false、false,共有18个,
故所求的概率为false.
19.(1)列联表答案见解析,有90%把握认为学生是否为“节俭之星”与性别有关;(2)false.
【详解】
(1)由茎叶图可知此次抽样男生共20人,由于采用分层抽样的方式,抽取女生人数为30人.依题意:男“节俭之星”共7人,女“节俭之星”共18人,填表如下:
“节俭之星”
非“节俭之星”
总计
男生
7
13
20
女生
18
12
30
总计
25
25
50
从而false
故有90%把握认为学生是否为“节俭之星”与性别有关.
(2)记2名男生分别为A1,A2,记4名女生为B1,B2,B3,B4,则从这6名“节俭之星”选取2名的所有可能有:(A1,A2)(A1,B1)(A1,B2)(A1,B3)(A1,B4)
(A2,B1)(A2,B2)(A2,B3)(A2,B4)
(B1,B2)(B1,B3)(B1,B4)
(B2,B3)(B2,B4)
(B3,B4)
共15种,其中至少有1名男生的情况有9种,因此,所求概率为false
20.(1)false;(2)①false;②答案见解析.
【详解】
(1)8人平均分成四组,共有false种方法,
其中甲,乙,丙都不分在同一组的方法数为false,
所以false
false
(2)①甲恰在对阵三场后淘汰,这三场的结果依次是“胜,败,败”或“败,胜,败”,故所求的概率为false
false
②若甲在第一轮获胜,false.
当false时,表示甲在接下来的两场对阵都败,即false.
当false时,有两种情况:
(i)甲在接下来的3场比赛都胜,其概率为false;
(ii)甲4场对阵后被淘汰,表示甲在接下来的3场对阵1胜1败,且第4场败,
概率为false,
所以false
当false时,有两种情况:
(i)甲在接下来的2场对阵都胜,第4场败,概率为false;
(ii)甲在接下来的2场对阵1胜1败,第4场胜,第5场败,
概率为false;
所以false.
当false时,有两种情况:
(i)甲第2场胜,在接下来的3场对阵为“败,胜,胜”,
其概率为false;
(ii)甲第2场败,在接下来的4场对阵为“胜,胜,胜,败”,
其概率为false;
所以false.
当false时,甲在接下来的5场对阵为“败,胜,胜,胜,胜”,即false.
所以false的分布列为:
false
3
4
5
6
7
false
false
false
false
false
false
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
