8.1成对数据的相关关系 课后小练-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(机构适用)(Word含答案)
文档属性
| 名称 | 8.1成对数据的相关关系 课后小练-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(机构适用)(Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 163.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 17:14:48 | ||
图片预览


文档简介
8.1成对数据的相关关系
1.在一次数学实验中,某同学运用图形计算器采集到如下一组数据:
x
-2
-1
1
2
3
y
0.24
0.51
2.02
3.98
80.2
在以下四个函数模型( a,b 为待定系数)中,最能反映 x,y 函数关系的是(??? )
A.?y=a+bx???????????????????????B.?y=a+bx???????????????????????C.?y=a+logbx???????????????????????D.?y=a+bx
2.“十三五”期间,我国大力实施就业优先政策,促进居民人均收入持续增长.下面散点图反映了2016-2020年我国居民人均可支配收入(单位:元)情况.根据图中提供的信息,下列判断不正确的是(??? )
A.?2016-2020年,全国居民人均可支配收入每年都超过20000元
B.?2017-2020年,全国居民人均可支配收入均逐年增加
C.?根据图中数据估计,2015年全国居民人均可支配收入可能高于20000元
D.?根据图中数据预测,2021年全国居民人均可支配收入一定大于30000元
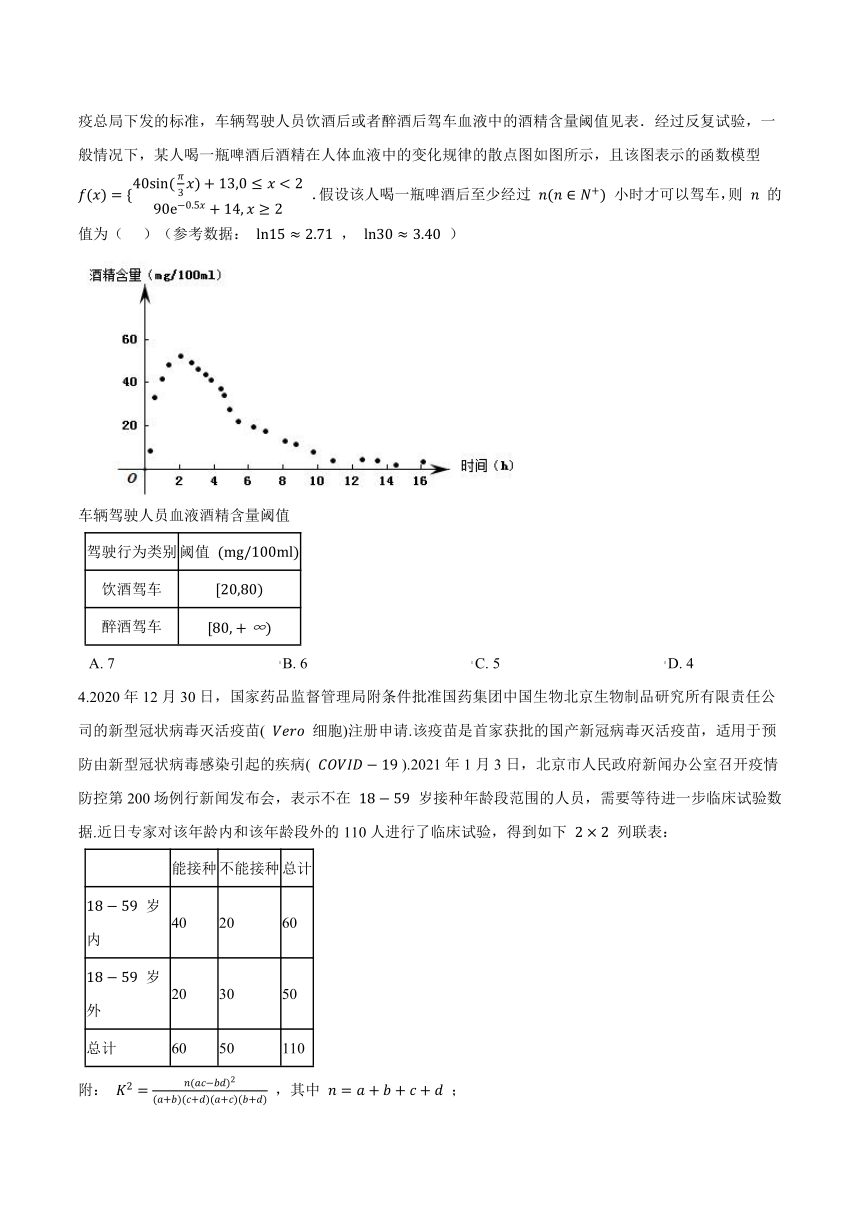
3.电影《流浪地球》中反复出现这样的人工语音:“道路千万条,安全第一条,行车不规范,亲人两行泪”,成为网络热句.讲的是“开车不喝酒,喝酒不开车”.2019年,公安部交通管理局下发《关于治理酒驾醉驾违法犯罪行为的指导意见》,对综合治理酒驾醉驾违法犯罪行为提出了新规定,根据国家质量监督检验检疫总局下发的标准,车辆驾驶人员饮酒后或者醉酒后驾车血液中的酒精含量阈值见表.经过反复试验,一般情况下,某人喝一瓶啤酒后酒精在人体血液中的变化规律的散点图如图所示,且该图表示的函数模型 f(x)={40sin(π3x)+13,0≤x<290e?0.5x+14,x≥2 .假设该人喝一瓶啤酒后至少经过 n(n∈N+) 小时才可以驾车,则 n 的值为(??? )(参考数据: ln15≈2.71 , ln30≈3.40 )
车辆驾驶人员血液酒精含量阈值
驾驶行为类别
阈值 (mg/100ml)
饮酒驾车
[20,80)
醉酒驾车
[80,+∞)
A.?7???????????????????????????????????????????B.?6???????????????????????????????????????????C.?5???????????????????????????????????????????D.?4
4.2020年12月30日,国家药品监督管理局附条件批准国药集团中国生物北京生物制品研究所有限责任公司的新型冠状病毒灭活疫苗( Vero 细胞)注册申请.该疫苗是首家获批的国产新冠病毒灭活疫苗,适用于预防由新型冠状病毒感染引起的疾病( COVID?19 ).2021年1月3日,北京市人民政府新闻办公室召开疫情防控第200场例行新闻发布会,表示不在 18?59 岁接种年龄段范围的人员,需要等待进一步临床试验数据.近日专家对该年龄内和该年龄段外的110人进行了临床试验,得到如下 2×2 列联表:
能接种
不能接种
总计
18?59 岁内
40
20
60
18?59 岁外
20
30
50
总计
60
50
110
附: K2=n(ac?bd)2(a+b)(c+d)(a+c)(b+d) ,其中 n=a+b+c+d ;
P(K2≥k)
0.050
0.010
0.001
k
3.841
6.635
10828
参照附表,得到的正确结论是(??? )
A.?在犯错误的概率不超过 0.1% 的前提下,认为“能接种与年龄段无关”
B.?在犯错误的概率不超过 0.1% 的前提下,认为“能接种与年龄段有关”
C.?有 99% 以上的把握认为“能接种与年龄段无关”
D.?有 99% 以上的把握认为“能接种与年龄段有关”
5.对四组数据进行统计,获得以下散点图,关于其线性相关系数比较,正确的是(? ?)
A.?r2C.?r46.“开车不喝酒,喝酒不开车.”近日,公安部交通管理局下发《关于2019年治理酒驾醉驾违法犯罪行为的指导意见》,对综合治理酒驾醉驾违法犯罪行为提出了新规定,根据国家质量监督检验检疫总局下发的标准,车辆驾驶人员饮酒后或者醉酒后驾车血液中的酒精含量阈值见表.经过反复试验,一般情况下,某人喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”见图,且图表所示的函数模型 f(x)={40sin(π3x)+13,0≤x<290?e?0.5x+14,x≥2 ,则该人喝一瓶啤酒后至少经过(??? )小时才可以驾车?(参考数据: ln15≈2.71,ln30≈3.40 )
车辆驾驶人员血液酒精含量阈值
驾驶行为类别
阈值( mg/100mL )
饮酒后驾车
≥20,<80
醉酒后驾车
≥80
A.?5???????????????????????????????????????????B.?6???????????????????????????????????????????C.?7???????????????????????????????????????????D.?8
7.观察下列各图形,
其中两个变量 x,y 具有相关关系的图是(??? )
A.?①②??????????????????????????????????????B.?①④??????????????????????????????????????C.?③④??????????????????????????????????????D.?③
8.某超市统计了最近5年的商品销售额与利润率数据,经计算相关系数 r=0.862 ,则下列判断正确的是(??? )
A.?商品销售额与利润率正相关,且具有较弱的相关关系
B.?商品销售额与利润率正相关,且具有较强的相关关系
C.?商品销售额与利润率负相关,且具有较弱的相关关系
D.?商品销售额与利润率负相关,且具有较强的相关关系
9.如图是九江市2019年4月至2020年3月每月最低气温与最高气温(℃)的折线统计图:已知每月最低气温与最高气温的线性相关系数r=0.83,则下列结论错误的是(??? )
?
A.?每月最低气温与最高气温有较强的线性相关性,且二者为线性正相关
B.?月温差(月最高气温﹣月最低气温)的最大值出现在10月
C.?9﹣12月的月温差相对于5﹣8月,波动性更大
D.?每月最高气温与最低气温的平均值在前6个月逐月增加
10.对于相关系数 r ,下列说法中正确的是(??? )
A.?r 越大,线性相关程度越强
B.?|r| 越小,线性相关程度越强
C.?|r| 越大,线性相关程度越弱, |r| 越小,线性相关程度越强
D.?|r|≤1 ,且 |r| 越接近 1 ,线性相关程度越强, |r| 越接近 0 ,线性相关程度越弱
11.在一组样本数据 (x1,y1) , (x2,y2) ,…, (xn,yn) ( n≥2 , x1 , x2 ,…, xn 互不相等)的散点图中,若所有样本点 (xi,yi)(i=1,2,…,n) 都在直线 y=?2x+100 上,则这组样本数据的样本相关系数为________.
12.为了对x,y两个变量进行统计分析,现根据两种线性模型分别计算出甲模型的相关指数为 R12=0.845 ,乙模型的相关指数为 R22=0.82 ,则________(填“甲”或“乙”)模型拟合的效果更好.
13.2020年是我国全面建成小康社会和打赢脱贫攻坚战的收官之年,某省为了坚决打嬴脱贫攻坚战,在100个贫闲村中,用简单随机抽样的方法抽取15个进行脱贫验收调查,调查得到的样本数据 (xi,yi) (i=1,2,???,15) ,其中 xi 和 yi 分別表示第i个贫困村中贫闲户的年平均收入(单位:万元)和产业扶贫资金投入数量(单位:万元),并计算得到 i=115xi=15 , i=115yi=750 , i=115(xi?x)2=0.82 , i=115(yi?y)2=1670 , i=115(xi?x)(yi?y)=35.3 .
附:相关系数 r=i=1n(xi?x)(yi?y)i=1n(xi?x)2i=1n(yi?y)2 , 1369.4≈37 .
(1)试估计该省贫困村的贫困户年平均收入.
(2)根据样本数据,求该省贫困村中贫困户年平均收入与产业扶贫资金投入的相关系数.(精确到0.01)
14.2020年是决胜全面建成小康社会、决战脱贫攻坚之年,面对新冠肺炎疫情和严重洪涝灾害的考验.党中央坚定如期完成脱贫攻坚目标决心不动摇,全党全社会戮力同心真抓实干,取得了积极成效.某贫困县为了响应国家精准扶贫的号召,特地承包了一块土地,已知土地的使用面积 x 与相应的管理时间 y 的关系如下表所示:
土地使用面积 x (单位:亩)
1
2
3
4
5
管理时间 y (单位:月)
8
11
14
24
23
并调查了某村300名村民参与管理的意愿,得到的部分数据如下表所示;
愿意参与管理
不愿意参与管理
男性村民
140
60
女性村民
40
参考公式: r=i=1n(xi?x)i=1n(xi?x)2i=1n(yi?y)2
参考数据: y=16,∑(y?y)2=206,515≈22.7
(1)做出散点图,判断土地使用面积 x 与管理时间 y 是否线性相关;并根据相关系数 r 说明相关关系的强弱.(若 |r|≥0.75 ,认为两个变量有很强的线性相关性, r 值精确到0.001) .
(2)若以该村的村民的性别与参与管理意风的情况估计贫困县的情况,且每位村民参与管理的意互不影响,则从该贫困县村民中任取3人,记取到不愿意参与管理的女性村民的人数为 X ,求 X 的分布列及数学期望.
15.2020年是脱贫攻坚的收官之年,国务院扶贫办确定的贫困县全部脱贫摘帽,脱贫攻坚取得重大胜利,为确保我国如期全面建成小康社会,实现第一个百年奋斗目标打下了坚实的基础在产业扶贫政策的大力支持下,西部某县新建了甲?乙两家玩具加工厂,加工同一型号的玩具质监部门随机抽检了两个厂的各100件玩具,在抽取中的200件玩具中,根据检测结果将它们分成“A”?“B”?“C”三个等级,A?B等级都是合格品,C等级是次品,统计结果如下表所示:
等级
A
B
C
频数
20
120
60
(表一)
厂家
合格品
次品
合计
甲
75
乙
35
合计
(表二)
在相关政策扶持下,确保每件合格品都有对口销售渠道,但从安全起见,所有的次品必须由原厂家自行销.
附: x2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d) ,其中 n=a+b+c+d .
P(x2≥x0)
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
x0
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(1)请根据所提供的数据,完成上面的2×2列联表(表二),并判断是否有95%的把握认为产品的合格率与厂家有关?
(2)每件玩具的生产成本为30元,A?B等级产品的出厂单价分别为60元?40元.另外已知每件次品的销毁费用为4元.若甲厂抽检的玩具中有10件为A等级,用样本的频率估计概率,试判断甲?乙两厂能否都能盈利,并说明理由.
---------------------------------------------------------------参考答案------------------------------------------------------------
1.【答案】 D 2.【答案】 D 3.【答案】 B 4.【答案】 D 5.【答案】 B 6.【答案】 B 7.【答案】 C 8.【答案】 B 9.【答案】 D 10.【答案】 D
11.【答案】 -1
12.【答案】 甲
13.【答案】 (1)解:该省贫困村的贫困户年平均收入的估计值为 115i=115xi=115×15=1 (万元),
(2)解:样本 (xi,yi)(i=1,2,???,15) 的相关系数为 r=i=115(xi?x)(yi?y)i=115(xi?x)2i=115(yi?y)2=35.30.82×1670 =35.31369.4≈35.337≈0.95 .(3)根据现有统计资料,各贫困村产业扶贫资金投入差异很大.为了确保完成脱贫攻坚战任务,准确地进行脱贫验收,请给出一种你认为更合理的抽样方法,并说明理由.
解:采用分层抽样,理由如下:由(2)知各地区贫困村的贫困户年平均收入与该村的产业投入资金有很强的正相关性,由于各贫困村产业扶贫资金投入差异很大,因此贫困村的贫困户年平均收入差异也很大,所以采用分层抽样的方法较好地保持了样本结构与总体结构得以执行,提高了样本的代表性,从而可以获得该省更准确的脱贫验收估计.
14.【答案】 (1)解:散点图如下图.
由散点图可知,管理时间 y 与土地使用面积 x 线性相关
依题意: x=1+2+3+4+55=3 ,又 y=16 ,
i=15(xi?x)(yi?y)=(?2)×8+(?1)×(?5)+0×(?2)+1×8+2×7=43 ,
i=15(xi?x)=(?2)+(?1)2+02+12+22=10 , i=15(yi?y)2=206 ,
则 r=i=1n(xi?x)(yi?y)i=1n(xi?x)i=1n(yi?y)=4310×206=432515≈4345.4≈0.947 ,
由于 0.947>0.75,
故管理时间 y 与土地使用面积 x 线性相关性较强
(2)解:由题知调查的300名村名中有不愿意参与管理的女性村民人数为 300?(140+40+60)=60 ,
该贫困县中任选一人,取到不愿意参与管理的女性树民的概率 p=60300=15 ,
则 X 可取 0,1,2,3 ,
P(X=0)=C310×(45)3=64125 ,
P(X=1)=C31×(45)2=48125 ,
P(X=2)=C32×(15)2×45=12125 ,
P(X=3)=C33×(15)3=1125 ,
即: X?B(3,15) , P(X=K)=C3k×(15)k×(45)3?k,k=0,1,2,3
X 的分布列
X
0
1
2
3
P
64125
48125
12125
1125
E(X)=0×64125+1×48125+2×12125+3×1125=35 ,即 E(X)=nP=3×15=35
15.【答案】 (1)解:2×2列联表如下
厂家
合格品
次品
合计
甲
75
25
100
乙
65
35
100
合计
140
60
200
K2=200×(75×35?25×65)2100×100×140×60≈2.38<3.841 ,
∴ 没有95%的把握认为产品的合格率与厂家有关.
(2)解:甲厂10件A等级,65件B等级,25件次品,
对于甲厂,单件产品利润X的可能取值为30,10, ?34 .
X的分布列如下:
X
30
10
?34
P
110
1320
14
∴E(X)=30×110+10×1320?34×14=1>0 ,
∴ 甲厂能盈利,
对于乙厂有10件A等级,55件B等级,35件次品,
对于乙厂,单位产品利润Y的可能取值为30,10, ?34 ,
Y分布列如下:
Y
30
10
?34
P
110
1120
720
∴E(Y)=30×110+10×1120?34×720=?175<0 ,乙不能盈利.
1.在一次数学实验中,某同学运用图形计算器采集到如下一组数据:
x
-2
-1
1
2
3
y
0.24
0.51
2.02
3.98
80.2
在以下四个函数模型( a,b 为待定系数)中,最能反映 x,y 函数关系的是(??? )
A.?y=a+bx???????????????????????B.?y=a+bx???????????????????????C.?y=a+logbx???????????????????????D.?y=a+bx
2.“十三五”期间,我国大力实施就业优先政策,促进居民人均收入持续增长.下面散点图反映了2016-2020年我国居民人均可支配收入(单位:元)情况.根据图中提供的信息,下列判断不正确的是(??? )
A.?2016-2020年,全国居民人均可支配收入每年都超过20000元
B.?2017-2020年,全国居民人均可支配收入均逐年增加
C.?根据图中数据估计,2015年全国居民人均可支配收入可能高于20000元
D.?根据图中数据预测,2021年全国居民人均可支配收入一定大于30000元
3.电影《流浪地球》中反复出现这样的人工语音:“道路千万条,安全第一条,行车不规范,亲人两行泪”,成为网络热句.讲的是“开车不喝酒,喝酒不开车”.2019年,公安部交通管理局下发《关于治理酒驾醉驾违法犯罪行为的指导意见》,对综合治理酒驾醉驾违法犯罪行为提出了新规定,根据国家质量监督检验检疫总局下发的标准,车辆驾驶人员饮酒后或者醉酒后驾车血液中的酒精含量阈值见表.经过反复试验,一般情况下,某人喝一瓶啤酒后酒精在人体血液中的变化规律的散点图如图所示,且该图表示的函数模型 f(x)={40sin(π3x)+13,0≤x<290e?0.5x+14,x≥2 .假设该人喝一瓶啤酒后至少经过 n(n∈N+) 小时才可以驾车,则 n 的值为(??? )(参考数据: ln15≈2.71 , ln30≈3.40 )
车辆驾驶人员血液酒精含量阈值
驾驶行为类别
阈值 (mg/100ml)
饮酒驾车
[20,80)
醉酒驾车
[80,+∞)
A.?7???????????????????????????????????????????B.?6???????????????????????????????????????????C.?5???????????????????????????????????????????D.?4
4.2020年12月30日,国家药品监督管理局附条件批准国药集团中国生物北京生物制品研究所有限责任公司的新型冠状病毒灭活疫苗( Vero 细胞)注册申请.该疫苗是首家获批的国产新冠病毒灭活疫苗,适用于预防由新型冠状病毒感染引起的疾病( COVID?19 ).2021年1月3日,北京市人民政府新闻办公室召开疫情防控第200场例行新闻发布会,表示不在 18?59 岁接种年龄段范围的人员,需要等待进一步临床试验数据.近日专家对该年龄内和该年龄段外的110人进行了临床试验,得到如下 2×2 列联表:
能接种
不能接种
总计
18?59 岁内
40
20
60
18?59 岁外
20
30
50
总计
60
50
110
附: K2=n(ac?bd)2(a+b)(c+d)(a+c)(b+d) ,其中 n=a+b+c+d ;
P(K2≥k)
0.050
0.010
0.001
k
3.841
6.635
10828
参照附表,得到的正确结论是(??? )
A.?在犯错误的概率不超过 0.1% 的前提下,认为“能接种与年龄段无关”
B.?在犯错误的概率不超过 0.1% 的前提下,认为“能接种与年龄段有关”
C.?有 99% 以上的把握认为“能接种与年龄段无关”
D.?有 99% 以上的把握认为“能接种与年龄段有关”
5.对四组数据进行统计,获得以下散点图,关于其线性相关系数比较,正确的是(? ?)
A.?r2
车辆驾驶人员血液酒精含量阈值
驾驶行为类别
阈值( mg/100mL )
饮酒后驾车
≥20,<80
醉酒后驾车
≥80
A.?5???????????????????????????????????????????B.?6???????????????????????????????????????????C.?7???????????????????????????????????????????D.?8
7.观察下列各图形,
其中两个变量 x,y 具有相关关系的图是(??? )
A.?①②??????????????????????????????????????B.?①④??????????????????????????????????????C.?③④??????????????????????????????????????D.?③
8.某超市统计了最近5年的商品销售额与利润率数据,经计算相关系数 r=0.862 ,则下列判断正确的是(??? )
A.?商品销售额与利润率正相关,且具有较弱的相关关系
B.?商品销售额与利润率正相关,且具有较强的相关关系
C.?商品销售额与利润率负相关,且具有较弱的相关关系
D.?商品销售额与利润率负相关,且具有较强的相关关系
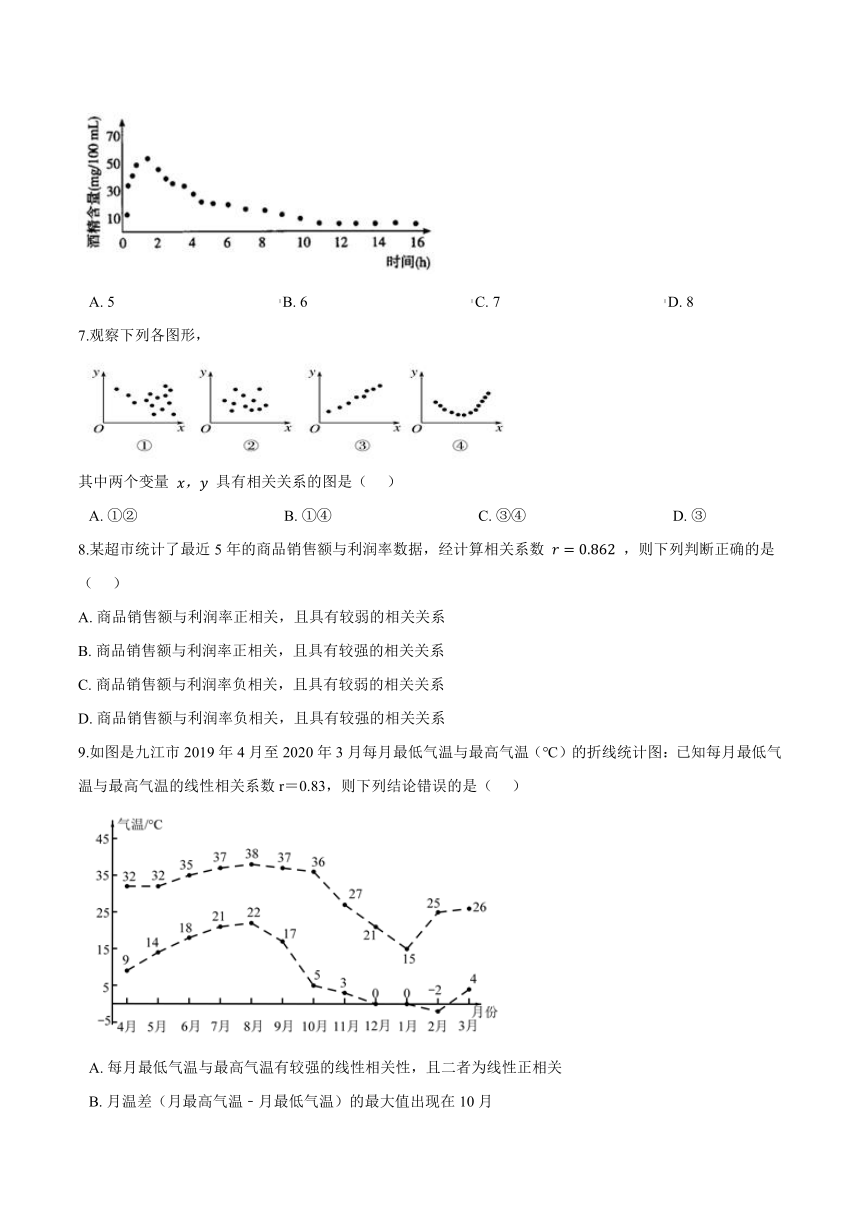
9.如图是九江市2019年4月至2020年3月每月最低气温与最高气温(℃)的折线统计图:已知每月最低气温与最高气温的线性相关系数r=0.83,则下列结论错误的是(??? )
?
A.?每月最低气温与最高气温有较强的线性相关性,且二者为线性正相关
B.?月温差(月最高气温﹣月最低气温)的最大值出现在10月
C.?9﹣12月的月温差相对于5﹣8月,波动性更大
D.?每月最高气温与最低气温的平均值在前6个月逐月增加
10.对于相关系数 r ,下列说法中正确的是(??? )
A.?r 越大,线性相关程度越强
B.?|r| 越小,线性相关程度越强
C.?|r| 越大,线性相关程度越弱, |r| 越小,线性相关程度越强
D.?|r|≤1 ,且 |r| 越接近 1 ,线性相关程度越强, |r| 越接近 0 ,线性相关程度越弱
11.在一组样本数据 (x1,y1) , (x2,y2) ,…, (xn,yn) ( n≥2 , x1 , x2 ,…, xn 互不相等)的散点图中,若所有样本点 (xi,yi)(i=1,2,…,n) 都在直线 y=?2x+100 上,则这组样本数据的样本相关系数为________.
12.为了对x,y两个变量进行统计分析,现根据两种线性模型分别计算出甲模型的相关指数为 R12=0.845 ,乙模型的相关指数为 R22=0.82 ,则________(填“甲”或“乙”)模型拟合的效果更好.
13.2020年是我国全面建成小康社会和打赢脱贫攻坚战的收官之年,某省为了坚决打嬴脱贫攻坚战,在100个贫闲村中,用简单随机抽样的方法抽取15个进行脱贫验收调查,调查得到的样本数据 (xi,yi) (i=1,2,???,15) ,其中 xi 和 yi 分別表示第i个贫困村中贫闲户的年平均收入(单位:万元)和产业扶贫资金投入数量(单位:万元),并计算得到 i=115xi=15 , i=115yi=750 , i=115(xi?x)2=0.82 , i=115(yi?y)2=1670 , i=115(xi?x)(yi?y)=35.3 .
附:相关系数 r=i=1n(xi?x)(yi?y)i=1n(xi?x)2i=1n(yi?y)2 , 1369.4≈37 .
(1)试估计该省贫困村的贫困户年平均收入.
(2)根据样本数据,求该省贫困村中贫困户年平均收入与产业扶贫资金投入的相关系数.(精确到0.01)
14.2020年是决胜全面建成小康社会、决战脱贫攻坚之年,面对新冠肺炎疫情和严重洪涝灾害的考验.党中央坚定如期完成脱贫攻坚目标决心不动摇,全党全社会戮力同心真抓实干,取得了积极成效.某贫困县为了响应国家精准扶贫的号召,特地承包了一块土地,已知土地的使用面积 x 与相应的管理时间 y 的关系如下表所示:
土地使用面积 x (单位:亩)
1
2
3
4
5
管理时间 y (单位:月)
8
11
14
24
23
并调查了某村300名村民参与管理的意愿,得到的部分数据如下表所示;
愿意参与管理
不愿意参与管理
男性村民
140
60
女性村民
40
参考公式: r=i=1n(xi?x)i=1n(xi?x)2i=1n(yi?y)2
参考数据: y=16,∑(y?y)2=206,515≈22.7
(1)做出散点图,判断土地使用面积 x 与管理时间 y 是否线性相关;并根据相关系数 r 说明相关关系的强弱.(若 |r|≥0.75 ,认为两个变量有很强的线性相关性, r 值精确到0.001) .
(2)若以该村的村民的性别与参与管理意风的情况估计贫困县的情况,且每位村民参与管理的意互不影响,则从该贫困县村民中任取3人,记取到不愿意参与管理的女性村民的人数为 X ,求 X 的分布列及数学期望.
15.2020年是脱贫攻坚的收官之年,国务院扶贫办确定的贫困县全部脱贫摘帽,脱贫攻坚取得重大胜利,为确保我国如期全面建成小康社会,实现第一个百年奋斗目标打下了坚实的基础在产业扶贫政策的大力支持下,西部某县新建了甲?乙两家玩具加工厂,加工同一型号的玩具质监部门随机抽检了两个厂的各100件玩具,在抽取中的200件玩具中,根据检测结果将它们分成“A”?“B”?“C”三个等级,A?B等级都是合格品,C等级是次品,统计结果如下表所示:
等级
A
B
C
频数
20
120
60
(表一)
厂家
合格品
次品
合计
甲
75
乙
35
合计
(表二)
在相关政策扶持下,确保每件合格品都有对口销售渠道,但从安全起见,所有的次品必须由原厂家自行销.
附: x2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d) ,其中 n=a+b+c+d .
P(x2≥x0)
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
x0
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(1)请根据所提供的数据,完成上面的2×2列联表(表二),并判断是否有95%的把握认为产品的合格率与厂家有关?
(2)每件玩具的生产成本为30元,A?B等级产品的出厂单价分别为60元?40元.另外已知每件次品的销毁费用为4元.若甲厂抽检的玩具中有10件为A等级,用样本的频率估计概率,试判断甲?乙两厂能否都能盈利,并说明理由.
---------------------------------------------------------------参考答案------------------------------------------------------------
1.【答案】 D 2.【答案】 D 3.【答案】 B 4.【答案】 D 5.【答案】 B 6.【答案】 B 7.【答案】 C 8.【答案】 B 9.【答案】 D 10.【答案】 D
11.【答案】 -1
12.【答案】 甲
13.【答案】 (1)解:该省贫困村的贫困户年平均收入的估计值为 115i=115xi=115×15=1 (万元),
(2)解:样本 (xi,yi)(i=1,2,???,15) 的相关系数为 r=i=115(xi?x)(yi?y)i=115(xi?x)2i=115(yi?y)2=35.30.82×1670 =35.31369.4≈35.337≈0.95 .(3)根据现有统计资料,各贫困村产业扶贫资金投入差异很大.为了确保完成脱贫攻坚战任务,准确地进行脱贫验收,请给出一种你认为更合理的抽样方法,并说明理由.
解:采用分层抽样,理由如下:由(2)知各地区贫困村的贫困户年平均收入与该村的产业投入资金有很强的正相关性,由于各贫困村产业扶贫资金投入差异很大,因此贫困村的贫困户年平均收入差异也很大,所以采用分层抽样的方法较好地保持了样本结构与总体结构得以执行,提高了样本的代表性,从而可以获得该省更准确的脱贫验收估计.
14.【答案】 (1)解:散点图如下图.
由散点图可知,管理时间 y 与土地使用面积 x 线性相关
依题意: x=1+2+3+4+55=3 ,又 y=16 ,
i=15(xi?x)(yi?y)=(?2)×8+(?1)×(?5)+0×(?2)+1×8+2×7=43 ,
i=15(xi?x)=(?2)+(?1)2+02+12+22=10 , i=15(yi?y)2=206 ,
则 r=i=1n(xi?x)(yi?y)i=1n(xi?x)i=1n(yi?y)=4310×206=432515≈4345.4≈0.947 ,
由于 0.947>0.75,
故管理时间 y 与土地使用面积 x 线性相关性较强
(2)解:由题知调查的300名村名中有不愿意参与管理的女性村民人数为 300?(140+40+60)=60 ,
该贫困县中任选一人,取到不愿意参与管理的女性树民的概率 p=60300=15 ,
则 X 可取 0,1,2,3 ,
P(X=0)=C310×(45)3=64125 ,
P(X=1)=C31×(45)2=48125 ,
P(X=2)=C32×(15)2×45=12125 ,
P(X=3)=C33×(15)3=1125 ,
即: X?B(3,15) , P(X=K)=C3k×(15)k×(45)3?k,k=0,1,2,3
X 的分布列
X
0
1
2
3
P
64125
48125
12125
1125
E(X)=0×64125+1×48125+2×12125+3×1125=35 ,即 E(X)=nP=3×15=35
15.【答案】 (1)解:2×2列联表如下
厂家
合格品
次品
合计
甲
75
25
100
乙
65
35
100
合计
140
60
200
K2=200×(75×35?25×65)2100×100×140×60≈2.38<3.841 ,
∴ 没有95%的把握认为产品的合格率与厂家有关.
(2)解:甲厂10件A等级,65件B等级,25件次品,
对于甲厂,单件产品利润X的可能取值为30,10, ?34 .
X的分布列如下:
X
30
10
?34
P
110
1320
14
∴E(X)=30×110+10×1320?34×14=1>0 ,
∴ 甲厂能盈利,
对于乙厂有10件A等级,55件B等级,35件次品,
对于乙厂,单位产品利润Y的可能取值为30,10, ?34 ,
Y分布列如下:
Y
30
10
?34
P
110
1120
720
∴E(Y)=30×110+10×1120?34×720=?175<0 ,乙不能盈利.
