8.2一元线性回归模型及其应用 课后小练-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(机构适用)(Word含答案)
文档属性
| 名称 | 8.2一元线性回归模型及其应用 课后小练-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(机构适用)(Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 67.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 17:15:10 | ||
图片预览


文档简介
8.2一元线性回归模型及其应用
1.某地以“绿水青山就是金山银山”理念为引导,推进绿色发展,现要订购一批苗木,苗木长度与售价如下表:
苗木长度 x (厘米)
38
48
58
68
78
88
售价 y (元)
16.8
18.8
20.8
22.8
24
258.8
由表可知,苗木长度 x (厘米)与售价 y (元)之间存在线性相关关系,回归方程为 y=0.2x+a ,则当苗木长度为150厘米时,售价大约为(??? )
A.?33.3?????????????????????????????????????B.?35.5?????????????????????????????????????C.?38.9?????????????????????????????????????D.?41.5
2.某实验室研发新冠疫苗,试验中需对 x , y 两项指标进行对照试验.已经进行的连续五次试验所测得的指标数据如下表:
x
110
115
120
125
130
y
85
89
90
92
94
已知 y 与 x 具有线性相关关系,利用上表中的五组数据求得回归直线方程为 y=bx+a .根据该回归方程,预测下一次试验中当 x=150 时, y=106.2 ,则 b 的值为(??? )
A.?0.48??????????????????????????????????????B.?0.5??????????????????????????????????????C.?0.52??????????????????????????????????????D.?0.54
3.给出下列说法:
①回归直线 y=bx+a 恒过样本点的中心 (x,y) ,且至少过一个样本点;②两个变量相关性越强,则相关系数 |r| 就越接近1;③将一组数据的每个数据都加一个相同的常数后,方差不变;④在回归直线方程 y=2?0.5x 中,当解释变量 x 增加一个单位时,预报变量 y 平均减少0.5个单位.
其中说法正确的是(??? )
A.?①②④?????????????????????????????????B.?②③④?????????????????????????????????C.?①③④?????????????????????????????????D.?②④
4.蟋蟀鸣叫可以说是大自然优美、和谐的音乐,殊不知蟋蟀鸣叫的频率x(每分钟鸣叫的次数)与气温y(单位:℃)存在着较强的线性相关关系.某地观测人员根据下表的观测数据,建立了y关于x的线性回归方程 y=0.25x+k ,
x(次数/分钟)
20
30
40
50
60
y(℃)
25
27.5
29
32.5
36
则当蟋蟀每分钟鸣叫56次时,该地当时的气温预报值为(??? )
A.?33℃???????????????????????????????????B.?34℃???????????????????????????????????C.?35℃???????????????????????????????????D.?35.5℃
5.已知 y 与 x 之间的线性回归方程为 y=1.6x+21 ,其样本点的中心为 (x,37) ,样本数据中 x 的输出取值依次为2,8,6,14, m ,则 m= (??? )
A.?12?????????????????????????????????????????B.?16?????????????????????????????????????????C.?18?????????????????????????????????????????D.?20
6.根据如下样本数据,得到回归直线方程 y=bx+a ,则(??? )
x
3
4
5
6
7
8
y
-3.0
-2.0
0.5
-0.5
2.5
4.0
A.?a>0 , b>0?????????????????B.?a>0 , b<0?????????????????C.?a<0 , b>0?????????????????D.?a<0 , b<0
7.调查了某地若干户家庭的年收入 x (单位:万元)和年饮食支出 y (单位:万元),调查显示年收入 x 与年饮食支出 y 具有线性相关关系,并由调查数据得到 y 对 x 的回归直线方程: i=1nxiyi?nxy=184?10×8×2=24 .由回归直线方程可知,家庭年收入每增加1万元,则预计年饮食支出平均增加(??? )
A.?0.067万元?????????????????????????B.?0.254 万元?????????????????????????C.?0.321万元?????????????????????????D.?0.575万元
8.某商铺统计了今年5个月的用电量y(单位:10kw/h)与月份x的对应数据,列表如下:
x
2
4
5
6
8
y
30
40
57
a
69
根据表中数据求出 y 关于 x 的线性回归方程为 y=6.5x+17.5 ,则上表中 a 的值为(??? )
A.?50????????????????????????????????????????B.?54????????????????????????????????????????C.?56.5????????????????????????????????????????D.?64
9.下列说法:
①若线性回归方程为 y=3x?5 ,则当变量x增加一个单位时,y一定增加3个单位;②将一组数据中的每个数据都加上同一个常数后,方差不会改变;③线性回归直线方程 y=bx+a 必过点 (x,y) ;④抽签法属于简单随机抽样,而随机数表法属于系统抽样,
其中错误的说法是(??? )
A.?①③??????????????????????????????????B.?②③④??????????????????????????????????C.?①②④??????????????????????????????????D.?①④
10.某产品的宣传费用x(万元)与销售额y(万元)的统计数据如下表所示:
宣传费用x(万元)
2
3
4
5
销售额y(万元)
24
30
42
50
根据上表可得回归方程 y=9x+a ,则宣传费用为6万元时,销售额约为________万元.
11.蟋蟀鸣叫可以说是大自然优美?和谐的音乐,蟋蟀鸣叫的频率 y (每分钟鸣叫的次数)与气温 x (单位: ?C )存在着较强的线性相关关系.某地研究人员根据当地的气温和蟋蟀鸣叫的频率得到了如下数据:
x(?C)
21
22
23
24
25
26
27
y (次数/分钟)
24
28
31
39
43
47
54
利用上表中的数据求得回归直线方程为 y=bx+a ,若利用该方程知,当该地的气温为 30?C 时,蟋蟀每分钟鸣叫次数的预报值为68,则 b 的值为________.
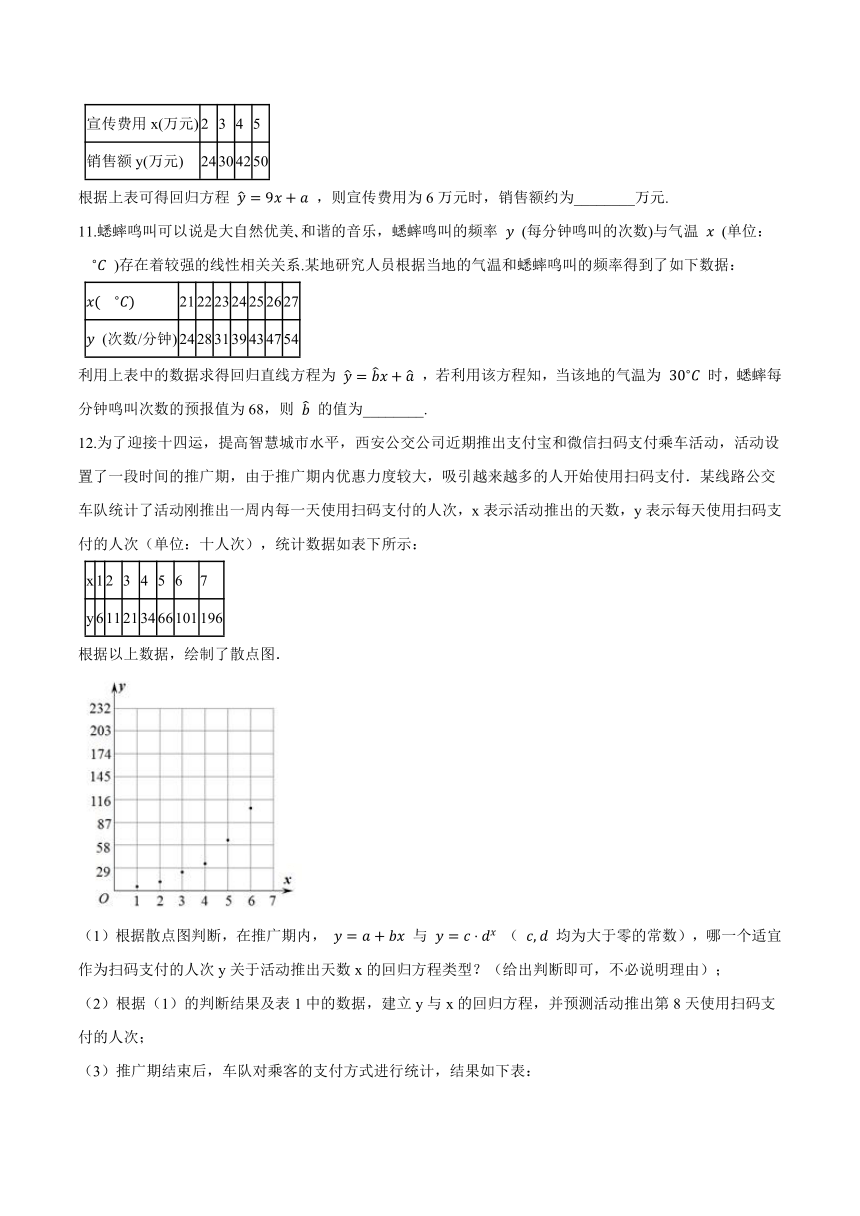
12.为了迎接十四运,提高智慧城市水平,西安公交公司近期推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,x表示活动推出的天数,y表示每天使用扫码支付的人次(单位:十人次),统计数据如表下所示:
x
1
2
3
4
5
6
7
y
6
11
21
34
66
101
196
根据以上数据,绘制了散点图.
(1)根据散点图判断,在推广期内, y=a+bx 与 y=c?dx ( c,?d 均为大于零的常数),哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表1中的数据,建立y与x的回归方程,并预测活动推出第8天使用扫码支付的人次;
(3)推广期结束后,车队对乘客的支付方式进行统计,结果如下表:
支付方式
现金
乘车卡
扫码
比例
10%
60%
30%
西安公交六公司车队为缓解周边居民出行压力,以90万元的单价购进了一批新车,根据以往的经验可知,每辆车每个月的运营成本约为0.66万元.已知该线路公交车票价为2元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受8折优惠,扫码支付的乘客随机优惠,根据统计结果得知,使用扫码支付的乘客中有 16 的概率享受7折优惠,有 13 的概率享受8折优惠,有 12 的概率享受9折优惠.预计该车队每辆车每个月有2万人次乘车,根据所给数据以事件发生的频率作为相应事件发生的概率,在不考虑其它因素的条件下,按照上述收费标准,请你估计这批车辆需要几年(结果取整数年)才能盈利?
参考数据:
y
v
i=17xiyi
i=17xivi
100.54
62.14
1.54
2535
50.12
3.47
其中其中 vi=lgyi , v=17i=17vi ,
参考公式:对于一组数据 (u1,?v1) , (u2,?v2) ,…, (un,?vn) ,其回归直线 v=α+βu 的斜率和截距的最小二乘估计公式分别为: β=i=1nuivi?nu?vi=1nui2?nu2 , α=v?βu .
13.某公司为一所山区小学安装了价值2万元的一台饮用水净化设备,每年都要为这台设备支出保养维修费用,我们称之为设备年度保养维修费.下表是该公司第 x 年为这台设备支出的年度保养维修费 y (单位:千元)的部分数据:
x
2
3
4
5
6
y
2.1
3.4
5.9
6.6
7.0
画出散点图如下:
通过计算得 y 与 x 的相关系数 r≈0.96 .由散点图和相关系数 r 的值可知, y 与 x 的线性相关程度很高.
附: b=i=1n(xi?x)(yi?y)i=1n(xi?x)2 , a=y?bx .
(1)建立 y 关于 x 的线性回归方程 y=bx+a ;
(2)若设备年度保养维修费不超过1.93万元就称该设备当年状态正常,根据(1)得到的线性回归方程,估计这台设备有多少年状态正常?
14.某种机械设备随着使用年限的增加,它的使用功能逐渐减退,使用价值逐年减少,通常把它使用价值逐年减少的“量”换算成费用,称之为“失效费”.某种机械设备的使用年限 x (单位:年)与失效费 y (单位:万元)的统计数据如下表所示:
使用年限 x (单位:年)
1
2
3
4
5
6
7
失效费 y (单位:万元)
2.90
3.30
3.60
4.40
4.80
5.20
5.90
(Ⅰ)由上表数据可知,可用线性回归模型拟合 y 与 x 的关系.请用相关系数加以说明;(精确到0.01)
(Ⅱ)求出 y 关于 x 的线性回归方程,并估算该种机械设备使用10年的失效费.
参考公式:相关系数 r=i=1n(xi?x)(yi?y)i=1n(xi?x)2i=1n(yi?y)2 .
线性回归方程 y=bx+a 中斜率和截距最小二乘估计计算公式: b=i=1n(xi?x)(yi?y)i=1n(xi?x)2 , a=y?bx .
参考数据: i=17(xi?x)(yi?y)=14.00 , i=17(yi?y)2=7.08 , 198.24≈14.10 .
---------------------------------------------------------------参考答案------------------------------------------------------------
1.【答案】 C 2.【答案】 D 3.【答案】 B 4.【答案】 B 5.【答案】 D 6.【答案】 C 7.【答案】 B 8.【答案】 B 9.【答案】 D 10.【答案】 59
11.【答案】 5
12.【答案】 (1)根据散点图判断,在推广期内, y=c?dx ( c,?d 均为大于零的常数),适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型;
(2)根据(1)的判断结果 y=c?dx ,两边取对数得: lgy=lgc+lgd?x ,
其中 vi=lgyi , v=17i=17vi=1.54 , i=17xivi=50.12 , x=4 , i=17xi2=140 ,
∴β=lgd=i=17xivi?nx?vi=1nxi2?nx2=0.25 , α=lgc=v?βx=0.54 ,
∴lgy=0.54+0.25x , ∴y=100.54+0.25?x=3.47×100.25x .
当 x=8 时, y=100.54+0.25?8=3.47×102=347 ,
∴活动推出第8天使用扫码支付的人次为3470人;
(3)设一名乘客一次乘车的费用为 ξ 元,
由题意知: ξ 所有可能取值为:1.4,1.6,1.8,2,
∴P(ξ=1.4)=0.3×16=0.05 , P(ξ=1.6)=0.6+0.3×13=0.7 , P(ξ=1.8)=0.3×12=0.15 , P(ξ=2)=0.1 ,
∴E(ξ)=1.4×0.05+1.6×0.7+1.8×0.15+2×0.1=1.66 ,
假设这批车需要 n(n∈N?) 年才能开始盈利,则 1.66×2×12×n≥90+0.66×12×n ,
解得: n≥2.82 ,∴需要3年才能盈利.
13.【答案】 (1)解: x=15×(2+3+4+5+6)=4 ,
y=15×(2.1+3.4+5.9+6.6+7)=5 .
b=i=15(xi?x)(yi?y)i=15(xi?x)2=1310=1.3 .
∴a=y?bx=5?1.3×4=?0.2 .
∴ 线性回归方程为 y=1.3x?0.2 .
(2)解:设这台设备有 x 年状态正常,由已知得 y≤19.3 ,即 1.3x?0.2≤19.3 .
解 1.3x?0.2≤19.3 得 x≤15 .
∴ 估计该设备有 15 年状态正常
14.【答案】 解:(Ⅰ)由题意,知 x=1+2+3+4+5+6+77=4 , y=2.90+3.30+3.60+4.40+4.80+5.20+5.907=4.30 ,
i=17(xi?x)2=(1?4)2+(2?4)2+(3?4)2+(4?4)2+(5?4)2+(6?4)2+(7?4)2=28 .
∴结合参考数据知: r=14.0028×7.08=14.00198.24≈14.0014.10≈0.99 .
因为 y 与 x 的相关系数近似为0.99,所以 y 与 x 的线性相关程度相当大,从而可以用线性回归模型拟合 y 与 x 的关系.
(Ⅱ)∵ b=i=17(xi?x)(yi?y)i=17(xi?x)2=1428=0.5 ,
∴ a=y?bx=4.3?0.5×4=2.3 .
∴ y 关于 x 的线性回归方程为 y=0.5x+2.3 ,将 x=10 代入线性回归方程,得 y=0.5×10+2.3=7.3 .
∴估算该种机械设备使用10年的失效费为7.3万元.
1.某地以“绿水青山就是金山银山”理念为引导,推进绿色发展,现要订购一批苗木,苗木长度与售价如下表:
苗木长度 x (厘米)
38
48
58
68
78
88
售价 y (元)
16.8
18.8
20.8
22.8
24
258.8
由表可知,苗木长度 x (厘米)与售价 y (元)之间存在线性相关关系,回归方程为 y=0.2x+a ,则当苗木长度为150厘米时,售价大约为(??? )
A.?33.3?????????????????????????????????????B.?35.5?????????????????????????????????????C.?38.9?????????????????????????????????????D.?41.5
2.某实验室研发新冠疫苗,试验中需对 x , y 两项指标进行对照试验.已经进行的连续五次试验所测得的指标数据如下表:
x
110
115
120
125
130
y
85
89
90
92
94
已知 y 与 x 具有线性相关关系,利用上表中的五组数据求得回归直线方程为 y=bx+a .根据该回归方程,预测下一次试验中当 x=150 时, y=106.2 ,则 b 的值为(??? )
A.?0.48??????????????????????????????????????B.?0.5??????????????????????????????????????C.?0.52??????????????????????????????????????D.?0.54
3.给出下列说法:
①回归直线 y=bx+a 恒过样本点的中心 (x,y) ,且至少过一个样本点;②两个变量相关性越强,则相关系数 |r| 就越接近1;③将一组数据的每个数据都加一个相同的常数后,方差不变;④在回归直线方程 y=2?0.5x 中,当解释变量 x 增加一个单位时,预报变量 y 平均减少0.5个单位.
其中说法正确的是(??? )
A.?①②④?????????????????????????????????B.?②③④?????????????????????????????????C.?①③④?????????????????????????????????D.?②④
4.蟋蟀鸣叫可以说是大自然优美、和谐的音乐,殊不知蟋蟀鸣叫的频率x(每分钟鸣叫的次数)与气温y(单位:℃)存在着较强的线性相关关系.某地观测人员根据下表的观测数据,建立了y关于x的线性回归方程 y=0.25x+k ,
x(次数/分钟)
20
30
40
50
60
y(℃)
25
27.5
29
32.5
36
则当蟋蟀每分钟鸣叫56次时,该地当时的气温预报值为(??? )
A.?33℃???????????????????????????????????B.?34℃???????????????????????????????????C.?35℃???????????????????????????????????D.?35.5℃
5.已知 y 与 x 之间的线性回归方程为 y=1.6x+21 ,其样本点的中心为 (x,37) ,样本数据中 x 的输出取值依次为2,8,6,14, m ,则 m= (??? )
A.?12?????????????????????????????????????????B.?16?????????????????????????????????????????C.?18?????????????????????????????????????????D.?20
6.根据如下样本数据,得到回归直线方程 y=bx+a ,则(??? )
x
3
4
5
6
7
8
y
-3.0
-2.0
0.5
-0.5
2.5
4.0
A.?a>0 , b>0?????????????????B.?a>0 , b<0?????????????????C.?a<0 , b>0?????????????????D.?a<0 , b<0
7.调查了某地若干户家庭的年收入 x (单位:万元)和年饮食支出 y (单位:万元),调查显示年收入 x 与年饮食支出 y 具有线性相关关系,并由调查数据得到 y 对 x 的回归直线方程: i=1nxiyi?nxy=184?10×8×2=24 .由回归直线方程可知,家庭年收入每增加1万元,则预计年饮食支出平均增加(??? )
A.?0.067万元?????????????????????????B.?0.254 万元?????????????????????????C.?0.321万元?????????????????????????D.?0.575万元
8.某商铺统计了今年5个月的用电量y(单位:10kw/h)与月份x的对应数据,列表如下:
x
2
4
5
6
8
y
30
40
57
a
69
根据表中数据求出 y 关于 x 的线性回归方程为 y=6.5x+17.5 ,则上表中 a 的值为(??? )
A.?50????????????????????????????????????????B.?54????????????????????????????????????????C.?56.5????????????????????????????????????????D.?64
9.下列说法:
①若线性回归方程为 y=3x?5 ,则当变量x增加一个单位时,y一定增加3个单位;②将一组数据中的每个数据都加上同一个常数后,方差不会改变;③线性回归直线方程 y=bx+a 必过点 (x,y) ;④抽签法属于简单随机抽样,而随机数表法属于系统抽样,
其中错误的说法是(??? )
A.?①③??????????????????????????????????B.?②③④??????????????????????????????????C.?①②④??????????????????????????????????D.?①④
10.某产品的宣传费用x(万元)与销售额y(万元)的统计数据如下表所示:
宣传费用x(万元)
2
3
4
5
销售额y(万元)
24
30
42
50
根据上表可得回归方程 y=9x+a ,则宣传费用为6万元时,销售额约为________万元.
11.蟋蟀鸣叫可以说是大自然优美?和谐的音乐,蟋蟀鸣叫的频率 y (每分钟鸣叫的次数)与气温 x (单位: ?C )存在着较强的线性相关关系.某地研究人员根据当地的气温和蟋蟀鸣叫的频率得到了如下数据:
x(?C)
21
22
23
24
25
26
27
y (次数/分钟)
24
28
31
39
43
47
54
利用上表中的数据求得回归直线方程为 y=bx+a ,若利用该方程知,当该地的气温为 30?C 时,蟋蟀每分钟鸣叫次数的预报值为68,则 b 的值为________.
12.为了迎接十四运,提高智慧城市水平,西安公交公司近期推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,x表示活动推出的天数,y表示每天使用扫码支付的人次(单位:十人次),统计数据如表下所示:
x
1
2
3
4
5
6
7
y
6
11
21
34
66
101
196
根据以上数据,绘制了散点图.
(1)根据散点图判断,在推广期内, y=a+bx 与 y=c?dx ( c,?d 均为大于零的常数),哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表1中的数据,建立y与x的回归方程,并预测活动推出第8天使用扫码支付的人次;
(3)推广期结束后,车队对乘客的支付方式进行统计,结果如下表:
支付方式
现金
乘车卡
扫码
比例
10%
60%
30%
西安公交六公司车队为缓解周边居民出行压力,以90万元的单价购进了一批新车,根据以往的经验可知,每辆车每个月的运营成本约为0.66万元.已知该线路公交车票价为2元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受8折优惠,扫码支付的乘客随机优惠,根据统计结果得知,使用扫码支付的乘客中有 16 的概率享受7折优惠,有 13 的概率享受8折优惠,有 12 的概率享受9折优惠.预计该车队每辆车每个月有2万人次乘车,根据所给数据以事件发生的频率作为相应事件发生的概率,在不考虑其它因素的条件下,按照上述收费标准,请你估计这批车辆需要几年(结果取整数年)才能盈利?
参考数据:
y
v
i=17xiyi
i=17xivi
100.54
62.14
1.54
2535
50.12
3.47
其中其中 vi=lgyi , v=17i=17vi ,
参考公式:对于一组数据 (u1,?v1) , (u2,?v2) ,…, (un,?vn) ,其回归直线 v=α+βu 的斜率和截距的最小二乘估计公式分别为: β=i=1nuivi?nu?vi=1nui2?nu2 , α=v?βu .
13.某公司为一所山区小学安装了价值2万元的一台饮用水净化设备,每年都要为这台设备支出保养维修费用,我们称之为设备年度保养维修费.下表是该公司第 x 年为这台设备支出的年度保养维修费 y (单位:千元)的部分数据:
x
2
3
4
5
6
y
2.1
3.4
5.9
6.6
7.0
画出散点图如下:
通过计算得 y 与 x 的相关系数 r≈0.96 .由散点图和相关系数 r 的值可知, y 与 x 的线性相关程度很高.
附: b=i=1n(xi?x)(yi?y)i=1n(xi?x)2 , a=y?bx .
(1)建立 y 关于 x 的线性回归方程 y=bx+a ;
(2)若设备年度保养维修费不超过1.93万元就称该设备当年状态正常,根据(1)得到的线性回归方程,估计这台设备有多少年状态正常?
14.某种机械设备随着使用年限的增加,它的使用功能逐渐减退,使用价值逐年减少,通常把它使用价值逐年减少的“量”换算成费用,称之为“失效费”.某种机械设备的使用年限 x (单位:年)与失效费 y (单位:万元)的统计数据如下表所示:
使用年限 x (单位:年)
1
2
3
4
5
6
7
失效费 y (单位:万元)
2.90
3.30
3.60
4.40
4.80
5.20
5.90
(Ⅰ)由上表数据可知,可用线性回归模型拟合 y 与 x 的关系.请用相关系数加以说明;(精确到0.01)
(Ⅱ)求出 y 关于 x 的线性回归方程,并估算该种机械设备使用10年的失效费.
参考公式:相关系数 r=i=1n(xi?x)(yi?y)i=1n(xi?x)2i=1n(yi?y)2 .
线性回归方程 y=bx+a 中斜率和截距最小二乘估计计算公式: b=i=1n(xi?x)(yi?y)i=1n(xi?x)2 , a=y?bx .
参考数据: i=17(xi?x)(yi?y)=14.00 , i=17(yi?y)2=7.08 , 198.24≈14.10 .
---------------------------------------------------------------参考答案------------------------------------------------------------
1.【答案】 C 2.【答案】 D 3.【答案】 B 4.【答案】 B 5.【答案】 D 6.【答案】 C 7.【答案】 B 8.【答案】 B 9.【答案】 D 10.【答案】 59
11.【答案】 5
12.【答案】 (1)根据散点图判断,在推广期内, y=c?dx ( c,?d 均为大于零的常数),适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型;
(2)根据(1)的判断结果 y=c?dx ,两边取对数得: lgy=lgc+lgd?x ,
其中 vi=lgyi , v=17i=17vi=1.54 , i=17xivi=50.12 , x=4 , i=17xi2=140 ,
∴β=lgd=i=17xivi?nx?vi=1nxi2?nx2=0.25 , α=lgc=v?βx=0.54 ,
∴lgy=0.54+0.25x , ∴y=100.54+0.25?x=3.47×100.25x .
当 x=8 时, y=100.54+0.25?8=3.47×102=347 ,
∴活动推出第8天使用扫码支付的人次为3470人;
(3)设一名乘客一次乘车的费用为 ξ 元,
由题意知: ξ 所有可能取值为:1.4,1.6,1.8,2,
∴P(ξ=1.4)=0.3×16=0.05 , P(ξ=1.6)=0.6+0.3×13=0.7 , P(ξ=1.8)=0.3×12=0.15 , P(ξ=2)=0.1 ,
∴E(ξ)=1.4×0.05+1.6×0.7+1.8×0.15+2×0.1=1.66 ,
假设这批车需要 n(n∈N?) 年才能开始盈利,则 1.66×2×12×n≥90+0.66×12×n ,
解得: n≥2.82 ,∴需要3年才能盈利.
13.【答案】 (1)解: x=15×(2+3+4+5+6)=4 ,
y=15×(2.1+3.4+5.9+6.6+7)=5 .
b=i=15(xi?x)(yi?y)i=15(xi?x)2=1310=1.3 .
∴a=y?bx=5?1.3×4=?0.2 .
∴ 线性回归方程为 y=1.3x?0.2 .
(2)解:设这台设备有 x 年状态正常,由已知得 y≤19.3 ,即 1.3x?0.2≤19.3 .
解 1.3x?0.2≤19.3 得 x≤15 .
∴ 估计该设备有 15 年状态正常
14.【答案】 解:(Ⅰ)由题意,知 x=1+2+3+4+5+6+77=4 , y=2.90+3.30+3.60+4.40+4.80+5.20+5.907=4.30 ,
i=17(xi?x)2=(1?4)2+(2?4)2+(3?4)2+(4?4)2+(5?4)2+(6?4)2+(7?4)2=28 .
∴结合参考数据知: r=14.0028×7.08=14.00198.24≈14.0014.10≈0.99 .
因为 y 与 x 的相关系数近似为0.99,所以 y 与 x 的线性相关程度相当大,从而可以用线性回归模型拟合 y 与 x 的关系.
(Ⅱ)∵ b=i=17(xi?x)(yi?y)i=17(xi?x)2=1428=0.5 ,
∴ a=y?bx=4.3?0.5×4=2.3 .
∴ y 关于 x 的线性回归方程为 y=0.5x+2.3 ,将 x=10 代入线性回归方程,得 y=0.5×10+2.3=7.3 .
∴估算该种机械设备使用10年的失效费为7.3万元.
