湘教版七年级数学下册第4章相交线与平行线单元测试题(word版含答案)
文档属性
| 名称 | 湘教版七年级数学下册第4章相交线与平行线单元测试题(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-03 00:00:00 | ||
图片预览

文档简介
第4章 相交线与平行线测试题
一、选择题(本大题共9小题,每小题3分,共27分)
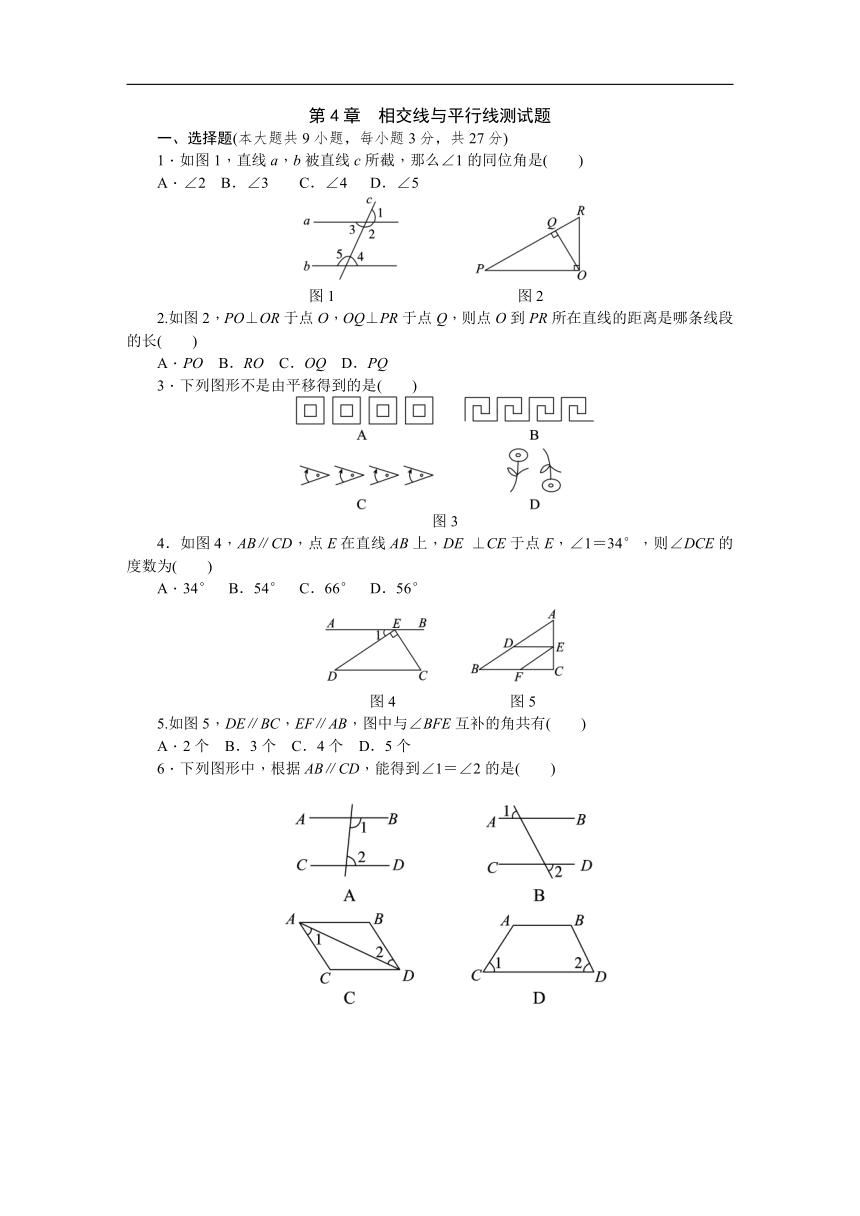
1.如图1,直线a,b被直线c所截,那么∠1的同位角是( )
A.∠2
B.∠3
C.∠4
D.∠5
图1
图2
2.如图2,PO⊥OR于点O,OQ⊥PR于点Q,则点O到PR所在直线的距离是哪条线段的长( )
A.PO
B.RO
C.OQ
D.PQ
3.下列图形不是由平移得到的是( )
图3
4.如图4,AB∥CD,点E在直线AB上,DE
⊥CE于点E,∠1=34°,则∠DCE的度数为( )
A.34°
B.54°
C.66°
D.56°
图4
图5
5.如图5,DE∥BC,EF∥AB,图中与∠BFE互补的角共有( )
A.2个
B.3个
C.4个
D.5个
6.下列图形中,根据AB∥CD,能得到∠1=∠2的是( )
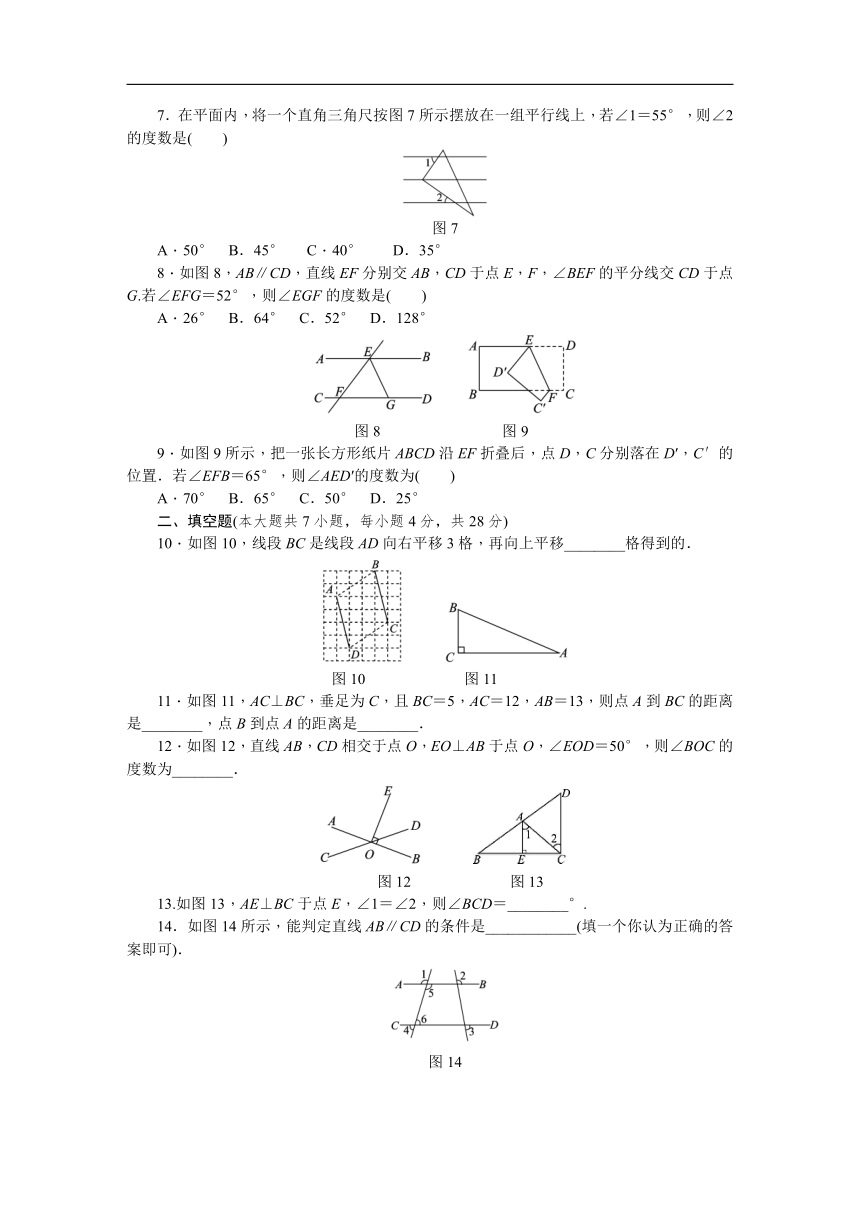
7.在平面内,将一个直角三角尺按图7所示摆放在一组平行线上,若∠1=55°,则∠2的度数是( )
图7
A.50°
B.45°
C.40°
D.35°
8.如图8,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线交CD于点G.若∠EFG=52°,则∠EGF的度数是( )
A.26°
B.64°
C.52°
D.128°
图8
图9
9.如图9所示,把一张长方形纸片ABCD沿EF折叠后,点D,C分别落在D′,C′的位置.若∠EFB=65°,则∠AED′的度数为( )
A.70°
B.65°
C.50°
D.25°
二、填空题(本大题共7小题,每小题4分,共28分)
10.如图10,线段BC是线段AD向右平移3格,再向上平移________格得到的.
图10
图11
11.如图11,AC⊥BC,垂足为C,且BC=5,AC=12,AB=13,则点A到BC的距离是________,点B到点A的距离是________.
12.如图12,直线AB,CD相交于点O,EO⊥AB于点O,∠EOD=50°,则∠BOC的度数为________.
图12
图13
13.如图13,AE⊥BC于点E,∠1=∠2,则∠BCD=________°.
14.如图14所示,能判定直线AB∥CD的条件是____________(填一个你认为正确的答案即可).
图14
15.如图15,两幢互相平行的大楼顶部各有一个射灯,当光柱相交时,∠1+∠2+∠3=________°.
图15
图16
16.如图16,直线l1∥l2,AB⊥CD,∠1=34°,那么∠2的度数是________.
三、解答题(本大题共4小题,共45分)
17.(8分)如图17,已知AB∥DC,∠A=∠C,试说明:∠B=∠D.
图17
18.(10分)如图18,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.
(1)若∠BOD=70°,求∠AOM和∠CON的度数;
(2)若∠BON=50°,求∠AOM和∠CON的度数.
图18
19.(12分)如图19,∠ABD和∠BDC的平分线交于点E,BE的延长线交CD于点F,且∠1+∠2=90°.猜想∠2与∠3的关系,并说明理由.
图19
20.(15分)如图20①所示,已知BC∥OA,∠B=∠A=100°,试解答下列问题:
(1)试说明:OB∥AC.
(2)如图②,若点E,F在BC上,且∠FOC=∠AOC,OE平分∠BOF,试求∠EOC的度数.
(3)在(2)的条件下,若左右平行移动AC,如图③,则∠OCB∶∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.
图20
参考答案
1.[解析]
C 由同位角的定义可知,∠1的同位角是∠4.
2.[答案]
C
3.[答案]
D
4.[答案]
D
5.[答案]
C
6.[答案]
B
7.[答案]
D
8.[答案]
B
9.[解析]
C 在长方形ABCD中,AD∥BC,所以∠DEF=∠EFB=65°(两直线平行,内错角相等).由折叠过程可知∠DEF=∠D′EF=65°,所以∠AED′=180°-(∠DEF+∠D′EF)=180°-(65°+65°)=50°.故选C.
10.[答案]
2
11.[答案]
12 13
12.[答案]
140°
[解析]
因为直线AB,CD相交于点O,EO⊥AB于点O,所以∠EOB=90°.
因为∠EOD=50°,所以∠BOD=40°,则∠BOC的度数为180°-40°=140°.
13.[答案]
90
14.[答案]
答案不唯一,如∠5+∠6=180°
15.[答案]
360
16.[答案]
56°
17.解:因为AB∥DC(已知),
所以∠B+∠C=180°(两直线平行,同旁内角互补).
又因为∠A=∠C(已知),
所以∠B+∠A=180°(等量代换),
所以AD∥BC(同旁内角互补,两直线平行),
所以∠C+∠D=180°(两直线平行,同旁内角互补),
所以∠B=∠D(等量代换).
18.解:(1)因为∠BOD=70°,所以∠AOC=70°.
因为射线OM平分∠AOC,所以∠AOM=∠MOC=35°.因为ON⊥OM,所以∠CON=90°-35°=55°.
(2)因为ON⊥OM,∠BON=50°,
所以∠AOM=180°-90°-50°=40°.
因为射线OM平分∠AOC,所以∠AOM=∠MOC=40°,
所以∠CON=90°-40°=50°.
19.解:∠2+∠3=90°.理由如下:
因为∠ABD和∠BDC的平分线交于点E,
所以∠ABD=2∠1,∠BDC=2∠2.
因为∠1+∠2=90°,
所以∠ABF+∠2=90°,∠ABD+∠BDC=2×90°=180°,
所以AB∥CD,
所以∠3=∠ABF,
所以∠2+∠3=90°.
20.解:(1)因为BC∥OA,
所以∠B+∠O=180°.
因为∠B=∠A,
所以∠A+∠O=180°,
所以OB∥AC.
(2)因为∠B+∠BOA=180°,∠B=100°,
所以∠BOA=80°.
因为OE平分∠BOF,
所以∠BOE=∠EOF.
又因为∠FOC=∠AOC,
所以∠EOC=∠EOF+∠FOC=(∠BOF+∠FOA)=∠BOA=40°.
(3)∠OCB∶∠OFB的值不发生变化.
因为BC∥OA,
所以∠FCO=∠AOC.
又因为∠FOC=∠AOC,
所以∠FOC=∠FCO.
因为∠FOC+∠FCO+∠OFC=180°,
∠OFB+∠OFC=180°,
所以∠OFB=∠FOC+∠FCO=2∠OCB,
所以∠OCB∶∠OFB=1∶2.
一、选择题(本大题共9小题,每小题3分,共27分)
1.如图1,直线a,b被直线c所截,那么∠1的同位角是( )
A.∠2
B.∠3
C.∠4
D.∠5
图1
图2
2.如图2,PO⊥OR于点O,OQ⊥PR于点Q,则点O到PR所在直线的距离是哪条线段的长( )
A.PO
B.RO
C.OQ
D.PQ
3.下列图形不是由平移得到的是( )
图3
4.如图4,AB∥CD,点E在直线AB上,DE
⊥CE于点E,∠1=34°,则∠DCE的度数为( )
A.34°
B.54°
C.66°
D.56°
图4
图5
5.如图5,DE∥BC,EF∥AB,图中与∠BFE互补的角共有( )
A.2个
B.3个
C.4个
D.5个
6.下列图形中,根据AB∥CD,能得到∠1=∠2的是( )
7.在平面内,将一个直角三角尺按图7所示摆放在一组平行线上,若∠1=55°,则∠2的度数是( )
图7
A.50°
B.45°
C.40°
D.35°
8.如图8,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线交CD于点G.若∠EFG=52°,则∠EGF的度数是( )
A.26°
B.64°
C.52°
D.128°
图8
图9
9.如图9所示,把一张长方形纸片ABCD沿EF折叠后,点D,C分别落在D′,C′的位置.若∠EFB=65°,则∠AED′的度数为( )
A.70°
B.65°
C.50°
D.25°
二、填空题(本大题共7小题,每小题4分,共28分)
10.如图10,线段BC是线段AD向右平移3格,再向上平移________格得到的.
图10
图11
11.如图11,AC⊥BC,垂足为C,且BC=5,AC=12,AB=13,则点A到BC的距离是________,点B到点A的距离是________.
12.如图12,直线AB,CD相交于点O,EO⊥AB于点O,∠EOD=50°,则∠BOC的度数为________.
图12
图13
13.如图13,AE⊥BC于点E,∠1=∠2,则∠BCD=________°.
14.如图14所示,能判定直线AB∥CD的条件是____________(填一个你认为正确的答案即可).
图14
15.如图15,两幢互相平行的大楼顶部各有一个射灯,当光柱相交时,∠1+∠2+∠3=________°.
图15
图16
16.如图16,直线l1∥l2,AB⊥CD,∠1=34°,那么∠2的度数是________.
三、解答题(本大题共4小题,共45分)
17.(8分)如图17,已知AB∥DC,∠A=∠C,试说明:∠B=∠D.
图17
18.(10分)如图18,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.
(1)若∠BOD=70°,求∠AOM和∠CON的度数;
(2)若∠BON=50°,求∠AOM和∠CON的度数.
图18
19.(12分)如图19,∠ABD和∠BDC的平分线交于点E,BE的延长线交CD于点F,且∠1+∠2=90°.猜想∠2与∠3的关系,并说明理由.
图19
20.(15分)如图20①所示,已知BC∥OA,∠B=∠A=100°,试解答下列问题:
(1)试说明:OB∥AC.
(2)如图②,若点E,F在BC上,且∠FOC=∠AOC,OE平分∠BOF,试求∠EOC的度数.
(3)在(2)的条件下,若左右平行移动AC,如图③,则∠OCB∶∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.
图20
参考答案
1.[解析]
C 由同位角的定义可知,∠1的同位角是∠4.
2.[答案]
C
3.[答案]
D
4.[答案]
D
5.[答案]
C
6.[答案]
B
7.[答案]
D
8.[答案]
B
9.[解析]
C 在长方形ABCD中,AD∥BC,所以∠DEF=∠EFB=65°(两直线平行,内错角相等).由折叠过程可知∠DEF=∠D′EF=65°,所以∠AED′=180°-(∠DEF+∠D′EF)=180°-(65°+65°)=50°.故选C.
10.[答案]
2
11.[答案]
12 13
12.[答案]
140°
[解析]
因为直线AB,CD相交于点O,EO⊥AB于点O,所以∠EOB=90°.
因为∠EOD=50°,所以∠BOD=40°,则∠BOC的度数为180°-40°=140°.
13.[答案]
90
14.[答案]
答案不唯一,如∠5+∠6=180°
15.[答案]
360
16.[答案]
56°
17.解:因为AB∥DC(已知),
所以∠B+∠C=180°(两直线平行,同旁内角互补).
又因为∠A=∠C(已知),
所以∠B+∠A=180°(等量代换),
所以AD∥BC(同旁内角互补,两直线平行),
所以∠C+∠D=180°(两直线平行,同旁内角互补),
所以∠B=∠D(等量代换).
18.解:(1)因为∠BOD=70°,所以∠AOC=70°.
因为射线OM平分∠AOC,所以∠AOM=∠MOC=35°.因为ON⊥OM,所以∠CON=90°-35°=55°.
(2)因为ON⊥OM,∠BON=50°,
所以∠AOM=180°-90°-50°=40°.
因为射线OM平分∠AOC,所以∠AOM=∠MOC=40°,
所以∠CON=90°-40°=50°.
19.解:∠2+∠3=90°.理由如下:
因为∠ABD和∠BDC的平分线交于点E,
所以∠ABD=2∠1,∠BDC=2∠2.
因为∠1+∠2=90°,
所以∠ABF+∠2=90°,∠ABD+∠BDC=2×90°=180°,
所以AB∥CD,
所以∠3=∠ABF,
所以∠2+∠3=90°.
20.解:(1)因为BC∥OA,
所以∠B+∠O=180°.
因为∠B=∠A,
所以∠A+∠O=180°,
所以OB∥AC.
(2)因为∠B+∠BOA=180°,∠B=100°,
所以∠BOA=80°.
因为OE平分∠BOF,
所以∠BOE=∠EOF.
又因为∠FOC=∠AOC,
所以∠EOC=∠EOF+∠FOC=(∠BOF+∠FOA)=∠BOA=40°.
(3)∠OCB∶∠OFB的值不发生变化.
因为BC∥OA,
所以∠FCO=∠AOC.
又因为∠FOC=∠AOC,
所以∠FOC=∠FCO.
因为∠FOC+∠FCO+∠OFC=180°,
∠OFB+∠OFC=180°,
所以∠OFB=∠FOC+∠FCO=2∠OCB,
所以∠OCB∶∠OFB=1∶2.
