湖南师大附中高新实验中学2020-2021学年八年级下学期第一次月考数学试卷 (word版含解析)
文档属性
| 名称 | 湖南师大附中高新实验中学2020-2021学年八年级下学期第一次月考数学试卷 (word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 308.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 00:00:00 | ||
图片预览


文档简介
2020-2021学年湖南师大附中高新实验中学八年级(下)第一次月考数学试卷
一、选择题(在下列各题的四个选项中,只有一项是符合题意的.本大题共12个小题,每小题3分,共36分)
1.下列图形是轴对称图形的是( )
A.
B.
C.
D.
2.下列计算正确的是( )
A.a+2a=3a
B.a2?a3=a6
C.a3÷a=3
D.3x﹣2x=1
3.2020年,新冠肺炎在全球肆虐,截止9月下旬,将38703120用科学记数表示为( )
A.38.70312×106
B.3.870312×107
C.3.870312×106
D.3.870312×108
4.在平行四边形ABCD中,∠A:∠B:∠C:∠D的值可以是( )
A.1:2:3:4
B.1:2:2:1
C.1:1:2:2
D.2:1:2:1
5.下列性质中菱形不一定具有的性质是( )
A.四条边都相等
B.对角线垂直且平分
C.对角线相等
D.对角线平分一组对角
6.下列数据能作为直角三角形三边长的是( )
A.6,7,8
B.1,,2
C.5,12,14
D.7,24,26
7.下列说法中不正确的是( )
A.对角线垂直的平行四边形是菱形
B.四边相等的四边形是菱形
C.菱形的对角线互相垂直且相等
D.菱形的邻边相等
8.如图,长方形OABC的边OA长为2,AB长为1,以原点O为圆心,对角线OB的长为半径画弧,则这个点表示的实数是( )
A.2.5
B.
C.
D.3
9.如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,那么△DEF的周长是( )
A.5
B.10
C.15
D.20
10.在四边形ABCD中,对角线AC,BD相交于点O,OB=OD.若要使四边形ABCD为菱形,则可以添加的条件是( )
A.∠AOB=60°
B.AC⊥BD
C.AC=BD
D.AB⊥BC
11.如图,在平行四边形ABCD中,DE平分∠ADC,BE=2,则平行四边形ABCD的周长是( )
A.16
B.18
C.20
D.24
12.如图,已知△ABC中,AB=AC,AE是∠BAC的外角平分线,ED∥AB交AC于点G
①AD⊥BC;②AE∥BC;③AE=AG2+AE2=4AG2.
其中正确结论的个数是( )
A.1
B.2
C.3
D.4
二、填空题(本大题共4个小题,每小题3分,共12分)
13.一个n边形的各内角都等于120°,则边数n是
.
14.若菱形的两条对角线长分别是6和8,则此菱形的周长是
,面积是
.
15.已知直角三角形的长为3cm、5cm,则第三边长为
cm.
16.如图,在矩形ABCD中,AB=10,动点P满足S△PAB=S矩形ABCD,则点P到A,B两点距离之和PA+PB的最小值为
.
三、解答题(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题6分,第22、23题每小题6分,第24、25题每小题6分,共72分,解答应写出必要的文字说明、证明过程或演算步骤)
17.(6分)(1)分解因式:3x2y﹣6xy+3y;
(2)化简:.
18.(6分)计算:
(1);
(2).
19.(6分)解下列分式方程:
(1);
(2).
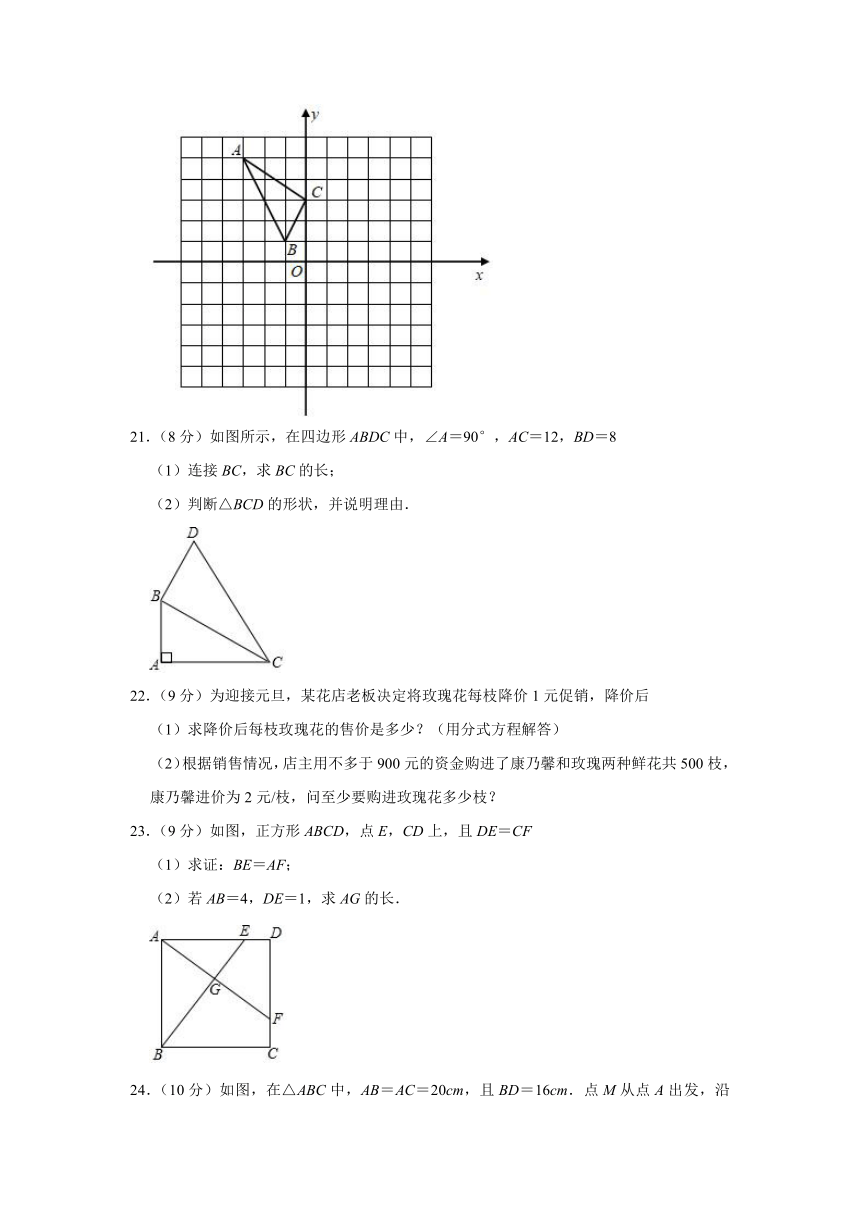
20.(8分)在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形),C的坐标分别为A(﹣3,5),C(0,3).
(1)请在如图所示的网格内作出ABC关于y轴对称的△A1B1C1.
(2)写出点B1的坐标并求出△A1B1C1的面积.
21.(8分)如图所示,在四边形ABDC中,∠A=90°,AC=12,BD=8
(1)连接BC,求BC的长;
(2)判断△BCD的形状,并说明理由.
22.(9分)为迎接元旦,某花店老板决定将玫瑰花每枝降价1元促销,降价后
(1)求降价后每枝玫瑰花的售价是多少?(用分式方程解答)
(2)根据销售情况,店主用不多于900元的资金购进了康乃馨和玫瑰两种鲜花共500枝,康乃馨进价为2元/枝,问至少要购进玫瑰花多少枝?
23.(9分)如图,正方形ABCD,点E,CD上,且DE=CF
(1)求证:BE=AF;
(2)若AB=4,DE=1,求AG的长.
24.(10分)如图,在△ABC中,AB=AC=20cm,且BD=16cm.点M从点A出发,沿AC方向匀速运动;同时点P由B点出发,沿BA方向匀速运动,过点P的直线PQ∥AC,交BC于点Q,设运动时间为t(s)(0<t<5),解答下列问题:
(1)线段AD=
cm;
(2)求证:PB=PQ;
(3)当t为何值时,以P、Q、D、M为顶点的四边形是平行四边形?
25.(10分)如图,在?ABCD中,∠BAD的平分线交BC于点E,以EC、CF为邻边作?ECFG.
(1)证明?ECFG是菱形;
(2)若∠ABC=120°,连接BD、CG,求∠BDG的度数;
(3)若∠ABC=90°,AB=6,AD=8,求DM的长.
2020-2021学年湖南师大附中高新实验中学八年级(下)第一次月考数学试卷
参考答案与试题解析
一、选择题(在下列各题的四个选项中,只有一项是符合题意的.本大题共12个小题,每小题3分,共36分)
1.下列图形是轴对称图形的是( )
A.
B.
C.
D.
【分析】根据轴对称图形的概念对各选项分析判断即可得解.
【解答】解:A、不是轴对称图形;
B、是轴对称图形;
C、不是轴对称图形;
D、不是轴对称图形.
故选:B.
2.下列计算正确的是( )
A.a+2a=3a
B.a2?a3=a6
C.a3÷a=3
D.3x﹣2x=1
【分析】分别根据合并同类项法则,同底数幂的乘法法则,同底数幂的除法法则逐一判断即可.
【解答】解:A、a+2a=3a;
B、a7?a3=a5,故本选项不符合题意;
C、a4÷a=a2,故本选项不符合题意;
D、3x﹣4x=x.
故选:A.
3.2020年,新冠肺炎在全球肆虐,截止9月下旬,将38703120用科学记数表示为( )
A.38.70312×106
B.3.870312×107
C.3.870312×106
D.3.870312×108
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:38703120=3.870312×107,
故选:B.
4.在平行四边形ABCD中,∠A:∠B:∠C:∠D的值可以是( )
A.1:2:3:4
B.1:2:2:1
C.1:1:2:2
D.2:1:2:1
【分析】根据平行四边形的对角相等,容易得出结论.
【解答】解:∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D,
∴D正确,
故选:D.
5.下列性质中菱形不一定具有的性质是( )
A.四条边都相等
B.对角线垂直且平分
C.对角线相等
D.对角线平分一组对角
【分析】由菱形的性质依次判断可求解.
【解答】解:菱形的性质有四边都相等,对角线互相垂直平分,
故选:C.
6.下列数据能作为直角三角形三边长的是( )
A.6,7,8
B.1,,2
C.5,12,14
D.7,24,26
【分析】如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.根据勾股定理的逆定理即可判断.
【解答】解:A、62+62≠86,根据勾股定理的逆定理可知三角形不是直角三角形,故不合题意;
B、12+()2=22,根据勾股定理的逆定理可知三角形是直角三角形,故符合题意;
C、122+53≠142,根据勾股定理的逆定理可知三角形不是直角三角形,故不合题意;
D、77+242≠262,根据勾股定理的逆定理可知三角形不是直角三角形,故不合题意;
故选:B.
7.下列说法中不正确的是( )
A.对角线垂直的平行四边形是菱形
B.四边相等的四边形是菱形
C.菱形的对角线互相垂直且相等
D.菱形的邻边相等
【分析】由菱形的判定与性质即可得出A、B、D正确,C不正确.
【解答】解:A.对角线垂直的平行四边形是菱形;
B.四边相等的四边形是菱形;
C.菱形的对角线互相垂直且相等;
D.菱形的邻边相等;
故选:C.
8.如图,长方形OABC的边OA长为2,AB长为1,以原点O为圆心,对角线OB的长为半径画弧,则这个点表示的实数是( )
A.2.5
B.
C.
D.3
【分析】本题利用实数与数轴的关系及直角三角形三边的关系(勾股定理)解答即可.
【解答】解:由勾股定理可知,
∵OB==,
∴这个点表示的实数是.
故选:C.
9.如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,那么△DEF的周长是( )
A.5
B.10
C.15
D.20
【分析】利用三角形的中位线定理可以得到:DE=AC,EF=BC,DF=AB,则△DEF的周长是△ABC的周长的一半,据此即可求解.
【解答】解:∵D、E分别是△ABC的边BC,
∴DE=AC,
同理
EF=BCAB,
∴C△DEF=DE+EF+DF=(AC+BC+AB)=.
故选:B.
10.在四边形ABCD中,对角线AC,BD相交于点O,OB=OD.若要使四边形ABCD为菱形,则可以添加的条件是( )
A.∠AOB=60°
B.AC⊥BD
C.AC=BD
D.AB⊥BC
【分析】由条件OA=OC,OB=OD根据对角线互相平分的四边形是平行四边形可得四边形ABCD为平行四边形,再由矩形和菱形的判定定理即可得出结论.
【解答】解:∵OA=OC,OB=OD,
∴四边形ABCD为平行四边形,
A、∵∠AOB=60°,
∴不能得出四边形ABCD是菱形;选项A不符合题意;
B、∵AC⊥BD,
∴四边形ABCD是菱形,故选项B符合题意;
C、∵AC=BD,
∴四边形ABCD是矩形,故选项C不符合题意;
D、∵AB⊥BC,
∴四边形ABCD是矩形,故选项D不符合题意;
故选:B.
11.如图,在平行四边形ABCD中,DE平分∠ADC,BE=2,则平行四边形ABCD的周长是( )
A.16
B.18
C.20
D.24
【分析】根据角平分线的定义以及两直线平行,内错角相等求出∠CDE=∠CED,再根据等角对等边的性质可得CE=CD,然后利用平行四边形对边相等求出CD、BC的长度,再求出?ABCD的周长.
【解答】解:∵DE平分∠ADC,
∴∠ADE=∠CDE,
∵?ABCD中,AD∥BC,
∴∠ADE=∠CED,
∴∠CDE=∠CED,
∴CE=CD,
∵在?ABCD中,AD=6,
∴AD=BC=6,
∴CE=BC﹣BE=7﹣2=4,
∴CD=AB=7,
∴?ABCD的周长=6+6+4+4=20.
故选:C.
12.如图,已知△ABC中,AB=AC,AE是∠BAC的外角平分线,ED∥AB交AC于点G
①AD⊥BC;②AE∥BC;③AE=AG2+AE2=4AG2.
其中正确结论的个数是( )
A.1
B.2
C.3
D.4
【分析】连接EC,根据等腰三角形的性质得出AD⊥BC,即可判断①;求出∠FAE=∠B,再根据平行线的性质得出AE∥BC,即可判断②;求出四边形ABDE是平行四边形,根据平行四边形的性质得出AE=BD,求出AE=CD,根据矩形的判定推出四边形ADCE是矩形,根据矩形的性质得出AC=DE,AG=CG,DG=EG,求出DG=AG=CG=EG,根据勾股定理判断④即可;根据AE=BD=BC和AG=AC判断③即可.
【解答】解:连接EC,
∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,故①正确;
∵AB=AC,
∴∠B=∠ACB,
∵AE平分∠FAC,
∴∠FAC=2∠FAE,
∵∠FAC=∠B+∠ACB,
∴∠FAE=∠B,
∴AE∥BC,故②正确;
∵AE∥BC,DE∥AB,
∴四边形ABDE是平行四边形,
∴AE=BD,
∵AB=AC,AD⊥BC,
∴CD=BD,
∴AE=CD,
∵AE∥BC,∠ADC=90°,
∴四边形ADCE是矩形,
∴AC=DE,AG=CG,
∴DG=AG=CG=EG,
在Rt△AED中,AD2+AE3=DE2=AC2=(6AG)2=4AG2,故④正确;
∵AE=BD=BCAC,
∴AG=AE错误(已知没有条件AC=BC),故③错误;
即正确的个数是3个,
故选:C.
二、填空题(本大题共4个小题,每小题3分,共12分)
13.一个n边形的各内角都等于120°,则边数n是 6 .
【分析】首先求出外角度数,再用360°除以外角度数可得答案.
【解答】解:∵n边形的各内角都等于120°,
∴每一个外角都等于180°﹣120°=60°,
∴边数n=360°÷60°=6.
故答案为:6.
14.若菱形的两条对角线长分别是6和8,则此菱形的周长是 20 ,面积是 24 .
【分析】首先根据题意画出图形,然后由菱形的两条对角线长分别是6和8,可求得OA=4,OB=3,再由勾股定理求得边长,继而求得此菱形的周长与面积.
【解答】解:如图,菱形ABCD中,BD=6,
∴OA=AC=4BD=3,
∴AB==5,
∴此菱形的周长是:5×8=20,面积是:.
故答案为:20,24.
15.已知直角三角形的长为3cm、5cm,则第三边长为 或4 cm.
【分析】分类讨论:①当5为直角边时,②当5为斜边时,根据勾股定理依次求出答案即可.
【解答】解:①当5是直角边时,斜边==;
②当7为斜边时,此时第三边=.
综上可得,第三边的长度为.
故答案为:或4.
16.如图,在矩形ABCD中,AB=10,动点P满足S△PAB=S矩形ABCD,则点P到A,B两点距离之和PA+PB的最小值为 2 .
【分析】首先由S△PAB=S矩形ABCD,得出动点P在与AB平行且与AB的距离是4的直线l上,作A关于直线l的对称点E,连接AE,连接BE,则BE的长就是所求的最短距离.然后在直角三角形ABE中,由勾股定理求得BE的值,即PA+PB的最小值.
【解答】解:设△ABP中AB边上的高是h.
∵S△PAB=S矩形ABCD,
∴AB?h=,
∴h=AD=7,
∴动点P在与AB平行且与AB的距离是2的直线l上,如图,连接AE,则BE的长就是所求的最短距离.
在Rt△ABE中,∵AB=10,
∴BE===7,
即PA+PB的最小值为2.
故答案为:2.
三、解答题(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题6分,第22、23题每小题6分,第24、25题每小题6分,共72分,解答应写出必要的文字说明、证明过程或演算步骤)
17.(6分)(1)分解因式:3x2y﹣6xy+3y;
(2)化简:.
【分析】(1)先题公因式,再用公式分解.
(2)先算括号内,再算括号外.
【解答】解:(1)原式=3y(x2﹣8x+1)
=3y(x﹣5)2.
(2)原式=(+)×
=×
=.
18.(6分)计算:
(1);
(2).
【分析】(1)先根据零指数幂,二次根式的性质,有理数的乘方,二次根式的乘法进行计算,再求出答案即可;
(2)先根据二次根式的乘法和除法进行计算,再求出答案即可.
【解答】解:(1)原式=1+2+9﹣2
=10;
(2)原式=3﹣1+
=2+
=7+2.
19.(6分)解下列分式方程:
(1);
(2).
【分析】将分式方程化为整式方程,解整式方程然后检验即可.
【解答】解:(1)方程两边都乘以5x(x+2)得:8(x+2)=5x,
解得:x=6,
经检验,x=3是原方程的根.
(2)方程两边都乘以(x﹣1)得8x﹣1﹣(x﹣1)=2,
解得:x=,
经检验,x=.
20.(8分)在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形),C的坐标分别为A(﹣3,5),C(0,3).
(1)请在如图所示的网格内作出ABC关于y轴对称的△A1B1C1.
(2)写出点B1的坐标并求出△A1B1C1的面积.
【分析】(1)分别作出A,B,C的对应点A1,B1,C1即可.
(2)利用分割法求解即可.
【解答】解:(1)如图,称的△A1B1C2即为所求作.
(2)点B1的坐标(1,3)1B1C4的面积=3×4﹣×1×7﹣×2×3=4.
21.(8分)如图所示,在四边形ABDC中,∠A=90°,AC=12,BD=8
(1)连接BC,求BC的长;
(2)判断△BCD的形状,并说明理由.
【分析】(1)直接利用勾股定理得出BC的长;
(2)直接利用勾股定理逆定理进而分析得出答案.
【解答】解:(1)∵∠A=90°,
∴BC===15;
(2)△BCD是直角三角形,
理由:∵BC2=155=225,
BD2=85=64,
CD2=172=289,
∴BC8+BD2=CD2=289,
∴△BCD是直角三角形.
22.(9分)为迎接元旦,某花店老板决定将玫瑰花每枝降价1元促销,降价后
(1)求降价后每枝玫瑰花的售价是多少?(用分式方程解答)
(2)根据销售情况,店主用不多于900元的资金购进了康乃馨和玫瑰两种鲜花共500枝,康乃馨进价为2元/枝,问至少要购进玫瑰花多少枝?
【分析】(1)可设降价后每枝玫瑰的售价是x元,根据等量关系:降价后30元可购买玫瑰的数量=原来购买玫瑰数量的1.5倍,列出方程求解即可;
(2)可设购进玫瑰y枝,根据不等量关系:购进康乃馨的钱数+购进玫瑰的钱数≤900元,列出不等式求解即可.
【解答】解:(1)设降价后每枝玫瑰的售价是x元,
由题意可得:×1.8,
解得:x=2.
经检验,x=2是原方程的解.
答:降价后每枝玫瑰的售价是4元.
(2)设购进玫瑰y枝,依题意有
2(500﹣y)+1.5y≤900,
解得:y≥200.
答:至少购进玫瑰200枝.
23.(9分)如图,正方形ABCD,点E,CD上,且DE=CF
(1)求证:BE=AF;
(2)若AB=4,DE=1,求AG的长.
【分析】(1)由正方形的性质得出∠BAE=∠ADF=90°,AB=AD=CD,得出AE=DF,由SAS证明△BAE≌△ADF,即可得出结论;
(2)由全等三角形的性质得出∠EBA=∠FAD,得出∠GAE+∠AEG=90°,因此∠AGE=90°,由勾股定理得出BE==5,在Rt△ABE中,由三角形面积即可得出结果.
【解答】(1)证明:∵四边形ABCD是正方形,
∴∠BAE=∠ADF=90°,AB=AD=CD,
∵DE=CF,
∴AE=DF,
在△BAE和△ADF中,,
∴△BAE≌△ADF(SAS),
∴BE=AF;
(2)解:由(1)得:△BAE≌△ADF,
∴∠EBA=∠FAD,
∴∠GAE+∠AEG=90°,
∴∠AGE=90°,
∵AB=4,DE=1,
∴AE=6,
∴BE===5,
在Rt△ABE中,AB×AE=,
∴AG==.
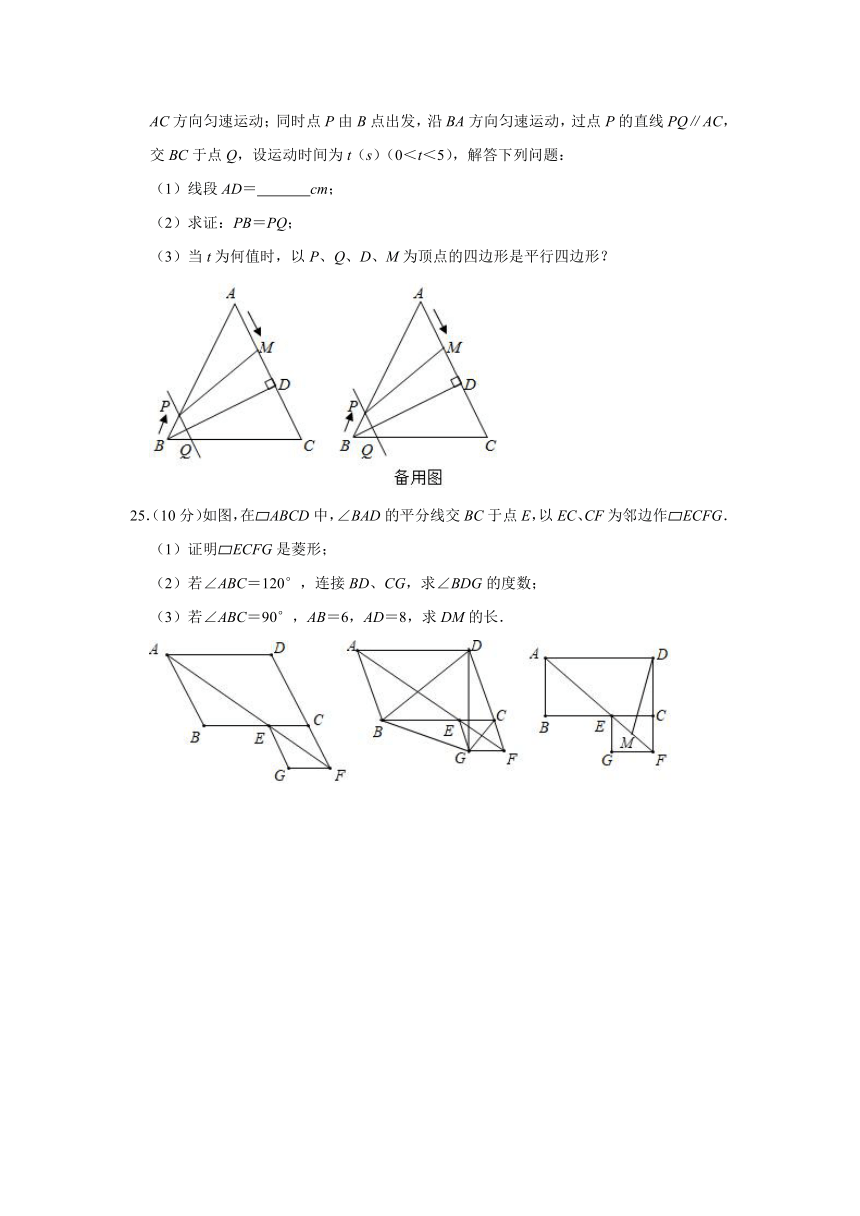
24.(10分)如图,在△ABC中,AB=AC=20cm,且BD=16cm.点M从点A出发,沿AC方向匀速运动;同时点P由B点出发,沿BA方向匀速运动,过点P的直线PQ∥AC,交BC于点Q,设运动时间为t(s)(0<t<5),解答下列问题:
(1)线段AD= 12 cm;
(2)求证:PB=PQ;
(3)当t为何值时,以P、Q、D、M为顶点的四边形是平行四边形?
【分析】(1)由勾股定理求出AD即可;
(2)由等腰三角形的性质和平行线的性质得出∠PBQ=∠PQB,再由等腰三角形的判定定理即可得出结论;
(3)分两种情况:①当点M在点D的上方时,PQ=BP=t,AM=4t,AD=12,得出MD=AD﹣AM=12﹣4t,由PQ∥MD,当PQ=MD时,四边形PQDM是平行四边形,得出方程,解方程即可;
②当点M在点D的下方时,PQ=BP=t,AM=4t,AD=12,得出MD=AM﹣AD=4t﹣12,由PQ∥MD,当PQ=MD时,四边形PQDM是平行四边形,得出方程,解方程即可.
【解答】(1)解:在Rt△ABD中,由勾股定理得:AD==,
故答案为:12;
(2)证明:如图2所示:
∵AB=AC,
∴∠ABC=∠C,即∠PBQ=∠C,
∵PQ∥AC,
∴∠PQB=∠C,
∴∠PBQ=∠PQB,
∴PB=PQ;
(3)解:分两种情况:
①当点M在点D的上方时,如图2所示:
由题意得:PQ=BP=t,AM=4t,
∴MD=AD﹣AM=12﹣6t,
∵PQ∥AC,
∴PQ∥MD,
∴当PQ=MD时,四边形PQDM是平行四边形,
即:当t=12﹣4t时,四边形PQDM是平行四边形,
解得:(s);
②当点M在点D的下方时,如图6所示:
根据题意得:PQ=BP=t,AM=4t,
∴MD=AM﹣AD=4t﹣12,
∵PQ∥AC,
∴PQ∥MD,
∴当PQ=MD时,四边形PQDM是平行四边形,
即:当t=6t﹣12时,四边形PQDM是平行四边形,
解得:t=4(s);
综上所述,当t=,以P、Q、D.
25.(10分)如图,在?ABCD中,∠BAD的平分线交BC于点E,以EC、CF为邻边作?ECFG.
(1)证明?ECFG是菱形;
(2)若∠ABC=120°,连接BD、CG,求∠BDG的度数;
(3)若∠ABC=90°,AB=6,AD=8,求DM的长.
【分析】(1)平行四边形的性质可得AD∥BC,AB∥CD,再根据平行线的性质证明∠CEF=∠CFE,根据等角对等边可得CE=CF,再有条件四边形ECFG是平行四边形,可得四边形ECFG为菱形,即可解决问题;
(2)先判断出∠BEG=120°=∠DCG,再判断出AB=BE,进而得出BE=CD,即可判断出△BEG≌△DCG(SAS),再判断出∠CGE=60°,进而得出△BDG是等边三角形,即可得出结论;
(3)首先证明四边形ECFG为正方形,再证明△BME≌△DMC可得DM=BM,∠DMC=∠BME,再根据∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°可得到△BDM是等腰直角三角形,由等腰直角三角形的性质即可得到结论.
【解答】解:(1)证明:
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG=,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△BEG≌△DCG(SAS),
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)如图4中,连接BM,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=6,AD=8,
∴BD=10,
∴DM=BD=5.
一、选择题(在下列各题的四个选项中,只有一项是符合题意的.本大题共12个小题,每小题3分,共36分)
1.下列图形是轴对称图形的是( )
A.
B.
C.
D.
2.下列计算正确的是( )
A.a+2a=3a
B.a2?a3=a6
C.a3÷a=3
D.3x﹣2x=1
3.2020年,新冠肺炎在全球肆虐,截止9月下旬,将38703120用科学记数表示为( )
A.38.70312×106
B.3.870312×107
C.3.870312×106
D.3.870312×108
4.在平行四边形ABCD中,∠A:∠B:∠C:∠D的值可以是( )
A.1:2:3:4
B.1:2:2:1
C.1:1:2:2
D.2:1:2:1
5.下列性质中菱形不一定具有的性质是( )
A.四条边都相等
B.对角线垂直且平分
C.对角线相等
D.对角线平分一组对角
6.下列数据能作为直角三角形三边长的是( )
A.6,7,8
B.1,,2
C.5,12,14
D.7,24,26
7.下列说法中不正确的是( )
A.对角线垂直的平行四边形是菱形
B.四边相等的四边形是菱形
C.菱形的对角线互相垂直且相等
D.菱形的邻边相等
8.如图,长方形OABC的边OA长为2,AB长为1,以原点O为圆心,对角线OB的长为半径画弧,则这个点表示的实数是( )
A.2.5
B.
C.
D.3
9.如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,那么△DEF的周长是( )
A.5
B.10
C.15
D.20
10.在四边形ABCD中,对角线AC,BD相交于点O,OB=OD.若要使四边形ABCD为菱形,则可以添加的条件是( )
A.∠AOB=60°
B.AC⊥BD
C.AC=BD
D.AB⊥BC
11.如图,在平行四边形ABCD中,DE平分∠ADC,BE=2,则平行四边形ABCD的周长是( )
A.16
B.18
C.20
D.24
12.如图,已知△ABC中,AB=AC,AE是∠BAC的外角平分线,ED∥AB交AC于点G
①AD⊥BC;②AE∥BC;③AE=AG2+AE2=4AG2.
其中正确结论的个数是( )
A.1
B.2
C.3
D.4
二、填空题(本大题共4个小题,每小题3分,共12分)
13.一个n边形的各内角都等于120°,则边数n是
.
14.若菱形的两条对角线长分别是6和8,则此菱形的周长是
,面积是
.
15.已知直角三角形的长为3cm、5cm,则第三边长为
cm.
16.如图,在矩形ABCD中,AB=10,动点P满足S△PAB=S矩形ABCD,则点P到A,B两点距离之和PA+PB的最小值为
.
三、解答题(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题6分,第22、23题每小题6分,第24、25题每小题6分,共72分,解答应写出必要的文字说明、证明过程或演算步骤)
17.(6分)(1)分解因式:3x2y﹣6xy+3y;
(2)化简:.
18.(6分)计算:
(1);
(2).
19.(6分)解下列分式方程:
(1);
(2).
20.(8分)在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形),C的坐标分别为A(﹣3,5),C(0,3).
(1)请在如图所示的网格内作出ABC关于y轴对称的△A1B1C1.
(2)写出点B1的坐标并求出△A1B1C1的面积.
21.(8分)如图所示,在四边形ABDC中,∠A=90°,AC=12,BD=8
(1)连接BC,求BC的长;
(2)判断△BCD的形状,并说明理由.
22.(9分)为迎接元旦,某花店老板决定将玫瑰花每枝降价1元促销,降价后
(1)求降价后每枝玫瑰花的售价是多少?(用分式方程解答)
(2)根据销售情况,店主用不多于900元的资金购进了康乃馨和玫瑰两种鲜花共500枝,康乃馨进价为2元/枝,问至少要购进玫瑰花多少枝?
23.(9分)如图,正方形ABCD,点E,CD上,且DE=CF
(1)求证:BE=AF;
(2)若AB=4,DE=1,求AG的长.
24.(10分)如图,在△ABC中,AB=AC=20cm,且BD=16cm.点M从点A出发,沿AC方向匀速运动;同时点P由B点出发,沿BA方向匀速运动,过点P的直线PQ∥AC,交BC于点Q,设运动时间为t(s)(0<t<5),解答下列问题:
(1)线段AD=
cm;
(2)求证:PB=PQ;
(3)当t为何值时,以P、Q、D、M为顶点的四边形是平行四边形?
25.(10分)如图,在?ABCD中,∠BAD的平分线交BC于点E,以EC、CF为邻边作?ECFG.
(1)证明?ECFG是菱形;
(2)若∠ABC=120°,连接BD、CG,求∠BDG的度数;
(3)若∠ABC=90°,AB=6,AD=8,求DM的长.
2020-2021学年湖南师大附中高新实验中学八年级(下)第一次月考数学试卷
参考答案与试题解析
一、选择题(在下列各题的四个选项中,只有一项是符合题意的.本大题共12个小题,每小题3分,共36分)
1.下列图形是轴对称图形的是( )
A.
B.
C.
D.
【分析】根据轴对称图形的概念对各选项分析判断即可得解.
【解答】解:A、不是轴对称图形;
B、是轴对称图形;
C、不是轴对称图形;
D、不是轴对称图形.
故选:B.
2.下列计算正确的是( )
A.a+2a=3a
B.a2?a3=a6
C.a3÷a=3
D.3x﹣2x=1
【分析】分别根据合并同类项法则,同底数幂的乘法法则,同底数幂的除法法则逐一判断即可.
【解答】解:A、a+2a=3a;
B、a7?a3=a5,故本选项不符合题意;
C、a4÷a=a2,故本选项不符合题意;
D、3x﹣4x=x.
故选:A.
3.2020年,新冠肺炎在全球肆虐,截止9月下旬,将38703120用科学记数表示为( )
A.38.70312×106
B.3.870312×107
C.3.870312×106
D.3.870312×108
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:38703120=3.870312×107,
故选:B.
4.在平行四边形ABCD中,∠A:∠B:∠C:∠D的值可以是( )
A.1:2:3:4
B.1:2:2:1
C.1:1:2:2
D.2:1:2:1
【分析】根据平行四边形的对角相等,容易得出结论.
【解答】解:∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D,
∴D正确,
故选:D.
5.下列性质中菱形不一定具有的性质是( )
A.四条边都相等
B.对角线垂直且平分
C.对角线相等
D.对角线平分一组对角
【分析】由菱形的性质依次判断可求解.
【解答】解:菱形的性质有四边都相等,对角线互相垂直平分,
故选:C.
6.下列数据能作为直角三角形三边长的是( )
A.6,7,8
B.1,,2
C.5,12,14
D.7,24,26
【分析】如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.根据勾股定理的逆定理即可判断.
【解答】解:A、62+62≠86,根据勾股定理的逆定理可知三角形不是直角三角形,故不合题意;
B、12+()2=22,根据勾股定理的逆定理可知三角形是直角三角形,故符合题意;
C、122+53≠142,根据勾股定理的逆定理可知三角形不是直角三角形,故不合题意;
D、77+242≠262,根据勾股定理的逆定理可知三角形不是直角三角形,故不合题意;
故选:B.
7.下列说法中不正确的是( )
A.对角线垂直的平行四边形是菱形
B.四边相等的四边形是菱形
C.菱形的对角线互相垂直且相等
D.菱形的邻边相等
【分析】由菱形的判定与性质即可得出A、B、D正确,C不正确.
【解答】解:A.对角线垂直的平行四边形是菱形;
B.四边相等的四边形是菱形;
C.菱形的对角线互相垂直且相等;
D.菱形的邻边相等;
故选:C.
8.如图,长方形OABC的边OA长为2,AB长为1,以原点O为圆心,对角线OB的长为半径画弧,则这个点表示的实数是( )
A.2.5
B.
C.
D.3
【分析】本题利用实数与数轴的关系及直角三角形三边的关系(勾股定理)解答即可.
【解答】解:由勾股定理可知,
∵OB==,
∴这个点表示的实数是.
故选:C.
9.如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,那么△DEF的周长是( )
A.5
B.10
C.15
D.20
【分析】利用三角形的中位线定理可以得到:DE=AC,EF=BC,DF=AB,则△DEF的周长是△ABC的周长的一半,据此即可求解.
【解答】解:∵D、E分别是△ABC的边BC,
∴DE=AC,
同理
EF=BCAB,
∴C△DEF=DE+EF+DF=(AC+BC+AB)=.
故选:B.
10.在四边形ABCD中,对角线AC,BD相交于点O,OB=OD.若要使四边形ABCD为菱形,则可以添加的条件是( )
A.∠AOB=60°
B.AC⊥BD
C.AC=BD
D.AB⊥BC
【分析】由条件OA=OC,OB=OD根据对角线互相平分的四边形是平行四边形可得四边形ABCD为平行四边形,再由矩形和菱形的判定定理即可得出结论.
【解答】解:∵OA=OC,OB=OD,
∴四边形ABCD为平行四边形,
A、∵∠AOB=60°,
∴不能得出四边形ABCD是菱形;选项A不符合题意;
B、∵AC⊥BD,
∴四边形ABCD是菱形,故选项B符合题意;
C、∵AC=BD,
∴四边形ABCD是矩形,故选项C不符合题意;
D、∵AB⊥BC,
∴四边形ABCD是矩形,故选项D不符合题意;
故选:B.
11.如图,在平行四边形ABCD中,DE平分∠ADC,BE=2,则平行四边形ABCD的周长是( )
A.16
B.18
C.20
D.24
【分析】根据角平分线的定义以及两直线平行,内错角相等求出∠CDE=∠CED,再根据等角对等边的性质可得CE=CD,然后利用平行四边形对边相等求出CD、BC的长度,再求出?ABCD的周长.
【解答】解:∵DE平分∠ADC,
∴∠ADE=∠CDE,
∵?ABCD中,AD∥BC,
∴∠ADE=∠CED,
∴∠CDE=∠CED,
∴CE=CD,
∵在?ABCD中,AD=6,
∴AD=BC=6,
∴CE=BC﹣BE=7﹣2=4,
∴CD=AB=7,
∴?ABCD的周长=6+6+4+4=20.
故选:C.
12.如图,已知△ABC中,AB=AC,AE是∠BAC的外角平分线,ED∥AB交AC于点G
①AD⊥BC;②AE∥BC;③AE=AG2+AE2=4AG2.
其中正确结论的个数是( )
A.1
B.2
C.3
D.4
【分析】连接EC,根据等腰三角形的性质得出AD⊥BC,即可判断①;求出∠FAE=∠B,再根据平行线的性质得出AE∥BC,即可判断②;求出四边形ABDE是平行四边形,根据平行四边形的性质得出AE=BD,求出AE=CD,根据矩形的判定推出四边形ADCE是矩形,根据矩形的性质得出AC=DE,AG=CG,DG=EG,求出DG=AG=CG=EG,根据勾股定理判断④即可;根据AE=BD=BC和AG=AC判断③即可.
【解答】解:连接EC,
∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,故①正确;
∵AB=AC,
∴∠B=∠ACB,
∵AE平分∠FAC,
∴∠FAC=2∠FAE,
∵∠FAC=∠B+∠ACB,
∴∠FAE=∠B,
∴AE∥BC,故②正确;
∵AE∥BC,DE∥AB,
∴四边形ABDE是平行四边形,
∴AE=BD,
∵AB=AC,AD⊥BC,
∴CD=BD,
∴AE=CD,
∵AE∥BC,∠ADC=90°,
∴四边形ADCE是矩形,
∴AC=DE,AG=CG,
∴DG=AG=CG=EG,
在Rt△AED中,AD2+AE3=DE2=AC2=(6AG)2=4AG2,故④正确;
∵AE=BD=BCAC,
∴AG=AE错误(已知没有条件AC=BC),故③错误;
即正确的个数是3个,
故选:C.
二、填空题(本大题共4个小题,每小题3分,共12分)
13.一个n边形的各内角都等于120°,则边数n是 6 .
【分析】首先求出外角度数,再用360°除以外角度数可得答案.
【解答】解:∵n边形的各内角都等于120°,
∴每一个外角都等于180°﹣120°=60°,
∴边数n=360°÷60°=6.
故答案为:6.
14.若菱形的两条对角线长分别是6和8,则此菱形的周长是 20 ,面积是 24 .
【分析】首先根据题意画出图形,然后由菱形的两条对角线长分别是6和8,可求得OA=4,OB=3,再由勾股定理求得边长,继而求得此菱形的周长与面积.
【解答】解:如图,菱形ABCD中,BD=6,
∴OA=AC=4BD=3,
∴AB==5,
∴此菱形的周长是:5×8=20,面积是:.
故答案为:20,24.
15.已知直角三角形的长为3cm、5cm,则第三边长为 或4 cm.
【分析】分类讨论:①当5为直角边时,②当5为斜边时,根据勾股定理依次求出答案即可.
【解答】解:①当5是直角边时,斜边==;
②当7为斜边时,此时第三边=.
综上可得,第三边的长度为.
故答案为:或4.
16.如图,在矩形ABCD中,AB=10,动点P满足S△PAB=S矩形ABCD,则点P到A,B两点距离之和PA+PB的最小值为 2 .
【分析】首先由S△PAB=S矩形ABCD,得出动点P在与AB平行且与AB的距离是4的直线l上,作A关于直线l的对称点E,连接AE,连接BE,则BE的长就是所求的最短距离.然后在直角三角形ABE中,由勾股定理求得BE的值,即PA+PB的最小值.
【解答】解:设△ABP中AB边上的高是h.
∵S△PAB=S矩形ABCD,
∴AB?h=,
∴h=AD=7,
∴动点P在与AB平行且与AB的距离是2的直线l上,如图,连接AE,则BE的长就是所求的最短距离.
在Rt△ABE中,∵AB=10,
∴BE===7,
即PA+PB的最小值为2.
故答案为:2.
三、解答题(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题6分,第22、23题每小题6分,第24、25题每小题6分,共72分,解答应写出必要的文字说明、证明过程或演算步骤)
17.(6分)(1)分解因式:3x2y﹣6xy+3y;
(2)化简:.
【分析】(1)先题公因式,再用公式分解.
(2)先算括号内,再算括号外.
【解答】解:(1)原式=3y(x2﹣8x+1)
=3y(x﹣5)2.
(2)原式=(+)×
=×
=.
18.(6分)计算:
(1);
(2).
【分析】(1)先根据零指数幂,二次根式的性质,有理数的乘方,二次根式的乘法进行计算,再求出答案即可;
(2)先根据二次根式的乘法和除法进行计算,再求出答案即可.
【解答】解:(1)原式=1+2+9﹣2
=10;
(2)原式=3﹣1+
=2+
=7+2.
19.(6分)解下列分式方程:
(1);
(2).
【分析】将分式方程化为整式方程,解整式方程然后检验即可.
【解答】解:(1)方程两边都乘以5x(x+2)得:8(x+2)=5x,
解得:x=6,
经检验,x=3是原方程的根.
(2)方程两边都乘以(x﹣1)得8x﹣1﹣(x﹣1)=2,
解得:x=,
经检验,x=.
20.(8分)在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形),C的坐标分别为A(﹣3,5),C(0,3).
(1)请在如图所示的网格内作出ABC关于y轴对称的△A1B1C1.
(2)写出点B1的坐标并求出△A1B1C1的面积.
【分析】(1)分别作出A,B,C的对应点A1,B1,C1即可.
(2)利用分割法求解即可.
【解答】解:(1)如图,称的△A1B1C2即为所求作.
(2)点B1的坐标(1,3)1B1C4的面积=3×4﹣×1×7﹣×2×3=4.
21.(8分)如图所示,在四边形ABDC中,∠A=90°,AC=12,BD=8
(1)连接BC,求BC的长;
(2)判断△BCD的形状,并说明理由.
【分析】(1)直接利用勾股定理得出BC的长;
(2)直接利用勾股定理逆定理进而分析得出答案.
【解答】解:(1)∵∠A=90°,
∴BC===15;
(2)△BCD是直角三角形,
理由:∵BC2=155=225,
BD2=85=64,
CD2=172=289,
∴BC8+BD2=CD2=289,
∴△BCD是直角三角形.
22.(9分)为迎接元旦,某花店老板决定将玫瑰花每枝降价1元促销,降价后
(1)求降价后每枝玫瑰花的售价是多少?(用分式方程解答)
(2)根据销售情况,店主用不多于900元的资金购进了康乃馨和玫瑰两种鲜花共500枝,康乃馨进价为2元/枝,问至少要购进玫瑰花多少枝?
【分析】(1)可设降价后每枝玫瑰的售价是x元,根据等量关系:降价后30元可购买玫瑰的数量=原来购买玫瑰数量的1.5倍,列出方程求解即可;
(2)可设购进玫瑰y枝,根据不等量关系:购进康乃馨的钱数+购进玫瑰的钱数≤900元,列出不等式求解即可.
【解答】解:(1)设降价后每枝玫瑰的售价是x元,
由题意可得:×1.8,
解得:x=2.
经检验,x=2是原方程的解.
答:降价后每枝玫瑰的售价是4元.
(2)设购进玫瑰y枝,依题意有
2(500﹣y)+1.5y≤900,
解得:y≥200.
答:至少购进玫瑰200枝.
23.(9分)如图,正方形ABCD,点E,CD上,且DE=CF
(1)求证:BE=AF;
(2)若AB=4,DE=1,求AG的长.
【分析】(1)由正方形的性质得出∠BAE=∠ADF=90°,AB=AD=CD,得出AE=DF,由SAS证明△BAE≌△ADF,即可得出结论;
(2)由全等三角形的性质得出∠EBA=∠FAD,得出∠GAE+∠AEG=90°,因此∠AGE=90°,由勾股定理得出BE==5,在Rt△ABE中,由三角形面积即可得出结果.
【解答】(1)证明:∵四边形ABCD是正方形,
∴∠BAE=∠ADF=90°,AB=AD=CD,
∵DE=CF,
∴AE=DF,
在△BAE和△ADF中,,
∴△BAE≌△ADF(SAS),
∴BE=AF;
(2)解:由(1)得:△BAE≌△ADF,
∴∠EBA=∠FAD,
∴∠GAE+∠AEG=90°,
∴∠AGE=90°,
∵AB=4,DE=1,
∴AE=6,
∴BE===5,
在Rt△ABE中,AB×AE=,
∴AG==.
24.(10分)如图,在△ABC中,AB=AC=20cm,且BD=16cm.点M从点A出发,沿AC方向匀速运动;同时点P由B点出发,沿BA方向匀速运动,过点P的直线PQ∥AC,交BC于点Q,设运动时间为t(s)(0<t<5),解答下列问题:
(1)线段AD= 12 cm;
(2)求证:PB=PQ;
(3)当t为何值时,以P、Q、D、M为顶点的四边形是平行四边形?
【分析】(1)由勾股定理求出AD即可;
(2)由等腰三角形的性质和平行线的性质得出∠PBQ=∠PQB,再由等腰三角形的判定定理即可得出结论;
(3)分两种情况:①当点M在点D的上方时,PQ=BP=t,AM=4t,AD=12,得出MD=AD﹣AM=12﹣4t,由PQ∥MD,当PQ=MD时,四边形PQDM是平行四边形,得出方程,解方程即可;
②当点M在点D的下方时,PQ=BP=t,AM=4t,AD=12,得出MD=AM﹣AD=4t﹣12,由PQ∥MD,当PQ=MD时,四边形PQDM是平行四边形,得出方程,解方程即可.
【解答】(1)解:在Rt△ABD中,由勾股定理得:AD==,
故答案为:12;
(2)证明:如图2所示:
∵AB=AC,
∴∠ABC=∠C,即∠PBQ=∠C,
∵PQ∥AC,
∴∠PQB=∠C,
∴∠PBQ=∠PQB,
∴PB=PQ;
(3)解:分两种情况:
①当点M在点D的上方时,如图2所示:
由题意得:PQ=BP=t,AM=4t,
∴MD=AD﹣AM=12﹣6t,
∵PQ∥AC,
∴PQ∥MD,
∴当PQ=MD时,四边形PQDM是平行四边形,
即:当t=12﹣4t时,四边形PQDM是平行四边形,
解得:(s);
②当点M在点D的下方时,如图6所示:
根据题意得:PQ=BP=t,AM=4t,
∴MD=AM﹣AD=4t﹣12,
∵PQ∥AC,
∴PQ∥MD,
∴当PQ=MD时,四边形PQDM是平行四边形,
即:当t=6t﹣12时,四边形PQDM是平行四边形,
解得:t=4(s);
综上所述,当t=,以P、Q、D.
25.(10分)如图,在?ABCD中,∠BAD的平分线交BC于点E,以EC、CF为邻边作?ECFG.
(1)证明?ECFG是菱形;
(2)若∠ABC=120°,连接BD、CG,求∠BDG的度数;
(3)若∠ABC=90°,AB=6,AD=8,求DM的长.
【分析】(1)平行四边形的性质可得AD∥BC,AB∥CD,再根据平行线的性质证明∠CEF=∠CFE,根据等角对等边可得CE=CF,再有条件四边形ECFG是平行四边形,可得四边形ECFG为菱形,即可解决问题;
(2)先判断出∠BEG=120°=∠DCG,再判断出AB=BE,进而得出BE=CD,即可判断出△BEG≌△DCG(SAS),再判断出∠CGE=60°,进而得出△BDG是等边三角形,即可得出结论;
(3)首先证明四边形ECFG为正方形,再证明△BME≌△DMC可得DM=BM,∠DMC=∠BME,再根据∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°可得到△BDM是等腰直角三角形,由等腰直角三角形的性质即可得到结论.
【解答】解:(1)证明:
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG=,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△BEG≌△DCG(SAS),
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)如图4中,连接BM,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=6,AD=8,
∴BD=10,
∴DM=BD=5.
同课章节目录
