2020-2021学年辽宁省沈阳市皇姑区虹桥中学九年级下期月考数学试卷(3月份)(五四学制)(word版含解析)
文档属性
| 名称 | 2020-2021学年辽宁省沈阳市皇姑区虹桥中学九年级下期月考数学试卷(3月份)(五四学制)(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 411.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-02 00:00:00 | ||
图片预览


文档简介
2020-2021学年辽宁省沈阳市皇姑区虹桥中学九年级(下)月考数学试卷(3月份)(五四学制)
一、选择(每题2分,共20分)
1.下列各数是无理数的是( )
A.0
B.﹣1
C.
D.
2.下列计算正确的是( )
A.a2+2a2=3a4
B.a6÷a3=a2
C.(a﹣b)2=a2﹣b2
D.(ab)2=a2b2
3.如果将一组数据中的每个数都减去5,那么所得的一组新数据( )
A.众数改变,方差改变
B.众数不变,平均数改变
C.中位数改变,方差不变
D.中位数不变,平均数不变
4.在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数最有可能是( )
A.5
B.10
C.12
D.15
5.已知一组数据:3,4,6,7,8,8,下列说法正确的是( )
A.众数是2
B.众数是8
C.中位数是6
D.中位数是7
6.无理数3﹣3在( )
A.3和4之间
B.4和5之间
C.5和6之间
D.6和7之间
7.四边形ABCD的对角线AC、BD互相平分,要使它成为矩形,需要添加的条件是( )
A.AB=CD
B.AC=BD
C.AB=BC
D.AC⊥BD
8.已知扇形的半径为12,圆心角为60°,则这个扇形的弧长为( )
A.9π
B.6π
C.3π
D.4π
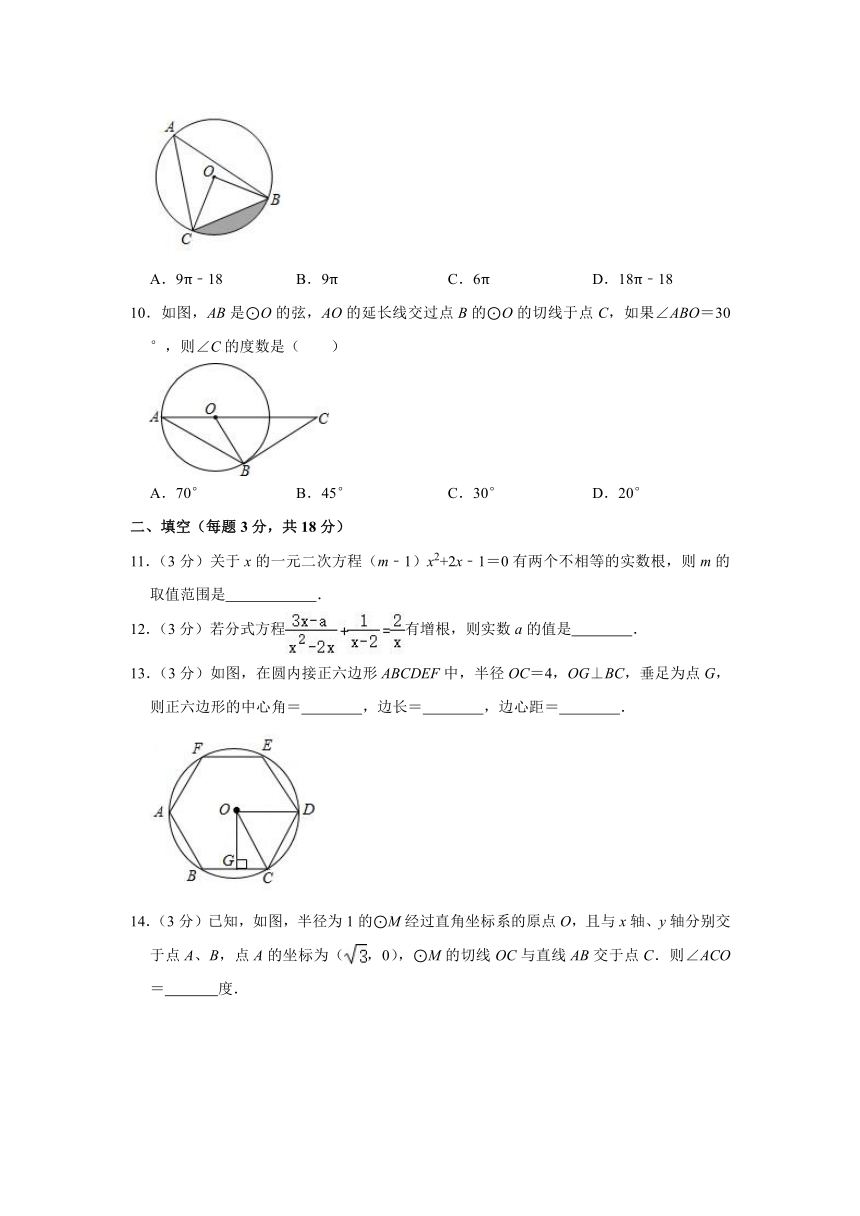
9.如图,△ABC外接圆⊙O的半径长为6,若∠A=45°.则阴影部分的面积为( )
A.9π﹣18
B.9π
C.6π
D.18π﹣18
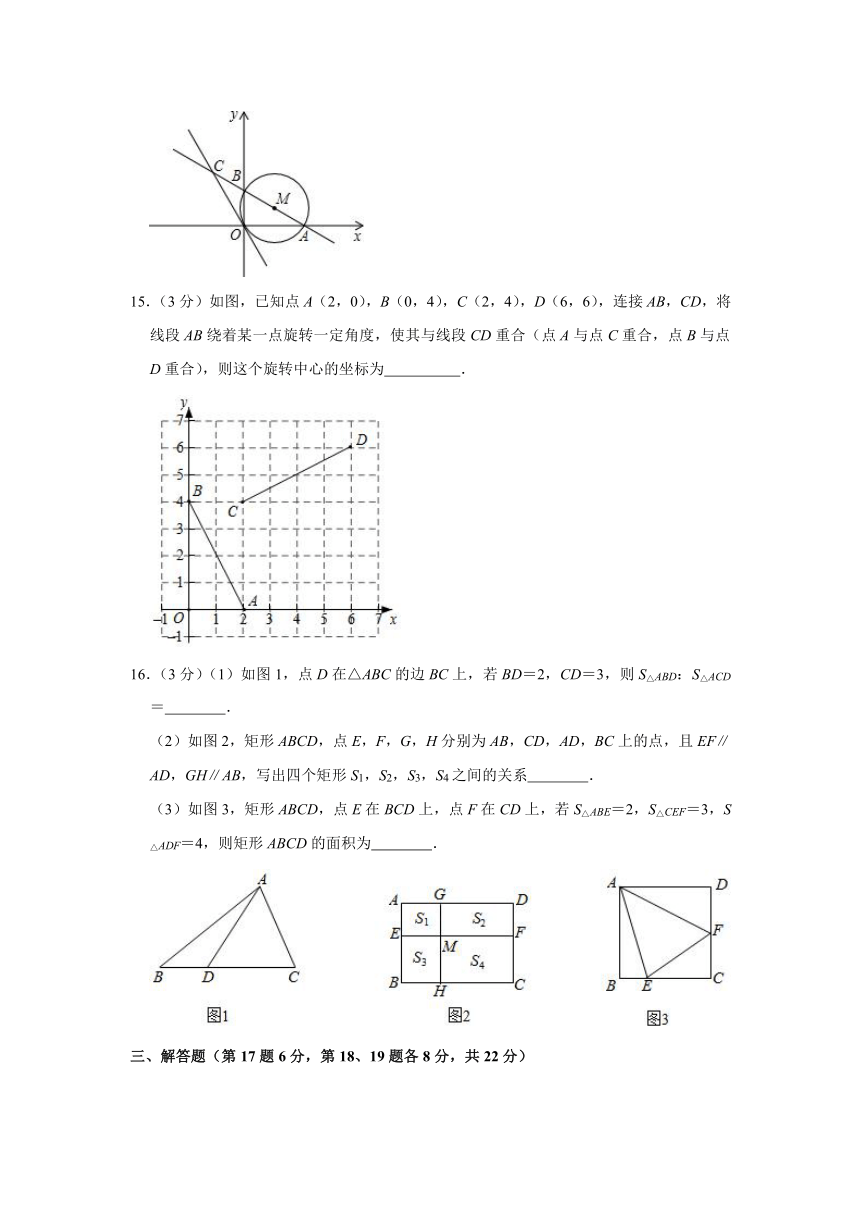
10.如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=30°,则∠C的度数是( )
A.70°
B.45°
C.30°
D.20°
二、填空(每题3分,共18分)
11.(3分)关于x的一元二次方程(m﹣1)x2+2x﹣1=0有两个不相等的实数根,则m的取值范围是
.
12.(3分)若分式方程有增根,则实数a的值是
.
13.(3分)如图,在圆内接正六边形ABCDEF中,半径OC=4,OG⊥BC,垂足为点G,则正六边形的中心角=
,边长=
,边心距=
.
14.(3分)已知,如图,半径为1的⊙M经过直角坐标系的原点O,且与x轴、y轴分别交于点A、B,点A的坐标为(,0),⊙M的切线OC与直线AB交于点C.则∠ACO=
度.
15.(3分)如图,已知点A(2,0),B(0,4),C(2,4),D(6,6),连接AB,CD,将线段AB绕着某一点旋转一定角度,使其与线段CD重合(点A与点C重合,点B与点D重合),则这个旋转中心的坐标为
.
16.(3分)(1)如图1,点D在△ABC的边BC上,若BD=2,CD=3,则S△ABD:S△ACD=
.
(2)如图2,矩形ABCD,点E,F,G,H分别为AB,CD,AD,BC上的点,且EF∥AD,GH∥AB,写出四个矩形S1,S2,S3,S4之间的关系
.
(3)如图3,矩形ABCD,点E在BCD上,点F在CD上,若S△ABE=2,S△CEF=3,S△ADF=4,则矩形ABCD的面积为
.
三、解答题(第17题6分,第18、19题各8分,共22分)
17.(6分)计算:(π﹣4)0+|3﹣tan60°|﹣()﹣2+.
18.(8分)某单位食堂为全体960名职工提供了A,B,C,D四种套餐,为了解职工对这四种套餐的喜好情况.单位随机抽取240名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问卷调查.根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
(1)在抽取的240人中最喜欢A套餐的人数为
.
(2)扇形统计图中“B”占m%,则m=
.
(3)扇形统计图中“C”对应扇形的圆心角的大小为
.
(4)依据本次调查的结果,估计全体960名职工中最喜欢D套餐的人数.
19.(8分)某单位食堂为全体职工提供了套餐服务,“食品安全监督员”准备在甲、乙、丙、丁四名职工中选出.
(1)若只有1人担任“食品安全监督员”,则甲被选中的概率为
.
(2)若有2人担任“食品安全监督员”,求甲被选中的概率.
四、解答题(共2小题,满分16分)
20.(8分)如图,点D,E分别是△ABC的边AB,AC的中点,连接BE,过点C作CF∥BE,交DE的延长线于点F,若EF=3,求DE的长.
21.(8分)为推进垃圾分类,推动绿色发展.某化工厂要购进甲、乙两种型号机器人来进行垃圾分类.用360万元购买甲型机器人和用480万元购买乙型机器人的台数相同,两种型号机器人的单价和为140万元,求设甲型机器人单价.
五、(本题10分)
22.(10分)如图,⊙O是△ABC的外接圆,∠ABC=45°,OC∥AD,AD交BC的延长线于D,AB交OC于E.
(1)求证:AD是⊙O的切线;
(2)若AE=2,CE=2.求⊙O的半径和线段BE的长.
六、解答题(共1小题,满分10分)
23.(10分)如图,已知AB为⊙O的直径,AB=12,点C和点D是⊙O上关于直线AB对称的两个点,连接OC、AC.且∠BOC<90°.直线BC和直线AD相交于点E,过点C作直线CG与线段AB的延长线相交于点F,与直线AD相交于点G.且∠GAF=∠GCE.
(1)求证:直线CG为⊙O的切线;
(2)若点H为线段OB上一点,迄接CH,满足CB=CH,求OH+HC的最大值.
七、(本题12分)
24.(12分)(1)如图1,等腰直角△ABC,∠B=90°,点D为AC的中点,点E为边AB上的一点,作DE垂直DF交BC于点F,求证:DE=DF.
(2)如图2,等腰直角△ABC,∠B=90°,点D为AC的中点,点E为边AB上的一点,线段DE绕着点D逆时针旋转90°得到线段DF,求证:点F在线段BC上;
(3)如图3,直角△ABC,点D为AC的中点,点E为边AB上的一点,线段DE绕着点D逆时针旋转90°得到线段DF,若AB=6,BC=8,
①直接写出线段EF=时,BE的长;
②直接写出△ACF是等腰三角形时,BE的长;
③直接写出△BEF面积的最大值.
八、(本题12分)
25.(12分)已知抛物线y=ax2+bx+6(a≠0)交x轴于点A(6,0)和点B(﹣1,0),交y轴于点C.
(1)求抛物线的解析式和顶点坐标;
(2)如图(1),点P是抛物线上位于直线AC上方的动点,过点P分别作x轴、y轴的平行线,交直线AC于点D,E,当PD+PE取最大值时,求点P的坐标;
(3)如图(2),点M为抛物线对称轴l上一点,点N为抛物线上一点,当直线AC垂直平分△AMN的边MN时,求点N的坐标.
2020-2021学年辽宁省沈阳市皇姑区虹桥中学九年级(下)月考数学试卷(3月份)(五四学制)
参考答案与试题解析
一、选择(每题2分,共20分)
1.下列各数是无理数的是( )
A.0
B.﹣1
C.
D.
【分析】根据无理数是无限不循环小数,可得答案.
【解答】解:0,﹣1,是有理数,是无理数,
故选:C.
2.下列计算正确的是( )
A.a2+2a2=3a4
B.a6÷a3=a2
C.(a﹣b)2=a2﹣b2
D.(ab)2=a2b2
【分析】根据合并同类项法则、同底数幂的乘除法、幂的乘方积的乘方以及完全平方公式进行计算即可.
【解答】解:a2+2a2=3a2,因此选项A不符合题意;
a6÷a3=a6﹣3=a3,因此选项B不符合题意;
(a﹣b)2=a2﹣2ab+b2,因此选项C不符合题意;
(ab)2=a2b2,因此选项D符合题意;
故选:D.
3.如果将一组数据中的每个数都减去5,那么所得的一组新数据( )
A.众数改变,方差改变
B.众数不变,平均数改变
C.中位数改变,方差不变
D.中位数不变,平均数不变
【分析】由每个数都减去5,那么所得的一组新数据的众数、中位数、平均数都减少5,方差不变,据此可得答案.
【解答】解:如果将一组数据中的每个数都减去5,那么所得的一组新数据的众数、中位数、平均数都减少5,方差不变,
故选:C.
4.在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数最有可能是( )
A.5
B.10
C.12
D.15
【分析】设袋子中红球有x个,根据摸出红球的频率稳定在0.25左右列出关于x的方程,求出x的值,从而得出答案.
【解答】解:设袋子中红球有x个,
根据题意,得:=0.25,
解得x=5,
∴袋子中红球的个数最有可能是5个,
故选:A.
5.已知一组数据:3,4,6,7,8,8,下列说法正确的是( )
A.众数是2
B.众数是8
C.中位数是6
D.中位数是7
【分析】根据众数和中位数的定义求解.
【解答】解:数据:3,4,6,7,8,8的众数为8,中为数为6.5.
故选:B.
6.无理数3﹣3在( )
A.3和4之间
B.4和5之间
C.5和6之间
D.6和7之间
【分析】先估算出3的范围,再估算3﹣3的值.
【解答】解:,
∵81<99<100,
∴,
∴,
故无理数3﹣3在6和7之间.
故选:D.
7.四边形ABCD的对角线AC、BD互相平分,要使它成为矩形,需要添加的条件是( )
A.AB=CD
B.AC=BD
C.AB=BC
D.AC⊥BD
【分析】由平行四边形的判定方法得出四边形ABCD是平行四边形,再由矩形的判定方法即可得出结论.
【解答】解:需要添加的条件是AC=BD;理由如下:
∵四边形ABCD的对角线AC、BD互相平分,
∴四边形ABCD是平行四边形,
∵AC=BD,
∴四边形ABCD是矩形(对角线相等的平行四边形是矩形);
故选:B.
8.已知扇形的半径为12,圆心角为60°,则这个扇形的弧长为( )
A.9π
B.6π
C.3π
D.4π
【分析】把扇形的圆心角为和半径为代入弧长公式计算即可.
【解答】解:依题意,n=60,r=12,
∴扇形的弧长===4π.
故选:D.
9.如图,△ABC外接圆⊙O的半径长为6,若∠A=45°.则阴影部分的面积为( )
A.9π﹣18
B.9π
C.6π
D.18π﹣18
【分析】由∠A=45°得出∠BOC=90°,再分别算出三角形OBC与扇形OBC的面积作差求解.
【解答】解:∵∠A=45°,
∴∠BOC=2∠A=90°,
∵⊙O的半径长为6,
∴S△BOC=OC?OB=18.
又∵S扇形OBC==9π,
∴阴影部分的面积为S扇形OBC﹣S△BOC=9π﹣18.
故选:A.
10.如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=30°,则∠C的度数是( )
A.70°
B.45°
C.30°
D.20°
【分析】由BC是⊙O的切线,OB是⊙O的半径,得到∠OBC=90°,根据等腰三角形的性质得到∠A=∠ABO=30°,由外角的性质得到∠BOC=60°,即可求得∠C=30°.
【解答】解:∵BC是⊙O的切线,OB是⊙O的半径,
∴∠OBC=90°,
∵OA=OB,
∴∠A=∠ABO=30°,
∴∠BOC=60°,
∴∠C=30°.
故选:C.
二、填空(每题3分,共18分)
11.(3分)关于x的一元二次方程(m﹣1)x2+2x﹣1=0有两个不相等的实数根,则m的取值范围是 m>0且m≠1 .
【分析】根据一元二次方程的定义和判别式的意义得到m﹣1≠0且△=22﹣4(m﹣1)×(﹣1)>0,然后求出两个不等式的公共部分即可.
【解答】解:根据题意得m﹣1≠0且△=22﹣4(m﹣1)×(﹣1)>0,
解得m>0且m≠1.
故答案为:m>0且m≠1.
12.(3分)若分式方程有增根,则实数a的值是 4或8 .
【分析】对分式方程+=进行正常求解,化简为2x=a﹣4,当x=0或x=2时,分式方程有增根,在x=0和x=2时,分别求出a的值即可.
【解答】解:∵+=,
∴+=,
当x2﹣2x≠0时,
原式化为3x﹣a+x=2x﹣4,
∴2x=a﹣4,
∵分式方程有增根,
∴x=0或x=2,
当x=0时,a=4;
当x=2时,a=8.
故答案是4或8.
13.(3分)如图,在圆内接正六边形ABCDEF中,半径OC=4,OG⊥BC,垂足为点G,则正六边形的中心角= 60° ,边长= 4 ,边心距= 2 .
【分析】由正六边形的性质得∠COD==60°,再证△OCD是等边三角形,得BC=CD=OC=4,再由垂径定理和含30°角的直角三角形的性质求出OG即可.
【解答】解:在圆内接正六边形ABCDEF中,∠COD==60°,
∵OC=OD,
∴△OCD是等边三角形,
∴BC=CD=OC=4,
∵OG⊥BC,
∴CG=BC=2,
∵∠COG=∠COD=30°,
∴OG=CG=2,
故答案为:60°,4,2.
14.(3分)已知,如图,半径为1的⊙M经过直角坐标系的原点O,且与x轴、y轴分别交于点A、B,点A的坐标为(,0),⊙M的切线OC与直线AB交于点C.则∠ACO= 30 度.
【分析】在Rt△AOB中,已知了直径AB和OA的长,即可求得∠OAB、∠OBA的度数;而由弦切角定理知∠OAB=∠BOC,进而可由三角形的外角性质求出∠ACO的度数.
【解答】解:∵AB=2,OA=,
∴cos∠BAO==,
∴∠OAB=30°,∠OBA=60°;
∵OC是⊙M的切线,
∴∠BOC=∠BAO=30°,
∴∠ACO=∠OBA﹣∠BOC=30°.
故答案为:30.
15.(3分)如图,已知点A(2,0),B(0,4),C(2,4),D(6,6),连接AB,CD,将线段AB绕着某一点旋转一定角度,使其与线段CD重合(点A与点C重合,点B与点D重合),则这个旋转中心的坐标为 (4,2) .
【分析】画出平面直角坐标系,作出线段AC,BD的垂直平分线的交点P,点P即为旋转中心.
【解答】解:平面直角坐标系如图所示,旋转中心是P点,P(4,2).
故答案为(4,2).
16.(3分)(1)如图1,点D在△ABC的边BC上,若BD=2,CD=3,则S△ABD:S△ACD= 2:3 .
(2)如图2,矩形ABCD,点E,F,G,H分别为AB,CD,AD,BC上的点,且EF∥AD,GH∥AB,写出四个矩形S1,S2,S3,S4之间的关系 = .
(3)如图3,矩形ABCD,点E在BCD上,点F在CD上,若S△ABE=2,S△CEF=3,S△ADF=4,则矩形ABCD的面积为 16 .
【分析】(1)由S△ABD:S△ACD=BD:CD作答.
(2)分别表示出用线段乘积表示S1,S2,S3,S4,然后作比求解.
(3)设BC=AD=x,AB=CD=y,用含xy代数式表示S△ABE,S△CEF,S△ADF与矩形面积解方程求解.
【解答】解:(1)△ABD与△ACD为同高三角形,设高为h,
∴S△ABD:S△ACD=BD?h:CD?h=BD:CD=2:3.
故答案为:2:3.
(2)∵S1=EM?GM,S2=MF?GM,S3=EM?MF,S4=MH?MF,
∴=,=,
∴=.
故答案为:=.
(3)设BC=AD=x,AB=CD=y,
∵S△ABE=2,S△CEF=3,S△ADF=4,
∴DF?x=8,BE?y=4,
∴(x﹣BE)(y﹣DF)=6,即xy﹣BE?y﹣DF?x+DF?BE=6,
将DF?x=8,BE?y=4代入可得xy+DF?BE=18①,
由①得DF?BE=18﹣xy②,
∵DF?x?BE?y=32③,
将②代入③可得(18﹣xy)?xy=32,
解得xy=16或xy=2(舍).
故答案为:16.
三、解答题(第17题6分,第18、19题各8分,共22分)
17.(6分)计算:(π﹣4)0+|3﹣tan60°|﹣()﹣2+.
【分析】直接利用零指数幂的性质以及负指数幂的性质和特殊角的三角函数值以及二次根式的性质分别化简得出答案.
【解答】解:(π﹣4)0+|3﹣tan60°|﹣()﹣2+
=1+3﹣﹣4+3
=2.
18.(8分)某单位食堂为全体960名职工提供了A,B,C,D四种套餐,为了解职工对这四种套餐的喜好情况.单位随机抽取240名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问卷调查.根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
(1)在抽取的240人中最喜欢A套餐的人数为 60 .
(2)扇形统计图中“B”占m%,则m= 35 .
(3)扇形统计图中“C”对应扇形的圆心角的大小为 108° .
(4)依据本次调查的结果,估计全体960名职工中最喜欢D套餐的人数.
【分析】(1)用被调查的职工人数乘以最喜欢A套餐人数所占百分比即可得其人数;
(2)用B套餐的人数除以总人数,即可得出m的值;
(3)先求出C对应人数,继而用360°乘以最喜欢C套餐人数所占比例即可得;
(4)用总人数乘以样本中最喜欢D套餐的人数所占比例即可得.
【解答】解:(1)在抽取的240人中最喜欢A套餐的人数为240×25%=60(人).
故答案为:60;
(2)m%=×100%=35%,即m=35.
故答案为:35;
(3)最喜欢C套餐的人数为240﹣(60+84+24)=72(人),
则扇形统计图中“C”对应扇形的圆心角的大小为360°×=108°,
故答案为:108°;
(4)根据题意得:
960×=96(人),
答:全体960名职工中最喜欢D套餐的人数有96人.
19.(8分)某单位食堂为全体职工提供了套餐服务,“食品安全监督员”准备在甲、乙、丙、丁四名职工中选出.
(1)若只有1人担任“食品安全监督员”,则甲被选中的概率为 .
(2)若有2人担任“食品安全监督员”,求甲被选中的概率.
【分析】(1)直接利用概率公式列式求解即可;
(2)列举出所有结果,利用概率公式列式求解即可.
【解答】解:∵共甲、乙、丙、丁四名职工,
∴甲被选中担任“食品安全监督员”的概率为,
故答案为:;
(2)若有2人担任“食品安全监督员”,则可能会出现的结果为甲乙、甲丙,甲丁,乙丙,乙丁,丙丁共六种结果,选中甲的有3中可能,
∴若有2人担任“食品安全监督员”,求甲被选中的概率=.
四、解答题(共2小题,满分16分)
20.(8分)如图,点D,E分别是△ABC的边AB,AC的中点,连接BE,过点C作CF∥BE,交DE的延长线于点F,若EF=3,求DE的长.
【分析】先证明DE为△ABC的中位线,得到四边形BCFE为平行四边形,求出BC=EF=3,根据中位线定理即可求解.
【解答】解:∵D、E分别是△ABC的边AB、AC的中点,
∴DE为△ABC的中位线,
∴DE∥BC,DE=BC,
∴EF∥BC,
∵CF∥BE,
∴四边形BCFE为平行四边形,
∴BC=EF=3,
∴DE=BC=.
21.(8分)为推进垃圾分类,推动绿色发展.某化工厂要购进甲、乙两种型号机器人来进行垃圾分类.用360万元购买甲型机器人和用480万元购买乙型机器人的台数相同,两种型号机器人的单价和为140万元,求设甲型机器人单价.
【分析】设甲种型号机器人每台的价格是x万元,根据“用360万元购买甲型机器人和用480万元购买乙型机器人的台数相同”,列出关于x的分式方程.
【解答】解:设甲型机器人每台x万元,
根据题意,可得:,
解得:x=60,
经检验,x=60是原分式方程的解,且符合题意,
答:甲型机器人每台60万元.
五、(本题10分)
22.(10分)如图,⊙O是△ABC的外接圆,∠ABC=45°,OC∥AD,AD交BC的延长线于D,AB交OC于E.
(1)求证:AD是⊙O的切线;
(2)若AE=2,CE=2.求⊙O的半径和线段BE的长.
【分析】(1)连接OA,根据切线的性质得到OA⊥AD,再根据圆周角定理得到∠AOC=2∠ABC=90°,然后根据平行线的判定即可得到结论;
(2)设⊙O的半径为R,则OA=R,OE=R﹣2,AE=2,在Rt△OAE中根据勾股定理可计算出R=4;设⊙O的半径为R,延长CO交⊙O于F,连接AF,GJ
相似三角形的性质即可得到结论.
【解答】(1)证明:连接OA,如图,
∵AD是⊙O的切线,
∴OA⊥AD,
∵∠AOC=2∠ABC=2×45°=90°,
∴OA⊥OC,
∴AD∥OC,
∴OA⊥AD,
∴AD是⊙O的切线
(2)解:设⊙O的半径为R,则OA=R,OE=R﹣2,AE=2,
在Rt△OAE中,∵AO2+OE2=AE2,
∴R2+(R﹣2)2=(2)2,解得R=1,(负值舍去),
延长CO交⊙O于F,连接AF,
则△CEB∽△AEF,
∴,
∵EF=2R﹣2=2,
∴BE=.
六、解答题(共1小题,满分10分)
23.(10分)如图,已知AB为⊙O的直径,AB=12,点C和点D是⊙O上关于直线AB对称的两个点,连接OC、AC.且∠BOC<90°.直线BC和直线AD相交于点E,过点C作直线CG与线段AB的延长线相交于点F,与直线AD相交于点G.且∠GAF=∠GCE.
(1)求证:直线CG为⊙O的切线;
(2)若点H为线段OB上一点,迄接CH,满足CB=CH,求OH+HC的最大值.
【分析】(1)由题意可知:∠CAB=∠GAF,由圆的性质可知:∠CAB=∠OCA,所以∠OCA=∠GCE,从而可证明直线CG是⊙O的切线;
(2)由于CB=CH,所以∠CBH=∠CHB,易证∠CBH=∠OCB,从而可证明△CBH∽△OBC,可得=,所以HB=,由于BC=HC,所以OH+HC=6﹣+BC,利用二次函数的性质即可求出OH+HC的最大值.
【解答】解:(1)由题意可知:∠CAB=∠GAF,
∵AB是⊙O的直径,
∴∠ACB=90°
∵OA=OC,
∴∠CAB=∠OCA,
∴∠OCA+∠OCB=90°,
∵∠GAF=∠GCE,
∴∠GCE+∠OCB=∠OCA+∠OCB=90°,
∵OC是⊙O的半径,
∴直线CG是⊙O的切线.
(2)∵CB=CH,
∴∠CBH=∠CHB,
∵OB=OC,
∴∠CBH=∠OCB,
∴△CBH∽△OBC,
∴=,
∵AB=12,
∴BC2=HB?OC=6HB,
∴HB=,
∴OH=OB﹣HB=6﹣,
∵CB=CH,
∴OH+HC=6﹣+BC,
当∠BOC=90°,
此时BC=6,
∵∠BOC<90°,
∴0<BC<6,
令BC=x,
∴OH+HC=﹣(x﹣3)2+,
当x=3时,
∴OH+HC可取得最大值,最大值为.
七、(本题12分)
24.(12分)(1)如图1,等腰直角△ABC,∠B=90°,点D为AC的中点,点E为边AB上的一点,作DE垂直DF交BC于点F,求证:DE=DF.
(2)如图2,等腰直角△ABC,∠B=90°,点D为AC的中点,点E为边AB上的一点,线段DE绕着点D逆时针旋转90°得到线段DF,求证:点F在线段BC上;
(3)如图3,直角△ABC,点D为AC的中点,点E为边AB上的一点,线段DE绕着点D逆时针旋转90°得到线段DF,若AB=6,BC=8,
①直接写出线段EF=时,BE的长;
②直接写出△ACF是等腰三角形时,BE的长;
③直接写出△BEF面积的最大值.
【分析】(1)证明:如图1中,连接BD.证明△EDB≌△FDC(ASA),可得结论.
(2)如图2中,连接DB,CF.证明△EDB≌△FDC(SAS),推出∠DBE=∠DCF=45°,推出点F在线段BC上.
(3)①如图3﹣1中,过点D作DT⊥AB于T.解直角三角形求出ET可得结论.
②证明△AFC是等腰直角三角形,推出点E与A重合,可得结论.
③如图3﹣3中,过点D作DT⊥AB于T,过点F作FR⊥DT于R.证明△DTE≌△FRD(AAS),推出ET=DR,DT=FR=4,设ET=DR=m,则RT=4﹣m,构建二次函数,可得结论.
【解答】(1)证明:如图1中,连接BD.
∵△ABC是等腰直角三角形,AD=DC,
∴BD⊥AC,BD=DA=DC,
∴BD⊥AC,
∵ED⊥DF,
∴∠EDF=∠BDC=90°,
∴∠EDB=∠FDC,
∵∠DBE=∠C=45°,
∴△EDB≌△FDC(ASA),
∴DE=DF.
(2)证明:如图2中,连接DB,CF.
∵∠BDC=∠EDF=90°,
∴∠BDE=∠CDF,
∵DB=DC,DE=DF,
∴△EDB≌△FDC(SAS),
∴∠DBE=∠DCF=45°,
∴点F在线段BC上.
(3)①如图3﹣1中,过点D作DT⊥AB于T.
∵∠ATD=∠ABC=90°,
∴DT∥CB,
∵AD=DC,
∴AT=TB=3,
∴DT=BC=4,
∵△DEF是等腰直角三角形,EF=,
∴DE=DF=,
∴ET===1,
∴BE=TB+ET=3+1=4,
当点E在点T的下方时,BE=3﹣1=2,
综上所述,满足条件的BE的值为4或2.
②如图3﹣2中,
∵△ACF是等腰三角形,
又∵AD=DC=DF,
∴∠AFC=90°,
∴△AFC是等腰直角三角形,
∴点E与A重合,
∴BE=6.
③如图3﹣3中,过点D作DT⊥AB于T,过点F作FR⊥DT于R.
∵∠DTE=∠FRD=90°,∠EDT=∠DFR,DE=DF,
∴△DTE≌△FRD(AAS),
∴ET=DR,DT=FR=4,
设ET=DR=m,则RT=4﹣m,
∴S△EFB=(3+m)(4﹣m)=(﹣m2+m+12)=﹣(m﹣)2+,
∵﹣<0,
∴△BEF的面积有最大值,最大值为.
八、(本题12分)
25.(12分)已知抛物线y=ax2+bx+6(a≠0)交x轴于点A(6,0)和点B(﹣1,0),交y轴于点C.
(1)求抛物线的解析式和顶点坐标;
(2)如图(1),点P是抛物线上位于直线AC上方的动点,过点P分别作x轴、y轴的平行线,交直线AC于点D,E,当PD+PE取最大值时,求点P的坐标;
(3)如图(2),点M为抛物线对称轴l上一点,点N为抛物线上一点,当直线AC垂直平分△AMN的边MN时,求点N的坐标.
【分析】(1)将点A,B坐标代入抛物线解析式中,解方程组即可得出结论;
(2)先求出OA=OC=6,进而得出∠OAC=45°,进而判断出PD=PE,即可得出当PE的长度最大时,PE+PD取最大值,设出点E坐标,表示出点P坐标,建立PE=﹣t2+6t=﹣(t﹣3)2+9,即可得出结论;
(3)先判断出NF∥x轴,进而求出点N的纵坐标,即可建立方程求解得出结论.
【解答】解:(1)∵抛物线y=ax2+bx+6经过点A(6,0),B(﹣1,0),
∴,
∴,
∴抛物线的解析式为y=﹣x2+5x+6=﹣(x﹣)2+,
∴抛物线的解析式为y=﹣x2+5x+6,顶点坐标为(,);
(2)由(1)知,抛物线的解析式为y=﹣x2+5x+6,
∴C(0,6),
∴OC=6,
∵A(6,0),
∴OA=6,
∴OA=OC,
∴∠OAC=45°,
∵PD平行于x轴,PE平行于y轴,
∴∠DPE=90°,∠PDE=∠DAO=45°,
∴∠PED=45°,
∴∠PDE=∠PED,
∴PD=PE,
∴PD+PE=2PE,
∴当PE的长度最大时,PE+PD取最大值,
∵A(6,0),C(0,6),
∴直线AC的解析式为y=﹣x+6,
设E(t,﹣t+6)(0<t<6),则P(t,﹣t2+5t+6),
∴PE=﹣t2+5t+6﹣(﹣t+6)=﹣t2+6t=﹣(t﹣3)2+9,
当t=3时,PE最大,此时,﹣t2+5t+6=12,
∴P(3,12);
(3)如图(2),设直线AC与抛物线的对称轴l的交点为F,连接NF,
∵点F在线段MN的垂直平分线AC上,
∴FM=FN,∠NFC=∠MFC,
∵l∥y轴,
∴∠MFC=∠OCA=45°,
∴∠MFN=∠NFC+∠MFC=90°,
∴NF∥x轴,
由(2)知,直线AC的解析式为y=﹣x+6,
当x=时,y=,
∴F(,),
∴点N的纵坐标为,
设N的坐标为(m,﹣m2+5m+6),
∴﹣m2+5m+6=,解得,m=或m=,
∴点N的坐标为(,)或(,).
一、选择(每题2分,共20分)
1.下列各数是无理数的是( )
A.0
B.﹣1
C.
D.
2.下列计算正确的是( )
A.a2+2a2=3a4
B.a6÷a3=a2
C.(a﹣b)2=a2﹣b2
D.(ab)2=a2b2
3.如果将一组数据中的每个数都减去5,那么所得的一组新数据( )
A.众数改变,方差改变
B.众数不变,平均数改变
C.中位数改变,方差不变
D.中位数不变,平均数不变
4.在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数最有可能是( )
A.5
B.10
C.12
D.15
5.已知一组数据:3,4,6,7,8,8,下列说法正确的是( )
A.众数是2
B.众数是8
C.中位数是6
D.中位数是7
6.无理数3﹣3在( )
A.3和4之间
B.4和5之间
C.5和6之间
D.6和7之间
7.四边形ABCD的对角线AC、BD互相平分,要使它成为矩形,需要添加的条件是( )
A.AB=CD
B.AC=BD
C.AB=BC
D.AC⊥BD
8.已知扇形的半径为12,圆心角为60°,则这个扇形的弧长为( )
A.9π
B.6π
C.3π
D.4π
9.如图,△ABC外接圆⊙O的半径长为6,若∠A=45°.则阴影部分的面积为( )
A.9π﹣18
B.9π
C.6π
D.18π﹣18
10.如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=30°,则∠C的度数是( )
A.70°
B.45°
C.30°
D.20°
二、填空(每题3分,共18分)
11.(3分)关于x的一元二次方程(m﹣1)x2+2x﹣1=0有两个不相等的实数根,则m的取值范围是
.
12.(3分)若分式方程有增根,则实数a的值是
.
13.(3分)如图,在圆内接正六边形ABCDEF中,半径OC=4,OG⊥BC,垂足为点G,则正六边形的中心角=
,边长=
,边心距=
.
14.(3分)已知,如图,半径为1的⊙M经过直角坐标系的原点O,且与x轴、y轴分别交于点A、B,点A的坐标为(,0),⊙M的切线OC与直线AB交于点C.则∠ACO=
度.
15.(3分)如图,已知点A(2,0),B(0,4),C(2,4),D(6,6),连接AB,CD,将线段AB绕着某一点旋转一定角度,使其与线段CD重合(点A与点C重合,点B与点D重合),则这个旋转中心的坐标为
.
16.(3分)(1)如图1,点D在△ABC的边BC上,若BD=2,CD=3,则S△ABD:S△ACD=
.
(2)如图2,矩形ABCD,点E,F,G,H分别为AB,CD,AD,BC上的点,且EF∥AD,GH∥AB,写出四个矩形S1,S2,S3,S4之间的关系
.
(3)如图3,矩形ABCD,点E在BCD上,点F在CD上,若S△ABE=2,S△CEF=3,S△ADF=4,则矩形ABCD的面积为
.
三、解答题(第17题6分,第18、19题各8分,共22分)
17.(6分)计算:(π﹣4)0+|3﹣tan60°|﹣()﹣2+.
18.(8分)某单位食堂为全体960名职工提供了A,B,C,D四种套餐,为了解职工对这四种套餐的喜好情况.单位随机抽取240名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问卷调查.根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
(1)在抽取的240人中最喜欢A套餐的人数为
.
(2)扇形统计图中“B”占m%,则m=
.
(3)扇形统计图中“C”对应扇形的圆心角的大小为
.
(4)依据本次调查的结果,估计全体960名职工中最喜欢D套餐的人数.
19.(8分)某单位食堂为全体职工提供了套餐服务,“食品安全监督员”准备在甲、乙、丙、丁四名职工中选出.
(1)若只有1人担任“食品安全监督员”,则甲被选中的概率为
.
(2)若有2人担任“食品安全监督员”,求甲被选中的概率.
四、解答题(共2小题,满分16分)
20.(8分)如图,点D,E分别是△ABC的边AB,AC的中点,连接BE,过点C作CF∥BE,交DE的延长线于点F,若EF=3,求DE的长.
21.(8分)为推进垃圾分类,推动绿色发展.某化工厂要购进甲、乙两种型号机器人来进行垃圾分类.用360万元购买甲型机器人和用480万元购买乙型机器人的台数相同,两种型号机器人的单价和为140万元,求设甲型机器人单价.
五、(本题10分)
22.(10分)如图,⊙O是△ABC的外接圆,∠ABC=45°,OC∥AD,AD交BC的延长线于D,AB交OC于E.
(1)求证:AD是⊙O的切线;
(2)若AE=2,CE=2.求⊙O的半径和线段BE的长.
六、解答题(共1小题,满分10分)
23.(10分)如图,已知AB为⊙O的直径,AB=12,点C和点D是⊙O上关于直线AB对称的两个点,连接OC、AC.且∠BOC<90°.直线BC和直线AD相交于点E,过点C作直线CG与线段AB的延长线相交于点F,与直线AD相交于点G.且∠GAF=∠GCE.
(1)求证:直线CG为⊙O的切线;
(2)若点H为线段OB上一点,迄接CH,满足CB=CH,求OH+HC的最大值.
七、(本题12分)
24.(12分)(1)如图1,等腰直角△ABC,∠B=90°,点D为AC的中点,点E为边AB上的一点,作DE垂直DF交BC于点F,求证:DE=DF.
(2)如图2,等腰直角△ABC,∠B=90°,点D为AC的中点,点E为边AB上的一点,线段DE绕着点D逆时针旋转90°得到线段DF,求证:点F在线段BC上;
(3)如图3,直角△ABC,点D为AC的中点,点E为边AB上的一点,线段DE绕着点D逆时针旋转90°得到线段DF,若AB=6,BC=8,
①直接写出线段EF=时,BE的长;
②直接写出△ACF是等腰三角形时,BE的长;
③直接写出△BEF面积的最大值.
八、(本题12分)
25.(12分)已知抛物线y=ax2+bx+6(a≠0)交x轴于点A(6,0)和点B(﹣1,0),交y轴于点C.
(1)求抛物线的解析式和顶点坐标;
(2)如图(1),点P是抛物线上位于直线AC上方的动点,过点P分别作x轴、y轴的平行线,交直线AC于点D,E,当PD+PE取最大值时,求点P的坐标;
(3)如图(2),点M为抛物线对称轴l上一点,点N为抛物线上一点,当直线AC垂直平分△AMN的边MN时,求点N的坐标.
2020-2021学年辽宁省沈阳市皇姑区虹桥中学九年级(下)月考数学试卷(3月份)(五四学制)
参考答案与试题解析
一、选择(每题2分,共20分)
1.下列各数是无理数的是( )
A.0
B.﹣1
C.
D.
【分析】根据无理数是无限不循环小数,可得答案.
【解答】解:0,﹣1,是有理数,是无理数,
故选:C.
2.下列计算正确的是( )
A.a2+2a2=3a4
B.a6÷a3=a2
C.(a﹣b)2=a2﹣b2
D.(ab)2=a2b2
【分析】根据合并同类项法则、同底数幂的乘除法、幂的乘方积的乘方以及完全平方公式进行计算即可.
【解答】解:a2+2a2=3a2,因此选项A不符合题意;
a6÷a3=a6﹣3=a3,因此选项B不符合题意;
(a﹣b)2=a2﹣2ab+b2,因此选项C不符合题意;
(ab)2=a2b2,因此选项D符合题意;
故选:D.
3.如果将一组数据中的每个数都减去5,那么所得的一组新数据( )
A.众数改变,方差改变
B.众数不变,平均数改变
C.中位数改变,方差不变
D.中位数不变,平均数不变
【分析】由每个数都减去5,那么所得的一组新数据的众数、中位数、平均数都减少5,方差不变,据此可得答案.
【解答】解:如果将一组数据中的每个数都减去5,那么所得的一组新数据的众数、中位数、平均数都减少5,方差不变,
故选:C.
4.在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数最有可能是( )
A.5
B.10
C.12
D.15
【分析】设袋子中红球有x个,根据摸出红球的频率稳定在0.25左右列出关于x的方程,求出x的值,从而得出答案.
【解答】解:设袋子中红球有x个,
根据题意,得:=0.25,
解得x=5,
∴袋子中红球的个数最有可能是5个,
故选:A.
5.已知一组数据:3,4,6,7,8,8,下列说法正确的是( )
A.众数是2
B.众数是8
C.中位数是6
D.中位数是7
【分析】根据众数和中位数的定义求解.
【解答】解:数据:3,4,6,7,8,8的众数为8,中为数为6.5.
故选:B.
6.无理数3﹣3在( )
A.3和4之间
B.4和5之间
C.5和6之间
D.6和7之间
【分析】先估算出3的范围,再估算3﹣3的值.
【解答】解:,
∵81<99<100,
∴,
∴,
故无理数3﹣3在6和7之间.
故选:D.
7.四边形ABCD的对角线AC、BD互相平分,要使它成为矩形,需要添加的条件是( )
A.AB=CD
B.AC=BD
C.AB=BC
D.AC⊥BD
【分析】由平行四边形的判定方法得出四边形ABCD是平行四边形,再由矩形的判定方法即可得出结论.
【解答】解:需要添加的条件是AC=BD;理由如下:
∵四边形ABCD的对角线AC、BD互相平分,
∴四边形ABCD是平行四边形,
∵AC=BD,
∴四边形ABCD是矩形(对角线相等的平行四边形是矩形);
故选:B.
8.已知扇形的半径为12,圆心角为60°,则这个扇形的弧长为( )
A.9π
B.6π
C.3π
D.4π
【分析】把扇形的圆心角为和半径为代入弧长公式计算即可.
【解答】解:依题意,n=60,r=12,
∴扇形的弧长===4π.
故选:D.
9.如图,△ABC外接圆⊙O的半径长为6,若∠A=45°.则阴影部分的面积为( )
A.9π﹣18
B.9π
C.6π
D.18π﹣18
【分析】由∠A=45°得出∠BOC=90°,再分别算出三角形OBC与扇形OBC的面积作差求解.
【解答】解:∵∠A=45°,
∴∠BOC=2∠A=90°,
∵⊙O的半径长为6,
∴S△BOC=OC?OB=18.
又∵S扇形OBC==9π,
∴阴影部分的面积为S扇形OBC﹣S△BOC=9π﹣18.
故选:A.
10.如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=30°,则∠C的度数是( )
A.70°
B.45°
C.30°
D.20°
【分析】由BC是⊙O的切线,OB是⊙O的半径,得到∠OBC=90°,根据等腰三角形的性质得到∠A=∠ABO=30°,由外角的性质得到∠BOC=60°,即可求得∠C=30°.
【解答】解:∵BC是⊙O的切线,OB是⊙O的半径,
∴∠OBC=90°,
∵OA=OB,
∴∠A=∠ABO=30°,
∴∠BOC=60°,
∴∠C=30°.
故选:C.
二、填空(每题3分,共18分)
11.(3分)关于x的一元二次方程(m﹣1)x2+2x﹣1=0有两个不相等的实数根,则m的取值范围是 m>0且m≠1 .
【分析】根据一元二次方程的定义和判别式的意义得到m﹣1≠0且△=22﹣4(m﹣1)×(﹣1)>0,然后求出两个不等式的公共部分即可.
【解答】解:根据题意得m﹣1≠0且△=22﹣4(m﹣1)×(﹣1)>0,
解得m>0且m≠1.
故答案为:m>0且m≠1.
12.(3分)若分式方程有增根,则实数a的值是 4或8 .
【分析】对分式方程+=进行正常求解,化简为2x=a﹣4,当x=0或x=2时,分式方程有增根,在x=0和x=2时,分别求出a的值即可.
【解答】解:∵+=,
∴+=,
当x2﹣2x≠0时,
原式化为3x﹣a+x=2x﹣4,
∴2x=a﹣4,
∵分式方程有增根,
∴x=0或x=2,
当x=0时,a=4;
当x=2时,a=8.
故答案是4或8.
13.(3分)如图,在圆内接正六边形ABCDEF中,半径OC=4,OG⊥BC,垂足为点G,则正六边形的中心角= 60° ,边长= 4 ,边心距= 2 .
【分析】由正六边形的性质得∠COD==60°,再证△OCD是等边三角形,得BC=CD=OC=4,再由垂径定理和含30°角的直角三角形的性质求出OG即可.
【解答】解:在圆内接正六边形ABCDEF中,∠COD==60°,
∵OC=OD,
∴△OCD是等边三角形,
∴BC=CD=OC=4,
∵OG⊥BC,
∴CG=BC=2,
∵∠COG=∠COD=30°,
∴OG=CG=2,
故答案为:60°,4,2.
14.(3分)已知,如图,半径为1的⊙M经过直角坐标系的原点O,且与x轴、y轴分别交于点A、B,点A的坐标为(,0),⊙M的切线OC与直线AB交于点C.则∠ACO= 30 度.
【分析】在Rt△AOB中,已知了直径AB和OA的长,即可求得∠OAB、∠OBA的度数;而由弦切角定理知∠OAB=∠BOC,进而可由三角形的外角性质求出∠ACO的度数.
【解答】解:∵AB=2,OA=,
∴cos∠BAO==,
∴∠OAB=30°,∠OBA=60°;
∵OC是⊙M的切线,
∴∠BOC=∠BAO=30°,
∴∠ACO=∠OBA﹣∠BOC=30°.
故答案为:30.
15.(3分)如图,已知点A(2,0),B(0,4),C(2,4),D(6,6),连接AB,CD,将线段AB绕着某一点旋转一定角度,使其与线段CD重合(点A与点C重合,点B与点D重合),则这个旋转中心的坐标为 (4,2) .
【分析】画出平面直角坐标系,作出线段AC,BD的垂直平分线的交点P,点P即为旋转中心.
【解答】解:平面直角坐标系如图所示,旋转中心是P点,P(4,2).
故答案为(4,2).
16.(3分)(1)如图1,点D在△ABC的边BC上,若BD=2,CD=3,则S△ABD:S△ACD= 2:3 .
(2)如图2,矩形ABCD,点E,F,G,H分别为AB,CD,AD,BC上的点,且EF∥AD,GH∥AB,写出四个矩形S1,S2,S3,S4之间的关系 = .
(3)如图3,矩形ABCD,点E在BCD上,点F在CD上,若S△ABE=2,S△CEF=3,S△ADF=4,则矩形ABCD的面积为 16 .
【分析】(1)由S△ABD:S△ACD=BD:CD作答.
(2)分别表示出用线段乘积表示S1,S2,S3,S4,然后作比求解.
(3)设BC=AD=x,AB=CD=y,用含xy代数式表示S△ABE,S△CEF,S△ADF与矩形面积解方程求解.
【解答】解:(1)△ABD与△ACD为同高三角形,设高为h,
∴S△ABD:S△ACD=BD?h:CD?h=BD:CD=2:3.
故答案为:2:3.
(2)∵S1=EM?GM,S2=MF?GM,S3=EM?MF,S4=MH?MF,
∴=,=,
∴=.
故答案为:=.
(3)设BC=AD=x,AB=CD=y,
∵S△ABE=2,S△CEF=3,S△ADF=4,
∴DF?x=8,BE?y=4,
∴(x﹣BE)(y﹣DF)=6,即xy﹣BE?y﹣DF?x+DF?BE=6,
将DF?x=8,BE?y=4代入可得xy+DF?BE=18①,
由①得DF?BE=18﹣xy②,
∵DF?x?BE?y=32③,
将②代入③可得(18﹣xy)?xy=32,
解得xy=16或xy=2(舍).
故答案为:16.
三、解答题(第17题6分,第18、19题各8分,共22分)
17.(6分)计算:(π﹣4)0+|3﹣tan60°|﹣()﹣2+.
【分析】直接利用零指数幂的性质以及负指数幂的性质和特殊角的三角函数值以及二次根式的性质分别化简得出答案.
【解答】解:(π﹣4)0+|3﹣tan60°|﹣()﹣2+
=1+3﹣﹣4+3
=2.
18.(8分)某单位食堂为全体960名职工提供了A,B,C,D四种套餐,为了解职工对这四种套餐的喜好情况.单位随机抽取240名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问卷调查.根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
(1)在抽取的240人中最喜欢A套餐的人数为 60 .
(2)扇形统计图中“B”占m%,则m= 35 .
(3)扇形统计图中“C”对应扇形的圆心角的大小为 108° .
(4)依据本次调查的结果,估计全体960名职工中最喜欢D套餐的人数.
【分析】(1)用被调查的职工人数乘以最喜欢A套餐人数所占百分比即可得其人数;
(2)用B套餐的人数除以总人数,即可得出m的值;
(3)先求出C对应人数,继而用360°乘以最喜欢C套餐人数所占比例即可得;
(4)用总人数乘以样本中最喜欢D套餐的人数所占比例即可得.
【解答】解:(1)在抽取的240人中最喜欢A套餐的人数为240×25%=60(人).
故答案为:60;
(2)m%=×100%=35%,即m=35.
故答案为:35;
(3)最喜欢C套餐的人数为240﹣(60+84+24)=72(人),
则扇形统计图中“C”对应扇形的圆心角的大小为360°×=108°,
故答案为:108°;
(4)根据题意得:
960×=96(人),
答:全体960名职工中最喜欢D套餐的人数有96人.
19.(8分)某单位食堂为全体职工提供了套餐服务,“食品安全监督员”准备在甲、乙、丙、丁四名职工中选出.
(1)若只有1人担任“食品安全监督员”,则甲被选中的概率为 .
(2)若有2人担任“食品安全监督员”,求甲被选中的概率.
【分析】(1)直接利用概率公式列式求解即可;
(2)列举出所有结果,利用概率公式列式求解即可.
【解答】解:∵共甲、乙、丙、丁四名职工,
∴甲被选中担任“食品安全监督员”的概率为,
故答案为:;
(2)若有2人担任“食品安全监督员”,则可能会出现的结果为甲乙、甲丙,甲丁,乙丙,乙丁,丙丁共六种结果,选中甲的有3中可能,
∴若有2人担任“食品安全监督员”,求甲被选中的概率=.
四、解答题(共2小题,满分16分)
20.(8分)如图,点D,E分别是△ABC的边AB,AC的中点,连接BE,过点C作CF∥BE,交DE的延长线于点F,若EF=3,求DE的长.
【分析】先证明DE为△ABC的中位线,得到四边形BCFE为平行四边形,求出BC=EF=3,根据中位线定理即可求解.
【解答】解:∵D、E分别是△ABC的边AB、AC的中点,
∴DE为△ABC的中位线,
∴DE∥BC,DE=BC,
∴EF∥BC,
∵CF∥BE,
∴四边形BCFE为平行四边形,
∴BC=EF=3,
∴DE=BC=.
21.(8分)为推进垃圾分类,推动绿色发展.某化工厂要购进甲、乙两种型号机器人来进行垃圾分类.用360万元购买甲型机器人和用480万元购买乙型机器人的台数相同,两种型号机器人的单价和为140万元,求设甲型机器人单价.
【分析】设甲种型号机器人每台的价格是x万元,根据“用360万元购买甲型机器人和用480万元购买乙型机器人的台数相同”,列出关于x的分式方程.
【解答】解:设甲型机器人每台x万元,
根据题意,可得:,
解得:x=60,
经检验,x=60是原分式方程的解,且符合题意,
答:甲型机器人每台60万元.
五、(本题10分)
22.(10分)如图,⊙O是△ABC的外接圆,∠ABC=45°,OC∥AD,AD交BC的延长线于D,AB交OC于E.
(1)求证:AD是⊙O的切线;
(2)若AE=2,CE=2.求⊙O的半径和线段BE的长.
【分析】(1)连接OA,根据切线的性质得到OA⊥AD,再根据圆周角定理得到∠AOC=2∠ABC=90°,然后根据平行线的判定即可得到结论;
(2)设⊙O的半径为R,则OA=R,OE=R﹣2,AE=2,在Rt△OAE中根据勾股定理可计算出R=4;设⊙O的半径为R,延长CO交⊙O于F,连接AF,GJ
相似三角形的性质即可得到结论.
【解答】(1)证明:连接OA,如图,
∵AD是⊙O的切线,
∴OA⊥AD,
∵∠AOC=2∠ABC=2×45°=90°,
∴OA⊥OC,
∴AD∥OC,
∴OA⊥AD,
∴AD是⊙O的切线
(2)解:设⊙O的半径为R,则OA=R,OE=R﹣2,AE=2,
在Rt△OAE中,∵AO2+OE2=AE2,
∴R2+(R﹣2)2=(2)2,解得R=1,(负值舍去),
延长CO交⊙O于F,连接AF,
则△CEB∽△AEF,
∴,
∵EF=2R﹣2=2,
∴BE=.
六、解答题(共1小题,满分10分)
23.(10分)如图,已知AB为⊙O的直径,AB=12,点C和点D是⊙O上关于直线AB对称的两个点,连接OC、AC.且∠BOC<90°.直线BC和直线AD相交于点E,过点C作直线CG与线段AB的延长线相交于点F,与直线AD相交于点G.且∠GAF=∠GCE.
(1)求证:直线CG为⊙O的切线;
(2)若点H为线段OB上一点,迄接CH,满足CB=CH,求OH+HC的最大值.
【分析】(1)由题意可知:∠CAB=∠GAF,由圆的性质可知:∠CAB=∠OCA,所以∠OCA=∠GCE,从而可证明直线CG是⊙O的切线;
(2)由于CB=CH,所以∠CBH=∠CHB,易证∠CBH=∠OCB,从而可证明△CBH∽△OBC,可得=,所以HB=,由于BC=HC,所以OH+HC=6﹣+BC,利用二次函数的性质即可求出OH+HC的最大值.
【解答】解:(1)由题意可知:∠CAB=∠GAF,
∵AB是⊙O的直径,
∴∠ACB=90°
∵OA=OC,
∴∠CAB=∠OCA,
∴∠OCA+∠OCB=90°,
∵∠GAF=∠GCE,
∴∠GCE+∠OCB=∠OCA+∠OCB=90°,
∵OC是⊙O的半径,
∴直线CG是⊙O的切线.
(2)∵CB=CH,
∴∠CBH=∠CHB,
∵OB=OC,
∴∠CBH=∠OCB,
∴△CBH∽△OBC,
∴=,
∵AB=12,
∴BC2=HB?OC=6HB,
∴HB=,
∴OH=OB﹣HB=6﹣,
∵CB=CH,
∴OH+HC=6﹣+BC,
当∠BOC=90°,
此时BC=6,
∵∠BOC<90°,
∴0<BC<6,
令BC=x,
∴OH+HC=﹣(x﹣3)2+,
当x=3时,
∴OH+HC可取得最大值,最大值为.
七、(本题12分)
24.(12分)(1)如图1,等腰直角△ABC,∠B=90°,点D为AC的中点,点E为边AB上的一点,作DE垂直DF交BC于点F,求证:DE=DF.
(2)如图2,等腰直角△ABC,∠B=90°,点D为AC的中点,点E为边AB上的一点,线段DE绕着点D逆时针旋转90°得到线段DF,求证:点F在线段BC上;
(3)如图3,直角△ABC,点D为AC的中点,点E为边AB上的一点,线段DE绕着点D逆时针旋转90°得到线段DF,若AB=6,BC=8,
①直接写出线段EF=时,BE的长;
②直接写出△ACF是等腰三角形时,BE的长;
③直接写出△BEF面积的最大值.
【分析】(1)证明:如图1中,连接BD.证明△EDB≌△FDC(ASA),可得结论.
(2)如图2中,连接DB,CF.证明△EDB≌△FDC(SAS),推出∠DBE=∠DCF=45°,推出点F在线段BC上.
(3)①如图3﹣1中,过点D作DT⊥AB于T.解直角三角形求出ET可得结论.
②证明△AFC是等腰直角三角形,推出点E与A重合,可得结论.
③如图3﹣3中,过点D作DT⊥AB于T,过点F作FR⊥DT于R.证明△DTE≌△FRD(AAS),推出ET=DR,DT=FR=4,设ET=DR=m,则RT=4﹣m,构建二次函数,可得结论.
【解答】(1)证明:如图1中,连接BD.
∵△ABC是等腰直角三角形,AD=DC,
∴BD⊥AC,BD=DA=DC,
∴BD⊥AC,
∵ED⊥DF,
∴∠EDF=∠BDC=90°,
∴∠EDB=∠FDC,
∵∠DBE=∠C=45°,
∴△EDB≌△FDC(ASA),
∴DE=DF.
(2)证明:如图2中,连接DB,CF.
∵∠BDC=∠EDF=90°,
∴∠BDE=∠CDF,
∵DB=DC,DE=DF,
∴△EDB≌△FDC(SAS),
∴∠DBE=∠DCF=45°,
∴点F在线段BC上.
(3)①如图3﹣1中,过点D作DT⊥AB于T.
∵∠ATD=∠ABC=90°,
∴DT∥CB,
∵AD=DC,
∴AT=TB=3,
∴DT=BC=4,
∵△DEF是等腰直角三角形,EF=,
∴DE=DF=,
∴ET===1,
∴BE=TB+ET=3+1=4,
当点E在点T的下方时,BE=3﹣1=2,
综上所述,满足条件的BE的值为4或2.
②如图3﹣2中,
∵△ACF是等腰三角形,
又∵AD=DC=DF,
∴∠AFC=90°,
∴△AFC是等腰直角三角形,
∴点E与A重合,
∴BE=6.
③如图3﹣3中,过点D作DT⊥AB于T,过点F作FR⊥DT于R.
∵∠DTE=∠FRD=90°,∠EDT=∠DFR,DE=DF,
∴△DTE≌△FRD(AAS),
∴ET=DR,DT=FR=4,
设ET=DR=m,则RT=4﹣m,
∴S△EFB=(3+m)(4﹣m)=(﹣m2+m+12)=﹣(m﹣)2+,
∵﹣<0,
∴△BEF的面积有最大值,最大值为.
八、(本题12分)
25.(12分)已知抛物线y=ax2+bx+6(a≠0)交x轴于点A(6,0)和点B(﹣1,0),交y轴于点C.
(1)求抛物线的解析式和顶点坐标;
(2)如图(1),点P是抛物线上位于直线AC上方的动点,过点P分别作x轴、y轴的平行线,交直线AC于点D,E,当PD+PE取最大值时,求点P的坐标;
(3)如图(2),点M为抛物线对称轴l上一点,点N为抛物线上一点,当直线AC垂直平分△AMN的边MN时,求点N的坐标.
【分析】(1)将点A,B坐标代入抛物线解析式中,解方程组即可得出结论;
(2)先求出OA=OC=6,进而得出∠OAC=45°,进而判断出PD=PE,即可得出当PE的长度最大时,PE+PD取最大值,设出点E坐标,表示出点P坐标,建立PE=﹣t2+6t=﹣(t﹣3)2+9,即可得出结论;
(3)先判断出NF∥x轴,进而求出点N的纵坐标,即可建立方程求解得出结论.
【解答】解:(1)∵抛物线y=ax2+bx+6经过点A(6,0),B(﹣1,0),
∴,
∴,
∴抛物线的解析式为y=﹣x2+5x+6=﹣(x﹣)2+,
∴抛物线的解析式为y=﹣x2+5x+6,顶点坐标为(,);
(2)由(1)知,抛物线的解析式为y=﹣x2+5x+6,
∴C(0,6),
∴OC=6,
∵A(6,0),
∴OA=6,
∴OA=OC,
∴∠OAC=45°,
∵PD平行于x轴,PE平行于y轴,
∴∠DPE=90°,∠PDE=∠DAO=45°,
∴∠PED=45°,
∴∠PDE=∠PED,
∴PD=PE,
∴PD+PE=2PE,
∴当PE的长度最大时,PE+PD取最大值,
∵A(6,0),C(0,6),
∴直线AC的解析式为y=﹣x+6,
设E(t,﹣t+6)(0<t<6),则P(t,﹣t2+5t+6),
∴PE=﹣t2+5t+6﹣(﹣t+6)=﹣t2+6t=﹣(t﹣3)2+9,
当t=3时,PE最大,此时,﹣t2+5t+6=12,
∴P(3,12);
(3)如图(2),设直线AC与抛物线的对称轴l的交点为F,连接NF,
∵点F在线段MN的垂直平分线AC上,
∴FM=FN,∠NFC=∠MFC,
∵l∥y轴,
∴∠MFC=∠OCA=45°,
∴∠MFN=∠NFC+∠MFC=90°,
∴NF∥x轴,
由(2)知,直线AC的解析式为y=﹣x+6,
当x=时,y=,
∴F(,),
∴点N的纵坐标为,
设N的坐标为(m,﹣m2+5m+6),
∴﹣m2+5m+6=,解得,m=或m=,
∴点N的坐标为(,)或(,).
同课章节目录
