2.8 圆锥的侧面积同步练习 -2020——2021学年苏科版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 2.8 圆锥的侧面积同步练习 -2020——2021学年苏科版九年级数学上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 155.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-03 15:43:46 | ||
图片预览



文档简介
2.8
圆锥的侧面积
一、选择题
1.圆锥的底面半径是5
cm,侧面展开图的圆心角是180°,圆锥的高是
( )
A.5
cm
B.10
cm
C.6
cm
D.5
cm
2.如图1,在正方形网格中,扇形OAB是圆锥的侧面展开图,∠AOB=90°,若每个小正方形的边长均为1厘米,则这个圆锥的底面圆半径为( )
图1
A.厘米
B.厘米
C.厘米
D.2厘米
3.[2020·湖北]
一个圆锥的底面圆半径是4
cm,其侧面展开图的圆心角是120°,则圆锥的母线长是
( )
A.8
cm
B.12
cm
C.16
cm
D.24
cm
4.[2020·青海]
如图2是一个废弃的扇形统计图,小明同学利用它的阴影部分制作一个圆锥,则这个圆锥的底面圆半径是
( )
图2
A.3.6
B.1.8
C.3
D.6
5.如图3,要制作一顶圆锥形的烟囱帽,使底面圆的半径与母线长的比是4∶5,那么所需扇形铁皮的圆心角应为
( )
图3
A.288°
B.216°
C.144°
D.120°
6.如图4,蒙古包可近似地看作由圆锥和圆柱组成,若用毛毡搭建一个底面圆面积为25π
m2,圆柱高为3
m,圆锥高为2
m的蒙古包,则需要毛毡的面积是
( )
图4
A.(30+5)π
m2
B.40π
m2
C.(30+5)π
m2
D.55π
m2
7.[2019·宁波]
如图5所示,矩形纸片ABCD中,AD=6
cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB的长为
( )
图5
A.3.5
cm
B.4
cm
C.4.5
cm
D.5
cm
8.[2019·荆州]
如图6,C为扇形OAB的半径OB上一点,将△OAC沿AC折叠,点O恰好落在上的点D处,且∶=1∶3(表示的长),若将此扇形OAB围成一个圆锥,则圆锥的底面圆半径与母线长的比为
( )
图6
A.1∶3
B.1∶π
C.1∶4
D.2∶9
二、填空题
9.[2020·宿迁]
用半径为4,圆心角为90°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆的半径为 .?
10.[2019·徐州]
如图7,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆半径r=2
cm,扇形的圆心角θ=120°,则该圆锥的母线长l为 cm.?
图7
11.[2020·徐州]
如图8,在Rt△ABC中,∠C=90°,AC=4,BC=3.若以AC所在直线为轴,把△ABC旋转一周,得到一个圆锥,则这个圆锥的侧面积等于 .?
图8
12.如图9,现有一张圆心角为108°,半径为40
cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面圆半径为10
cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的圆心角θ为 .?
图9
三、解答题
13.已知扇形的圆心角为120°,面积为300π
cm2.
(1)求扇形的弧长;
(2)如果把这个扇形卷成一个圆锥,那么圆锥的高是多少?
14.[2019·启东期末]
如图10,一个圆锥形工艺品,它的高为3
cm,侧面展开图是半圆.求:
(1)圆锥的母线长与底面圆半径之比;
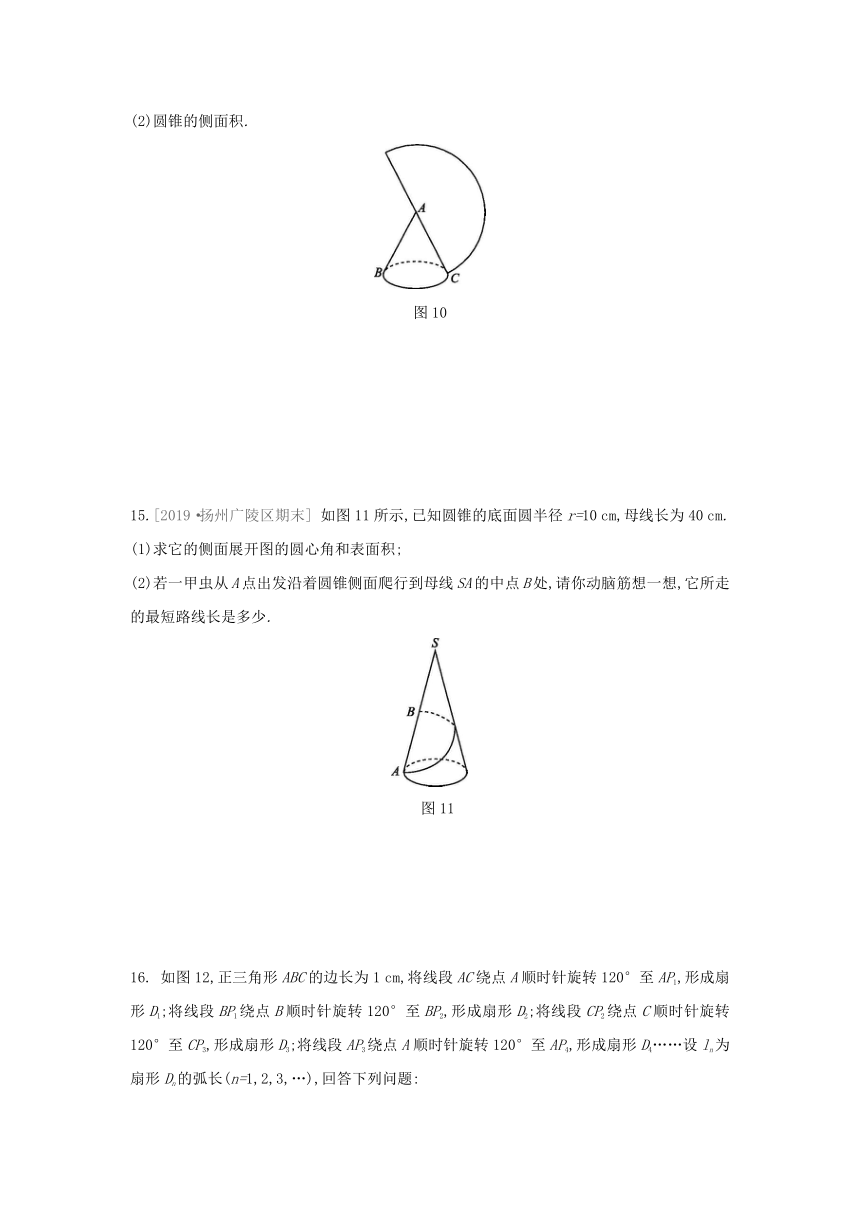
(2)圆锥的侧面积.
图10
15.[2019·扬州广陵区期末]
如图11所示,已知圆锥的底面圆半径r=10
cm,母线长为40
cm.
(1)求它的侧面展开图的圆心角和表面积;
(2)若一甲虫从A点出发沿着圆锥侧面爬行到母线SA的中点B处,请你动脑筋想一想,它所走的最短路线长是多少.
图11
16.
如图12,正三角形ABC的边长为1
cm,将线段AC绕点A顺时针旋转120°至AP1,形成扇形D1;将线段BP1绕点B顺时针旋转120°至BP2,形成扇形D2;将线段CP2绕点C顺时针旋转120°至CP3,形成扇形D3;将线段AP3绕点A顺时针旋转120°至AP4,形成扇形D4……设ln为扇形Dn的弧长(n=1,2,3,…),回答下列问题:
(1)按要求填表:
n
1
2
3
4
ln(cm)
?
?
?
?
(2)根据上表,试估计n至少为何值时,扇形Dn的弧长能绕地球赤道一周?(设地球赤道的半径为6400
km)
(3)圆锥的侧面积实际上是侧面展开图的 .若已知圆锥侧面展开图的圆心角为n°和半径R,则它的侧面积是 ;若已知圆锥的母线长l和底面圆半径r,则它的侧面积是 .?
图12
答案
1.[解析]
A 设圆锥的母线长为R.根据题意,得2π·5=,解得R=10.即圆锥的母线长为10
cm,∴圆锥的高为=5(cm).故选A.
2.[解析]
B 扇形的半径为=2(厘米),∴扇形的弧长为=π(厘米),∴这个圆锥的底面圆半径为π÷2π=(厘米).故选B.
3.[解析]
B 设圆锥的母线长为R
cm.
∵圆锥的底面圆周长为2π×4=8π(cm),
∴=8π,
解得R=12,即圆锥的母线长为12
cm.故选B.
4.[解析]
A 设这个圆锥的底面圆半径为r.
根据题意,得2πr=.
解得r=3.6,
即这个圆锥的底面圆半径是3.6.故选A.
5.[解析]
A ∵底面圆的半径与母线长的比是4∶5,
∴设底面圆的半径为4x,则母线长是5x,扇形铁皮的圆心角为n°,
则2π×4x=,解得n=288.故选A.
6.[解析]
A 设底面圆的半径为R
m,则πR2=25π,解得R=5,则圆锥的母线长为=(m),所以圆锥的侧面积为×2π×5×=5π(m2),圆柱的侧面积为2π×5×3=30π(m2),所以需要毛毡的面积为(30π+5π)m2.故选A.
7.[解析]
B 设AB=x
cm,则DE=(6-x)cm.
根据题意,得=π(6-x),解得x=4.
故选B.
8.[解析]
D 连接OD交AC于点M.
由折叠的性质可得OA=AD,
又OD=OA,
∴OA=AD=OD,∴∠AOM=60°.
∵∶=1∶3,∴∠AOB=80°.
设圆锥的底面圆半径为r,母线长为l,则=2πr,∴r∶l=2∶9.故选D.
9.[答案]
1
[解析]
设这个圆锥的底面圆的半径为r.根据题意,得2πr=,
解得r=1,所以这个圆锥的底面圆的半径为1.
10.[答案]
6
[解析]
圆锥的底面圆周长=2π×2=4π(cm).
设圆锥的母线长为R
cm,则=4π,解得R=6.故答案为6.
11.[答案]
15π
[解析]
由已知,得母线长为5,
∴圆锥的侧面积是πrl=5×3×π=15π.故答案为15π.
12.[答案]
18°
[解析]
设剩下扇形纸片的圆心角为n°,则2π×10=,解得n=90.∵扇形纸片的圆心角是108°,∴剪去的扇形纸片的圆心角为108°-90°=18°.
13.解:(1)设扇形的半径为R(R>0)
cm.
根据题意,得300π=,解得R=30,
所以扇形的弧长为=20π(cm).
(2)设圆锥底面圆的半径为r
cm.
根据题意,得2πr=20π,解得r=10,
所以圆锥的高是=20(cm).
14.解:设圆锥底面圆半径为r
cm,母线长为l
cm.(1)由题意知2πr=πl,∴l∶r=2∶1.
答:圆锥的母线长与底面圆半径之比为2∶1.
(2)由题意知r2+(3)2=l2.
把l=2r代入,解得r1=-3(舍去),r2=3,
∴l=6,∴圆锥的侧面积为πrl=18π(cm2).
15.解:(1)设圆锥的侧面展开图的圆心角为n°.=2π×10,解得n=90,故它的侧面展开图的圆心角为90°.
圆锥的表面积为π×102+π×10×40=500π(cm2).
(2)如图,由圆锥的侧面展开图可知,甲虫从A点出发沿着圆锥侧面绕行到母线SA的中点B所走的最短路线长是线段AB的长.
在Rt△ASB中,SA=40
cm,SB=20
cm,
∴AB=20
cm.
∴甲虫所走的最短路线长是20
cm.
12.解:(1)根据弧长公式,得l1==(cm);
l2==(cm);
l3==2π(cm);
l4==(cm).
故填表如下:
n
1
2
3
4
ln(cm)
2π
(2)根据上述规律可知:ln==2π×6400×105,解得n=1.92×109.
(3)面积 πrl
圆锥的侧面积
一、选择题
1.圆锥的底面半径是5
cm,侧面展开图的圆心角是180°,圆锥的高是
( )
A.5
cm
B.10
cm
C.6
cm
D.5
cm
2.如图1,在正方形网格中,扇形OAB是圆锥的侧面展开图,∠AOB=90°,若每个小正方形的边长均为1厘米,则这个圆锥的底面圆半径为( )
图1
A.厘米
B.厘米
C.厘米
D.2厘米
3.[2020·湖北]
一个圆锥的底面圆半径是4
cm,其侧面展开图的圆心角是120°,则圆锥的母线长是
( )
A.8
cm
B.12
cm
C.16
cm
D.24
cm
4.[2020·青海]
如图2是一个废弃的扇形统计图,小明同学利用它的阴影部分制作一个圆锥,则这个圆锥的底面圆半径是
( )
图2
A.3.6
B.1.8
C.3
D.6
5.如图3,要制作一顶圆锥形的烟囱帽,使底面圆的半径与母线长的比是4∶5,那么所需扇形铁皮的圆心角应为
( )
图3
A.288°
B.216°
C.144°
D.120°
6.如图4,蒙古包可近似地看作由圆锥和圆柱组成,若用毛毡搭建一个底面圆面积为25π
m2,圆柱高为3
m,圆锥高为2
m的蒙古包,则需要毛毡的面积是
( )
图4
A.(30+5)π
m2
B.40π
m2
C.(30+5)π
m2
D.55π
m2
7.[2019·宁波]
如图5所示,矩形纸片ABCD中,AD=6
cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AB的长为
( )
图5
A.3.5
cm
B.4
cm
C.4.5
cm
D.5
cm
8.[2019·荆州]
如图6,C为扇形OAB的半径OB上一点,将△OAC沿AC折叠,点O恰好落在上的点D处,且∶=1∶3(表示的长),若将此扇形OAB围成一个圆锥,则圆锥的底面圆半径与母线长的比为
( )
图6
A.1∶3
B.1∶π
C.1∶4
D.2∶9
二、填空题
9.[2020·宿迁]
用半径为4,圆心角为90°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆的半径为 .?
10.[2019·徐州]
如图7,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆半径r=2
cm,扇形的圆心角θ=120°,则该圆锥的母线长l为 cm.?
图7
11.[2020·徐州]
如图8,在Rt△ABC中,∠C=90°,AC=4,BC=3.若以AC所在直线为轴,把△ABC旋转一周,得到一个圆锥,则这个圆锥的侧面积等于 .?
图8
12.如图9,现有一张圆心角为108°,半径为40
cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面圆半径为10
cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的圆心角θ为 .?
图9
三、解答题
13.已知扇形的圆心角为120°,面积为300π
cm2.
(1)求扇形的弧长;
(2)如果把这个扇形卷成一个圆锥,那么圆锥的高是多少?
14.[2019·启东期末]
如图10,一个圆锥形工艺品,它的高为3
cm,侧面展开图是半圆.求:
(1)圆锥的母线长与底面圆半径之比;
(2)圆锥的侧面积.
图10
15.[2019·扬州广陵区期末]
如图11所示,已知圆锥的底面圆半径r=10
cm,母线长为40
cm.
(1)求它的侧面展开图的圆心角和表面积;
(2)若一甲虫从A点出发沿着圆锥侧面爬行到母线SA的中点B处,请你动脑筋想一想,它所走的最短路线长是多少.
图11
16.
如图12,正三角形ABC的边长为1
cm,将线段AC绕点A顺时针旋转120°至AP1,形成扇形D1;将线段BP1绕点B顺时针旋转120°至BP2,形成扇形D2;将线段CP2绕点C顺时针旋转120°至CP3,形成扇形D3;将线段AP3绕点A顺时针旋转120°至AP4,形成扇形D4……设ln为扇形Dn的弧长(n=1,2,3,…),回答下列问题:
(1)按要求填表:
n
1
2
3
4
ln(cm)
?
?
?
?
(2)根据上表,试估计n至少为何值时,扇形Dn的弧长能绕地球赤道一周?(设地球赤道的半径为6400
km)
(3)圆锥的侧面积实际上是侧面展开图的 .若已知圆锥侧面展开图的圆心角为n°和半径R,则它的侧面积是 ;若已知圆锥的母线长l和底面圆半径r,则它的侧面积是 .?
图12
答案
1.[解析]
A 设圆锥的母线长为R.根据题意,得2π·5=,解得R=10.即圆锥的母线长为10
cm,∴圆锥的高为=5(cm).故选A.
2.[解析]
B 扇形的半径为=2(厘米),∴扇形的弧长为=π(厘米),∴这个圆锥的底面圆半径为π÷2π=(厘米).故选B.
3.[解析]
B 设圆锥的母线长为R
cm.
∵圆锥的底面圆周长为2π×4=8π(cm),
∴=8π,
解得R=12,即圆锥的母线长为12
cm.故选B.
4.[解析]
A 设这个圆锥的底面圆半径为r.
根据题意,得2πr=.
解得r=3.6,
即这个圆锥的底面圆半径是3.6.故选A.
5.[解析]
A ∵底面圆的半径与母线长的比是4∶5,
∴设底面圆的半径为4x,则母线长是5x,扇形铁皮的圆心角为n°,
则2π×4x=,解得n=288.故选A.
6.[解析]
A 设底面圆的半径为R
m,则πR2=25π,解得R=5,则圆锥的母线长为=(m),所以圆锥的侧面积为×2π×5×=5π(m2),圆柱的侧面积为2π×5×3=30π(m2),所以需要毛毡的面积为(30π+5π)m2.故选A.
7.[解析]
B 设AB=x
cm,则DE=(6-x)cm.
根据题意,得=π(6-x),解得x=4.
故选B.
8.[解析]
D 连接OD交AC于点M.
由折叠的性质可得OA=AD,
又OD=OA,
∴OA=AD=OD,∴∠AOM=60°.
∵∶=1∶3,∴∠AOB=80°.
设圆锥的底面圆半径为r,母线长为l,则=2πr,∴r∶l=2∶9.故选D.
9.[答案]
1
[解析]
设这个圆锥的底面圆的半径为r.根据题意,得2πr=,
解得r=1,所以这个圆锥的底面圆的半径为1.
10.[答案]
6
[解析]
圆锥的底面圆周长=2π×2=4π(cm).
设圆锥的母线长为R
cm,则=4π,解得R=6.故答案为6.
11.[答案]
15π
[解析]
由已知,得母线长为5,
∴圆锥的侧面积是πrl=5×3×π=15π.故答案为15π.
12.[答案]
18°
[解析]
设剩下扇形纸片的圆心角为n°,则2π×10=,解得n=90.∵扇形纸片的圆心角是108°,∴剪去的扇形纸片的圆心角为108°-90°=18°.
13.解:(1)设扇形的半径为R(R>0)
cm.
根据题意,得300π=,解得R=30,
所以扇形的弧长为=20π(cm).
(2)设圆锥底面圆的半径为r
cm.
根据题意,得2πr=20π,解得r=10,
所以圆锥的高是=20(cm).
14.解:设圆锥底面圆半径为r
cm,母线长为l
cm.(1)由题意知2πr=πl,∴l∶r=2∶1.
答:圆锥的母线长与底面圆半径之比为2∶1.
(2)由题意知r2+(3)2=l2.
把l=2r代入,解得r1=-3(舍去),r2=3,
∴l=6,∴圆锥的侧面积为πrl=18π(cm2).
15.解:(1)设圆锥的侧面展开图的圆心角为n°.=2π×10,解得n=90,故它的侧面展开图的圆心角为90°.
圆锥的表面积为π×102+π×10×40=500π(cm2).
(2)如图,由圆锥的侧面展开图可知,甲虫从A点出发沿着圆锥侧面绕行到母线SA的中点B所走的最短路线长是线段AB的长.
在Rt△ASB中,SA=40
cm,SB=20
cm,
∴AB=20
cm.
∴甲虫所走的最短路线长是20
cm.
12.解:(1)根据弧长公式,得l1==(cm);
l2==(cm);
l3==2π(cm);
l4==(cm).
故填表如下:
n
1
2
3
4
ln(cm)
2π
(2)根据上述规律可知:ln==2π×6400×105,解得n=1.92×109.
(3)面积 πrl
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
