4.4.5一次函数的应用—分段函数 课件 2020-2021学年湘教版数学八年级下册(28张)
文档属性
| 名称 | 4.4.5一次函数的应用—分段函数 课件 2020-2021学年湘教版数学八年级下册(28张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 923.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-03 00:00:00 | ||
图片预览







文档简介
第四章 一次函数
第1课时 利用一次函数解决实际问题
4.5 一次函数的应用
创设情境,激发兴趣
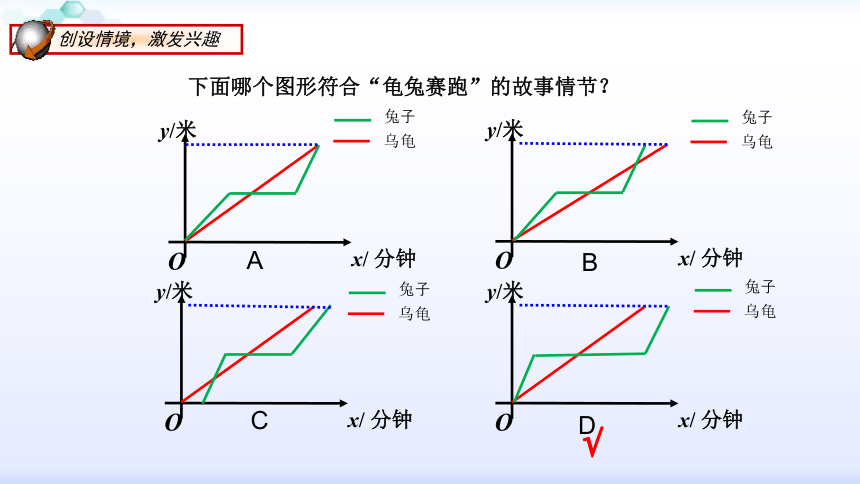
下面哪个图形符合“龟兔赛跑”的故事情节?
A
x/ 分钟
y/米
O
x/ 分钟
y/米
O
x/ 分钟
y/米
O
x/ 分钟
y/米
O
A
D
B
C
兔子
乌龟
兔子
乌龟
兔子
乌龟
兔子
乌龟
√
创设情境,激发兴趣
该图表示的函数是正比例函数吗?是一次函数吗?
x/ 分钟
y/米
O
兔子
5
30
35
100
250
从图中你能获取哪些信息?
创设情境,激发兴趣
某地为保护环境,鼓励节约用电,实行阶梯电价制度.规定每户居民每月用电量不超过160kW·h,则按0.6元/(kW·h)收费;若超过160kW·h,则超出部分每1kW·h加收0.1元.
(1)写出某户居民某月应缴纳的电费y(元)与用电量x(kW·h)之间的函数表达式;
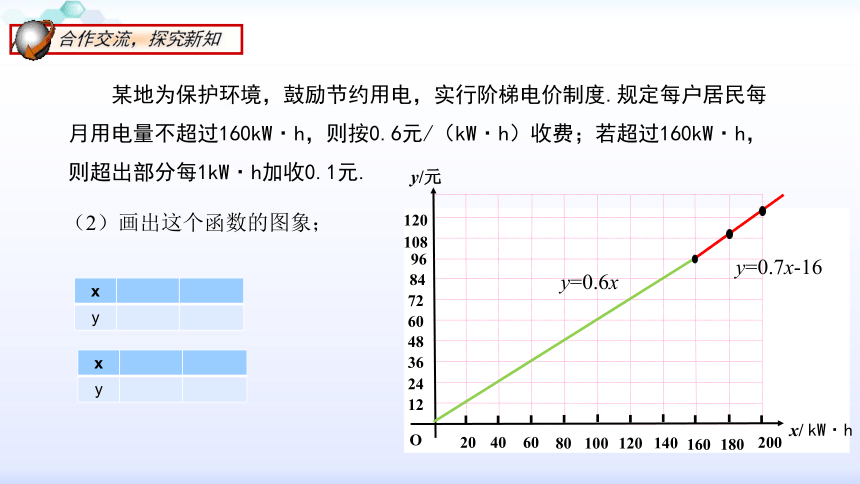
(2)画出这个函数的图象;
(3)小王家3月份,4月份分别用电150kW·h和200kW·h,应缴纳电费各多少元?
合作交流,探究新知
某地为保护环境,鼓励节约用电,实行阶梯电价制度.规定每户居民每月用电量不超过160kW·h,则按0.6元/(kW·h)收费;若超过160kW·h,则超出部分每1kW·h加收0.1元.
(1)写出某户居民某月应缴纳的电费y(元)与用电量x(kW·h)之间的函数表达式;
超出部分每1kW·h加收0.1元是什么意思?
0≤x≤160时,1kW·h缴费 0.6 元;
x>160时,超过的部分1kW·h 缴费(0.6+0.1)元.
电费 = 用电量×电价
合作交流,探究新知
x/ kW·h
y/元
20
40
60
80
100
120
12
48
60
24
36
72
84
96
140
160
180
200
O
108
120
(2)画出这个函数的图象;
y=0.6x
y=0.7x-16
合作交流,探究新知
某地为保护环境,鼓励节约用电,实行阶梯电价制度.规定每户居民每月用电量不超过160kW·h,则按0.6元/(kW·h)收费;若超过160kW·h,则超出部分每1kW·h加收0.1元.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
y
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
y
(3)小王家3月份,4月份分别用电150kW·h和200kW·h,应缴纳电费各多少元?
小王家6月份的缴纳电费为194元,你能算出小王家6月份的用电量为多少吗?
因为194>160×0.6
某地为保护环境,鼓励节约用电,实行阶梯电价制度.规定每户居民每月用电量不超过160kW·h,则按0.6元/(kW·h)收费;若超过160kW·h,则超出部分每1kW·h加收0.1元.
合作交流,探究新知
当y=194时,194=0.7x-16
解得 x=300
即6月份的用电量为300kW·h
在自变量的不同取值范围内,函数关系的表达式有不同的形式,这样的函数称为分段函数,分段函数在生活中也有很多应用.
分段函数
0.6x (0≤x≤160)
0.7x-16 (x>160)
y =
1.信禾公共汽车公司规定:旅客可免费携带一定重量的行李,如果超过规定的重量,则需要购买行李车票,行李费用y(元)与行李重量x(千克)的函数关系如图所示
6
10
80
30
x(千克)
60
y(元)
0
你能通过图象给出的信息知道旅客最多可免费携带多少千克的行李?
解决问题,应用新知
2.某市出租车计费方式如图所示.根据图象信息,下列说法错误的是( )
A. 出租车起步价是10元
B.在3千米内只收起步价
C.超过3千米的部分每千米收3元
D.超过3千米时所需费用y与x之间的函数表达式是y=2x+4
C
解决问题,应用新知
3.某复印店复印收费y(元)与复印面数(8开纸)x(面)的函数图象如图所示,那么从图象中可以看出,复印100面以内,每面收费 元,复印超过100面的部分,每面收费 元
0.4
0.5
解决问题,应用新知
“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,它像乌龟提出挑战。
请根据图像说一说《新龟兔赛跑》的故事。
《新龟兔赛跑》
深入探究,拓展新知
兔子
乌龟
x/ 分钟
y/米
O
起点
终点
50
《新龟兔赛跑》
这一次,兔子先让乌龟先跑若干分钟,然后再开始追赶,结果他们同时到达终点。
兔子
乌龟
起点
终点
x/ 分钟
y/米
O
你能画出函数图像吗?
深入探究,拓展新知
起跑时存在路程差
起跑时存在时间差
图1
图2
起点
终点
兔子
乌龟
x/ 分钟
y/米
O
兔子
乌龟
x/ 分钟
y/米
O
起点
终点
深入探究,拓展新知
【例1】
甲、乙两地相距40km,小明8:00骑自行车由甲地去乙地,平均车速为8km/h;
小红10:00坐公共汽车也由甲地去乙地,平均车速为40km/h.设小明所用的时间为x(h),小明与甲地的距离为y1(km),小红离甲地的距离为y2(km).
(1)分别写出y1,y2与x之间的函数表达式.
(2)在同一个直角坐标系中,画出这两个函数的图象,并指出谁先到达乙地.
深入探究,拓展新知
解(2)
甲、乙两地相距40km,小明8:00点骑自行车由甲地去乙地,平均车速为8km/h;小红10:00坐公共汽车也由甲地去乙地,平均车速为40km/h.设小明所用的时间为x(h),小明与甲地的距离为y1(km),小红离甲地的距离为y2(km).
(2)在同一个直角坐标系中,画出这两个函数的图象,并指出谁先到达乙地.
x/ h
y/km
1
2
3
8
32
40
16
24
4
5
0
小红y2=40(x-2)
(0≤ x ≤5)
(2≤ x ≤3)
小明y1= 8x
y1= 8x
y2=40(x-2)
两个一次函数图像的交点有什么样的实际意义?
深入探究,拓展新知
(2.5,20)
1.某音像店对外出租光盘的收费标准是:每张光盘在出租后头两天的租金为0.8元/天,以后每天收0.5元.求一张光盘在租出后第n天的租金y(元)与时间t(天)之间的函数表达式.
解决问题,应用新知
2.某移动公司对于移动话费推出两种收费方式:
A方案:每月收取基本月租费25元,另收通话费为0.36元/min;
B方案:零月租费,通话费为0.5元/min.
(1)试写出A,B两种方案所付话费y(元)与通话时间t(min)之间的函数表达式;
(2)分别画出这两个函数的图象;
(3)熊老师每月通话300min,我选择哪种付费方式比较合算?
解决问题,应用新知
解(1) A方案:
B方案:
(2)这两个函数的图象如下
●
y = 25+0.36t(t≥0)
●
y = 0.5t(t≥0)
y = 25+0.36t(t≥0)
y = 0.5t (t≥0)
O
5
15
10
5
10
y / 元
t / min
30
15
25
35
A方案
O
1
3
2
1
2
3
y / 元
t / min
B方案
●
3.甲、乙二人骑自行车同时从张庄出发,沿同一路线去李庄.甲行驶20分钟因事耽误一会儿,事后继续按原速行驶.如图表示甲、乙二人骑自行车行驶的路程y(千米)随时间x(分)变化的图象(全程),根据图象回答下列问题:
(1)乙比甲晚多长时间到达李庄?
(2)甲因事耽误了多长时间?
(3)x为何值时,乙行驶的路程比甲行驶
的路程多1千米?
解决问题,应用新知
解决问题,应用新知
解 (3)
当 x=36或48时,乙行驶的路程比甲行驶的路程多1千米
①
3.甲、乙二人骑自行车同时从张庄出发,沿同一路线去李庄.甲行驶20分钟因事耽误一会儿,事后继续按原速行驶.如图表示甲、乙二人骑自行车行驶的路程y(千米)随时间x(分)变化的图象(全程),根据图象回答下列问题:
(3)x为何值时,乙行驶的路程比甲行驶的路程多1千米?
x ? 5 = 1
1
6
②
x ? ( x ? 5)= 1
1
6
1
4
解得x= 36
解得x= 48
y= x - 5
1
4
y= x
1
6
y= 5
归纳总结,深化新知
本节课你有哪些收获?
布置作业,巩固新知
1.“清明节”期间,王老师一家自驾游去了离家170千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
(1)求他们出发半小时时,离家多少千米?
(2)求出AB段图象的函数表达式;
(3)他们出发2小时时,离目的地还有多少千米?
布置作业,巩固新知
2.为响应绿色出行号召,越来越多的市民选择租用共享单车出行.已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式,下图描述了两种方式需支付金额y(元)与骑行时间x(时)之间的函数关系,根据图象回答下列问题:
(1)求手机支付金额y(元)与骑行时间x(时)的函数表达式;
(2)李老师经常骑行共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算?
布置作业,巩固新知
(选做题)3.在“美丽广西,清洁乡村”活动中,李家村村委会提出两种购买垃圾桶的方案.
方案1:买分类垃圾桶,需要费用3000元,以后每月的垃圾处理费用为250元;
方案2:买不分类垃圾桶,需要费用1000元,以后每月的垃圾处理费用为500元.
设方案1的购买费和每月垃圾处理费共为y1元,方案2的购买费和每月垃圾处理费共为y2元,交费时间为x个月.
(1)直接写出y1,y2与x之间的函数表达式(不用写自变量的取值范围);
(2)在同一坐标系中画出函数y1,y2的图象;
(3)在垃圾桶使用寿命相同的情况下,哪种方案省钱?
布置作业,巩固新知
(选做题)4.如图1所示,在A、B两地间有汽车站C站,客车由A地驶向C站,货车由B地驶向A地,两车同时出发,匀速行驶,图2是客车、货车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数关系图象.
(1)填空:A、B两地相距__________千米;
(2)求两小时后,货车离站C的路程y2与行驶时间x之间的函数关系式.
(3)客、货两车何时相遇?
?
谢谢!
-3
O
3
9
6
-3
3
6
9
x
y
第1课时 利用一次函数解决实际问题
4.5 一次函数的应用
创设情境,激发兴趣
下面哪个图形符合“龟兔赛跑”的故事情节?
A
x/ 分钟
y/米
O
x/ 分钟
y/米
O
x/ 分钟
y/米
O
x/ 分钟
y/米
O
A
D
B
C
兔子
乌龟
兔子
乌龟
兔子
乌龟
兔子
乌龟
√
创设情境,激发兴趣
该图表示的函数是正比例函数吗?是一次函数吗?
x/ 分钟
y/米
O
兔子
5
30
35
100
250
从图中你能获取哪些信息?
创设情境,激发兴趣
某地为保护环境,鼓励节约用电,实行阶梯电价制度.规定每户居民每月用电量不超过160kW·h,则按0.6元/(kW·h)收费;若超过160kW·h,则超出部分每1kW·h加收0.1元.
(1)写出某户居民某月应缴纳的电费y(元)与用电量x(kW·h)之间的函数表达式;
(2)画出这个函数的图象;
(3)小王家3月份,4月份分别用电150kW·h和200kW·h,应缴纳电费各多少元?
合作交流,探究新知
某地为保护环境,鼓励节约用电,实行阶梯电价制度.规定每户居民每月用电量不超过160kW·h,则按0.6元/(kW·h)收费;若超过160kW·h,则超出部分每1kW·h加收0.1元.
(1)写出某户居民某月应缴纳的电费y(元)与用电量x(kW·h)之间的函数表达式;
超出部分每1kW·h加收0.1元是什么意思?
0≤x≤160时,1kW·h缴费 0.6 元;
x>160时,超过的部分1kW·h 缴费(0.6+0.1)元.
电费 = 用电量×电价
合作交流,探究新知
x/ kW·h
y/元
20
40
60
80
100
120
12
48
60
24
36
72
84
96
140
160
180
200
O
108
120
(2)画出这个函数的图象;
y=0.6x
y=0.7x-16
合作交流,探究新知
某地为保护环境,鼓励节约用电,实行阶梯电价制度.规定每户居民每月用电量不超过160kW·h,则按0.6元/(kW·h)收费;若超过160kW·h,则超出部分每1kW·h加收0.1元.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
y
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
y
(3)小王家3月份,4月份分别用电150kW·h和200kW·h,应缴纳电费各多少元?
小王家6月份的缴纳电费为194元,你能算出小王家6月份的用电量为多少吗?
因为194>160×0.6
某地为保护环境,鼓励节约用电,实行阶梯电价制度.规定每户居民每月用电量不超过160kW·h,则按0.6元/(kW·h)收费;若超过160kW·h,则超出部分每1kW·h加收0.1元.
合作交流,探究新知
当y=194时,194=0.7x-16
解得 x=300
即6月份的用电量为300kW·h
在自变量的不同取值范围内,函数关系的表达式有不同的形式,这样的函数称为分段函数,分段函数在生活中也有很多应用.
分段函数
0.6x (0≤x≤160)
0.7x-16 (x>160)
y =
1.信禾公共汽车公司规定:旅客可免费携带一定重量的行李,如果超过规定的重量,则需要购买行李车票,行李费用y(元)与行李重量x(千克)的函数关系如图所示
6
10
80
30
x(千克)
60
y(元)
0
你能通过图象给出的信息知道旅客最多可免费携带多少千克的行李?
解决问题,应用新知
2.某市出租车计费方式如图所示.根据图象信息,下列说法错误的是( )
A. 出租车起步价是10元
B.在3千米内只收起步价
C.超过3千米的部分每千米收3元
D.超过3千米时所需费用y与x之间的函数表达式是y=2x+4
C
解决问题,应用新知
3.某复印店复印收费y(元)与复印面数(8开纸)x(面)的函数图象如图所示,那么从图象中可以看出,复印100面以内,每面收费 元,复印超过100面的部分,每面收费 元
0.4
0.5
解决问题,应用新知
“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,它像乌龟提出挑战。
请根据图像说一说《新龟兔赛跑》的故事。
《新龟兔赛跑》
深入探究,拓展新知
兔子
乌龟
x/ 分钟
y/米
O
起点
终点
50
《新龟兔赛跑》
这一次,兔子先让乌龟先跑若干分钟,然后再开始追赶,结果他们同时到达终点。
兔子
乌龟
起点
终点
x/ 分钟
y/米
O
你能画出函数图像吗?
深入探究,拓展新知
起跑时存在路程差
起跑时存在时间差
图1
图2
起点
终点
兔子
乌龟
x/ 分钟
y/米
O
兔子
乌龟
x/ 分钟
y/米
O
起点
终点
深入探究,拓展新知
【例1】
甲、乙两地相距40km,小明8:00骑自行车由甲地去乙地,平均车速为8km/h;
小红10:00坐公共汽车也由甲地去乙地,平均车速为40km/h.设小明所用的时间为x(h),小明与甲地的距离为y1(km),小红离甲地的距离为y2(km).
(1)分别写出y1,y2与x之间的函数表达式.
(2)在同一个直角坐标系中,画出这两个函数的图象,并指出谁先到达乙地.
深入探究,拓展新知
解(2)
甲、乙两地相距40km,小明8:00点骑自行车由甲地去乙地,平均车速为8km/h;小红10:00坐公共汽车也由甲地去乙地,平均车速为40km/h.设小明所用的时间为x(h),小明与甲地的距离为y1(km),小红离甲地的距离为y2(km).
(2)在同一个直角坐标系中,画出这两个函数的图象,并指出谁先到达乙地.
x/ h
y/km
1
2
3
8
32
40
16
24
4
5
0
小红y2=40(x-2)
(0≤ x ≤5)
(2≤ x ≤3)
小明y1= 8x
y1= 8x
y2=40(x-2)
两个一次函数图像的交点有什么样的实际意义?
深入探究,拓展新知
(2.5,20)
1.某音像店对外出租光盘的收费标准是:每张光盘在出租后头两天的租金为0.8元/天,以后每天收0.5元.求一张光盘在租出后第n天的租金y(元)与时间t(天)之间的函数表达式.
解决问题,应用新知
2.某移动公司对于移动话费推出两种收费方式:
A方案:每月收取基本月租费25元,另收通话费为0.36元/min;
B方案:零月租费,通话费为0.5元/min.
(1)试写出A,B两种方案所付话费y(元)与通话时间t(min)之间的函数表达式;
(2)分别画出这两个函数的图象;
(3)熊老师每月通话300min,我选择哪种付费方式比较合算?
解决问题,应用新知
解(1) A方案:
B方案:
(2)这两个函数的图象如下
●
y = 25+0.36t(t≥0)
●
y = 0.5t(t≥0)
y = 25+0.36t(t≥0)
y = 0.5t (t≥0)
O
5
15
10
5
10
y / 元
t / min
30
15
25
35
A方案
O
1
3
2
1
2
3
y / 元
t / min
B方案
●
3.甲、乙二人骑自行车同时从张庄出发,沿同一路线去李庄.甲行驶20分钟因事耽误一会儿,事后继续按原速行驶.如图表示甲、乙二人骑自行车行驶的路程y(千米)随时间x(分)变化的图象(全程),根据图象回答下列问题:
(1)乙比甲晚多长时间到达李庄?
(2)甲因事耽误了多长时间?
(3)x为何值时,乙行驶的路程比甲行驶
的路程多1千米?
解决问题,应用新知
解决问题,应用新知
解 (3)
当 x=36或48时,乙行驶的路程比甲行驶的路程多1千米
①
3.甲、乙二人骑自行车同时从张庄出发,沿同一路线去李庄.甲行驶20分钟因事耽误一会儿,事后继续按原速行驶.如图表示甲、乙二人骑自行车行驶的路程y(千米)随时间x(分)变化的图象(全程),根据图象回答下列问题:
(3)x为何值时,乙行驶的路程比甲行驶的路程多1千米?
x ? 5 = 1
1
6
②
x ? ( x ? 5)= 1
1
6
1
4
解得x= 36
解得x= 48
y= x - 5
1
4
y= x
1
6
y= 5
归纳总结,深化新知
本节课你有哪些收获?
布置作业,巩固新知
1.“清明节”期间,王老师一家自驾游去了离家170千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
(1)求他们出发半小时时,离家多少千米?
(2)求出AB段图象的函数表达式;
(3)他们出发2小时时,离目的地还有多少千米?
布置作业,巩固新知
2.为响应绿色出行号召,越来越多的市民选择租用共享单车出行.已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式,下图描述了两种方式需支付金额y(元)与骑行时间x(时)之间的函数关系,根据图象回答下列问题:
(1)求手机支付金额y(元)与骑行时间x(时)的函数表达式;
(2)李老师经常骑行共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算?
布置作业,巩固新知
(选做题)3.在“美丽广西,清洁乡村”活动中,李家村村委会提出两种购买垃圾桶的方案.
方案1:买分类垃圾桶,需要费用3000元,以后每月的垃圾处理费用为250元;
方案2:买不分类垃圾桶,需要费用1000元,以后每月的垃圾处理费用为500元.
设方案1的购买费和每月垃圾处理费共为y1元,方案2的购买费和每月垃圾处理费共为y2元,交费时间为x个月.
(1)直接写出y1,y2与x之间的函数表达式(不用写自变量的取值范围);
(2)在同一坐标系中画出函数y1,y2的图象;
(3)在垃圾桶使用寿命相同的情况下,哪种方案省钱?
布置作业,巩固新知
(选做题)4.如图1所示,在A、B两地间有汽车站C站,客车由A地驶向C站,货车由B地驶向A地,两车同时出发,匀速行驶,图2是客车、货车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数关系图象.
(1)填空:A、B两地相距__________千米;
(2)求两小时后,货车离站C的路程y2与行驶时间x之间的函数关系式.
(3)客、货两车何时相遇?
?
谢谢!
-3
O
3
9
6
-3
3
6
9
x
y
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
