18.2.1矩形-2020-2021学年人教版八年级数学下册培优训练(Word版 含答案)
文档属性
| 名称 | 18.2.1矩形-2020-2021学年人教版八年级数学下册培优训练(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 106.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-03 15:55:04 | ||
图片预览

文档简介
18.2.1矩形
[必备]☆知识点
一、矩形的性质与判定
1.定义:有一个角是直角的平行四边形叫做矩形,也称为长方形.
2.性质:
角:矩形的四个角都是直角
对角线:矩形的对角线相等
3.判定:①有一个角是直角的平行四边形是矩形
②有三个角是直角的四边形是矩形
③对角线相等的平行四边形是矩形
例1:如图,在矩形ABCD中,对角线AC,BD相交于点O,∠BOC=120°,AB=6.
求:(1)对角线的长;(2)BC的长;(3)矩形ABCD的面积.
341757010795
例2:如图,在矩形ABCD中,AE⊥BD,∠DAE:∠BAE=3:1,求∠BAE,∠EAO的度数.
373570514605
例3:如图,已知AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.求证:四边形BCED是矩形.
3639820128905
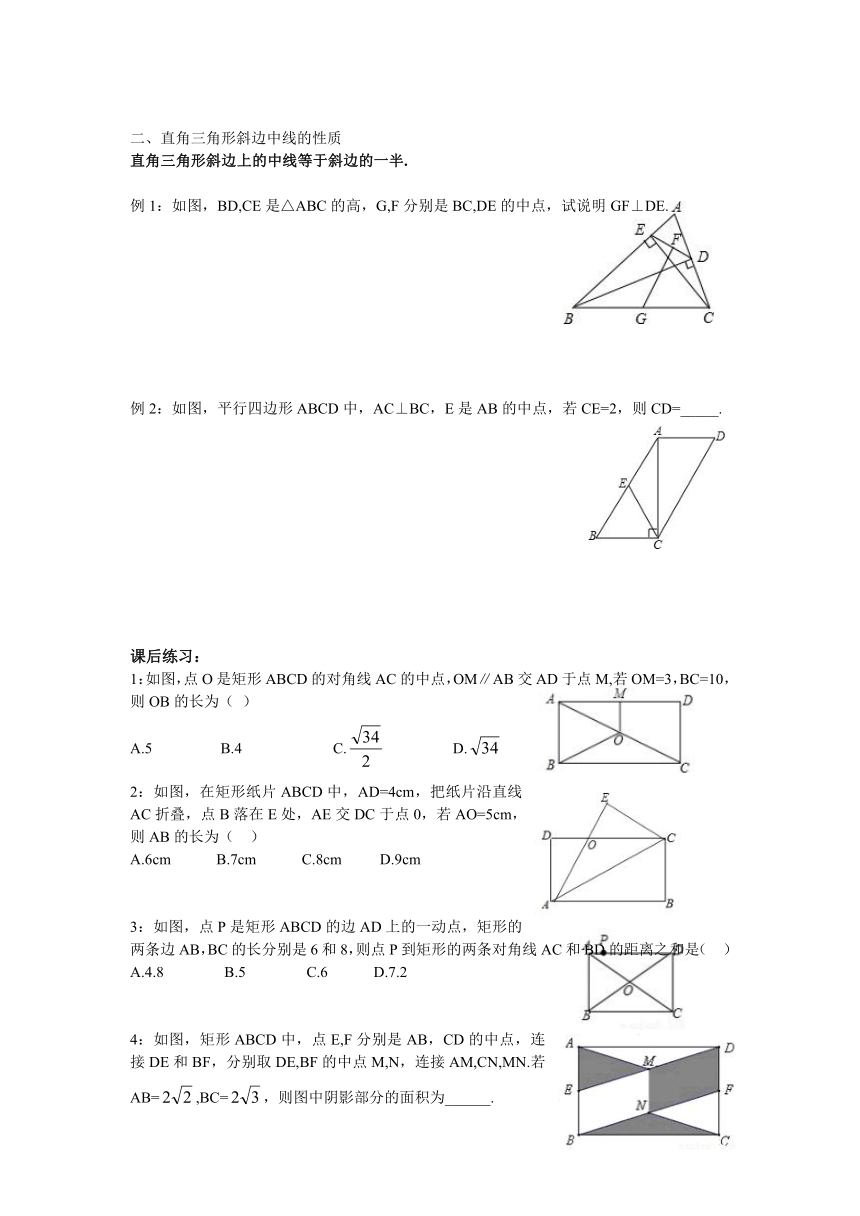
二、直角三角形斜边中线的性质
直角三角形斜边上的中线等于斜边的一半.
381000063500例1:如图,BD,CE是△ABC的高,G,F分别是BC,DE的中点,试说明GF⊥DE.
例2:如图,平行四边形ABCD中,AC⊥BC,E是AB的中点,若CE=2,则CD=_____.
403225059055
课后练习:
35883851612901:如图,点O是矩形ABCD的对角线AC的中点,OM∥AB交AD于点M,若OM=3,BC=10,则OB的长为( )
A.5 B.4 C.false D.false
35623501130302:如图,在矩形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点0,若AO=5cm,则AB的长为( )
A.6cm B.7cm C.8cm D.9cm
38715951047753:如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )
A.4.8 B.5 C.6 D.7.2
3763645596904:如图,矩形ABCD中,点E,F分别是AB,CD的中点,连接DE和BF,分别取DE,BF的中点M,N,连接AM,CN,MN.若AB=false,BC=false,则图中阴影部分的面积为______.
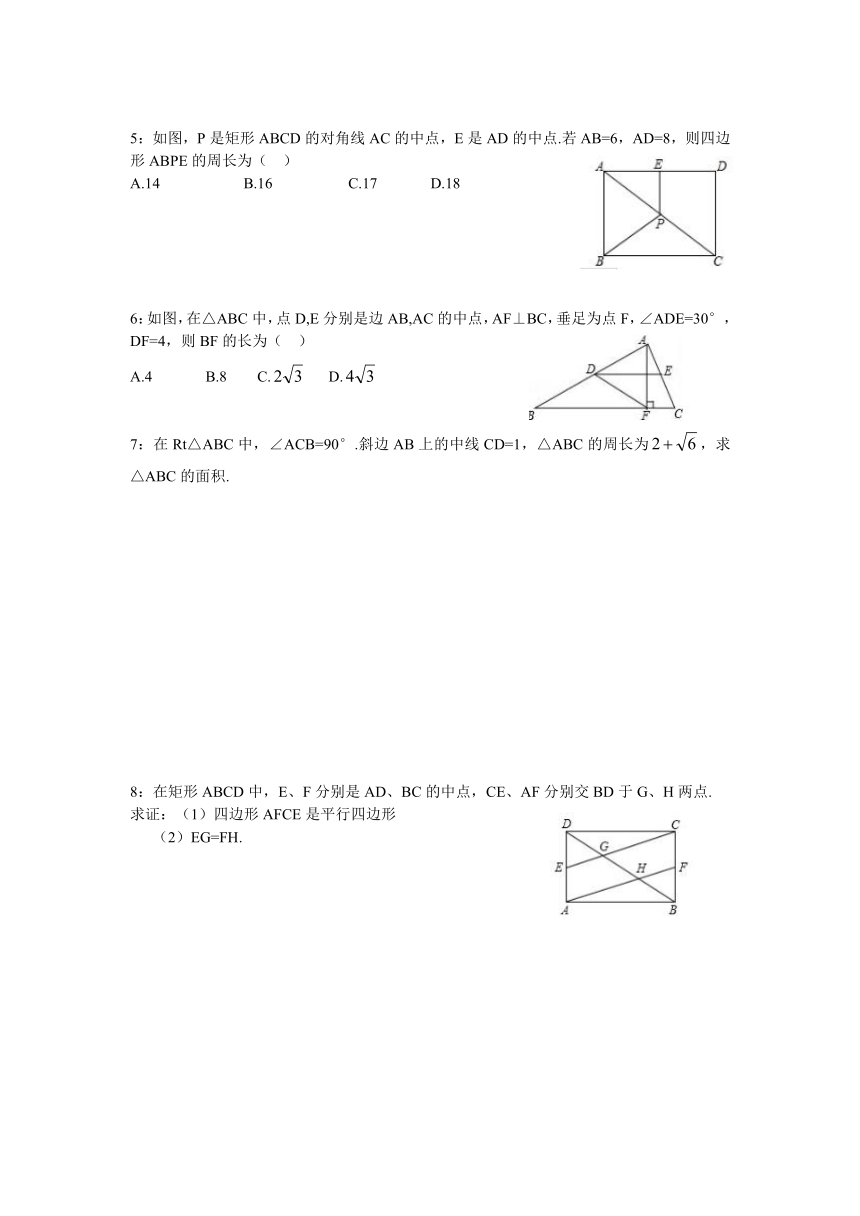
39573202635255:如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )
A.14 B.16 C.17 D.18
35134552273306:如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=4,则BF的长为( )
A.4 B.8 C.false D.false
7:在Rt△ABC中,∠ACB=90°.斜边AB上的中线CD=1,△ABC的周长为false,求△ABC的面积.
8:在矩形ABCD中,E、F分别是AD、BC的中点,CE、AF分别交BD于G、H两点.
369189083820求证:(1)四边形AFCE是平行四边形
EG=FH.
9:如图,在平行四边形ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
求证:四边形BECD是平行四边形
若∠A=50°,则当∠BOD=_____°时,四边形BECD是矩形.
3305810133985
10:如图,在矩形ABCD中,AB=24cm,BC=8cm,点P从A开始沿折线A→B→C→D以4cm/s的速度移动,点Q从C开始沿CD边以2cm/s的速度移动,如果点P,Q分别从A、C同时出发,当其中一点大大D时,另一点也随之停止运动,设运动时间为t s,当t为何值时,四边形QPBC为矩形?
31673801270
18.2.1矩形答案
一、矩形的性质与判定
例1:解:(1)∵四边形ABCD是矩形,
∴OA=OB= 12 BD.
又∵∠BOC=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴OB=AB=6,
∴对角线BD的长度是:BD=2OB=12;
(2)由(1)知,矩形ABCD的对角线长是12,则AC=12.
在直角△ABC中,AB=6,AC=12,则由勾股定理得到:BC=AC2+AB2=63;
(3)在矩形ABCD中,AB=6,BC=63,则该矩形的面积=AB?BC=6×63=363.
例2:证明:∵∠DAE:∠BAE=3:1
∠BAD=90°
∴∠BAE=22.5°
∠EAO=∠BAD-∠BAE=67.5°
∵AE⊥BD
即∠AED=90°
∴∠ADE=180-∠AED-∠EAO=22.5°
∵矩形的对角线互相平分
∴AO=DO
∴∠OAD=∠ODA=22.5°
∴∠EAO=∠BAD-∠BAE-∠OAD=45°
例3:证明:在△ABD和△ACE中,
∵AB=AC,AD=AE,∠BAD=∠CAE,
∴△ABD≌△ACE(SAS)
∴BD=CE又DE=BC.
∴四边形BCED为平行四边形.在△ACD和△ABE中,
∵AC=AB,AD=AE,∠CAD=∠CAB+∠BAD=∠CAB+∠CAE=∠BAE,
∴△ADC≌△AEB(SAS),∴CD=BE.
∴四边形BCED为矩形.(对角线相等的平行四边形是矩形)
二、直角三角形斜边中线的性质
例1:证明:如图,连接EG、DG,
∵BD、CE分别是△ABC的AC、AB边上的高,点G是BC的中点,
∴DG=EG=12BC,
∵点F是DE的中点,
∴GF⊥DE.
例2:答案:4
课后练习:
1.答案:D
2.答案:C
3.答案:A
4.答案:26
5.答案:D
6.答案:D
7.解:∵CD是直角三角形斜边上的高
∴2CD=AB=2
∵AC+BC=2+√6-2=√6
且AC?+BC?=AB?=4
(AC+BC)?-(AC?+BC?)=2AC×BC=2
∴AC×BC=1
S△=1/2AC×BC=1/2
8.证:
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∵E、F分别是AD、BC的中点,
∴AE=1212AD,CF=1212BC,
∴AE=CF,
∴四边形AFCE是平行四边形;
(2)∵四边形AFCE是平行四边形,
∴CE∥AF,
∴∠DGE=∠AHD=∠BHF,
∵AB∥CD,
∴∠EDG=∠FBH,
在△DEG和△BFH中,∠DGE=∠BHF,∠EDG=∠FBH,DE=BF,∴△DEG≌△BFH(AAS),
∴EG=FH.
9.解(1)证明:∵四边形ABCD为平行四边形,
∴AB∥DC,AB=CD,
∴∠OEB=∠ODC,
又∵O为BC的中点,
∴BO=CO,
在△BOE和△COD中,?????∠OEB=∠ODC∠BOE=∠CODBO=CO{∠OEB=∠ODC∠BOE=∠CODBO=CO,
∴△BOE≌△COD(AAS);
∴OE=OD,
∴四边形BECD是平行四边形;
(2)解:若∠A=50°,则当∠BOD=100°时,四边形BECD是矩形.理由如下:
∵四边形ABCD是平行四边形,
∴∠BCD=∠A=50°,
∵∠BOD=∠BCD+∠ODC,
∴∠ODC=100°-50°=50°=∠BCD,
∴OC=OD,
∵BO=CO,OD=OE,
∴DE=BC,
∵四边形BECD是平行四边形,
∴四边形BECD是矩形;
故答案为:100.
10.解:根据题意得:CQ=2t,AP=4t,
则BP=24-4t,
∵四边形ABCD是矩形,
∴∠B=∠C=90°,CD∥AB,
∴只有CQ=BP时,四边形QPBC是矩形,
即2t=24-4t,
解得:t=4,
答:当t=4s时,四边形QPBC是矩形.
[必备]☆知识点
一、矩形的性质与判定
1.定义:有一个角是直角的平行四边形叫做矩形,也称为长方形.
2.性质:
角:矩形的四个角都是直角
对角线:矩形的对角线相等
3.判定:①有一个角是直角的平行四边形是矩形
②有三个角是直角的四边形是矩形
③对角线相等的平行四边形是矩形
例1:如图,在矩形ABCD中,对角线AC,BD相交于点O,∠BOC=120°,AB=6.
求:(1)对角线的长;(2)BC的长;(3)矩形ABCD的面积.
341757010795
例2:如图,在矩形ABCD中,AE⊥BD,∠DAE:∠BAE=3:1,求∠BAE,∠EAO的度数.
373570514605
例3:如图,已知AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.求证:四边形BCED是矩形.
3639820128905
二、直角三角形斜边中线的性质
直角三角形斜边上的中线等于斜边的一半.
381000063500例1:如图,BD,CE是△ABC的高,G,F分别是BC,DE的中点,试说明GF⊥DE.
例2:如图,平行四边形ABCD中,AC⊥BC,E是AB的中点,若CE=2,则CD=_____.
403225059055
课后练习:
35883851612901:如图,点O是矩形ABCD的对角线AC的中点,OM∥AB交AD于点M,若OM=3,BC=10,则OB的长为( )
A.5 B.4 C.false D.false
35623501130302:如图,在矩形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点0,若AO=5cm,则AB的长为( )
A.6cm B.7cm C.8cm D.9cm
38715951047753:如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )
A.4.8 B.5 C.6 D.7.2
3763645596904:如图,矩形ABCD中,点E,F分别是AB,CD的中点,连接DE和BF,分别取DE,BF的中点M,N,连接AM,CN,MN.若AB=false,BC=false,则图中阴影部分的面积为______.
39573202635255:如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )
A.14 B.16 C.17 D.18
35134552273306:如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=4,则BF的长为( )
A.4 B.8 C.false D.false
7:在Rt△ABC中,∠ACB=90°.斜边AB上的中线CD=1,△ABC的周长为false,求△ABC的面积.
8:在矩形ABCD中,E、F分别是AD、BC的中点,CE、AF分别交BD于G、H两点.
369189083820求证:(1)四边形AFCE是平行四边形
EG=FH.
9:如图,在平行四边形ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
求证:四边形BECD是平行四边形
若∠A=50°,则当∠BOD=_____°时,四边形BECD是矩形.
3305810133985
10:如图,在矩形ABCD中,AB=24cm,BC=8cm,点P从A开始沿折线A→B→C→D以4cm/s的速度移动,点Q从C开始沿CD边以2cm/s的速度移动,如果点P,Q分别从A、C同时出发,当其中一点大大D时,另一点也随之停止运动,设运动时间为t s,当t为何值时,四边形QPBC为矩形?
31673801270
18.2.1矩形答案
一、矩形的性质与判定
例1:解:(1)∵四边形ABCD是矩形,
∴OA=OB= 12 BD.
又∵∠BOC=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴OB=AB=6,
∴对角线BD的长度是:BD=2OB=12;
(2)由(1)知,矩形ABCD的对角线长是12,则AC=12.
在直角△ABC中,AB=6,AC=12,则由勾股定理得到:BC=AC2+AB2=63;
(3)在矩形ABCD中,AB=6,BC=63,则该矩形的面积=AB?BC=6×63=363.
例2:证明:∵∠DAE:∠BAE=3:1
∠BAD=90°
∴∠BAE=22.5°
∠EAO=∠BAD-∠BAE=67.5°
∵AE⊥BD
即∠AED=90°
∴∠ADE=180-∠AED-∠EAO=22.5°
∵矩形的对角线互相平分
∴AO=DO
∴∠OAD=∠ODA=22.5°
∴∠EAO=∠BAD-∠BAE-∠OAD=45°
例3:证明:在△ABD和△ACE中,
∵AB=AC,AD=AE,∠BAD=∠CAE,
∴△ABD≌△ACE(SAS)
∴BD=CE又DE=BC.
∴四边形BCED为平行四边形.在△ACD和△ABE中,
∵AC=AB,AD=AE,∠CAD=∠CAB+∠BAD=∠CAB+∠CAE=∠BAE,
∴△ADC≌△AEB(SAS),∴CD=BE.
∴四边形BCED为矩形.(对角线相等的平行四边形是矩形)
二、直角三角形斜边中线的性质
例1:证明:如图,连接EG、DG,
∵BD、CE分别是△ABC的AC、AB边上的高,点G是BC的中点,
∴DG=EG=12BC,
∵点F是DE的中点,
∴GF⊥DE.
例2:答案:4
课后练习:
1.答案:D
2.答案:C
3.答案:A
4.答案:26
5.答案:D
6.答案:D
7.解:∵CD是直角三角形斜边上的高
∴2CD=AB=2
∵AC+BC=2+√6-2=√6
且AC?+BC?=AB?=4
(AC+BC)?-(AC?+BC?)=2AC×BC=2
∴AC×BC=1
S△=1/2AC×BC=1/2
8.证:
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∵E、F分别是AD、BC的中点,
∴AE=1212AD,CF=1212BC,
∴AE=CF,
∴四边形AFCE是平行四边形;
(2)∵四边形AFCE是平行四边形,
∴CE∥AF,
∴∠DGE=∠AHD=∠BHF,
∵AB∥CD,
∴∠EDG=∠FBH,
在△DEG和△BFH中,∠DGE=∠BHF,∠EDG=∠FBH,DE=BF,∴△DEG≌△BFH(AAS),
∴EG=FH.
9.解(1)证明:∵四边形ABCD为平行四边形,
∴AB∥DC,AB=CD,
∴∠OEB=∠ODC,
又∵O为BC的中点,
∴BO=CO,
在△BOE和△COD中,?????∠OEB=∠ODC∠BOE=∠CODBO=CO{∠OEB=∠ODC∠BOE=∠CODBO=CO,
∴△BOE≌△COD(AAS);
∴OE=OD,
∴四边形BECD是平行四边形;
(2)解:若∠A=50°,则当∠BOD=100°时,四边形BECD是矩形.理由如下:
∵四边形ABCD是平行四边形,
∴∠BCD=∠A=50°,
∵∠BOD=∠BCD+∠ODC,
∴∠ODC=100°-50°=50°=∠BCD,
∴OC=OD,
∵BO=CO,OD=OE,
∴DE=BC,
∵四边形BECD是平行四边形,
∴四边形BECD是矩形;
故答案为:100.
10.解:根据题意得:CQ=2t,AP=4t,
则BP=24-4t,
∵四边形ABCD是矩形,
∴∠B=∠C=90°,CD∥AB,
∴只有CQ=BP时,四边形QPBC是矩形,
即2t=24-4t,
解得:t=4,
答:当t=4s时,四边形QPBC是矩形.
