6.3三角形的中位线-2020-2021学年北师大版八年级数学下册课件(共18张PPT)
文档属性
| 名称 | 6.3三角形的中位线-2020-2021学年北师大版八年级数学下册课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 524.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-03 21:09:16 | ||
图片预览





文档简介
6.3 三角形的中位线
第六章 平行四边形
重点难点
3.利用三角形中位线定理解决问题.(难点)
1.理解并掌握三角形中位线的概念
2.理解并掌握三角形中位线的性质定理及其推导过程(重点)
平行四边形的性质与判定
性质
判定
边
角
对角线
推论
平行四边形的①两组对边分别平行②两组对边分别相等
平行四边形的①对角相等②邻角互补
平行四边形的对角线互相平分
夹在两条平行线间的平行线段相等
①两组对边分别平行的四边形
②两组对边分别相等的四边形
③一组对边平行且相等的四边形
两组对角分别相等的四边形
对角线互相平分四边形
复习导入
预习检测
连接三角形两边中点的线段叫做 .
三角形的中位线
三角形中位线定理:三角形的中位线 于第三边,且等于第三边的 .
一半
平行
你能将任意一个三角形分成四个全等的三角形吗?
连接每两边的中点,看看得到了什么样的图形?
四个全等的三角形.
你能设法验证上面的结论吗?
连接三角形两边中点的线段叫做三角形的中位线.
猜一猜,三角形中位线有什么性质?
B
C
A
D·
·E
·F
新课讲授
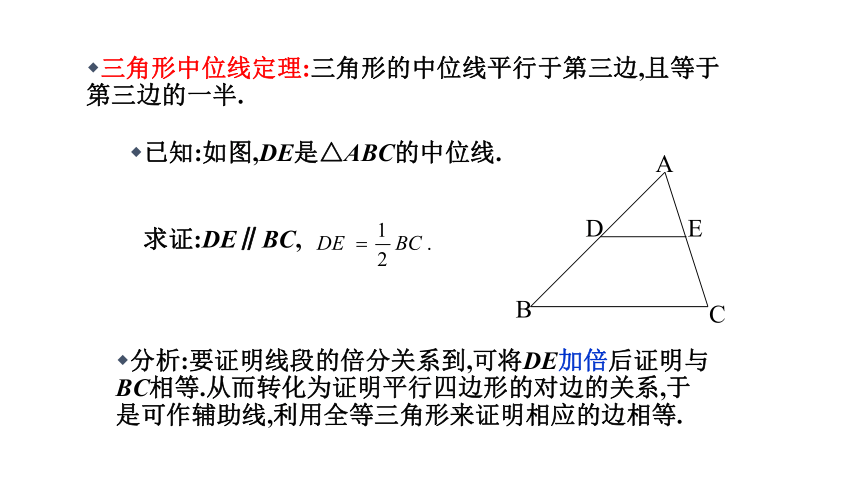
三角形中位线定理:三角形的中位线平行于第三边,且等于第三边的一半.
已知:如图,DE是△ABC的中位线.
分析:要证明线段的倍分关系到,可将DE加倍后证明与BC相等.从而转化为证明平行四边形的对边的关系,于是可作辅助线,利用全等三角形来证明相应的边相等.
D
E
B
C
A
求证:DE∥BC,
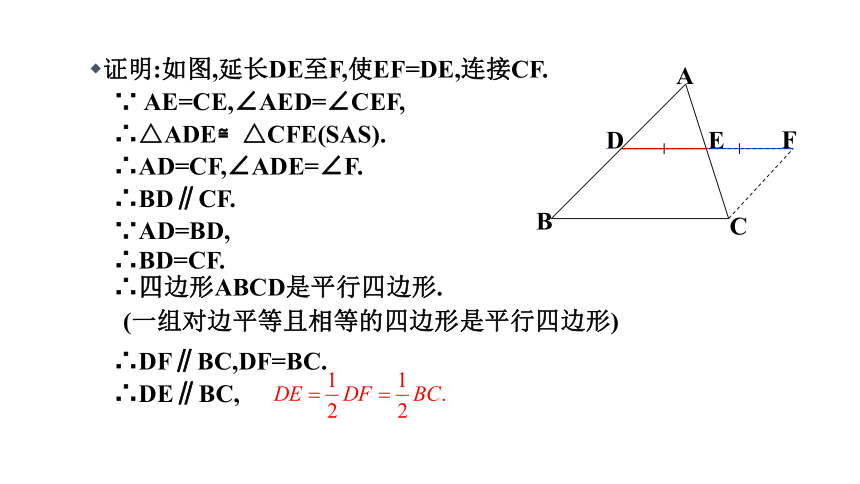
证明:如图,延长DE至F,使EF=DE,连接CF.
∵ AE=CE,∠AED=∠CEF,
∴△ADE≌△CFE(SAS).
∴AD=CF,∠ADE=∠F.
∴BD∥CF.
∵AD=BD,
∴BD=CF.
D
E
B
C
A
F
∴四边形ABCD是平行四边形.
∴DF∥BC,DF=BC.
∴DE∥BC,
(一组对边平等且相等的四边形是平行四边形)
三角形中位线性质的运用
利用定理“三角形的中位线平行于第三边,且等于第三边的一半”,请你证明下面分割出的四个小三角形全等.
已知:如图,D,E,F分别是△ABC各边的中点.
求证: △ADE≌△DBF≌△EFC≌△FED.
B
C
A
D
E
F
证明:
∵ D,E,F分别是△ABC各边的中点.
(三角形的中位线平行于第三边,且等于第三边的一半).
∴△ADE≌△DBF≌△EFC≌△FED(SSS).
分析:利用三角形中位线性质,可转化用(SSS)来证明三角形全等.
运用中位线的 “模型”
如图,四边形ABCD四边的中点分别为E,F,G,H,四边形EFGH是怎样四边形?你的结论对所有的四边形ABCD都成立吗?
猜想:四边形EFGH是平行四边形.这个结论对所有的四边形ABCD都成立.
求证:四边形EFGH是平行四边形.
A
B
C
H
D
E
F
G
已知:如图,在四边形ABCD中, E,F,G,H分别为各边的中点.
证明:连接AC.
∵E,F,G,H分别为各边的中点,
∴ EF∥HG, EF=HG.
∴EF∥AC,
HG∥AC,
∴四边形EFGH是平行四边形.
A
B
C
H
D
E
F
G
例.如图,在等边三角形 ABC 中,点 D,E 分别是边 BC,AC的中点,过点E作 EF⊥DE,交 BC 的延长线于点
F,求∠F的度数.
解:∵△ABC 是等边三角形,
∴∠B =60°.
∵点 D,E 分别是边BC,AC 的中点,
∴DE∥AB,
∴∠EDC= ∠B =60°
∵EF⊥DE,∴∠DEF =90°.
∴ ∠F =90°-∠EDC=30°
1.在△ABC 中,已知 D,E分别为边 AB,AC 的中点,连接 DE,若∠A=50° ,∠B=60°,则∠AED 等于( ).
A.70° B.67.5° C. 65° D.60°
2.如图,在?ABCD 中,AD =4,点 E,F 分别是 BD,CD的中点,则 EF 等于( )
A. 2 B.3 C.4 D.5
3.如图,?ABCD 的周长为 36,对角线 AC,BD 相交于
点O,点 E 是 CD 的中点,BD=12,则△DOE 的周长为( )
A.15 B.18 C.21 D.24D
A
A
A
随堂练习
已知:如图,△ABC点D是AB的中点,过D作DE∥BC交AC于E.
求证:DE是△ABC的中位线.
拓展提升
证明:过E作EF∥AB交BC于F,
F
∵DE∥BC,
∴四边形BFED是平行四边形.
∴∠ADE=∠B,
∴DB=EF.
∵点D是AB中点.∴AD=DB
∴AD=EF.
∴△ADE≌△EFC.
∴AE=EC.
∴点E是AC中点.
∴DE是△ABC的中位线.
∴∠A=∠CEF,∠B=∠EFC
∴∠ADE=∠EFC
三角形中位线的性质
定理:三角形的中位线平行于第三边,且等于第三边的一半.
这个定理提供了证明线段平行,和线段成倍分关系的根据.
∵DE是△ABC的中位,
D
E
B
C
A
∴DE∥BC,
课堂小结
应用模型:连接任意四边形各边中点所成的四边形是平行四边形.
要重视这个模型的证明过程反映出来的规律:对角线的关系是关键.改变四边形的形状后,对角线具有的关系(对角线相等,对角线垂直,对角线相等且垂直)决定了各中点所成四边形的形状.
A
B
C
H
D
E
F
G
第六章 平行四边形
重点难点
3.利用三角形中位线定理解决问题.(难点)
1.理解并掌握三角形中位线的概念
2.理解并掌握三角形中位线的性质定理及其推导过程(重点)
平行四边形的性质与判定
性质
判定
边
角
对角线
推论
平行四边形的①两组对边分别平行②两组对边分别相等
平行四边形的①对角相等②邻角互补
平行四边形的对角线互相平分
夹在两条平行线间的平行线段相等
①两组对边分别平行的四边形
②两组对边分别相等的四边形
③一组对边平行且相等的四边形
两组对角分别相等的四边形
对角线互相平分四边形
复习导入
预习检测
连接三角形两边中点的线段叫做 .
三角形的中位线
三角形中位线定理:三角形的中位线 于第三边,且等于第三边的 .
一半
平行
你能将任意一个三角形分成四个全等的三角形吗?
连接每两边的中点,看看得到了什么样的图形?
四个全等的三角形.
你能设法验证上面的结论吗?
连接三角形两边中点的线段叫做三角形的中位线.
猜一猜,三角形中位线有什么性质?
B
C
A
D·
·E
·F
新课讲授
三角形中位线定理:三角形的中位线平行于第三边,且等于第三边的一半.
已知:如图,DE是△ABC的中位线.
分析:要证明线段的倍分关系到,可将DE加倍后证明与BC相等.从而转化为证明平行四边形的对边的关系,于是可作辅助线,利用全等三角形来证明相应的边相等.
D
E
B
C
A
求证:DE∥BC,
证明:如图,延长DE至F,使EF=DE,连接CF.
∵ AE=CE,∠AED=∠CEF,
∴△ADE≌△CFE(SAS).
∴AD=CF,∠ADE=∠F.
∴BD∥CF.
∵AD=BD,
∴BD=CF.
D
E
B
C
A
F
∴四边形ABCD是平行四边形.
∴DF∥BC,DF=BC.
∴DE∥BC,
(一组对边平等且相等的四边形是平行四边形)
三角形中位线性质的运用
利用定理“三角形的中位线平行于第三边,且等于第三边的一半”,请你证明下面分割出的四个小三角形全等.
已知:如图,D,E,F分别是△ABC各边的中点.
求证: △ADE≌△DBF≌△EFC≌△FED.
B
C
A
D
E
F
证明:
∵ D,E,F分别是△ABC各边的中点.
(三角形的中位线平行于第三边,且等于第三边的一半).
∴△ADE≌△DBF≌△EFC≌△FED(SSS).
分析:利用三角形中位线性质,可转化用(SSS)来证明三角形全等.
运用中位线的 “模型”
如图,四边形ABCD四边的中点分别为E,F,G,H,四边形EFGH是怎样四边形?你的结论对所有的四边形ABCD都成立吗?
猜想:四边形EFGH是平行四边形.这个结论对所有的四边形ABCD都成立.
求证:四边形EFGH是平行四边形.
A
B
C
H
D
E
F
G
已知:如图,在四边形ABCD中, E,F,G,H分别为各边的中点.
证明:连接AC.
∵E,F,G,H分别为各边的中点,
∴ EF∥HG, EF=HG.
∴EF∥AC,
HG∥AC,
∴四边形EFGH是平行四边形.
A
B
C
H
D
E
F
G
例.如图,在等边三角形 ABC 中,点 D,E 分别是边 BC,AC的中点,过点E作 EF⊥DE,交 BC 的延长线于点
F,求∠F的度数.
解:∵△ABC 是等边三角形,
∴∠B =60°.
∵点 D,E 分别是边BC,AC 的中点,
∴DE∥AB,
∴∠EDC= ∠B =60°
∵EF⊥DE,∴∠DEF =90°.
∴ ∠F =90°-∠EDC=30°
1.在△ABC 中,已知 D,E分别为边 AB,AC 的中点,连接 DE,若∠A=50° ,∠B=60°,则∠AED 等于( ).
A.70° B.67.5° C. 65° D.60°
2.如图,在?ABCD 中,AD =4,点 E,F 分别是 BD,CD的中点,则 EF 等于( )
A. 2 B.3 C.4 D.5
3.如图,?ABCD 的周长为 36,对角线 AC,BD 相交于
点O,点 E 是 CD 的中点,BD=12,则△DOE 的周长为( )
A.15 B.18 C.21 D.24D
A
A
A
随堂练习
已知:如图,△ABC点D是AB的中点,过D作DE∥BC交AC于E.
求证:DE是△ABC的中位线.
拓展提升
证明:过E作EF∥AB交BC于F,
F
∵DE∥BC,
∴四边形BFED是平行四边形.
∴∠ADE=∠B,
∴DB=EF.
∵点D是AB中点.∴AD=DB
∴AD=EF.
∴△ADE≌△EFC.
∴AE=EC.
∴点E是AC中点.
∴DE是△ABC的中位线.
∴∠A=∠CEF,∠B=∠EFC
∴∠ADE=∠EFC
三角形中位线的性质
定理:三角形的中位线平行于第三边,且等于第三边的一半.
这个定理提供了证明线段平行,和线段成倍分关系的根据.
∵DE是△ABC的中位,
D
E
B
C
A
∴DE∥BC,
课堂小结
应用模型:连接任意四边形各边中点所成的四边形是平行四边形.
要重视这个模型的证明过程反映出来的规律:对角线的关系是关键.改变四边形的形状后,对角线具有的关系(对角线相等,对角线垂直,对角线相等且垂直)决定了各中点所成四边形的形状.
A
B
C
H
D
E
F
G
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
