2020-2021学年苏科版七年级数学下册培优训练9.4.2乘法公式:平方差公式(机构)(word版含解析)
文档属性
| 名称 | 2020-2021学年苏科版七年级数学下册培优训练9.4.2乘法公式:平方差公式(机构)(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 383.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-03 23:40:09 | ||
图片预览


文档简介
9.4.2乘法公式:平方差公式-苏科版七年级数学下册 培优训练
一、选择题
1、下列各式中,能用平方差公式计算的是( )
A. B. C. D.(-)()
2、计算的最佳方法是( )
A.运用多项式乘多项式法则 B.运用平方差公式
C.运用单项式乘多项式法则 D.运用完全平方公式
3、下列计算正确的是 ( )
A.(x+y)2=x2+y2 B.(x-y)2=x2-2xy-y2 C.(x+1)(x-1)=x2-1 D.(x-1)2=x2-1
4、若(2a+3b)( )=4a2-9b2,则括号内应填的代数式是( )
A.-2a-3b B.2a+3b C.2a-3b D.3b-2a
5、( )= 4a4-9b4,括号内应填( )
A.2a2+3b2 B.2a2-3b2 C.-2a2-3b2 D.-2a2+3b2
6、下列运用平方差公式计算错误的是( )
A.(a+b)(a-b)=a2-b2 B.(x+1)(x-1)=x2-1
C.(2x+1)(2x-1)=2x2-1 D.(-a+b)(-a-b)=a2-b2
7、对于任意的整数n,能整除(n+3)(n-3)-(n+2)(n-2)的整数是( )
A.4 B.3 C.-5 D.2
8、的计算结果的个位数字是( )
A.8 B.6 C.2 D.0
9、若a2-b2=,a+b=,则a-b的值为( )
A.- B. C.1 D.2
10、如图所示,在边长为a的正方形中剪去一个边长为b(b
二、填空题
11、化简(x-1)(x+1)的结果是________
12、计算:=________
13、化简的结果是__________.
14、若,,则______.
15、填空:(1)(-2x+y)(2x+y)=______________; (2)(3a-2b)(________+2b)=9a2-4b2;
(3)100×99=(______+______)×(______-______)=(______)2-=________
16、计算:40372﹣8072×2019=_____.
17、(x-y)2(x+y)2-(x2+y2)2=________.
18、如图,根据阴影面积的两种不同的计算方法,验证了初中数学的哪个公式.答:_____________.
19、下图是从一个正方形中剪下一个小正方形后,拼成一个矩形的过程.
根据下图,写出一个正确的等式:__________.
20、若(-2a+A)(5b+B)=4a2-25b2,则A=________,B=________.
三、解答题
21、计算:
(1)(2x-y)(2x+y) (2)(-4a-b)(-4a+b)
(3)202×198 (4)20192-2017×2021
(5) (6)(b-2)(b2+4)(b+2)
(7)(2x+y)(2x﹣y)+y(2x+y).
22、先化简再求值.
(1)(a-2b)(a+2b)-(a-2b)2+8b2,其中a=-2,b=.
(2)(a+b)(a-b)-(a-2b),其中a=2,b=-1.
(3)(2x-y)(2x+y)-(2y+x2)(2y-x2),其中x=-1,y=-2.
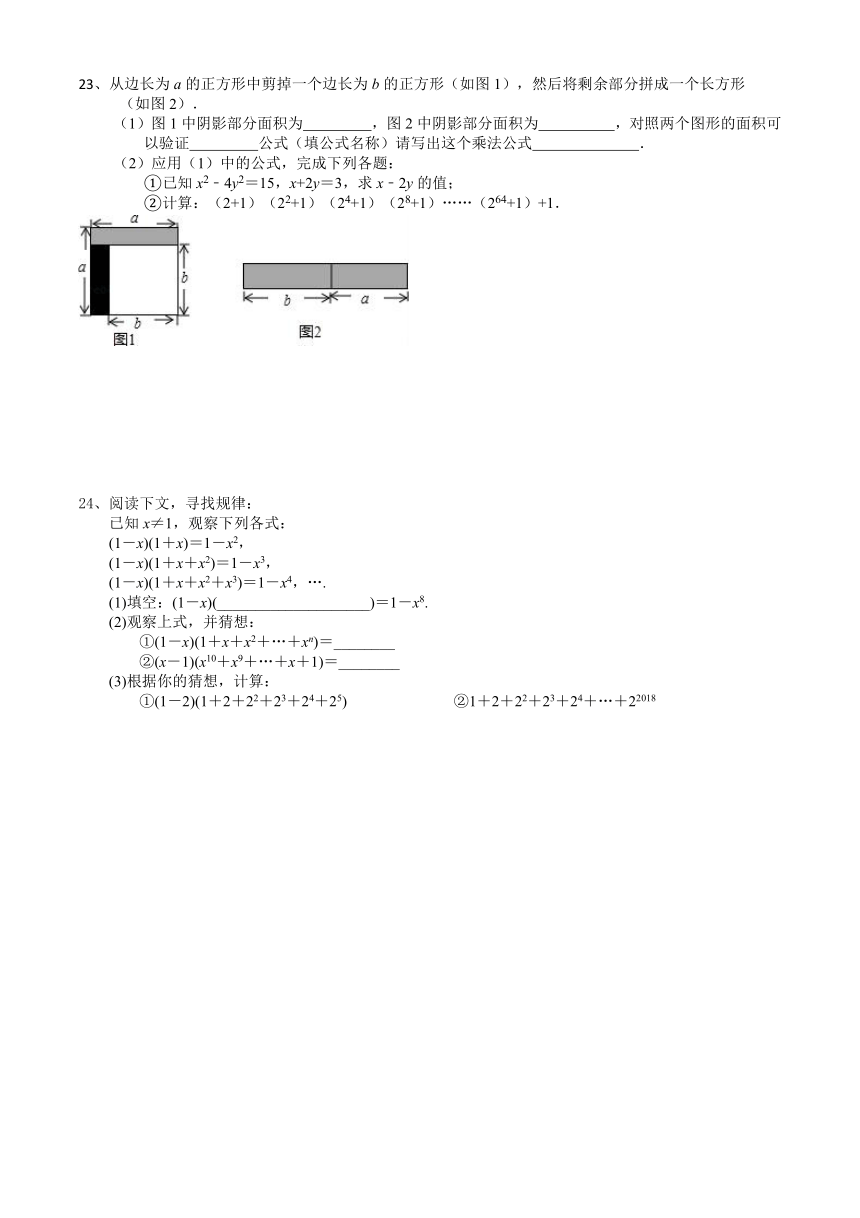
23、从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形
(如图2).
(1)图1中阴影部分面积为 ,图2中阴影部分面积为 ,对照两个图形的面积可以验证 公式(填公式名称)请写出这个乘法公式 .
(2)应用(1)中的公式,完成下列各题:
①已知x2﹣4y2=15,x+2y=3,求x﹣2y的值;
②计算:(2+1)(22+1)(24+1)(28+1)……(264+1)+1.
24、阅读下文,寻找规律:
已知x≠1,观察下列各式:
(1-x)(1+x)=1-x2,
(1-x)(1+x+x2)=1-x3,
(1-x)(1+x+x2+x3)=1-x4,….
(1)填空:(1-x)(____________________)=1-x8.
(2)观察上式,并猜想:
①(1-x)(1+x+x2+…+xn)=________
②(x-1)(x10+x9+…+x+1)=________
(3)根据你的猜想,计算:
①(1-2)(1+2+22+23+24+25) ②1+2+22+23+24+…+22018
9.4.2乘法公式:平方差公式-苏科版七年级数学下册 培优训练(答案)
一、选择题
1、下列各式中,能用平方差公式计算的是( B )
A. B. C. D.(-)()
2、计算的最佳方法是( B )
A.运用多项式乘多项式法则 B.运用平方差公式
C.运用单项式乘多项式法则 D.运用完全平方公式
3、下列计算正确的是 ( )
A.(x+y)2=x2+y2 B.(x-y)2=x2-2xy-y2 C.(x+1)(x-1)=x2-1 D.(x-1)2=x2-1
【解析】(x+y)2=x2+2xy+y2. (x-y)2=x2-2xy+y2.
(x+1)(x-1)=x2-1. (x-1)2=x2-2x+1. 故选C.
4、若(2a+3b)( )=4a2-9b2,则括号内应填的代数式是( )
A.-2a-3b B.2a+3b C.2a-3b D.3b-2a
[解析] 由(2a+3b)(2a-3b)=4a2-9b2,知括号内应填的代数式是2a-3b,故选C.
5、( )= 4a4-9b4,括号内应填( C )
A.2a2+3b2 B.2a2-3b2 C.-2a2-3b2 D.-2a2+3b2
6、下列运用平方差公式计算错误的是( )
A.(a+b)(a-b)=a2-b2 B.(x+1)(x-1)=x2-1
C.(2x+1)(2x-1)=2x2-1 D.(-a+b)(-a-b)=a2-b2
[解析] 运用平方差公式(a+b)(a-b)=a2-b2计算时,关键要找相同的项和互为相反数的项,其结果是相同项的平方减去互为相反数的项的平方.故选 C
7、对于任意的整数n,能整除(n+3)(n-3)-(n+2)(n-2)的整数是( C )
A.4 B.3 C.-5 D.2
【解析】 (n+3)(n-3)-(n+2)(n-2)=(n2-9)-(n2-4)=n2-9-n2+4=-5.故选C.
8、的计算结果的个位数字是( D)
A.8 B.6 C.2 D.0
9、若a2-b2=,a+b=,则a-b的值为( )
A.- B. C.1 D.2
[解析] 由(a+b)(a-b)= a2-b2知,(a-b)=,则a-b=.故选B
10、如图所示,在边长为a的正方形中剪去一个边长为b(b
[解析] 本题是一道数形结合创新题,通过图形的面积计算,验证乘法公式.
图①中的阴影部分面积是这两个正方形面积的差,即a2-b2,
又由于题图②的梯形的上底是2b,下底是2a,高为a-b,
所以梯形的面积为(2a+2b)(a-b)=(a+b)(a-b).
根据面积相等,得乘法公式:(a+b)(a-b)=a2-b2.
二、填空题
11、化简(x-1)(x+1)的结果是____x2-1____
12、计算:=________
[解析] =-n2=m2-n2.
13、化简的结果是__________.
解析:
14、若,,则__2019____.
15、填空:(1)(-2x+y)(2x+y)=______________; (2)(3a-2b)(________+2b)=9a2-4b2;
(3)100×99=(______+______)×(______-______)=(______)2-=________
答案:(1)y2-4x2 (2)3a (3)100 100 100 9999
16、计算:40372﹣8072×2019=___1__.
17、(x-y)2(x+y)2-(x2+y2)2=________.
【解析】(x-y)2(x+y)2-(x2+y2)2=[(x-y)(x+y)]2-(x2+y2)2=(x2-y2)2-(x2+y2)2
=[(x2-y2)+(x2+y2)][(x2-y2)-(x2+y2)]=-4x2y2.
答案:-4x2y2
18、如图,根据阴影面积的两种不同的计算方法,验证了初中数学的哪个公式.答:_____________.
答案:a2﹣b2=(a+b)(a﹣b)
19、下图是从一个正方形中剪下一个小正方形后,拼成一个矩形的过程.
根据下图,写出一个正确的等式:__________.
答案:
20、若(-2a+A)(5b+B)=4a2-25b2,则A=________,B=________.
[解析] 由等式右边可知B与-2a相同,A与5b互为相反数.[答案] -5b -2a
三、解答题
21、计算:
(1)(2x-y)(2x+y) (2)(-4a-b)(-4a+b)
(3)202×198 (4)20192-2017×2021
(5) (6)(b-2)(b2+4)(b+2)
(7)(2x+y)(2x﹣y)+y(2x+y).
解:(1)原式=(2x)2-(y)2=4x2-y2.
(2)原式=(-4a)2-b2=16a2-b2.
(3)202×198=(200+2)×(200-2)=2002-22=40000-4=39996.
(4)原式=20192-(2019-2)×(2019+2)
=20192-(20192-4)
=20192-20192+4
=4.
(5)原式=.
(6)(b-2)(b2+4)(b+2)=(b-2)(b+2)(b2+4)=(b2-4)(b2+4)=b4-16.
(7)(2x+y)(2x﹣y)+y(2x+y)=4x2﹣y2+2xy+y2=4x2+2xy.
22、先化简再求值.
(1)(a-2b)(a+2b)-(a-2b)2+8b2,其中a=-2,b=.
(2)(a+b)(a-b)-(a-2b)2,其中a=2,b=-1.
(3)(2x-y)(2x+y)-(2y+x2)(2y-x2),其中x=-1,y=-2.
【解析】(1)原式=a2-4b2-a2+4ab-4b2+8b2=4ab,
当a=-2,b=时,原式=-4.
(2)(a+b)(a-b)-(a-2b)2,其中a=2,b=-1.
(2)(a+b)(a-b)-(a-2b)2=a2-b2-a2+4ab-4b2=4ab-5b2,
当a=2,b=-1时,原式=4×2×(-1)-5×(-1)2=-13.
(3)原式=4x2-y2-(4y2-x4)=4x2-y2-4y2+x4=x4-5y2+4x2.
当x=-1,y=-2时,原式=(-1)4-5×(-2)2+4×(-1)2=-15.
23、从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形
(如图2).
(1)图1中阴影部分面积为 ,图2中阴影部分面积为 ,对照两个图形的面积可以验证 公式(填公式名称)请写出这个乘法公式 .
(2)应用(1)中的公式,完成下列各题:
①已知x2﹣4y2=15,x+2y=3,求x﹣2y的值;
②计算:(2+1)(22+1)(24+1)(28+1)……(264+1)+1.
解:(1)图1中阴影部分面积为a2﹣b2,图2中阴影部分面积为(a+b)(a﹣b),
对照两个图形的面积可以验证平方差公式:a2﹣b2=(a+b)(a﹣b).
故答案为:a2﹣b2,(a+b)(a﹣b),平方差,a2﹣b2=(a+b)(a﹣b).
(2)①∵x2﹣4y2=(x+2y)(x﹣2y),∴15=3(x﹣2y),∴x﹣2y=5;
②(2+1)(22+1)(24+1)(28+1)……(264+1)+1
=(2﹣1)(2+1)(22+1)(24+1)(28+1)……(264+1)+1
=(22﹣1)(22+1)(24+1)(28+1)……(264+1)+1
=(24﹣1)(24+1)(28+1)……(264+1)+1
=(28﹣1)(28+1)……(264+1)+1
=(264﹣1)(264+1)+1
=2128﹣1+1
=2128.
24、阅读下文,寻找规律:
已知x≠1,观察下列各式:
(1-x)(1+x)=1-x2,
(1-x)(1+x+x2)=1-x3,
(1-x)(1+x+x2+x3)=1-x4,….
(1)填空:(1-x)(____________________)=1-x8.
(2)观察上式,并猜想:
①(1-x)(1+x+x2+…+xn)=________
②(x-1)(x10+x9+…+x+1)=________
(3)根据你的猜想,计算:
①(1-2)(1+2+22+23+24+25) ②1+2+22+23+24+…+22018
解:(1)1+x+x2+x3+x4+x5+x6+x7
(2)①1-xn+1 ②x11-1
(3)①-63
②因为(1-2)(1+2+22+23+24+…+22018)=1-22019,
所以1+2+22+23+24+…+22018=-(1-22019)=22019-1.
一、选择题
1、下列各式中,能用平方差公式计算的是( )
A. B. C. D.(-)()
2、计算的最佳方法是( )
A.运用多项式乘多项式法则 B.运用平方差公式
C.运用单项式乘多项式法则 D.运用完全平方公式
3、下列计算正确的是 ( )
A.(x+y)2=x2+y2 B.(x-y)2=x2-2xy-y2 C.(x+1)(x-1)=x2-1 D.(x-1)2=x2-1
4、若(2a+3b)( )=4a2-9b2,则括号内应填的代数式是( )
A.-2a-3b B.2a+3b C.2a-3b D.3b-2a
5、( )= 4a4-9b4,括号内应填( )
A.2a2+3b2 B.2a2-3b2 C.-2a2-3b2 D.-2a2+3b2
6、下列运用平方差公式计算错误的是( )
A.(a+b)(a-b)=a2-b2 B.(x+1)(x-1)=x2-1
C.(2x+1)(2x-1)=2x2-1 D.(-a+b)(-a-b)=a2-b2
7、对于任意的整数n,能整除(n+3)(n-3)-(n+2)(n-2)的整数是( )
A.4 B.3 C.-5 D.2
8、的计算结果的个位数字是( )
A.8 B.6 C.2 D.0
9、若a2-b2=,a+b=,则a-b的值为( )
A.- B. C.1 D.2
10、如图所示,在边长为a的正方形中剪去一个边长为b(b
二、填空题
11、化简(x-1)(x+1)的结果是________
12、计算:=________
13、化简的结果是__________.
14、若,,则______.
15、填空:(1)(-2x+y)(2x+y)=______________; (2)(3a-2b)(________+2b)=9a2-4b2;
(3)100×99=(______+______)×(______-______)=(______)2-=________
16、计算:40372﹣8072×2019=_____.
17、(x-y)2(x+y)2-(x2+y2)2=________.
18、如图,根据阴影面积的两种不同的计算方法,验证了初中数学的哪个公式.答:_____________.
19、下图是从一个正方形中剪下一个小正方形后,拼成一个矩形的过程.
根据下图,写出一个正确的等式:__________.
20、若(-2a+A)(5b+B)=4a2-25b2,则A=________,B=________.
三、解答题
21、计算:
(1)(2x-y)(2x+y) (2)(-4a-b)(-4a+b)
(3)202×198 (4)20192-2017×2021
(5) (6)(b-2)(b2+4)(b+2)
(7)(2x+y)(2x﹣y)+y(2x+y).
22、先化简再求值.
(1)(a-2b)(a+2b)-(a-2b)2+8b2,其中a=-2,b=.
(2)(a+b)(a-b)-(a-2b),其中a=2,b=-1.
(3)(2x-y)(2x+y)-(2y+x2)(2y-x2),其中x=-1,y=-2.
23、从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形
(如图2).
(1)图1中阴影部分面积为 ,图2中阴影部分面积为 ,对照两个图形的面积可以验证 公式(填公式名称)请写出这个乘法公式 .
(2)应用(1)中的公式,完成下列各题:
①已知x2﹣4y2=15,x+2y=3,求x﹣2y的值;
②计算:(2+1)(22+1)(24+1)(28+1)……(264+1)+1.
24、阅读下文,寻找规律:
已知x≠1,观察下列各式:
(1-x)(1+x)=1-x2,
(1-x)(1+x+x2)=1-x3,
(1-x)(1+x+x2+x3)=1-x4,….
(1)填空:(1-x)(____________________)=1-x8.
(2)观察上式,并猜想:
①(1-x)(1+x+x2+…+xn)=________
②(x-1)(x10+x9+…+x+1)=________
(3)根据你的猜想,计算:
①(1-2)(1+2+22+23+24+25) ②1+2+22+23+24+…+22018
9.4.2乘法公式:平方差公式-苏科版七年级数学下册 培优训练(答案)
一、选择题
1、下列各式中,能用平方差公式计算的是( B )
A. B. C. D.(-)()
2、计算的最佳方法是( B )
A.运用多项式乘多项式法则 B.运用平方差公式
C.运用单项式乘多项式法则 D.运用完全平方公式
3、下列计算正确的是 ( )
A.(x+y)2=x2+y2 B.(x-y)2=x2-2xy-y2 C.(x+1)(x-1)=x2-1 D.(x-1)2=x2-1
【解析】(x+y)2=x2+2xy+y2. (x-y)2=x2-2xy+y2.
(x+1)(x-1)=x2-1. (x-1)2=x2-2x+1. 故选C.
4、若(2a+3b)( )=4a2-9b2,则括号内应填的代数式是( )
A.-2a-3b B.2a+3b C.2a-3b D.3b-2a
[解析] 由(2a+3b)(2a-3b)=4a2-9b2,知括号内应填的代数式是2a-3b,故选C.
5、( )= 4a4-9b4,括号内应填( C )
A.2a2+3b2 B.2a2-3b2 C.-2a2-3b2 D.-2a2+3b2
6、下列运用平方差公式计算错误的是( )
A.(a+b)(a-b)=a2-b2 B.(x+1)(x-1)=x2-1
C.(2x+1)(2x-1)=2x2-1 D.(-a+b)(-a-b)=a2-b2
[解析] 运用平方差公式(a+b)(a-b)=a2-b2计算时,关键要找相同的项和互为相反数的项,其结果是相同项的平方减去互为相反数的项的平方.故选 C
7、对于任意的整数n,能整除(n+3)(n-3)-(n+2)(n-2)的整数是( C )
A.4 B.3 C.-5 D.2
【解析】 (n+3)(n-3)-(n+2)(n-2)=(n2-9)-(n2-4)=n2-9-n2+4=-5.故选C.
8、的计算结果的个位数字是( D)
A.8 B.6 C.2 D.0
9、若a2-b2=,a+b=,则a-b的值为( )
A.- B. C.1 D.2
[解析] 由(a+b)(a-b)= a2-b2知,(a-b)=,则a-b=.故选B
10、如图所示,在边长为a的正方形中剪去一个边长为b(b
[解析] 本题是一道数形结合创新题,通过图形的面积计算,验证乘法公式.
图①中的阴影部分面积是这两个正方形面积的差,即a2-b2,
又由于题图②的梯形的上底是2b,下底是2a,高为a-b,
所以梯形的面积为(2a+2b)(a-b)=(a+b)(a-b).
根据面积相等,得乘法公式:(a+b)(a-b)=a2-b2.
二、填空题
11、化简(x-1)(x+1)的结果是____x2-1____
12、计算:=________
[解析] =-n2=m2-n2.
13、化简的结果是__________.
解析:
14、若,,则__2019____.
15、填空:(1)(-2x+y)(2x+y)=______________; (2)(3a-2b)(________+2b)=9a2-4b2;
(3)100×99=(______+______)×(______-______)=(______)2-=________
答案:(1)y2-4x2 (2)3a (3)100 100 100 9999
16、计算:40372﹣8072×2019=___1__.
17、(x-y)2(x+y)2-(x2+y2)2=________.
【解析】(x-y)2(x+y)2-(x2+y2)2=[(x-y)(x+y)]2-(x2+y2)2=(x2-y2)2-(x2+y2)2
=[(x2-y2)+(x2+y2)][(x2-y2)-(x2+y2)]=-4x2y2.
答案:-4x2y2
18、如图,根据阴影面积的两种不同的计算方法,验证了初中数学的哪个公式.答:_____________.
答案:a2﹣b2=(a+b)(a﹣b)
19、下图是从一个正方形中剪下一个小正方形后,拼成一个矩形的过程.
根据下图,写出一个正确的等式:__________.
答案:
20、若(-2a+A)(5b+B)=4a2-25b2,则A=________,B=________.
[解析] 由等式右边可知B与-2a相同,A与5b互为相反数.[答案] -5b -2a
三、解答题
21、计算:
(1)(2x-y)(2x+y) (2)(-4a-b)(-4a+b)
(3)202×198 (4)20192-2017×2021
(5) (6)(b-2)(b2+4)(b+2)
(7)(2x+y)(2x﹣y)+y(2x+y).
解:(1)原式=(2x)2-(y)2=4x2-y2.
(2)原式=(-4a)2-b2=16a2-b2.
(3)202×198=(200+2)×(200-2)=2002-22=40000-4=39996.
(4)原式=20192-(2019-2)×(2019+2)
=20192-(20192-4)
=20192-20192+4
=4.
(5)原式=.
(6)(b-2)(b2+4)(b+2)=(b-2)(b+2)(b2+4)=(b2-4)(b2+4)=b4-16.
(7)(2x+y)(2x﹣y)+y(2x+y)=4x2﹣y2+2xy+y2=4x2+2xy.
22、先化简再求值.
(1)(a-2b)(a+2b)-(a-2b)2+8b2,其中a=-2,b=.
(2)(a+b)(a-b)-(a-2b)2,其中a=2,b=-1.
(3)(2x-y)(2x+y)-(2y+x2)(2y-x2),其中x=-1,y=-2.
【解析】(1)原式=a2-4b2-a2+4ab-4b2+8b2=4ab,
当a=-2,b=时,原式=-4.
(2)(a+b)(a-b)-(a-2b)2,其中a=2,b=-1.
(2)(a+b)(a-b)-(a-2b)2=a2-b2-a2+4ab-4b2=4ab-5b2,
当a=2,b=-1时,原式=4×2×(-1)-5×(-1)2=-13.
(3)原式=4x2-y2-(4y2-x4)=4x2-y2-4y2+x4=x4-5y2+4x2.
当x=-1,y=-2时,原式=(-1)4-5×(-2)2+4×(-1)2=-15.
23、从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形
(如图2).
(1)图1中阴影部分面积为 ,图2中阴影部分面积为 ,对照两个图形的面积可以验证 公式(填公式名称)请写出这个乘法公式 .
(2)应用(1)中的公式,完成下列各题:
①已知x2﹣4y2=15,x+2y=3,求x﹣2y的值;
②计算:(2+1)(22+1)(24+1)(28+1)……(264+1)+1.
解:(1)图1中阴影部分面积为a2﹣b2,图2中阴影部分面积为(a+b)(a﹣b),
对照两个图形的面积可以验证平方差公式:a2﹣b2=(a+b)(a﹣b).
故答案为:a2﹣b2,(a+b)(a﹣b),平方差,a2﹣b2=(a+b)(a﹣b).
(2)①∵x2﹣4y2=(x+2y)(x﹣2y),∴15=3(x﹣2y),∴x﹣2y=5;
②(2+1)(22+1)(24+1)(28+1)……(264+1)+1
=(2﹣1)(2+1)(22+1)(24+1)(28+1)……(264+1)+1
=(22﹣1)(22+1)(24+1)(28+1)……(264+1)+1
=(24﹣1)(24+1)(28+1)……(264+1)+1
=(28﹣1)(28+1)……(264+1)+1
=(264﹣1)(264+1)+1
=2128﹣1+1
=2128.
24、阅读下文,寻找规律:
已知x≠1,观察下列各式:
(1-x)(1+x)=1-x2,
(1-x)(1+x+x2)=1-x3,
(1-x)(1+x+x2+x3)=1-x4,….
(1)填空:(1-x)(____________________)=1-x8.
(2)观察上式,并猜想:
①(1-x)(1+x+x2+…+xn)=________
②(x-1)(x10+x9+…+x+1)=________
(3)根据你的猜想,计算:
①(1-2)(1+2+22+23+24+25) ②1+2+22+23+24+…+22018
解:(1)1+x+x2+x3+x4+x5+x6+x7
(2)①1-xn+1 ②x11-1
(3)①-63
②因为(1-2)(1+2+22+23+24+…+22018)=1-22019,
所以1+2+22+23+24+…+22018=-(1-22019)=22019-1.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
