第20章数据的分析 单元综合提升-2020-2021学年人教版八年级数学下册(Word版 含解析)
文档属性
| 名称 | 第20章数据的分析 单元综合提升-2020-2021学年人教版八年级数学下册(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 177.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-04 00:00:00 | ||
图片预览




文档简介
2021年人教版八年级数学下册《第20章数据的分析》单元综合同步提升训练(附答案)
1.已知一组数据1,0,3,﹣1,x,2,3的平均数是1,则这组数据的中位数是( )
A.﹣1 B.1 C.3 D.﹣1或者3
2.小林准备选择一个品牌开运动鞋网店.为此他到多个运动场地随机收集了500个人所穿运动鞋的品牌,对于这组数据他最想知道的是( )
A.众数 B.平均数 C.中位数 D.方差
3.有15名学生参加学校举办的“最强大脑”智力竞赛,比赛结束后根据每个学生的成绩计算平均数、中位数、众数、方差,若去掉一个最高分,一个最低分,则一定不会发生变化的是( )
A.平均数 B.中位数 C.众数 D.方差
4.参加第六届京津冀羽毛球冠军挑战赛的一个代表队的年龄分别是49,20,20,25,31,40,46,20,44,25,这组数据的平均数,众数,中位数分别是( )
A.33,21,27 B.32,20,28 C.33,49,27 D.32,21,22
5.数据201,202,198,199,200的方差与极差分别是( )
A.1,4 B.2,2 C.2,4 D.4,2
6.若x1,x2,x3,x4的平均数为4,x5,x6,x7,…,x10的平均数为6,则x1,x2,…,x10的平均数为( )
A.5 B.4.8 C.5.2 D.8
7.某校为了解学生的课外阅读情况,随机抽取了一个班级的学生,对他们一周的读书时间进行了统计,统计数据如表所示:
读书时间(小时) 7 8 9 10 11
学生人数 6 10 9 8 7
关于该班学生一周读书时间的数据有下列说法:
①一周读书时间数据的中位数是9小时;
②一周读书时间数据的众数是8小时;
③一周读书时间数据的平均数是9小时;
④一周读书时间不少于9小时的人数占抽查学生的50%.
其中说法正确的序号是( )
A.①②③ B.①②④ C.②③④ D.①③④
8.已知一组数据a1,a2,a3,a4,a5的方差是S1,另一组数据a1﹣6,a2﹣6,a3﹣6,a4﹣6,a5﹣6的方差是S2,则S1与S2的大小关系是S1 S2(填写“>”“<”或“=”).
9.甲、乙、丙、丁四人进行射击测试,每人测试10次,平均成绩均为9.2环,方差如表所示:则在这四个选手中,成绩最稳定的是 .
选手 甲 乙 丙 丁
方差 0.56 0.60 0.50 0.45
10.下表是某一时段15名乘客过地铁安检口测体温的数据:
体温(℃) 36.4 36.5 36.6 36.7 36.8 36.9 37.0
人数(人) 1 1 3 2 3 4 1
这组数据的中位数是 .
11.如果一组数据1,2,5,a,9的方差是3,则2,4,10,2a,18的方差是 .
12.小明用s2=[(x1﹣6)2+(x2﹣6)2+…+(x10﹣6)2]计算一组数据的方差,那么x1+x2+x3+…+x10= .
13.数学期末总评成绩是将平时、期中和期末的成绩按3:3:4计算,若小红平时、期中和期末的成绩分别是90分、80分、100分,则小红一学期的数学期末总评成绩是 分.
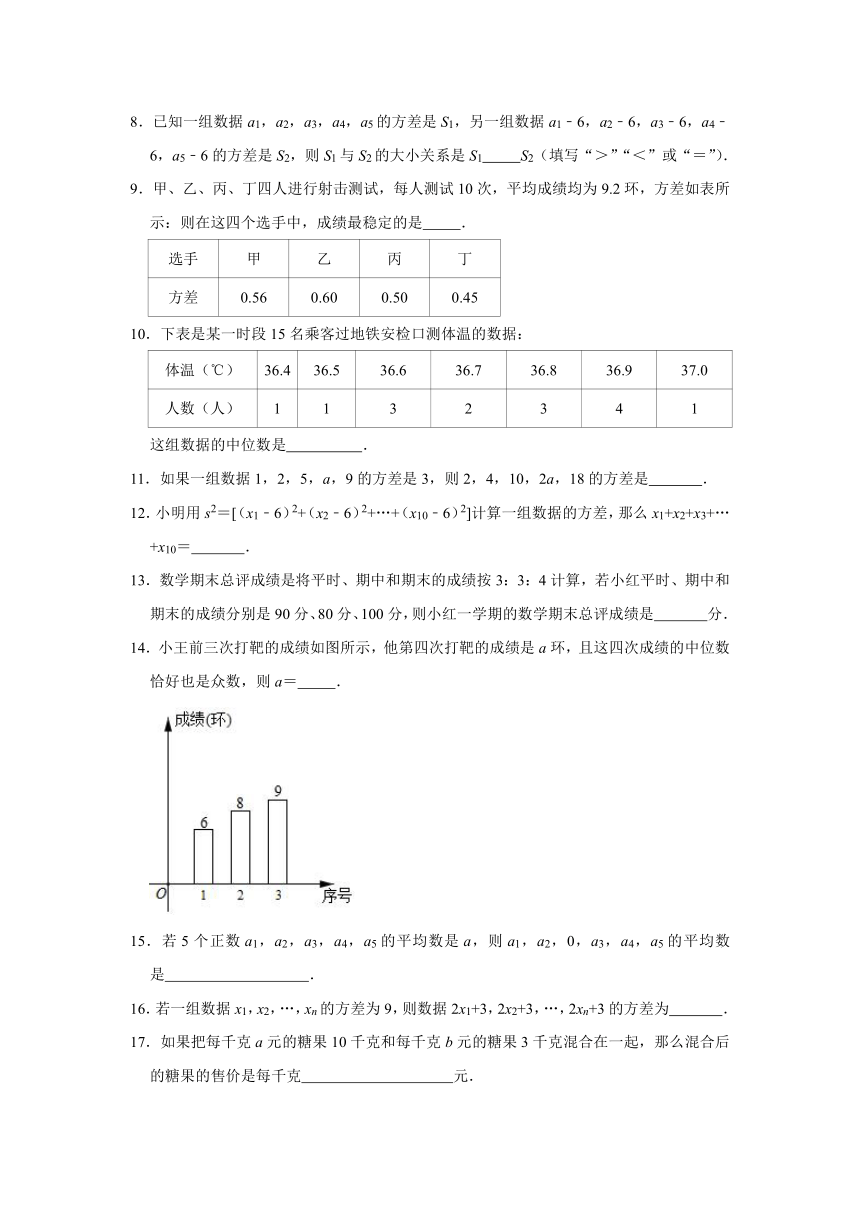
14.小王前三次打靶的成绩如图所示,他第四次打靶的成绩是a环,且这四次成绩的中位数恰好也是众数,则a= .
15.若5个正数a1,a2,a3,a4,a5的平均数是a,则a1,a2,0,a3,a4,a5的平均数是 .
16.若一组数据x1,x2,…,xn的方差为9,则数据2x1+3,2x2+3,…,2xn+3的方差为 .
17.如果把每千克a元的糖果10千克和每千克b元的糖果3千克混合在一起,那么混合后的糖果的售价是每千克 元.
18.已知2,3,5,m,n五个数据的方差是2,那么4,5,7,m+2,n+2五个数据的方差是 .
19.若一组数据3,4,5,x的极差是5,则x= .
20.一组数据2,3,4,x,6的平均数是4,则这组数据的方差是 .
21.下表是随机抽取的某公司部分员工的月收入资料:
月收入/元 20000 18000 8000 5000 4500 3400 3000 2000
人数 1 1 1 2 4 1 8 2
(1)请计算以上样本的平均数和中位数;
(2)甲乙两人分别用样本平均数和中位数来估计推断公司全体员工月收入水平,请你写出甲乙两人的推断结论;
(3)指出谁的推断比较科学合理,能真实地反映公司全体员工月收入水平,并说出另一个人的推断依据不能真实反映公司全体员工月收入水平的原因.
22.杭州市建兰中学开展防疫知识线上竞赛活动,九年级(1)、(2)班各选出5名选手参加竞赛,两个班选出的5名选手的竞赛成绩(满分为100分)如图所示.
(1)求九(1)班的众数和九(2)班的中位数;
(2)计算两个班竞赛成绩的方差,并说明哪个班的成绩较为整齐.
23.某集团旗下有两家酒店A,B,2020年下半年的月营业额统计如下:
[信息一]A,B两家酒店2020年下半年月营业额(单位:百万元)统计图如下
[信息二]A,B两家酒店2020年下半年月营业额的相关数据统计如下:
酒店 平均数 中位数 众数 方差
A 2.5 2.2 2.2 0.73
B 2.3 1.9 △ 0.59
(1)已知A酒店2020年11月份月营业额为3百万元,求A酒店2020年下半年的营业总额;
(2)求B酒店2020年8月份的月营业额,并补全[信息二]中缺失数据;
(3)结合数据分析,2020年下半年A,B两家酒店哪家经营状况较好,请说明理由.
24.小明本学期的数学成绩如表所示:
测验类别 平时成绩1 平时成绩2 平时成绩3 平时成绩4 平时平均数 期中考试 期末考试
成绩 108 103 101 108 a 110 114
(1)六次测试成绩的中位数和众数分别是什么?
(2)请计算出小明该学期的平时成绩平均分a的值;
(3)如果学期的数学总评成绩是根据一定的权重计算所得,其中平时成绩a所占权重为20%,已知小明该学期的总评成绩为111分,请计算出期中考试和期末考试各自所占权重.
25.某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,甲、乙两人射箭成绩统计表如下.
第1次 第2次 第3次 第4次 第5次
甲成绩 9 4 7 4 6
乙成绩 7 5 7 a 7
(1)求a的值和甲、乙的方差;
(2)请你从平均数和方差的角度分析,谁将被选中.
26.甲、乙两位同学5次数学选拔赛的成绩统计如表,他们5次考试的总成绩相同,请同学们完成下列问题:
第1次 第2次 第3次 第4次 第5次
甲成绩 80 40 70 50 60
乙成绩 70 50 70 a 70
(1)统计表中,a= ,甲同学成绩的极差为 ;
(2)小颖计算了甲同学的成绩平均数为60,方差是S甲2=[(80﹣60)2+(40﹣60)2+(70﹣60)2+(50﹣60)2+(60﹣60)2]=200.请你求出乙同学成绩的平均数和方差;
(3)从平均数和方差的角度分析,甲、乙两位同学谁的成绩更稳定.
27.为选派一名学生参加全市实践活动技能竞赛,A,B两位同学在学校实习基地单位时间内现场进行加工直径为20mm的零件的测试,他俩各加工的10个零件的相关数据依次如图表所示(单位mm):
平均数 方差 完全符合要求个数
A 20 0.026 2
B 20 SB2
根据测试得到的有关数据,试解答下列问题:
(1)考虑平均数与完全符合要求的个数,你认为哪个同学的成绩好些?
(2)计算出SB2的大小,考虑平均数与方差,说明谁的成绩好些?
(3)考虑图中折线走势,你认为派谁去参赛较合适?说明你的理由.
参考答案
1.解:∵一组数据1,0,3,﹣1,x,2,3的平均数是1,
∴[1+0+3+(﹣1)+x+2+3]÷7=1,
解得x=﹣1,
∴这组数据按照从小到大排列是:﹣1,﹣1,0,1,2,3,3,
∴这组数据的中位数是1,
故选:B.
2.解:这组数据他最想知道的是众数.
故选:A.
3.解:去掉一个最高分和一个最低分对中位数没有影响.
故选:B.
4.解:这组数据的平均数是:(49+20+20+25+31+40+46+20+44+25)÷10=32(岁),
这组数据出现最多的数是20,所以这组数据的众数是20岁;
把这些数按从小到大的顺序排列为:20,20,20,25,25,31,40,44,46,49,
则这组数据的中位数是:(25+31)÷2=28(岁).
故选:B.
5.解:极差为202﹣198=4,
∵平均数为=200,
∴方差为×[(201﹣200)2+(202﹣200)2+(198﹣200)2+(199﹣200)2+(200﹣200)2]=2,
故选:C.
6.解:由题意可得,
x1,x2,…,x10的平均数为:===5.2,
故选:C.
7.解:这个班级的学生总数是:6+10+9+8+7=40(人),
则该班学生一周读书时间数据的中位数是:(9+9)÷2=9(小时),说法①正确;
众数是:8小时,说法②正确;
平均数是:(7×6+8×10+9×9+10×8+11×7)=9(小时),说法③正确;
一周读书时间不少于9小时的人数占抽查学生的百分比为:×100%=60%,说法④错误.
故选:A.
8.解:根据题意知,数据a1﹣6,a2﹣6,a3﹣6,a4﹣6,a5﹣6是将数据a1,a2,a3,a4,a5分别减去6所得,
所以两组数据的波动幅度相同,
∴S1=S2,
故答案为:=.
9.解:∵0.60>0.56>0.50>0.45,
∴丁的方差最小,
∴成绩最稳定的是丁,
故答案为:丁.
10.解:将这组数据从小到大的顺序排列后,处于中间位置的那个数是36.8℃,那么由中位数的定义可知,这组数据的中位数是36.8℃.
故答案为:36.8℃.
11.解:∵数据1,2,5,a,9的方差是3,
∴2,4,10,2a,18的方差是22×3=12.
故答案为:12.
12.解:由s2=[(x1﹣6)2+(x2﹣6)2+…+(x10﹣6)2]知这10个数据的平均数为6,
所以x1+x2+x3+…+x10=6×10=60,
故答案为:60.
13.解:根据题意得:小红一学期的数学期末总评成绩是=91(分),
故答案为:91.
14.解:由统计图可知,前三次的中位数是8,
∵第四次打靶的成绩是a环,这四次成绩的中位数恰好也是众数,
∴a=8,
故答案为:8.
15.解:∵正数a1,a2,a3,a4,a5的平均数是a,
∴a1+a2+a3+a4+a5=5a,
∴(a1+a2+0+a3+a4+a5)=a;
故答案为:a.
16.解:设一组数据x1,x2…xn的方差S2=9,
则另一组数据2x1+3,2x2+3…2xn+3的S′2=22S2=36,
故答案为:36.
17.解:由题意可得,
混合后的糖果的售价是每千克(元),
故答案为:.
18.解:由题意知,原数据的平均数为,新数据的每一个数都加了2,则平均数变为+2,
则原来的方差S12=[(x1﹣)2+(x2﹣)2+…+(x5﹣)2]=2,
现在的方差S22=[(x1+2﹣﹣2)2+(x2+2﹣﹣2)2+…+(x5+2﹣﹣2)2]
=[(x1﹣)2+(x2﹣)2+…+(x5﹣)2]=2,
所以方差不变.
故答案为2.
19.解:①x是最小的数时,5﹣x=5,
解得x=0,
②x是最大的数时,x﹣3=5,
解得x=8,
所以,x的值为0或8.
故答案为:0或8.
20.解:∵数据2,3,4,x,6的平均数是4,
∴(2+3+4+x+6)÷5=4,
解得:x=5,
∴这组数据的方差是[(2﹣4)2+(3﹣4)2+(4﹣4)2+(5﹣4)2+(6﹣4)2]=2;
故答案为:2.
解:(1)样本平均数为
=5270(元),
将这20名员工的工资从小到大排列,处在中间位置的两个数的平均数为(3400+3000)÷2=3200(元),因此中位数是3200元,
答:平均数为5270元,中位数是3200元;
(2)甲:由样本平均数为5270元,估计全体员工月平均收入大约为5270元,
乙:由样本中位数为3200元,估计全体员工大约有一半的员工月收入超过3200元,有一半的员工月收入不足3200元;
(3)乙的推断比较科学合理.由题意知样本中的20名员工,只有3名员工的月收入在5270元以上,原因是该样本数据极差较大,所以平均数不能真实反映实际情况.
22.解:(1)由图知,九(1)班成绩为80、80、80、90、100,
九(2)班成绩为70、80、85、95、100,
所以九(1)班成绩的众数为80分,九(2)班成绩的中位数为85分;
(2)九(1)班成绩的平均数为=86(分),九(2)班成绩的平均数为=86(分),
∴九(1)班成绩的方差为×[3×(80﹣86)2+(90﹣86)2+(100﹣86)2]=64,
九(2)班成绩的方差为×[(70﹣86)2+(80﹣86)2+(85﹣86)2+(95﹣86)2+(100﹣86)2]=114,
∴九(1)班成绩较为整齐.
23.解:(1)2.5×6=15(百万元),
答:A酒店2020年下半年的营业总额为15百万元;
(2)B酒店下半年的总营业额为2.3×6=13.8(百万元),
因此B酒店8月份的营业额为13.8﹣1.5﹣1.7﹣2.3﹣1.7﹣3.6=3(百万元),
补全条形统计图如图所示:
(3)A酒店的经营状况较好,理由:A酒店经营营业额的平均数、中位数、众数均比B酒店的高.
24.解:(1)六次数据依次为:101、103、108、108、110、114,
则中位数为:108,众数为:108;
(2)a==105;
(3)设期中考试所占权重是x,期末考试所占权重是y,
由题意得,
解得:.
答:期中考试所占权重是30%,期末考试所占权重是50%.
25.解:(1)∵甲、乙总成绩相同,
∴a=9+4+7+4+6﹣(7+5+7+a+7)=4,
∵===6,
∴=×[(9﹣6)2+(4﹣6)2+(7﹣6)2+(4﹣6)2+(6﹣6)2]=3.6,
=×[(7)2+(56)2+(7﹣6)2+(4﹣6)2+(7﹣6)2]=1.6;
(2)选择乙,
由(1)得==6,即甲、乙两人平均数相等,而=3.6,=1.6,即甲的方差大于乙的方差,
所以甲的成绩波动较大,
所以乙将被选中.
26.解:(1)a=(80+40+70+50+60)﹣(70+50+70+70)=40,
甲同学成绩的极差为80﹣40=40,
故答案为:40,40;
(2)乙同学的成绩平均数为×(70+50+70+40+70)=60,
方差S乙2=[(70﹣60)2+(50﹣60)2+(70﹣60)2+(40﹣60)2+(70﹣60)2]=160;
(3)因为甲乙两位同学的平均数相同,S甲2>S乙2,
所以乙同学的成绩更稳定.
27.解:(1)表中B完全符合的个数为5,
根据表中数据可看出,A、B的平均数相同,而B完全符合要求的件数多,B的成绩好些.
(2)∵=×[3×(19.9﹣20)2+5×(20﹣20)2+(20.1﹣20)2+(20.2﹣20)2]=0.008,,
∴,
∴在平均数相同的情况下,B的波动小,B的成绩更好一些.
(3)从图中折线走势可知,尽管A的成绩前面起伏大,但后来逐渐稳定,误差小,预测A的潜力大,而B比较稳定,潜力小,所以派A去参赛较合适.
1.已知一组数据1,0,3,﹣1,x,2,3的平均数是1,则这组数据的中位数是( )
A.﹣1 B.1 C.3 D.﹣1或者3
2.小林准备选择一个品牌开运动鞋网店.为此他到多个运动场地随机收集了500个人所穿运动鞋的品牌,对于这组数据他最想知道的是( )
A.众数 B.平均数 C.中位数 D.方差
3.有15名学生参加学校举办的“最强大脑”智力竞赛,比赛结束后根据每个学生的成绩计算平均数、中位数、众数、方差,若去掉一个最高分,一个最低分,则一定不会发生变化的是( )
A.平均数 B.中位数 C.众数 D.方差
4.参加第六届京津冀羽毛球冠军挑战赛的一个代表队的年龄分别是49,20,20,25,31,40,46,20,44,25,这组数据的平均数,众数,中位数分别是( )
A.33,21,27 B.32,20,28 C.33,49,27 D.32,21,22
5.数据201,202,198,199,200的方差与极差分别是( )
A.1,4 B.2,2 C.2,4 D.4,2
6.若x1,x2,x3,x4的平均数为4,x5,x6,x7,…,x10的平均数为6,则x1,x2,…,x10的平均数为( )
A.5 B.4.8 C.5.2 D.8
7.某校为了解学生的课外阅读情况,随机抽取了一个班级的学生,对他们一周的读书时间进行了统计,统计数据如表所示:
读书时间(小时) 7 8 9 10 11
学生人数 6 10 9 8 7
关于该班学生一周读书时间的数据有下列说法:
①一周读书时间数据的中位数是9小时;
②一周读书时间数据的众数是8小时;
③一周读书时间数据的平均数是9小时;
④一周读书时间不少于9小时的人数占抽查学生的50%.
其中说法正确的序号是( )
A.①②③ B.①②④ C.②③④ D.①③④
8.已知一组数据a1,a2,a3,a4,a5的方差是S1,另一组数据a1﹣6,a2﹣6,a3﹣6,a4﹣6,a5﹣6的方差是S2,则S1与S2的大小关系是S1 S2(填写“>”“<”或“=”).
9.甲、乙、丙、丁四人进行射击测试,每人测试10次,平均成绩均为9.2环,方差如表所示:则在这四个选手中,成绩最稳定的是 .
选手 甲 乙 丙 丁
方差 0.56 0.60 0.50 0.45
10.下表是某一时段15名乘客过地铁安检口测体温的数据:
体温(℃) 36.4 36.5 36.6 36.7 36.8 36.9 37.0
人数(人) 1 1 3 2 3 4 1
这组数据的中位数是 .
11.如果一组数据1,2,5,a,9的方差是3,则2,4,10,2a,18的方差是 .
12.小明用s2=[(x1﹣6)2+(x2﹣6)2+…+(x10﹣6)2]计算一组数据的方差,那么x1+x2+x3+…+x10= .
13.数学期末总评成绩是将平时、期中和期末的成绩按3:3:4计算,若小红平时、期中和期末的成绩分别是90分、80分、100分,则小红一学期的数学期末总评成绩是 分.
14.小王前三次打靶的成绩如图所示,他第四次打靶的成绩是a环,且这四次成绩的中位数恰好也是众数,则a= .
15.若5个正数a1,a2,a3,a4,a5的平均数是a,则a1,a2,0,a3,a4,a5的平均数是 .
16.若一组数据x1,x2,…,xn的方差为9,则数据2x1+3,2x2+3,…,2xn+3的方差为 .
17.如果把每千克a元的糖果10千克和每千克b元的糖果3千克混合在一起,那么混合后的糖果的售价是每千克 元.
18.已知2,3,5,m,n五个数据的方差是2,那么4,5,7,m+2,n+2五个数据的方差是 .
19.若一组数据3,4,5,x的极差是5,则x= .
20.一组数据2,3,4,x,6的平均数是4,则这组数据的方差是 .
21.下表是随机抽取的某公司部分员工的月收入资料:
月收入/元 20000 18000 8000 5000 4500 3400 3000 2000
人数 1 1 1 2 4 1 8 2
(1)请计算以上样本的平均数和中位数;
(2)甲乙两人分别用样本平均数和中位数来估计推断公司全体员工月收入水平,请你写出甲乙两人的推断结论;
(3)指出谁的推断比较科学合理,能真实地反映公司全体员工月收入水平,并说出另一个人的推断依据不能真实反映公司全体员工月收入水平的原因.
22.杭州市建兰中学开展防疫知识线上竞赛活动,九年级(1)、(2)班各选出5名选手参加竞赛,两个班选出的5名选手的竞赛成绩(满分为100分)如图所示.
(1)求九(1)班的众数和九(2)班的中位数;
(2)计算两个班竞赛成绩的方差,并说明哪个班的成绩较为整齐.
23.某集团旗下有两家酒店A,B,2020年下半年的月营业额统计如下:
[信息一]A,B两家酒店2020年下半年月营业额(单位:百万元)统计图如下
[信息二]A,B两家酒店2020年下半年月营业额的相关数据统计如下:
酒店 平均数 中位数 众数 方差
A 2.5 2.2 2.2 0.73
B 2.3 1.9 △ 0.59
(1)已知A酒店2020年11月份月营业额为3百万元,求A酒店2020年下半年的营业总额;
(2)求B酒店2020年8月份的月营业额,并补全[信息二]中缺失数据;
(3)结合数据分析,2020年下半年A,B两家酒店哪家经营状况较好,请说明理由.
24.小明本学期的数学成绩如表所示:
测验类别 平时成绩1 平时成绩2 平时成绩3 平时成绩4 平时平均数 期中考试 期末考试
成绩 108 103 101 108 a 110 114
(1)六次测试成绩的中位数和众数分别是什么?
(2)请计算出小明该学期的平时成绩平均分a的值;
(3)如果学期的数学总评成绩是根据一定的权重计算所得,其中平时成绩a所占权重为20%,已知小明该学期的总评成绩为111分,请计算出期中考试和期末考试各自所占权重.
25.某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,甲、乙两人射箭成绩统计表如下.
第1次 第2次 第3次 第4次 第5次
甲成绩 9 4 7 4 6
乙成绩 7 5 7 a 7
(1)求a的值和甲、乙的方差;
(2)请你从平均数和方差的角度分析,谁将被选中.
26.甲、乙两位同学5次数学选拔赛的成绩统计如表,他们5次考试的总成绩相同,请同学们完成下列问题:
第1次 第2次 第3次 第4次 第5次
甲成绩 80 40 70 50 60
乙成绩 70 50 70 a 70
(1)统计表中,a= ,甲同学成绩的极差为 ;
(2)小颖计算了甲同学的成绩平均数为60,方差是S甲2=[(80﹣60)2+(40﹣60)2+(70﹣60)2+(50﹣60)2+(60﹣60)2]=200.请你求出乙同学成绩的平均数和方差;
(3)从平均数和方差的角度分析,甲、乙两位同学谁的成绩更稳定.
27.为选派一名学生参加全市实践活动技能竞赛,A,B两位同学在学校实习基地单位时间内现场进行加工直径为20mm的零件的测试,他俩各加工的10个零件的相关数据依次如图表所示(单位mm):
平均数 方差 完全符合要求个数
A 20 0.026 2
B 20 SB2
根据测试得到的有关数据,试解答下列问题:
(1)考虑平均数与完全符合要求的个数,你认为哪个同学的成绩好些?
(2)计算出SB2的大小,考虑平均数与方差,说明谁的成绩好些?
(3)考虑图中折线走势,你认为派谁去参赛较合适?说明你的理由.
参考答案
1.解:∵一组数据1,0,3,﹣1,x,2,3的平均数是1,
∴[1+0+3+(﹣1)+x+2+3]÷7=1,
解得x=﹣1,
∴这组数据按照从小到大排列是:﹣1,﹣1,0,1,2,3,3,
∴这组数据的中位数是1,
故选:B.
2.解:这组数据他最想知道的是众数.
故选:A.
3.解:去掉一个最高分和一个最低分对中位数没有影响.
故选:B.
4.解:这组数据的平均数是:(49+20+20+25+31+40+46+20+44+25)÷10=32(岁),
这组数据出现最多的数是20,所以这组数据的众数是20岁;
把这些数按从小到大的顺序排列为:20,20,20,25,25,31,40,44,46,49,
则这组数据的中位数是:(25+31)÷2=28(岁).
故选:B.
5.解:极差为202﹣198=4,
∵平均数为=200,
∴方差为×[(201﹣200)2+(202﹣200)2+(198﹣200)2+(199﹣200)2+(200﹣200)2]=2,
故选:C.
6.解:由题意可得,
x1,x2,…,x10的平均数为:===5.2,
故选:C.
7.解:这个班级的学生总数是:6+10+9+8+7=40(人),
则该班学生一周读书时间数据的中位数是:(9+9)÷2=9(小时),说法①正确;
众数是:8小时,说法②正确;
平均数是:(7×6+8×10+9×9+10×8+11×7)=9(小时),说法③正确;
一周读书时间不少于9小时的人数占抽查学生的百分比为:×100%=60%,说法④错误.
故选:A.
8.解:根据题意知,数据a1﹣6,a2﹣6,a3﹣6,a4﹣6,a5﹣6是将数据a1,a2,a3,a4,a5分别减去6所得,
所以两组数据的波动幅度相同,
∴S1=S2,
故答案为:=.
9.解:∵0.60>0.56>0.50>0.45,
∴丁的方差最小,
∴成绩最稳定的是丁,
故答案为:丁.
10.解:将这组数据从小到大的顺序排列后,处于中间位置的那个数是36.8℃,那么由中位数的定义可知,这组数据的中位数是36.8℃.
故答案为:36.8℃.
11.解:∵数据1,2,5,a,9的方差是3,
∴2,4,10,2a,18的方差是22×3=12.
故答案为:12.
12.解:由s2=[(x1﹣6)2+(x2﹣6)2+…+(x10﹣6)2]知这10个数据的平均数为6,
所以x1+x2+x3+…+x10=6×10=60,
故答案为:60.
13.解:根据题意得:小红一学期的数学期末总评成绩是=91(分),
故答案为:91.
14.解:由统计图可知,前三次的中位数是8,
∵第四次打靶的成绩是a环,这四次成绩的中位数恰好也是众数,
∴a=8,
故答案为:8.
15.解:∵正数a1,a2,a3,a4,a5的平均数是a,
∴a1+a2+a3+a4+a5=5a,
∴(a1+a2+0+a3+a4+a5)=a;
故答案为:a.
16.解:设一组数据x1,x2…xn的方差S2=9,
则另一组数据2x1+3,2x2+3…2xn+3的S′2=22S2=36,
故答案为:36.
17.解:由题意可得,
混合后的糖果的售价是每千克(元),
故答案为:.
18.解:由题意知,原数据的平均数为,新数据的每一个数都加了2,则平均数变为+2,
则原来的方差S12=[(x1﹣)2+(x2﹣)2+…+(x5﹣)2]=2,
现在的方差S22=[(x1+2﹣﹣2)2+(x2+2﹣﹣2)2+…+(x5+2﹣﹣2)2]
=[(x1﹣)2+(x2﹣)2+…+(x5﹣)2]=2,
所以方差不变.
故答案为2.
19.解:①x是最小的数时,5﹣x=5,
解得x=0,
②x是最大的数时,x﹣3=5,
解得x=8,
所以,x的值为0或8.
故答案为:0或8.
20.解:∵数据2,3,4,x,6的平均数是4,
∴(2+3+4+x+6)÷5=4,
解得:x=5,
∴这组数据的方差是[(2﹣4)2+(3﹣4)2+(4﹣4)2+(5﹣4)2+(6﹣4)2]=2;
故答案为:2.
解:(1)样本平均数为
=5270(元),
将这20名员工的工资从小到大排列,处在中间位置的两个数的平均数为(3400+3000)÷2=3200(元),因此中位数是3200元,
答:平均数为5270元,中位数是3200元;
(2)甲:由样本平均数为5270元,估计全体员工月平均收入大约为5270元,
乙:由样本中位数为3200元,估计全体员工大约有一半的员工月收入超过3200元,有一半的员工月收入不足3200元;
(3)乙的推断比较科学合理.由题意知样本中的20名员工,只有3名员工的月收入在5270元以上,原因是该样本数据极差较大,所以平均数不能真实反映实际情况.
22.解:(1)由图知,九(1)班成绩为80、80、80、90、100,
九(2)班成绩为70、80、85、95、100,
所以九(1)班成绩的众数为80分,九(2)班成绩的中位数为85分;
(2)九(1)班成绩的平均数为=86(分),九(2)班成绩的平均数为=86(分),
∴九(1)班成绩的方差为×[3×(80﹣86)2+(90﹣86)2+(100﹣86)2]=64,
九(2)班成绩的方差为×[(70﹣86)2+(80﹣86)2+(85﹣86)2+(95﹣86)2+(100﹣86)2]=114,
∴九(1)班成绩较为整齐.
23.解:(1)2.5×6=15(百万元),
答:A酒店2020年下半年的营业总额为15百万元;
(2)B酒店下半年的总营业额为2.3×6=13.8(百万元),
因此B酒店8月份的营业额为13.8﹣1.5﹣1.7﹣2.3﹣1.7﹣3.6=3(百万元),
补全条形统计图如图所示:
(3)A酒店的经营状况较好,理由:A酒店经营营业额的平均数、中位数、众数均比B酒店的高.
24.解:(1)六次数据依次为:101、103、108、108、110、114,
则中位数为:108,众数为:108;
(2)a==105;
(3)设期中考试所占权重是x,期末考试所占权重是y,
由题意得,
解得:.
答:期中考试所占权重是30%,期末考试所占权重是50%.
25.解:(1)∵甲、乙总成绩相同,
∴a=9+4+7+4+6﹣(7+5+7+a+7)=4,
∵===6,
∴=×[(9﹣6)2+(4﹣6)2+(7﹣6)2+(4﹣6)2+(6﹣6)2]=3.6,
=×[(7)2+(56)2+(7﹣6)2+(4﹣6)2+(7﹣6)2]=1.6;
(2)选择乙,
由(1)得==6,即甲、乙两人平均数相等,而=3.6,=1.6,即甲的方差大于乙的方差,
所以甲的成绩波动较大,
所以乙将被选中.
26.解:(1)a=(80+40+70+50+60)﹣(70+50+70+70)=40,
甲同学成绩的极差为80﹣40=40,
故答案为:40,40;
(2)乙同学的成绩平均数为×(70+50+70+40+70)=60,
方差S乙2=[(70﹣60)2+(50﹣60)2+(70﹣60)2+(40﹣60)2+(70﹣60)2]=160;
(3)因为甲乙两位同学的平均数相同,S甲2>S乙2,
所以乙同学的成绩更稳定.
27.解:(1)表中B完全符合的个数为5,
根据表中数据可看出,A、B的平均数相同,而B完全符合要求的件数多,B的成绩好些.
(2)∵=×[3×(19.9﹣20)2+5×(20﹣20)2+(20.1﹣20)2+(20.2﹣20)2]=0.008,,
∴,
∴在平均数相同的情况下,B的波动小,B的成绩更好一些.
(3)从图中折线走势可知,尽管A的成绩前面起伏大,但后来逐渐稳定,误差小,预测A的潜力大,而B比较稳定,潜力小,所以派A去参赛较合适.
