20.3课堂学习 学生体质健康测试中的数据分析-2020-2021学年人教版八年级数学下册同步提升训练(Word版含解析)
文档属性
| 名称 | 20.3课堂学习 学生体质健康测试中的数据分析-2020-2021学年人教版八年级数学下册同步提升训练(Word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 119.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-04 00:00:00 | ||
图片预览




文档简介
2021年人教版八年级数学下册《20.3课堂学习 学生体质健康测试中的数据分析》
同步提升训练(附答案)
1.小林准备选择一个品牌开运动鞋网店.为此他到多个运动场地随机收集了500个人所穿运动鞋的品牌,对于这组数据他最想知道的是( )
A.众数 B.平均数 C.中位数 D.方差
2.有7名大学生去同一家大型公司去面试,公司只录取3人,每个人仅知道自己的面试成绩(每个人的面试成绩都不相同),要想让他们知道是否被录取,公司只需要公布他们面试成绩的( )
A.平均数 B.中位数 C.众数 D.方差
3.将一组数据中的每一个数据都加上3,那么所得的新数据组与原数据组相比,没有改变大小的统计量是( )
A.平均数 B.中位数 C.众数 D.方差
4.要判断一个学生的数学考试成绩是否稳定,那么需要知道他最近连续几次数学考试成绩的( )A.平均数 B.中位数 C.众数 D.方差
5.一组数据3,4,4,5,若添加一个数4,则发生变化的统计量是( )
A.平均数 B.众数 C.中位数 D.方差
6.13名同学参加歌咏比赛,他们的预赛成绩各不相同,现取其中前6名参加决赛,小红同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这13名同学成绩的( )A.方差 B.众数 C.平均数 D.中位数
7.期末考试后,办公室里有两位数学老师正在讨论他们班的数学考试成绩,林老师:“我班的学生考得还不错,有一半的学生考79分以上,一半的学生考不到79分.”王老师:“我班大部分的学生都考在80分到85分之间喔.”依照上面两位老师所叙述的话你认为林、王老师所说的话分别针对( )
A.平均数、众数 B.平均数、极差
C.中位数、方差 D.中位数、众数
8.下列说法错误的是( )
A.一组数据的众数,中位数和平均数不可能是同一个数
B.一组数据的平均数既不可能大于,也不可能小于这组数据中的所有数据
C.一组数据的中位数可能与这组数据的任何数据都不相等
D.众数,中位数和平均数从不同角度描述了一组数据的集中趋势
9.为了从甲、乙两名选手中选拔一名参加射击比赛,现对他们进行一次测验,两个人在相同的条件下各射靶10次,为了比较两人的成绩,制作了如下统计表:
平均数 中位数 方差 命中10环的次数
甲 9.5 9.5 3.7 1
乙 9.5 9.6 5.4 2
若想选拔一位成绩稳定的选手参赛,则表中几个数据应该重点关注的是( )
A.中位数 B.平均数 C.方差 D.命中10环的次数
10.已知A样本的数据如下:67,68,68,71,66,64,64,72,B样本的数据恰好是A样本数据每个都加6,则A、B两个样本的下列统计量对应相同的是( )
A.平均数 B.方差 C.中位数 D.众数
11.将一组数据中的每一个数都加上1得到一组新的数据,那么在众数、中位数、平均数、方差这四个统计量中,值保持不变的是 .
12.家鞋店对上周某一品牌女鞋的销售量统计如下:
尺码/厘米 22 22.5 23 23.5 24 24.5
销售量/双 1 2 5 11 7 3
该鞋店决定本周进该品牌女鞋时多进一些尺码为23.5厘米的鞋,则影响鞋店决策的统计量是 .
13.对于一组数据:x1,x2,x3,…,x10,若去掉一个最大值和一个最小值,则下列统计量一定不会发生变化的是 .
①平均数;②中位数;③众数;④方差.
14.平均数、中位数和众数这三个统计量从不同的侧面反映了数据的集中程度,但也有各自的局限性,其中,容易受极端值影响的统计量是 .
15.某鞋厂调查了商场一个月内不同尺码男鞋的销量,在平均数、中位数、众数和方差等数个统计量中,该鞋厂最关注的是 .
16.在某校“我爱我班”班歌比赛中,有11个班级参加了决赛,各班决赛的最终成绩各不相同,参加了决赛的六班班长想知道自己班级能否获得一等奖(根据比赛规则:最终成绩前5名的班级为一等奖),他不仅要知道自己班级的成绩,还要知道参加决赛的11个班级最终成绩的 (从“平均数、众数、中位数、方差”中选择答案)
17.我校某班筹备班级元旦晚会,班长对全班同学爱吃哪几种水果作了民意调查,决定最终买什么水果.他最应该关注的是调查数据中的 .(填平均数或中位数或众数或方差)
18.在体育课上,九年级2名学生各练习10次立定跳远,要判断哪一名学生的成绩比较稳定,通常需要比较这两名学生立定跳远成绩的 .
19.从甲、乙、丙三个厂家生产的同一种产品中各抽取8件,对它们的使用寿命进行跟踪调查,结果如下:(单位:年)
甲:4,6,6,6,8,9,12,13.
乙:3,3,4,7,9,10,11,12.
丙:3,4,5,6,8,8,8,10.
三个厂家在广告中都称该产品的使用寿命是8年.请根据结果判断,厂家在广告中分别运用了平均数、众数、中位数中的哪一种集中趋势的特征数:
甲: ,乙: ,丙: .
20.某校九(1)班分成12小组做50米短跑练习,并且各组将每次的时间都记录下来,每组都跑五次,各组对谁的成绩比较稳定意见不一,如果你是其中的一员,你应该选用的统计量是 .
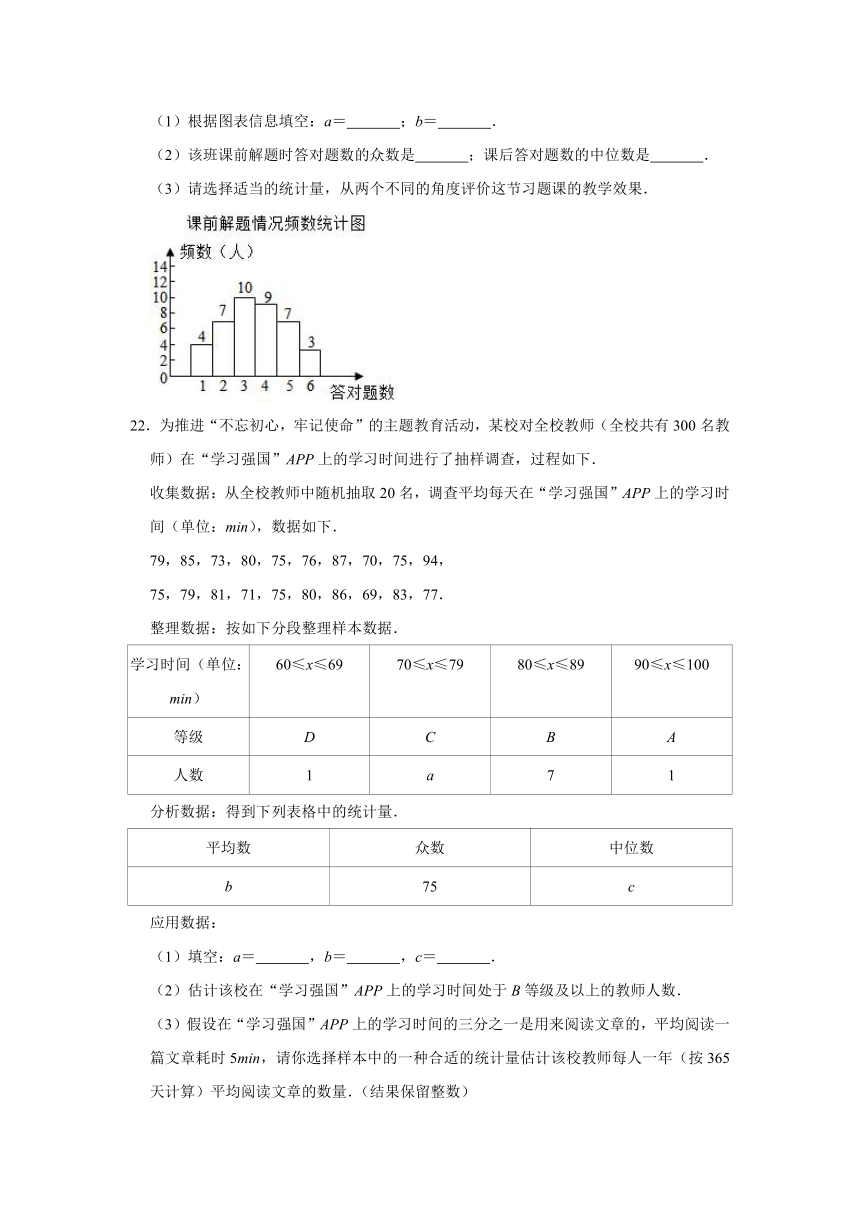
21.线上教学的最大优点是能够依托网络平台及时反馈效果.一次数学习题课课前,陈老师让班上每位同学做6道与这节课内容相关的类似题目,解题情况如图所示.课后,陈老师再让学生做6道类似的题目结果如表所示,已知每位学生至少答对1题.
课后解题情况统计表:
答对题数 频数(人)
1 2
2 3
3 3
4 a
5 9
6 13
合计 b
(1)根据图表信息填空:a= ;b= .
(2)该班课前解题时答对题数的众数是 ;课后答对题数的中位数是 .
(3)请选择适当的统计量,从两个不同的角度评价这节习题课的教学效果.
22.为推进“不忘初心,牢记使命”的主题教育活动,某校对全校教师(全校共有300名教师)在“学习强国”APP上的学习时间进行了抽样调查,过程如下.
收集数据:从全校教师中随机抽取20名,调查平均每天在“学习强国”APP上的学习时间(单位:min),数据如下.
79,85,73,80,75,76,87,70,75,94,
75,79,81,71,75,80,86,69,83,77.
整理数据:按如下分段整理样本数据.
学习时间(单位:min) 60≤x≤69 70≤x≤79 80≤x≤89 90≤x≤100
等级 D C B A
人数 1 a 7 1
分析数据:得到下列表格中的统计量.
平均数 众数 中位数
b 75 c
应用数据:
(1)填空:a= ,b= ,c= .
(2)估计该校在“学习强国”APP上的学习时间处于B等级及以上的教师人数.
(3)假设在“学习强国”APP上的学习时间的三分之一是用来阅读文章的,平均阅读一篇文章耗时5min,请你选择样本中的一种合适的统计量估计该校教师每人一年(按365天计算)平均阅读文章的数量.(结果保留整数)
23.“青年大学习”是共青团中央为组织引导广大青少年,深入学习贯彻习近平新时代中国特色社会主义思想和党的十九大精神的青年学校行动,我校为了解同学某季度学习“青年大学习”的情况,从中随机抽取20位同学,并统计学习时间(学习时间用x表示,单位:分钟)收集数据如下:
30 56 80 30 40 110 120 156 90 120 58 80 120 140 70 84 10 20 100 86
整理数据:按如下分段整理样本数据并补全表格.
课外阅读时间x(min) 0≤x<40 40≤x<80 800≤x<120 120≤x<160
人数 4 a 7 b
分析数据:补全下列表格中的统计量.
平均数 中位数 众数
80 c d
(1)直接写出上述表格中a,b,c,d的值;
(2)我校有1800名同学参加了此次调查活动,请估计学习时间不低于80分钟的人数是多少?
(3)请从中位数和众数中选择一个量,结合本题解释它的意义.
24.国庆长假期间,兴趣小组随机采访了10位到高邮的游客使用“街兔”共享电动车的次数,得到了这10位游客1天内使用“街兔”共享电动车的次数,统计如下:
使用次数 0 2 3 4 6
人数 1 1 4 3 1
(1)这10位游客1天内使用“街兔”共享电动车的次数的中位数是 次,众数是 次,平均数是 次;
(2)若小明同学把统计表中的数据“6”错看成了“5”,则用“街兔”共享电动车的次数的中位数、众数、和平均数这三个统计量中不受影响的是 ;(填“中位数”、“众数”或“平均数”)
(3)若国庆长假期间,每天约有1200位游客到高邮,试估计这些游客7天国庆长假期间使用“街兔”共享电动车的总次数.
25.某区为了了解本区内八年级男生的体能情况,从中随机抽取了40名八年级男生进行“引体向上”个数测试,将测试结果绘制成表格如下:
个数 1 2 3 4 5 6 7 8 9 10 15 21
人数 1 1 6 8 11 4 1 2 2 1 1 2
请根据以上表格信息,解答如下问题:
(1)分析数据,补全表格信息:
平均数 众数 中位数
6
(2)在平均数、中位数和众数中,选择一个你认为比较合适的统计量作为该区八年级男生“引体向上”项目测试的“合格标准”,并说明选择的理由.
(3)如果该区现有8000名八年级男生,根据(2)中选定的“合格标准”,估计该区八年级男生“引体向上”项目测试的合格人数.
26.“新冠肺炎”疫情无疑是对我们每一人的一场生存教育,关注生存环境,就是关注生命.随机抽取某市一年当中若干天的空气质量进行统计分析,其结果如下:
空气质量统计表
污染指数ω 40 70 90 110 130 140
天数(t) 3 5 10 8 3 1
频数分布表
分组 40~60 60~80 80~100 100~120 120~140 合计
频数 3 5 10 8 4
频率
0.167 0.333 0.267 0.133
请仔细观察所给的图表,解答下列问题:
(1)请补全统计图;
(2)如果ω≤100时,空气质量为良;100<ω≤150时,空气质量为轻微污染,估计该城市一年(365天)中有多少天空气质量为轻度污染?
(3)请从平均数、众数及中位数三个特征量中,选择你认为适当的一个特征量对该城市一年空气质量的总体情况进行估计和描述,并说明这种估计的合理性.
参考答案
1.解:这组数据他最想知道的是众数.
故选:A.
2.解:知道自己是否被录取,只需公布第4名的成绩,即中位数.
故选:B.
3.解:将一组数据中的每一个数据都加上3,那么所得的新数据组与原数据组相比波动幅度一致,即两组数据的方差相等,
故选:D.
4.解:方差是衡量波动大小的量,方差越小则波动越小,稳定性也越好.
故选:D.
5.解:原数据的3,4,5,4的平均数为=4,中位数为4,众数为4,方差为×[(3﹣4)2+(4﹣4)2×2+(5﹣4)2]=0.5;
新数据3,4,4,4,5的平均数为=4,中位数为4,众数为4,方差为×[(3﹣4)2+(4﹣4)2×3+(5﹣4)2]=0.4;
所以发生变化的是方差,
故选:D.
6.解:共有13名学生参加比赛,取前6名,所以小红需要知道自己的成绩是否进入前六.
我们把所有同学的成绩按大小顺序排列,第7名学生的成绩是这组数据的中位数,
所以小红知道这组数据的中位数,才能知道自己是否进入决赛.
故选:D.
7.解:∵有一半的学生考79分以上,一半的学生考不到79分,
∴79分是这组数据的中位数,
∵大部分的学生都考在80分到85分之间,
∴众数在此范围内.
故选:D.
8.解:在全部相等的数据中,众数、中位数和平均数是同一个数,故A错;
平均数体现总体的水平,故既不可能大于,也不可能小于这组数据中的所有数据,B正确;
数据为偶数时,中位数与这组数据的任何数据都不相等,C也正确;
众数、中位数和平均数从不同角度描述了一组数据的集中趋势,D也正确.
故选:A.
9.解:∵S甲=3.7<S乙=5.4,
∴应选择甲去参加比赛,
故选:C.
10.解:设样本A中的数据为xi,则样本B中的数据为yi=xi+6,
则样本数据B中的众数和平均数以及中位数和A中的众数,平均数,中位数相差6,
只有方差没有发生变化;
故选:B.
11.解:将一组数据中的每一个数都加上1得到一组新的数据,那么这组数据的波动幅度保持不变,即方差不变,而平均数和众数、中位数均改变.
故答案为:方差.
12.解:鞋店最关心的应该是某一尺码鞋子的销售量最多,在统计量中也就是众数,
所以影响鞋店决策的统计量是众数,
故答案为:众数.
13.解:先去掉一个最大值,去掉一个最小值,再进行统计,则上述四个统计量中,一定不会发生变化的是中位数;
故答案为:②.
14.解:在平均数、中位数和众数这三个统计量中,容易受极端值影响的统计量是平均数;
故答案为:平均数.
15.解:由于众数是数据中出现最多的数,故鞋厂最感兴趣的销售量最多的鞋号即这组数据的众数.
故答案为:众数.
16.解:由题意可得,
11个班级中取前5名,
故只要知道参加决赛的11个班级最终成绩的中位数即可,
故答案为:中位数.
17.解:由于众数是数据中出现次数最多的数,故班长最值得关注的应该是统计调查数据的众数.
故答案为:众数.
18.解:由于方差能反映数据的稳定性,需要比较这2名学生立定跳远成绩的方差.
故答案为:方差.
19.解:(1)甲厂的抽检产品中,平均数为(4+6+6+6+8+9+12+13)÷8=8.75,所以他们选择了平均数8作为他们广告的依据;
乙厂的抽检产品中,中位数是(7+9)÷2=8,所以他们选择了中位数8作为他们广告的依据;
丙厂的抽检产品中,8出现的次数最多,所以他们选择了众数8作为他们广告的依据;
故答案为:平均数,中位数,众数.
20.解:由于方差反映数据的波动情况,应知道数据的方差.
故答案为:方差.
21.解:(1)b=4+7+10+9+7+3=40,
a=40﹣2﹣3﹣3﹣9﹣13=10,
故答案为:10,40;
(2)由频数分布直方图中的数据可知,该班课前解题时答对题数的众数是3题,
由频数分布表中的数据可知课后答对题数的中位数是5题,
故答案为:3题,5题;
(3)课前答对题数的平均数为×(1×4+2×7+3×10+4×9+5×7+6×3)=3.425(题),
课后答对题数的平均数为×(1×2+2×3+3×3+4×10+5×9+6×13)=4.5(题),
从答对题数的平均数知,这节复习课的教学效果明显;
从中位数看,课前答对题数的中位数为3题,课后答对题数的中位数为5题,即课前答对3题及以下的人数有一半以上,而课后有一半以上的人答对5题,这节复习课的教学效果明显.
22.解:(1)11;78.5;78.
解析:a=20﹣1﹣7﹣1=11,
b=(79+85+73+80+75+76+87+70+75+94+75+79+81+71+75+80+86+69+83+77)÷20=78.5,
c=.
故答案为:11;78.5;78.
(2)(名),
答:估计该校在“学习强国”APP上的学习时间处于B等级及以上的教师人数有120名.
(3)(篇).
答:估计该校教师每人一年平均阅读文章的数量为1910篇.
23.解:(1)将数据重新排列为10、20、30、30、56、40、58、70、80、80、84、86、90、100、110、120、120、120、140、156,
∴a=4,b=5,
中位数c==82,众数d=120;
(2)估计学习时间不低于80分钟的人数是1800×=1080(人);
(3)中位数:从中位数看,20名学生中有一半的人数在82分以上;
众数:20名学生中,120分的人数最多.
24.解:(1)这10位游客1天内使用“街兔”共享电动车的次数的中位数是=3(次),众数是3次,平均数为=3.2(次),
故答案为:3、3、3.2;
(2)若小明同学把统计表中的数据“6”错看成了“5”,则用“街兔”共享电动车的次数的中位数、众数、和平均数这三个统计量中不受影响的是中位数和众数,
故答案为:中位数和众数;
(3)估计这些游客7天国庆长假期间使用“街兔”共享电动车的总次数为1200×3.2×7=26880(次).
25.解:(1)∵5个出现了11次,出现的次数最多,
∴众数为5个,
把这些数从小到大排列,中位数是第20、21个数的平均数,
则中位数为=5(个).
故答案为:5,5;
(2)用中位数或众数5个作为合格标准次数较为合适,
因为5个大部分同学都能达到.
(3)根据题意得:
8000×=4800(人).
答:该区八年级男生“引体向上”项目测试的合格人数有4800人.
26.解:(1)图如下面;
分组 40 60 60 80 80 100 100 120 120 140 合计
频数 3 5 10 8 4 30
频率 0.1 0.167 0.333 0.267 0.133 1
(2)估计该城市一年(365年)中有365×0.4=146天空气质量为轻微污染;
(3)该组数据的平均数为(40×3+70×5+90×10+110×8+130×3+140)=92.7,中位数和众数都为90.用中位数或众数来估计质量状况.平均数受极端特异数的影响较大;出现90的天数最多.
同步提升训练(附答案)
1.小林准备选择一个品牌开运动鞋网店.为此他到多个运动场地随机收集了500个人所穿运动鞋的品牌,对于这组数据他最想知道的是( )
A.众数 B.平均数 C.中位数 D.方差
2.有7名大学生去同一家大型公司去面试,公司只录取3人,每个人仅知道自己的面试成绩(每个人的面试成绩都不相同),要想让他们知道是否被录取,公司只需要公布他们面试成绩的( )
A.平均数 B.中位数 C.众数 D.方差
3.将一组数据中的每一个数据都加上3,那么所得的新数据组与原数据组相比,没有改变大小的统计量是( )
A.平均数 B.中位数 C.众数 D.方差
4.要判断一个学生的数学考试成绩是否稳定,那么需要知道他最近连续几次数学考试成绩的( )A.平均数 B.中位数 C.众数 D.方差
5.一组数据3,4,4,5,若添加一个数4,则发生变化的统计量是( )
A.平均数 B.众数 C.中位数 D.方差
6.13名同学参加歌咏比赛,他们的预赛成绩各不相同,现取其中前6名参加决赛,小红同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这13名同学成绩的( )A.方差 B.众数 C.平均数 D.中位数
7.期末考试后,办公室里有两位数学老师正在讨论他们班的数学考试成绩,林老师:“我班的学生考得还不错,有一半的学生考79分以上,一半的学生考不到79分.”王老师:“我班大部分的学生都考在80分到85分之间喔.”依照上面两位老师所叙述的话你认为林、王老师所说的话分别针对( )
A.平均数、众数 B.平均数、极差
C.中位数、方差 D.中位数、众数
8.下列说法错误的是( )
A.一组数据的众数,中位数和平均数不可能是同一个数
B.一组数据的平均数既不可能大于,也不可能小于这组数据中的所有数据
C.一组数据的中位数可能与这组数据的任何数据都不相等
D.众数,中位数和平均数从不同角度描述了一组数据的集中趋势
9.为了从甲、乙两名选手中选拔一名参加射击比赛,现对他们进行一次测验,两个人在相同的条件下各射靶10次,为了比较两人的成绩,制作了如下统计表:
平均数 中位数 方差 命中10环的次数
甲 9.5 9.5 3.7 1
乙 9.5 9.6 5.4 2
若想选拔一位成绩稳定的选手参赛,则表中几个数据应该重点关注的是( )
A.中位数 B.平均数 C.方差 D.命中10环的次数
10.已知A样本的数据如下:67,68,68,71,66,64,64,72,B样本的数据恰好是A样本数据每个都加6,则A、B两个样本的下列统计量对应相同的是( )
A.平均数 B.方差 C.中位数 D.众数
11.将一组数据中的每一个数都加上1得到一组新的数据,那么在众数、中位数、平均数、方差这四个统计量中,值保持不变的是 .
12.家鞋店对上周某一品牌女鞋的销售量统计如下:
尺码/厘米 22 22.5 23 23.5 24 24.5
销售量/双 1 2 5 11 7 3
该鞋店决定本周进该品牌女鞋时多进一些尺码为23.5厘米的鞋,则影响鞋店决策的统计量是 .
13.对于一组数据:x1,x2,x3,…,x10,若去掉一个最大值和一个最小值,则下列统计量一定不会发生变化的是 .
①平均数;②中位数;③众数;④方差.
14.平均数、中位数和众数这三个统计量从不同的侧面反映了数据的集中程度,但也有各自的局限性,其中,容易受极端值影响的统计量是 .
15.某鞋厂调查了商场一个月内不同尺码男鞋的销量,在平均数、中位数、众数和方差等数个统计量中,该鞋厂最关注的是 .
16.在某校“我爱我班”班歌比赛中,有11个班级参加了决赛,各班决赛的最终成绩各不相同,参加了决赛的六班班长想知道自己班级能否获得一等奖(根据比赛规则:最终成绩前5名的班级为一等奖),他不仅要知道自己班级的成绩,还要知道参加决赛的11个班级最终成绩的 (从“平均数、众数、中位数、方差”中选择答案)
17.我校某班筹备班级元旦晚会,班长对全班同学爱吃哪几种水果作了民意调查,决定最终买什么水果.他最应该关注的是调查数据中的 .(填平均数或中位数或众数或方差)
18.在体育课上,九年级2名学生各练习10次立定跳远,要判断哪一名学生的成绩比较稳定,通常需要比较这两名学生立定跳远成绩的 .
19.从甲、乙、丙三个厂家生产的同一种产品中各抽取8件,对它们的使用寿命进行跟踪调查,结果如下:(单位:年)
甲:4,6,6,6,8,9,12,13.
乙:3,3,4,7,9,10,11,12.
丙:3,4,5,6,8,8,8,10.
三个厂家在广告中都称该产品的使用寿命是8年.请根据结果判断,厂家在广告中分别运用了平均数、众数、中位数中的哪一种集中趋势的特征数:
甲: ,乙: ,丙: .
20.某校九(1)班分成12小组做50米短跑练习,并且各组将每次的时间都记录下来,每组都跑五次,各组对谁的成绩比较稳定意见不一,如果你是其中的一员,你应该选用的统计量是 .
21.线上教学的最大优点是能够依托网络平台及时反馈效果.一次数学习题课课前,陈老师让班上每位同学做6道与这节课内容相关的类似题目,解题情况如图所示.课后,陈老师再让学生做6道类似的题目结果如表所示,已知每位学生至少答对1题.
课后解题情况统计表:
答对题数 频数(人)
1 2
2 3
3 3
4 a
5 9
6 13
合计 b
(1)根据图表信息填空:a= ;b= .
(2)该班课前解题时答对题数的众数是 ;课后答对题数的中位数是 .
(3)请选择适当的统计量,从两个不同的角度评价这节习题课的教学效果.
22.为推进“不忘初心,牢记使命”的主题教育活动,某校对全校教师(全校共有300名教师)在“学习强国”APP上的学习时间进行了抽样调查,过程如下.
收集数据:从全校教师中随机抽取20名,调查平均每天在“学习强国”APP上的学习时间(单位:min),数据如下.
79,85,73,80,75,76,87,70,75,94,
75,79,81,71,75,80,86,69,83,77.
整理数据:按如下分段整理样本数据.
学习时间(单位:min) 60≤x≤69 70≤x≤79 80≤x≤89 90≤x≤100
等级 D C B A
人数 1 a 7 1
分析数据:得到下列表格中的统计量.
平均数 众数 中位数
b 75 c
应用数据:
(1)填空:a= ,b= ,c= .
(2)估计该校在“学习强国”APP上的学习时间处于B等级及以上的教师人数.
(3)假设在“学习强国”APP上的学习时间的三分之一是用来阅读文章的,平均阅读一篇文章耗时5min,请你选择样本中的一种合适的统计量估计该校教师每人一年(按365天计算)平均阅读文章的数量.(结果保留整数)
23.“青年大学习”是共青团中央为组织引导广大青少年,深入学习贯彻习近平新时代中国特色社会主义思想和党的十九大精神的青年学校行动,我校为了解同学某季度学习“青年大学习”的情况,从中随机抽取20位同学,并统计学习时间(学习时间用x表示,单位:分钟)收集数据如下:
30 56 80 30 40 110 120 156 90 120 58 80 120 140 70 84 10 20 100 86
整理数据:按如下分段整理样本数据并补全表格.
课外阅读时间x(min) 0≤x<40 40≤x<80 800≤x<120 120≤x<160
人数 4 a 7 b
分析数据:补全下列表格中的统计量.
平均数 中位数 众数
80 c d
(1)直接写出上述表格中a,b,c,d的值;
(2)我校有1800名同学参加了此次调查活动,请估计学习时间不低于80分钟的人数是多少?
(3)请从中位数和众数中选择一个量,结合本题解释它的意义.
24.国庆长假期间,兴趣小组随机采访了10位到高邮的游客使用“街兔”共享电动车的次数,得到了这10位游客1天内使用“街兔”共享电动车的次数,统计如下:
使用次数 0 2 3 4 6
人数 1 1 4 3 1
(1)这10位游客1天内使用“街兔”共享电动车的次数的中位数是 次,众数是 次,平均数是 次;
(2)若小明同学把统计表中的数据“6”错看成了“5”,则用“街兔”共享电动车的次数的中位数、众数、和平均数这三个统计量中不受影响的是 ;(填“中位数”、“众数”或“平均数”)
(3)若国庆长假期间,每天约有1200位游客到高邮,试估计这些游客7天国庆长假期间使用“街兔”共享电动车的总次数.
25.某区为了了解本区内八年级男生的体能情况,从中随机抽取了40名八年级男生进行“引体向上”个数测试,将测试结果绘制成表格如下:
个数 1 2 3 4 5 6 7 8 9 10 15 21
人数 1 1 6 8 11 4 1 2 2 1 1 2
请根据以上表格信息,解答如下问题:
(1)分析数据,补全表格信息:
平均数 众数 中位数
6
(2)在平均数、中位数和众数中,选择一个你认为比较合适的统计量作为该区八年级男生“引体向上”项目测试的“合格标准”,并说明选择的理由.
(3)如果该区现有8000名八年级男生,根据(2)中选定的“合格标准”,估计该区八年级男生“引体向上”项目测试的合格人数.
26.“新冠肺炎”疫情无疑是对我们每一人的一场生存教育,关注生存环境,就是关注生命.随机抽取某市一年当中若干天的空气质量进行统计分析,其结果如下:
空气质量统计表
污染指数ω 40 70 90 110 130 140
天数(t) 3 5 10 8 3 1
频数分布表
分组 40~60 60~80 80~100 100~120 120~140 合计
频数 3 5 10 8 4
频率
0.167 0.333 0.267 0.133
请仔细观察所给的图表,解答下列问题:
(1)请补全统计图;
(2)如果ω≤100时,空气质量为良;100<ω≤150时,空气质量为轻微污染,估计该城市一年(365天)中有多少天空气质量为轻度污染?
(3)请从平均数、众数及中位数三个特征量中,选择你认为适当的一个特征量对该城市一年空气质量的总体情况进行估计和描述,并说明这种估计的合理性.
参考答案
1.解:这组数据他最想知道的是众数.
故选:A.
2.解:知道自己是否被录取,只需公布第4名的成绩,即中位数.
故选:B.
3.解:将一组数据中的每一个数据都加上3,那么所得的新数据组与原数据组相比波动幅度一致,即两组数据的方差相等,
故选:D.
4.解:方差是衡量波动大小的量,方差越小则波动越小,稳定性也越好.
故选:D.
5.解:原数据的3,4,5,4的平均数为=4,中位数为4,众数为4,方差为×[(3﹣4)2+(4﹣4)2×2+(5﹣4)2]=0.5;
新数据3,4,4,4,5的平均数为=4,中位数为4,众数为4,方差为×[(3﹣4)2+(4﹣4)2×3+(5﹣4)2]=0.4;
所以发生变化的是方差,
故选:D.
6.解:共有13名学生参加比赛,取前6名,所以小红需要知道自己的成绩是否进入前六.
我们把所有同学的成绩按大小顺序排列,第7名学生的成绩是这组数据的中位数,
所以小红知道这组数据的中位数,才能知道自己是否进入决赛.
故选:D.
7.解:∵有一半的学生考79分以上,一半的学生考不到79分,
∴79分是这组数据的中位数,
∵大部分的学生都考在80分到85分之间,
∴众数在此范围内.
故选:D.
8.解:在全部相等的数据中,众数、中位数和平均数是同一个数,故A错;
平均数体现总体的水平,故既不可能大于,也不可能小于这组数据中的所有数据,B正确;
数据为偶数时,中位数与这组数据的任何数据都不相等,C也正确;
众数、中位数和平均数从不同角度描述了一组数据的集中趋势,D也正确.
故选:A.
9.解:∵S甲=3.7<S乙=5.4,
∴应选择甲去参加比赛,
故选:C.
10.解:设样本A中的数据为xi,则样本B中的数据为yi=xi+6,
则样本数据B中的众数和平均数以及中位数和A中的众数,平均数,中位数相差6,
只有方差没有发生变化;
故选:B.
11.解:将一组数据中的每一个数都加上1得到一组新的数据,那么这组数据的波动幅度保持不变,即方差不变,而平均数和众数、中位数均改变.
故答案为:方差.
12.解:鞋店最关心的应该是某一尺码鞋子的销售量最多,在统计量中也就是众数,
所以影响鞋店决策的统计量是众数,
故答案为:众数.
13.解:先去掉一个最大值,去掉一个最小值,再进行统计,则上述四个统计量中,一定不会发生变化的是中位数;
故答案为:②.
14.解:在平均数、中位数和众数这三个统计量中,容易受极端值影响的统计量是平均数;
故答案为:平均数.
15.解:由于众数是数据中出现最多的数,故鞋厂最感兴趣的销售量最多的鞋号即这组数据的众数.
故答案为:众数.
16.解:由题意可得,
11个班级中取前5名,
故只要知道参加决赛的11个班级最终成绩的中位数即可,
故答案为:中位数.
17.解:由于众数是数据中出现次数最多的数,故班长最值得关注的应该是统计调查数据的众数.
故答案为:众数.
18.解:由于方差能反映数据的稳定性,需要比较这2名学生立定跳远成绩的方差.
故答案为:方差.
19.解:(1)甲厂的抽检产品中,平均数为(4+6+6+6+8+9+12+13)÷8=8.75,所以他们选择了平均数8作为他们广告的依据;
乙厂的抽检产品中,中位数是(7+9)÷2=8,所以他们选择了中位数8作为他们广告的依据;
丙厂的抽检产品中,8出现的次数最多,所以他们选择了众数8作为他们广告的依据;
故答案为:平均数,中位数,众数.
20.解:由于方差反映数据的波动情况,应知道数据的方差.
故答案为:方差.
21.解:(1)b=4+7+10+9+7+3=40,
a=40﹣2﹣3﹣3﹣9﹣13=10,
故答案为:10,40;
(2)由频数分布直方图中的数据可知,该班课前解题时答对题数的众数是3题,
由频数分布表中的数据可知课后答对题数的中位数是5题,
故答案为:3题,5题;
(3)课前答对题数的平均数为×(1×4+2×7+3×10+4×9+5×7+6×3)=3.425(题),
课后答对题数的平均数为×(1×2+2×3+3×3+4×10+5×9+6×13)=4.5(题),
从答对题数的平均数知,这节复习课的教学效果明显;
从中位数看,课前答对题数的中位数为3题,课后答对题数的中位数为5题,即课前答对3题及以下的人数有一半以上,而课后有一半以上的人答对5题,这节复习课的教学效果明显.
22.解:(1)11;78.5;78.
解析:a=20﹣1﹣7﹣1=11,
b=(79+85+73+80+75+76+87+70+75+94+75+79+81+71+75+80+86+69+83+77)÷20=78.5,
c=.
故答案为:11;78.5;78.
(2)(名),
答:估计该校在“学习强国”APP上的学习时间处于B等级及以上的教师人数有120名.
(3)(篇).
答:估计该校教师每人一年平均阅读文章的数量为1910篇.
23.解:(1)将数据重新排列为10、20、30、30、56、40、58、70、80、80、84、86、90、100、110、120、120、120、140、156,
∴a=4,b=5,
中位数c==82,众数d=120;
(2)估计学习时间不低于80分钟的人数是1800×=1080(人);
(3)中位数:从中位数看,20名学生中有一半的人数在82分以上;
众数:20名学生中,120分的人数最多.
24.解:(1)这10位游客1天内使用“街兔”共享电动车的次数的中位数是=3(次),众数是3次,平均数为=3.2(次),
故答案为:3、3、3.2;
(2)若小明同学把统计表中的数据“6”错看成了“5”,则用“街兔”共享电动车的次数的中位数、众数、和平均数这三个统计量中不受影响的是中位数和众数,
故答案为:中位数和众数;
(3)估计这些游客7天国庆长假期间使用“街兔”共享电动车的总次数为1200×3.2×7=26880(次).
25.解:(1)∵5个出现了11次,出现的次数最多,
∴众数为5个,
把这些数从小到大排列,中位数是第20、21个数的平均数,
则中位数为=5(个).
故答案为:5,5;
(2)用中位数或众数5个作为合格标准次数较为合适,
因为5个大部分同学都能达到.
(3)根据题意得:
8000×=4800(人).
答:该区八年级男生“引体向上”项目测试的合格人数有4800人.
26.解:(1)图如下面;
分组 40 60 60 80 80 100 100 120 120 140 合计
频数 3 5 10 8 4 30
频率 0.1 0.167 0.333 0.267 0.133 1
(2)估计该城市一年(365年)中有365×0.4=146天空气质量为轻微污染;
(3)该组数据的平均数为(40×3+70×5+90×10+110×8+130×3+140)=92.7,中位数和众数都为90.用中位数或众数来估计质量状况.平均数受极端特异数的影响较大;出现90的天数最多.
