【单元测评培优卷】第10章 数据的收集、整理与描述(原版+解析版)
文档属性
| 名称 | 【单元测评培优卷】第10章 数据的收集、整理与描述(原版+解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-03 15:05:54 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2020-2021学年浙教版七年级下册数学
单元测评培优卷(原版+解析版)
第10章
数据的收集、整理与描述
(测试时间:120分钟,满分:120分)
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2021·福建省福州第一中学七年级期中)下列调查中,调查方式选择合理的是(
)
A.为了了解某一批灯泡的寿命,选择全面调查
B.为了了解一批袋装食品是否含有防腐剂,选择全面调查
C.为了了解“天问一号”的设备零件的质量情况,选择抽样调查
D.为了了解某年福州市的空气质量,选择抽样调查
2.(2020春?高新区期中)今年某校有2000名学生参加线上学习,为了解这些学生的数学成绩,从中抽取100名考生的数学成绩进行统计分析,以下说法正确的是( )
A.2000名学生是总体
B.每位学生的数学成绩是个体
C.这100名学生是总体的一个样本
D.100名学生是样本容量
3.(2021·湖南常德市·七年级期末)为了准确反映某车队8名司机6月份耗去的汽油费用,且便于比较,那么选用最合适、直观的统计图是(
)
A.折线统计图
B.扇形统计图
C.条形统计图
D.统计表
4.(2020秋?南关区校级期中)我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1500石,验得米内夹谷,抽样取米一把,数得250粒内夹谷30粒.则这批米内夹谷约为( )
A.140石
B.160石
C.180石
D.200石
5.(2020·北京)北京市实施垃圾分类以来,为了调动居民参与垃圾分类的积极性,某社区实行垃圾分类积分兑换奖品活动.随机抽取了若干户5月份的积分情况,并对抽取的样本进行了整理得到下列不完整的统计表:
积分x/分
频数
频率
0≤x<50
4
0.1
50≤x<100
8
0.2
100≤x<200
16
b
x≥200
a
0.3
根据以上信息可得( )
A.a=40,b=0.4
B.a=12,b=0.4
C.a=10,b=0.5
D.a=4,b=0.5
6.(2020·北京市三帆中学初三期中)为加强锻炼增强体魄,我校初三(1)班同学组建了足球、篮球、乒乓球、跳绳四个体育活动小组.经调查,全班同学全员参与各活动小组人数分布情况的扇形图和条形图如图所示:①该班有50名学生;②篮球有16人;③跳绳人数所占扇形圆心角为57.6°;④足球人数所占扇形圆心角为120°。这四种说法中正确的有( )
A.2个
B.0个
C.1个
D.3个
7.(2021·安徽九年级专题练习)某城市经济生产总值最近4年的增长情况如图所示,请判断下列说法中正确的为(
)
A.2013年到2016年该城市的经济生产总值不变
B.2013年到2016年该城市的经济生产总值一直在下降
C.2013年到2016年该城市的经济生产总值有升有降
D.2013年到2016年该城市的经济生产总值一直在上升
8.(2020春?南岗区校级期中)一个容量为80的样本,最大值为50,最小值为9,取组距为10,则可以分成( )
A.4组
B.5组
C.9组
D.10组
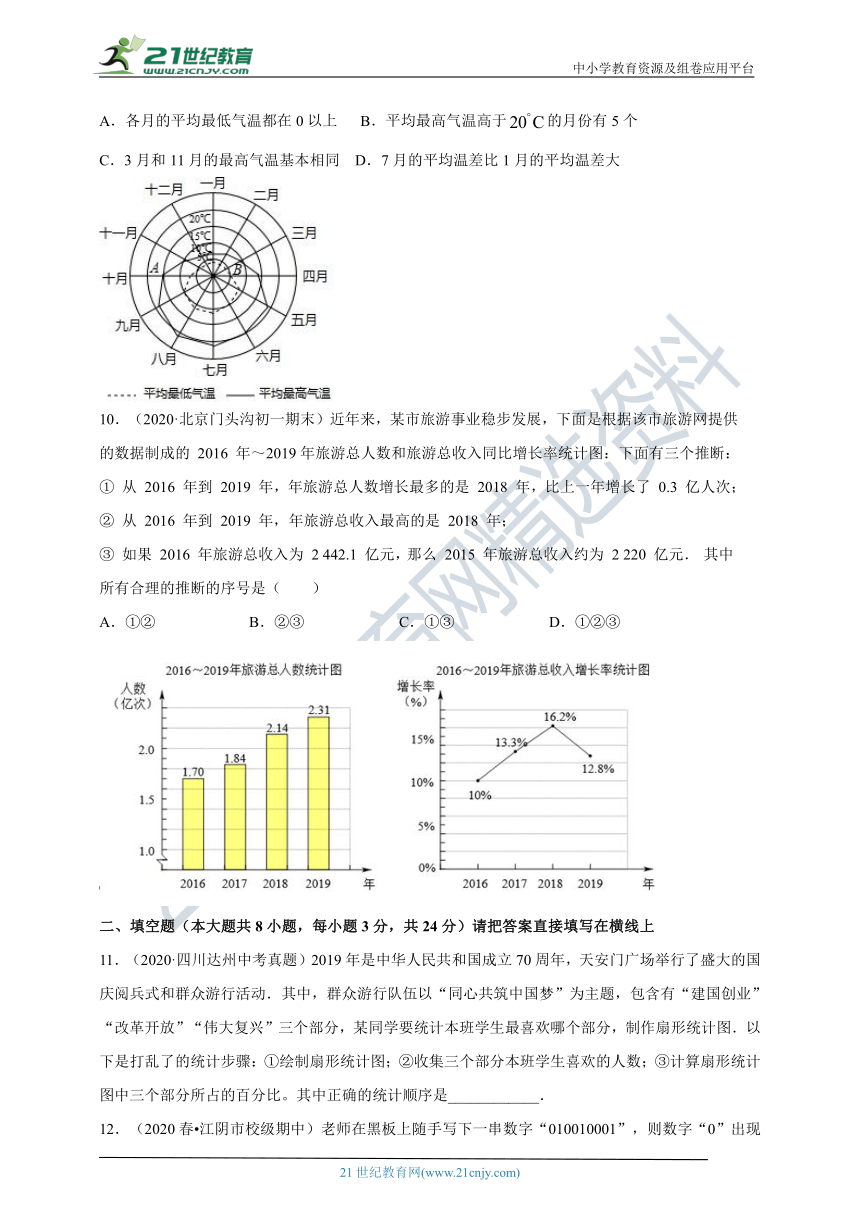
9.(2020·北京九年级专题练习)某旅游城市为向游客介绍本地的气温情况,绘制了一年中12个月平均最高气温和平均最低气温的雷达图,图中点表示10月的平均最高气温约为,点表示4月的平均最低气温约为,下面叙述不正确的是(
)
A.各月的平均最低气温都在0以上
B.平均最高气温高于的月份有5个
C.3月和11月的最高气温基本相同
D.7月的平均温差比1月的平均温差大
10.(2020·北京门头沟初一期末)近年来,某市旅游事业稳步发展,下面是根据该市旅游网提供的数据制成的
2016
年~2019年旅游总人数和旅游总收入同比增长率统计图:下面有三个推断:
①
从
2016
年到
2019
年,年旅游总人数增长最多的是
2018
年,比上一年增长了
0.3
亿人次;
②
从
2016
年到
2019
年,年旅游总收入最高的是
2018
年;
③
如果
2016
年旅游总收入为
2
442.1
亿元,那么
2015
年旅游总收入约为
2
220
亿元.
其中所有合理的推断的序号是(
)
A.①②
B.②③
C.①③
D.①②③
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020·四川达州中考真题)2019年是中华人民共和国成立70周年,天安门广场举行了盛大的国庆阅兵式和群众游行活动.其中,群众游行队伍以“同心共筑中国梦”为主题,包含有“建国创业”“改革开放”“伟大复兴”三个部分,某同学要统计本班学生最喜欢哪个部分,制作扇形统计图.以下是打乱了的统计步骤:①绘制扇形统计图;②收集三个部分本班学生喜欢的人数;③计算扇形统计图中三个部分所占的百分比。其中正确的统计顺序是____________.
12.(2020春?江阴市校级期中)老师在黑板上随手写下一串数字“010010001”,则数字“0”出现的频率是 .
13.(2020春?西城区校级期中)当前,“低头族”已成为热门话题之一,为了了解路边行人边走路边低头看手机的情况,应采用的收集数据的方式是
;
A.对学校的同学发放问卷进行调查B.对在路边行走的学生随机发放问卷进行调查
C.对在图书馆里看书的人发放问卷进行调查D.对在路边行走的路人随机发放问卷进行调查
并说出你的理由
.
14.(2020秋?永安市期中)为了估计池塘里有多少条鱼,我们从池塘里捕上100条做上标记,然后放回池塘里,经过一段时间待带标记的鱼完全混合于鱼群中后,第二次捕得200条,发现其中带标记的鱼25条,通过这种调查方式,我们可以估计出这个池塘里有
条鱼.
15.(2020春?句容市期中)将某班男生的身高分成了三组,情况如表所示,则表中b的值是 30% .
第一组
第二组
第三组
频数
6
10
a
频率
b
c
20%
16.(2021·北京四中七年级期中)在1~7月份,某种水果的每斤进价与每斤售价的信息如图所示,则出售该种水果每斤利润最大的月份是_____月份.
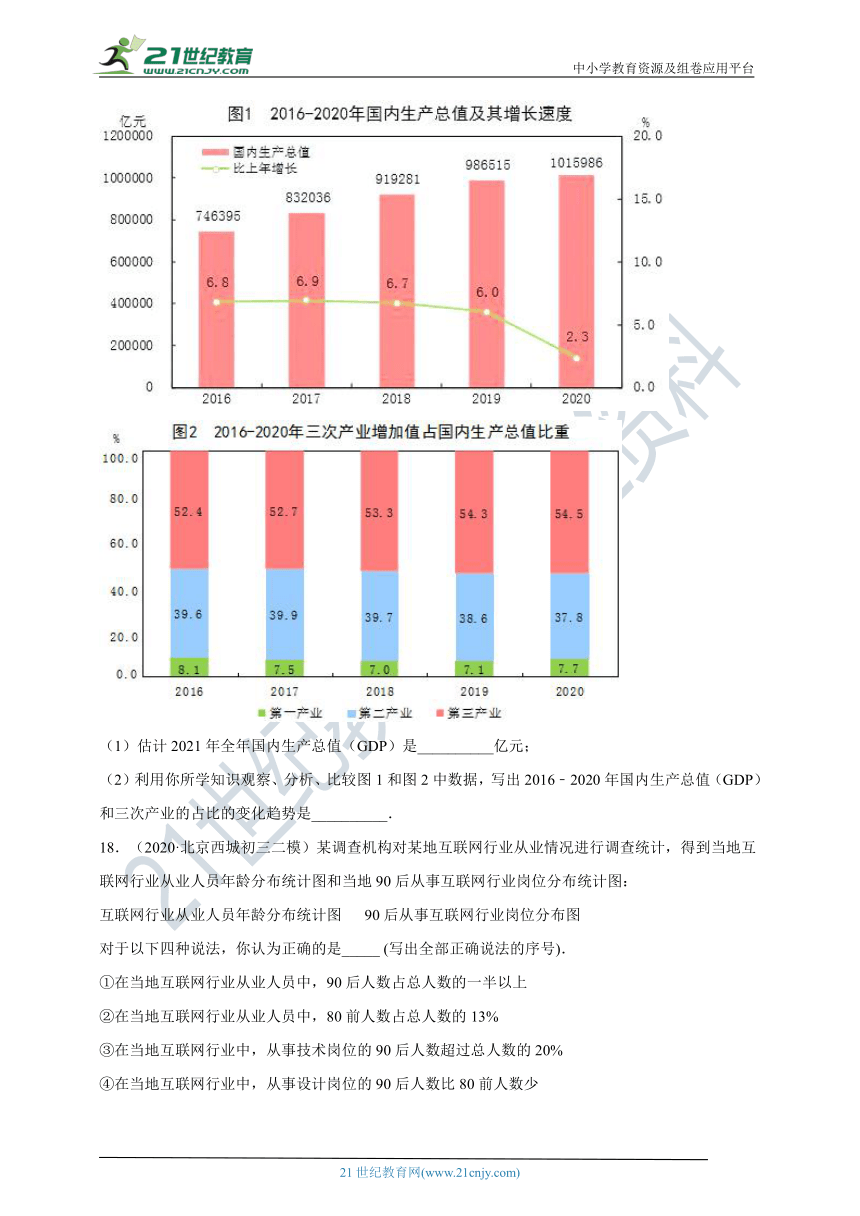
17.(2021·北京九年级一模)在国家统计局发布的我国2020年国民经济和社会发展统计公报中,给出了统计图1和图2.
(1)估计2021年全年国内生产总值(GDP)是__________亿元;
(2)利用你所学知识观察、分析、比较图1和图2中数据,写出2016﹣2020年国内生产总值(GDP)和三次产业的占比的变化趋势是__________.
18.(2020·北京西城初三二模)某调查机构对某地互联网行业从业情况进行调查统计,得到当地互联网行业从业人员年龄分布统计图和当地90后从事互联网行业岗位分布统计图:
互联网行业从业人员年龄分布统计图
90后从事互联网行业岗位分布图
对于以下四种说法,你认为正确的是_____
(写出全部正确说法的序号).
①在当地互联网行业从业人员中,90后人数占总人数的一半以上
②在当地互联网行业从业人员中,80前人数占总人数的13%
③在当地互联网行业中,从事技术岗位的90后人数超过总人数的20%
④在当地互联网行业中,从事设计岗位的90后人数比80前人数少
三、解答题(本大题共7小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020秋?增城区期末)根据电力部门统计,每天8:00至21:00是用电的高峰期,简称“峰时”,21:00至次日8:00是用电的低谷时期,简称“谷时”.为了缓解供电需求紧张的矛盾,某市电力部门于2020年10月统一换装“峰谷分时”电表,对用电实行“峰谷分时电价”新政策,具体见表:
时间
换表前
换表后
电价
每度0.52元
峰时(8:00~21:00)
谷时(21:00~次日8:00)
每度0.55元
每度0.30元
(1)若小王家9月份(换表前)的用电量为80度,则该月电费为
元;
(2)小张家11月份“峰时”用电50度,“谷时”用电20度,问小张家11月份的电费是多少元?
(3)小李家12月份用电95度,经测算比换表前使用95度电节省了5.9元,问小李家12月份使用“峰时电”和“谷时电”分别是多少度?
20.(2020秋?历城区期末)小强是校学生会体育部部长,他想了解现在同学们更喜欢什么球类运动,以便学生会组织比赛,小强随机调查了300名同学,调在结果如下表:
最喜欢的球类运动
篮球
足球
排球
乒乓球
羽毛球
其他
人数
68
m
27
90
36
9
(1)本次调查结果中喜欢足球运动项目的人数m= ;
(2)本次调查结果中喜欢排球运动项目的人数占调查总人数的百分比是 ;
(3)根据调查数据,在绘制扇形统计图的过程中,羽毛球所对应扇形的圆心角度数等于 °;
(4)如果你是体育部长,根据调查的结果,你会组织什么比赛?说说你的理由.
21.(2021·河南南阳市·九年级一模)2020年国家提出并部署了“新基建”项目,主要包含“特高压,城际高速铁路和城市轨道交通,5G基站建设,工业互联网,大数据中心,人工智能,新能源汽车充电桩”等.《2020新基建中高端人才市场就业吸引力报告》重点刻画了“新基建”中五大细分领域(5G基站建设,工业互联网,大数据中心,人工智能,新能源汽车充电桩)总体的人才与就业机会.下图是其中的一个统计图.
请根据图中信息,解答下列问题:
(1)图中2020年“新基建”七大领域预计投资规模的平均数约是________亿元(结果保留一位小数);
(2)在由“新基建”七大领域预计投资规模组成的扇形统计图中,“新能源汽车充电桩”预计投资规模所占的圆心角约是_______(结果保留整数);(3)甲,乙两位待业人员,仅根据上面统计图中的数据,从五大细分领域中,甲选择了“5G基站建设”,乙选择了“人工智能”分别作为自己的就业方向,请简要说明他们选择就业方向的理由各是什么.
22.(2020·北京大兴初三一模)新冠肺炎疫情暴发后,一场同时间赛跑、与病魔较量的战役随即打响.在疫情防控一线,除了广大医务工作者义无反顾、日夜奋战之外,在另一条战线上,科研人员也在加班加点、紧急攻关.全国科技战线积极响应党中央号召,科技、卫健等12个部门组成科研攻关组,短短一个月的时间内就取得了积极进展.3月13日0﹣24时,31个省(自治区、直辖市)和新疆生产建设兵团新增确诊病例11例(数据不含港澳台),新增疑似病例17例(数据不含港澳台).如图是根据国家卫健委关于新型冠状病毒肺炎通报的数据(数据不含港澳台)绘制的统计图:
根据以上信息,回答下列问题:
(1)下列推断合理的是_______.
①2月15日武汉新增确诊病例约为1500例;②从2月23日起到3月13日止,武汉每日新增确诊病例都在500例以下;③从2月23日起到3月13日止,全国每日新增疑似病例逐渐减少.④3月13日湖北新增疑似病例不超过17例.
(2)结合本题的信息及当前防疫形势,说说你的感受.
23.(2020·北京通州初三一模)国务院发布的《全民科学素质行动计划纲要实施方案(2016-2020年)》指出:公民科学素质是实施创新驱动发展战略的基础,是国家综合国力的体现.《方案》明确提出,2020年要将我国公民科学素质的数值提升到10%以上.为了解我国公民科学素质水平及发展状况,中国科协等单位已多次组织了全国范围的调查,以下是根据调查结果整理得到的部分信息.注:科学素质的数值是指具备一定科学素质的公民人数占公民总数的百分比.
.2015和2018年我国各直辖市公民科学素质发展状况统计图如下:
2015年
2018年
男
女
b.2015年和2018年我国公民科学素质发展状况按性别分类统计如下:
c.2001年以来我国公民科学素质水平发展统计图如下:
根据以上信息,回答下列问题:
(1)在我国四个直辖市中,从2015年到2018年,公民科学素质水平增幅最大的城市是________,公民科学素质水平增速最快的城市是_________.注:科学素质水平增幅=2018年科学素质的数值一2015年科学素质的数值;科学素质水平增速=(2018年科学素质的数值一2015年科学素质的数值)÷2015年科学素质的数值.
(2)已知在2015年的调查样本中,男女公民的比例约为1:1,则2015年我国公民的科学素质水平为______%(结果保留一位小数);由计算可知.在2018年的调查样本中.男性公民人数_____女性公民人数(填“多于”、“等于”或“少于”).(3)根据截至2018年的调查数据推断,你认为“2020年我国公民科学素质提升到10%以上”的目标能够实现吗?请说明理由.
24.(2019·浙江江干初二期末)为了节约能源,某城市开展了节约水电活动,已知该城市共有10000户家庭,活动前,某调查小组随机抽取了部分家庭每月的水电费的开支(单位:元),结果如左图所示频数直方图(每一组含前一个边界值,不含后一个边界值);活动后,再次调查这些家庭每月的水电费的开支,结果如表所示:
(1)求所抽取的样本的容量;(2)如以每月水电费开支在225元以下(不含)为达到节约标准,请问通过本次活动,该城市大约增加了多少户家庭达到节约标准?(3)活动后,这些样本家庭每月水电费开支的总额能否低于6000元?(4)请选择一个适当的统计量分析活动前后的相关数据,并评价节约水电活动的效果.
25.(2021·山东济南市·九年级一模)加强劳动教育是学校贯彻“五育并举”的重要举措.为了解学生参加各项劳动的情况,某校对七年级部分学生进行了随机问卷调查,其中一个问题是“你每周在家参加家务劳动的时间是多少?”,共有如下四个选项:
A.1小时以下
B.1~2小时(不包含2小时)
C.2~3小时(包含2小时)
D.3小时以上
图①、图②是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
(1)填空:本次问卷调查一共调查了______名学生;(2)请将图①的条形统计图补充完整;
(3)并求出图②中D部分所对应的圆心角度数;(4)若该校共有1800名学生,请你估计全校可能有多少名学生每周在家参加家务劳动的时间在2小时以上(包含2小时)?
2020-2021学年浙教版七年级下册数学
单元测评培优卷(原版+解析版)
第10章
数据的收集、整理与描述
(测试时间:120分钟,满分:120分)
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2021·福建省福州第一中学七年级期中)下列调查中,调查方式选择合理的是(
)
A.为了了解某一批灯泡的寿命,选择全面调查
B.为了了解一批袋装食品是否含有防腐剂,选择全面调查
C.为了了解“天问一号”的设备零件的质量情况,选择抽样调查
D.为了了解某年福州市的空气质量,选择抽样调查
【答案】D
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
【详解】A.为了了解某一批灯泡的寿命,应选择抽样调查,不合题意;
B.为了了解一批袋装食品是否含有防腐剂,应选择抽样调查,不合题意;
C.为了了解“天问一号”的设备零件的质量情况,应该选择全面调查,不合题意;
D.为了了解某年福州市的空气质量,应该选择抽样调查,符合题意;故选:D.
【点睛】本题考查了抽样调查和全面调查,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
2.(2020春?高新区期中)今年某校有2000名学生参加线上学习,为了解这些学生的数学成绩,从中抽取100名考生的数学成绩进行统计分析,以下说法正确的是( )
A.2000名学生是总体
B.每位学生的数学成绩是个体
C.这100名学生是总体的一个样本
D.100名学生是样本容量
【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.
【解答】解:A、2000名学生的数学成绩是总体,故选项不合题意;
B、每位学生的数学成绩是个体,故选项符合题意;
C、这100名学生的数学成绩是总体的一个样本,故选项不合题意;
D、样本容量是100,故选项不合题意;故选:B.
【点睛】本题主要考查了总体、个体、样本和样本容量的定义,解题要分清具体问题中的总体、个体与样本的区别,关键是明确考查对象的范围.样本容量只是个数字,没有单位.
3.(2021·湖南常德市·七年级期末)为了准确反映某车队8名司机6月份耗去的汽油费用,且便于比较,那么选用最合适、直观的统计图是(
)
A.折线统计图
B.扇形统计图
C.条形统计图
D.统计表
【答案】C
【分析】根据题意的要求,结合统计图的特点作出判断即可.
【详解】解:根据题意,要求清楚地比较8名司机的汽油费用,
而条形统计图能清楚地表示出每个项目的具体数目,符合要求.故选:C.
【点睛】考查统计图的选择,解决此类问题,需要明确题意的要求,根据统计图的特点选择合适的统计图.
4.(2020秋?南关区校级期中)我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1500石,验得米内夹谷,抽样取米一把,数得250粒内夹谷30粒.则这批米内夹谷约为( )
A.140石
B.160石
C.180石
D.200石
【分析】根据总体平均数约等于样本平均数列出算式,再进行计算即可得出答案.
【解答】解:根据题意得:1500180(石),答:这批米内夹谷约为180石;故选:C.
【点睛】本题考查的是通过样本去估计总体,总体平均数约等于样本平均数.
5.(2020·北京)北京市实施垃圾分类以来,为了调动居民参与垃圾分类的积极性,某社区实行垃圾分类积分兑换奖品活动.随机抽取了若干户5月份的积分情况,并对抽取的样本进行了整理得到下列不完整的统计表:
积分x/分
频数
频率
0≤x<50
4
0.1
50≤x<100
8
0.2
100≤x<200
16
b
x≥200
a
0.3
根据以上信息可得( )
A.a=40,b=0.4
B.a=12,b=0.4
C.a=10,b=0.5
D.a=4,b=0.5
【答案】B
【分析】根据0≤x<50的频数和频率求出抽取的总数,再根据频数=总数×频率求出a,频率=频数÷总数求出b即可.
【详解】解:∵总数为:4÷0.1=40∴a=40×0.3=12,b=16÷40=0.4故选B.
【点睛】本题主要考查了数据分析,数据处理,熟练频数、频率和总数之间的关系是解决本题的关键.
6.(2020·北京市三帆中学初三期中)为加强锻炼增强体魄,我校初三(1)班同学组建了足球、篮球、乒乓球、跳绳四个体育活动小组.经调查,全班同学全员参与各活动小组人数分布情况的扇形图和条形图如图所示:①该班有50名学生;②篮球有16人;③跳绳人数所占扇形圆心角为57.6°;④足球人数所占扇形圆心角为120°。这四种说法中正确的有( )
A.2个
B.0个
C.1个
D.3个
【答案】C
【分析】①根据乒乓球的人数和所占的百分比求出总人数;②用总人数减去其它项目的人数,求出篮球的人数;③用360°乘以跳绳人数所占的百分比即可得出答案;④用360°乘以足球人数所占的百分比即可得出答案.
【解析】解:①该班学生数是:12÷=48(名),故本选项错误;
②篮球有:48﹣16﹣12﹣8=12(人),故本选项错误;
③跳绳人数所占扇形圆心角为360°×=60°,故本选项错误;
④足球人数所占扇形圆心角为360°×=120°,故本选项正确;这四种说法中正确的有1个,选:C.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
7.(2021·安徽九年级专题练习)某城市经济生产总值最近4年的增长情况如图所示,请判断下列说法中正确的为(
)
A.2013年到2016年该城市的经济生产总值不变
B.2013年到2016年该城市的经济生产总值一直在下降
C.2013年到2016年该城市的经济生产总值有升有降
D.2013年到2016年该城市的经济生产总值一直在上升
【答案】D
【分析】图中数据为生产总值增长率,而不是生产总值,根据折线统计图可知增长率均为正数,所以生产总值一直在增加,只是生产总值的增长率有升有降.
【详解】由图知,每年的增长率都是正数,说明从2013年到2016年,该城市的经济生产总值一直在增加,只是增长的幅度有快有慢而已.故选:D
【点睛】本题主要考查折线统计图的运用,折线统计图表示的是事物的变化情况.读懂统计图,从统计图中得到必要的信息是解决问题的关键.
8.(2020春?南岗区校级期中)一个容量为80的样本,最大值为50,最小值为9,取组距为10,则可以分成( )
A.4组
B.5组
C.9组
D.10组
【分析】最大值与最小值的差,除以组距即得组数.
【解答】解:(50﹣9)÷10=4.1,故分成5组较好.故选:B.
【点睛】本题考查频率分布直方图的制作方法,用最大值与最小值的差除以组距可得组数,不是整数用进一法取近似值确定组数.
9.(2020·北京九年级专题练习)某旅游城市为向游客介绍本地的气温情况,绘制了一年中12个月平均最高气温和平均最低气温的雷达图,图中点表示10月的平均最高气温约为,点表示4月的平均最低气温约为,下面叙述不正确的是(
)
A.各月的平均最低气温都在0以上
B.平均最高气温高于的月份有5个
C.3月和11月的最高气温基本相同
D.7月的平均温差比1月的平均温差大
【答案】B
【分析】根据平均最高气温和平均最低气温的雷达图进行推理判断即可.
【详解】解:.由雷达图知各月的平均最低气温都在0以上,正确,故这个选项不符合题意;
.平均最高气温高于的月份有7,8两个月,错误,故这个选项符合题意;
.3月和11月的平均最高气温基本相同,都为,正确,故这个选项不符合题意;
.7月的平均温差大约在左右,1月的平均温差在左右,故7月的平均温差比1月的平均温差大,正确,故这个选项不符合题意,故选:.
【点睛】本题主要考查象形统计图的应用,根据平均最高气温和平均最低气温的雷达图,利用图象法进行判断是解决本题的关键.
10.(2020·北京门头沟初一期末)近年来,某市旅游事业稳步发展,下面是根据该市旅游网提供的数据制成的
2016
年~2019年旅游总人数和旅游总收入同比增长率统计图:下面有三个推断:
①
从
2016
年到
2019
年,年旅游总人数增长最多的是
2018
年,比上一年增长了
0.3
亿人次;
②
从
2016
年到
2019
年,年旅游总收入最高的是
2018
年;
③
如果
2016
年旅游总收入为
2
442.1
亿元,那么
2015
年旅游总收入约为
2
220
亿元.
其中所有合理的推断的序号是(
)
A.①②
B.②③
C.①③
D.①②③
【答案】C
【分析】①由条形图,分别计算从2016年到2019年年旅游总人数增长量,再比较即可;
②由折线图可得:从2016年到2019年,年旅游总收入最高的是2019年;
③由2016年旅游总收入为2442.1亿元,增长率为10%,即可求得2015年旅游总收入.
【解析】解:①∵1.84-1.70=0.14,2.14-1.84=0.30,2.31-2.14=0.17,而0.14<0.17<0.30,
∴从2016年到2019年,年旅游总人数增长最多的是2018年,比上一年增长了0.3亿人次,故本选项推断合理;②由折线图可知,从2016年到2019年,旅游总收入同比增长率连年增加,所以年旅游总收入最高的是2019年,故本选项推断不合理;
③∵2016年旅游总收入为2442.1亿元,增长率为10%,∴2442.1÷(1+10%)≈2220(亿元),
∴2015年旅游总收入约为2220亿元,故本选项推断合理.综上所述:①③推断合理,故选:C.
【点睛】此题考查了条形统计图与折线统计图的知识.难度适中,注意掌握数形结合思想的应用.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020·四川达州中考真题)2019年是中华人民共和国成立70周年,天安门广场举行了盛大的国庆阅兵式和群众游行活动.其中,群众游行队伍以“同心共筑中国梦”为主题,包含有“建国创业”“改革开放”“伟大复兴”三个部分,某同学要统计本班学生最喜欢哪个部分,制作扇形统计图.以下是打乱了的统计步骤:①绘制扇形统计图;②收集三个部分本班学生喜欢的人数;③计算扇形统计图中三个部分所占的百分比。其中正确的统计顺序是____________.
【答案】②③①
【分析】制作扇形统计图的一般步骤是:1、计算各部分在总体中所占的百分比;2、计算各个扇形的圆心角的度数;3、在圆中依次作出上面的扇形,并标出百分比;据此解答即可.
【解析】解:正确的统计顺序是:②收集三个部分本班学生喜欢的人数;③计算扇形统计图中三个部分所占的百分比;①绘制扇形统计图;故答案为:②③①.
【点睛】本题考查了扇形统计图的相关知识,解题的关键明确制作扇形统计图的一般步骤.
12.(2020春?江阴市校级期中)老师在黑板上随手写下一串数字“010010001”,则数字“0”出现的频率是 .
【分析】利用频率的计算方法计算即可.
【解答】解:数字“0”出现的频率是:,故答案为:.
【点睛】此题主要考查了频数与频率,关键是掌握频率=频数除以总数.
13.(2020春?西城区校级期中)当前,“低头族”已成为热门话题之一,为了了解路边行人边走路边低头看手机的情况,应采用的收集数据的方式是
;
A.对学校的同学发放问卷进行调查B.对在路边行走的学生随机发放问卷进行调查
C.对在图书馆里看书的人发放问卷进行调查D.对在路边行走的路人随机发放问卷进行调查
并说出你的理由
.
【分析】根据抽取的样本要具有代表性解答.
【解答】解:为了了解路边行人边走路边低头看手机的情况,应采用的收集数据的方式是对在路边行走的路人随机发放问卷进行调查,理由是抽取的样本具有代表性,故答案为:D;样本具有代表性.
【点睛】本题考查的是抽样调查,掌握收集数据时,抽取的样本要具有代表性是解题的关键.
14.(2020秋?永安市期中)为了估计池塘里有多少条鱼,我们从池塘里捕上100条做上标记,然后放回池塘里,经过一段时间待带标记的鱼完全混合于鱼群中后,第二次捕得200条,发现其中带标记的鱼25条,通过这种调查方式,我们可以估计出这个池塘里有
条鱼.
【分析】200条鱼,发现带有记号的鱼有25条,则可求出带记号的鱼所占的百分比,再根据带记号的总计有100条,即可求得湖里鱼的总条数.
【解答】解:设这个池塘里鱼大约有x条,根据题意,得:,解得:x=800,
经检验:x=800是分式方程的解,所以估计这个池塘里有800条鱼,故答案为:800.
【点睛】此题考查了用样本估计总体的思想.总体中带记号的鱼所占的百分比约等于样本中带记号的鱼所占的百分比.
15.(2020春?句容市期中)将某班男生的身高分成了三组,情况如表所示,则表中b的值是 30% .
第一组
第二组
第三组
频数
6
10
a
频率
b
c
20%
【分析】根据各小组的频率之和等于1,即可得出第一组与第二组的频率和,然后求出数据总数,从而求出b的值.
【解答】解:∵第一组与第二组的频率之和为1﹣20%=80%,
∴该班男生的总人数为(6+10)÷80%=20,∴b=6÷20=30%.故答案为:30%.
【点睛】本题主要考查了频数与频率,频率是指每个对象出现的次数与总次数的比值(或者百分比),即频率=频数÷总数.
16.(2021·北京四中七年级期中)在1~7月份,某种水果的每斤进价与每斤售价的信息如图所示,则出售该种水果每斤利润最大的月份是_____月份.
【答案】4
【分析】根据图象中的信息即可得到结论.
【详解】由图象中的信息可知,1月份每斤的利润=10.8-10=0.8元,
2月份每斤的利润=9-7=2元,3月份每斤的利润=7.5﹣4.5=3元,
4月份每斤的利润=6﹣2.5=3.5元,5月份每斤的利润=4.5﹣2=2.5元,
6月份每斤的利润=3﹣1.8=1.2元,7月份每斤的利润=1.5﹣1.2=0.3元,
故出售该种水果每斤利润最大的月份是4月份,故答案为4
【点睛】本题考查了象形统计图,有理数大小的比较,正确的把握图象中的信息,理解利润=售价﹣进价是解题的关键.
17.(2021·北京九年级一模)在国家统计局发布的我国2020年国民经济和社会发展统计公报中,给出了统计图1和图2.
(1)估计2021年全年国内生产总值(GDP)是__________亿元;
(2)利用你所学知识观察、分析、比较图1和图2中数据,写出2016﹣2020年国内生产总值(GDP)和三次产业的占比的变化趋势是__________.
【答案】
2016﹣2020年国内生产总值(GDP)不断增加,但增长速度趋于稳定,三次产业的占比的变化趋势是下降趋势.
【分析】(1)由图1中的信息列式计算即可;(2)根据统计图中的信息即可得到结论.
【详解】解:(1),故答案为:;
(2)根据统计图中的信息得:2016﹣2020年国内生产总值(GDP)不断增加,但增长速度趋于稳定,三次产业的占比的变化趋势是下降趋势.
故答案为:2016﹣2020年国内生产总值(GDP)不断增加,但增长速度趋于稳定,三次产业的占比的变化趋势是下降趋势.
【点睛】本题考查条形统计图等知识,是重要考点,难度较易,掌握相关知识是解题关键.
18.(2020·北京西城初三二模)某调查机构对某地互联网行业从业情况进行调查统计,得到当地互联网行业从业人员年龄分布统计图和当地90后从事互联网行业岗位分布统计图:
互联网行业从业人员年龄分布统计图
90后从事互联网行业岗位分布图
对于以下四种说法,你认为正确的是_____
(写出全部正确说法的序号).
①在当地互联网行业从业人员中,90后人数占总人数的一半以上
②在当地互联网行业从业人员中,80前人数占总人数的13%
③在当地互联网行业中,从事技术岗位的90后人数超过总人数的20%
④在当地互联网行业中,从事设计岗位的90后人数比80前人数少
【答案】①③
【分析】观察、比较扇形统计图和条形统计图获取相关信息,然后再进行分析即可
【解析】解:①从扇形统计图中可发现互联网行业从业人员中90后占56%,占一半以上,即①正确;
②互联网行业中从事技术岗位的80前人数占总人数1-56%-41%=3%,故②错误;.
③B互联网行业中从事技术岗位的90后人数占总人数的0.56×0.41=0.2296
>0.2,故③正确;
④从事设计岗位的90后人数占总人数的0.56×0.08=0.0448>0.03故选④错误;
故答案为①③.
【点睛】本题主要考查对扇形统计图和条形统计图的观察分析能力,掌握条形统计图和扇形统计图的关联是解答本题的关键.
三、解答题(本大题共7小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020秋?增城区期末)根据电力部门统计,每天8:00至21:00是用电的高峰期,简称“峰时”,21:00至次日8:00是用电的低谷时期,简称“谷时”.为了缓解供电需求紧张的矛盾,某市电力部门于2020年10月统一换装“峰谷分时”电表,对用电实行“峰谷分时电价”新政策,具体见表:
时间
换表前
换表后
电价
每度0.52元
峰时(8:00~21:00)
谷时(21:00~次日8:00)
每度0.55元
每度0.30元
(1)若小王家9月份(换表前)的用电量为80度,则该月电费为
元;
(2)小张家11月份“峰时”用电50度,“谷时”用电20度,问小张家11月份的电费是多少元?
(3)小李家12月份用电95度,经测算比换表前使用95度电节省了5.9元,问小李家12月份使用“峰时电”和“谷时电”分别是多少度?
【分析】(1)用用电度数乘以换表前每度的价钱即可;(2)根据11月份电费=“峰时”用电量ד峰时”单价+“谷时”用电量ד谷时”单价列式计算即可;(3)可设小张家这个月使用“峰时”电是x度,则“谷时”电是(95﹣x)度,根据题意列出方程解答即可.
【解答】解:(1)小王家9月份(换表前)的用电量为80度,则该月电费为80×0.52=41.6(元),
故答案为:41.6;(2)小张家11月份的电费是50×0.55+20×0.30=33.5(元);
(3)设小李家12月使用“峰时”电是x度,则“谷时”电是(95﹣x)度,
根据题意得0.55x+0.30(95﹣x)=0.52×95﹣5.9,解得x=60,95﹣x=95﹣60=35.
答:小李家12月使用“峰时”用电60度,谷时用电35度.
【点睛】本题考查了统计表、一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
20.(2020秋?历城区期末)小强是校学生会体育部部长,他想了解现在同学们更喜欢什么球类运动,以便学生会组织比赛,小强随机调查了300名同学,调在结果如下表:
最喜欢的球类运动
篮球
足球
排球
乒乓球
羽毛球
其他
人数
68
m
27
90
36
9
(1)本次调查结果中喜欢足球运动项目的人数m= ;
(2)本次调查结果中喜欢排球运动项目的人数占调查总人数的百分比是 ;
(3)根据调查数据,在绘制扇形统计图的过程中,羽毛球所对应扇形的圆心角度数等于 °;
(4)如果你是体育部长,根据调查的结果,你会组织什么比赛?说说你的理由.
【分析】(1)根据题意和表格中的数据,可以计算出m的值;(2)根据表格中的数据,可以计算出本次调查结果中喜欢排球运动项目的人数占调查总人数的百分比;(3)根据表格中的数据可以计算出羽毛球所对应扇形的圆心角度数;(4)本题答案不唯一,只要合理即可.
【解答】解:(1)由表格可得,m=300﹣68﹣27﹣90﹣36﹣9=70,故答案为:70;
(2)本次调查结果中喜欢排球运动项目的人数占调查总人数的百分比是100%=9%,
故答案为:9%;
(3)羽毛球所对应扇形的圆心角度数为:360°108°,故答案为:108;
(4)组织乒乓球比赛、篮球比赛和足球比赛,理由:由表格可知,喜欢乒乓球、足球和篮球的学生比较多,故可以组织乒乓球比赛、篮球比赛和足球比赛.
【点睛】本题考查扇形统计图,解答本题的关键是明确题意,利用扇形统计图的知识解答.
21.(2021·河南南阳市·九年级一模)2020年国家提出并部署了“新基建”项目,主要包含“特高压,城际高速铁路和城市轨道交通,5G基站建设,工业互联网,大数据中心,人工智能,新能源汽车充电桩”等.《2020新基建中高端人才市场就业吸引力报告》重点刻画了“新基建”中五大细分领域(5G基站建设,工业互联网,大数据中心,人工智能,新能源汽车充电桩)总体的人才与就业机会.下图是其中的一个统计图.
请根据图中信息,解答下列问题:
(1)图中2020年“新基建”七大领域预计投资规模的平均数约是________亿元(结果保留一位小数);
(2)在由“新基建”七大领域预计投资规模组成的扇形统计图中,“新能源汽车充电桩”预计投资规模所占的圆心角约是_______(结果保留整数);(3)甲,乙两位待业人员,仅根据上面统计图中的数据,从五大细分领域中,甲选择了“5G基站建设”,乙选择了“人工智能”分别作为自己的就业方向,请简要说明他们选择就业方向的理由各是什么.
【答案】(1)314.6;(2)49;(3)甲更关注在线职位增长率;乙关注的是2020年预计投资规模最大
【分析】(1)按照求平均数的公式计算即可,即把七大领域预计投资规模数相加并除以7,就可得平均数;
(2)计算“新能源汽车充电桩”预计投资规模在七大领域预计投资规模总数中的百分数,它与360°的积就是所求扇形的圆心角;(3)观察统计图知,“5G基站建设”
在线职位增长率最大,故甲关注它;而“人工智能”则是五大细分领域中2020年预计投资规模最大的,故乙关注它.
【详解】(1)2020年“新基建”七大领域预计投资规模的平均数为:
(100+640+300+200+160+500+300)÷7≈314.3(亿元)故答案为:314.3
(2)故答案为:49
(3)五大细分领域中,“5G基站建设”
在线职位与2019年同期相比,增长率最大,所以甲关注的是这个增长率;而“人工智能”则是五大细分领域中2020年预计投资规模最大的,故乙关注它.
【点睛】本题综合考查了各种统计图,关键是读懂统计图,获取所需要的信息.
22.(2020·北京大兴初三一模)新冠肺炎疫情暴发后,一场同时间赛跑、与病魔较量的战役随即打响.在疫情防控一线,除了广大医务工作者义无反顾、日夜奋战之外,在另一条战线上,科研人员也在加班加点、紧急攻关.全国科技战线积极响应党中央号召,科技、卫健等12个部门组成科研攻关组,短短一个月的时间内就取得了积极进展.3月13日0﹣24时,31个省(自治区、直辖市)和新疆生产建设兵团新增确诊病例11例(数据不含港澳台),新增疑似病例17例(数据不含港澳台).如图是根据国家卫健委关于新型冠状病毒肺炎通报的数据(数据不含港澳台)绘制的统计图:
根据以上信息,回答下列问题:
(1)下列推断合理的是_______.
①2月15日武汉新增确诊病例约为1500例;②从2月23日起到3月13日止,武汉每日新增确诊病例都在500例以下;③从2月23日起到3月13日止,全国每日新增疑似病例逐渐减少.④3月13日湖北新增疑似病例不超过17例.
(2)结合本题的信息及当前防疫形势,说说你的感受.
【答案】(1)①④;(2)见解析.
【分析】(1)利用图中信息一一判断即可.(2)结合本题的信息及当前防疫形势,说说自己的感受即可.
【解析】(1)由图中信息可知:①2月15日武汉新增确诊病例约为1500例,正确.
②从2月23日起到3月13日止,武汉每日新增确诊病例都在500例以下,错误,2月24日前每日新增确诊病例都在500以上.③从2月23日起到3月13日止,全国每日新增疑似病例逐渐减少.错误,其中2月18日到2月20日是逐渐增加的.④3月13日湖北新增疑似病例不超过17例.正确.故答案为①④.
(2)国内疫情防控科学有效,防控形势持续向好.相信中国一定能打赢这场战疫.
【点睛】本题考查折线统计图,解题的关键是读懂图象信息,属于中考常考题型.
23.(2020·北京通州初三一模)国务院发布的《全民科学素质行动计划纲要实施方案(2016-2020年)》指出:公民科学素质是实施创新驱动发展战略的基础,是国家综合国力的体现.《方案》明确提出,2020年要将我国公民科学素质的数值提升到10%以上.为了解我国公民科学素质水平及发展状况,中国科协等单位已多次组织了全国范围的调查,以下是根据调查结果整理得到的部分信息.注:科学素质的数值是指具备一定科学素质的公民人数占公民总数的百分比.
.2015和2018年我国各直辖市公民科学素质发展状况统计图如下:
2015年
2018年
男
女
b.2015年和2018年我国公民科学素质发展状况按性别分类统计如下:
c.2001年以来我国公民科学素质水平发展统计图如下:
根据以上信息,回答下列问题:
(1)在我国四个直辖市中,从2015年到2018年,公民科学素质水平增幅最大的城市是________,公民科学素质水平增速最快的城市是_________.注:科学素质水平增幅=2018年科学素质的数值一2015年科学素质的数值;科学素质水平增速=(2018年科学素质的数值一2015年科学素质的数值)÷2015年科学素质的数值.
(2)已知在2015年的调查样本中,男女公民的比例约为1:1,则2015年我国公民的科学素质水平为______%(结果保留一位小数);由计算可知.在2018年的调查样本中.男性公民人数_____女性公民人数(填“多于”、“等于”或“少于”).(3)根据截至2018年的调查数据推断,你认为“2020年我国公民科学素质提升到10%以上”的目标能够实现吗?请说明理由.
【答案】(1)北京,重庆;(2)6.2,少于;(3)见解析
【分析】(1)利用条形统计图中信息判断即可.(2)利用表格和折线统计图信息,解决问题即可.
(3)答案不唯一,说法合理即可.
【解析】解:(1)由2015和2018年我国各直辖市公民科学素质发展状况统计图如图1得知,
上海:22%-19%=3%,北京:21.5%-17.5%=4%,天津:14%-12%=2%,重庆:8%-4.5%=3.5%,
故在我国四个直辖市中,从2015年到2018年,公民科学素质水平增幅最大的城市是北京;
上海:3%÷19%≈16%,北京:4%÷21.5%≈19%,天津:2%÷12%≈17%,重庆:3.5%÷4.5%=78%,
故公民科学素质水平增速最快的城市是重庆;故答案为:北京,重庆;
(2)∵在2015年的调查样本中,男女公民的比例约为1:1,
∴2015年我国公民的科学素质水平为(9.0%+3.4%)÷2=6.2%,
设男性公民占x%,则有11.1%×x%+6.2%×(1-x%)=8.5%,解得x=47,
∴男性公民人数少于女性公民人数,故答案为6.2,少于.
(3)①能实现.理由如下:
2015年我国公民的科学素质水平为6.2%,2018年我国公民的科学素质水平为8.5%,平均每年的增幅平均为0.77%,
如果按照匀速增长的速度推断,2020年我国公民的科学素质水平达到10.3%,
由此可知,“2020年我国公民科学素质提升到10%以上”的目标能够实现.
②条件不足,无法判断.理由如下:一种情形同①,能实现目标.另一种情形,无法判断.
因为不知道2018~2020年间我国公民的科学素质水平的增从速度是加快还是减缓,所以无法判断,2020年能否实现目标.
【点睛】本题考查条形统计图,统计表,折线统计图等知识,解题的关键是理解题意,读懂图象信息,属于中考常考题型.
24.(2019·浙江江干初二期末)为了节约能源,某城市开展了节约水电活动,已知该城市共有10000户家庭,活动前,某调查小组随机抽取了部分家庭每月的水电费的开支(单位:元),结果如左图所示频数直方图(每一组含前一个边界值,不含后一个边界值);活动后,再次调查这些家庭每月的水电费的开支,结果如表所示:
(1)求所抽取的样本的容量;(2)如以每月水电费开支在225元以下(不含)为达到节约标准,请问通过本次活动,该城市大约增加了多少户家庭达到节约标准?(3)活动后,这些样本家庭每月水电费开支的总额能否低于6000元?(4)请选择一个适当的统计量分析活动前后的相关数据,并评价节约水电活动的效果.
【答案】(1)40;(2)1250户;(3)活动后,这些样本家庭每月水电费开支的总额不低于6000元.(4)开支在225以下的户数上可以看出节约水电活动的效果还不错.
【分析】(1)将频数分布直方图各分组频数相加即可得样本容量;
(2)分别计算出活动前、后达到节约标准的家庭数,相减即可得;
(3)取各分组的组中值,再分别乘以各分组的频数,相加即可得;
(4)根据统计图中的数据可以解答本题,本题答案不唯一,只要合理即可..
【解析】解:(1)所抽取的样本的容量为6+12+11+7+3+1=40;
(2)活动前达到节约标准的家庭数为10000×=7250(户),
活动后达到节约标准的家庭数为10000×=8500(户),85007250=1250(户),
∴该城市大约增加了1250户家庭达到节约标准;
(3)这40户家庭每月水电费开支总额为:
7×100+13×150+14×200+4×250+2×300=7050(元),
∴活动后,这些样本家庭每月水电费开支的总额不低于6000元.
(4)根据题意可知,开支在225以下的户数上可以看出节约水电活动的效果还不错.
【点睛】本题考查的是频数分布直方图的运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.频数分布直方图能清楚地表示出每个项目的数据.
25.(2021·山东济南市·九年级一模)加强劳动教育是学校贯彻“五育并举”的重要举措.为了解学生参加各项劳动的情况,某校对七年级部分学生进行了随机问卷调查,其中一个问题是“你每周在家参加家务劳动的时间是多少?”,共有如下四个选项:
A.1小时以下
B.1~2小时(不包含2小时)
C.2~3小时(包含2小时)
D.3小时以上
图①、图②是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
(1)填空:本次问卷调查一共调查了______名学生;(2)请将图①的条形统计图补充完整;
(3)并求出图②中D部分所对应的圆心角度数;(4)若该校共有1800名学生,请你估计全校可能有多少名学生每周在家参加家务劳动的时间在2小时以上(包含2小时)?
【答案】(1)200;(2)见解析;(3);(4)估计全校可能有360名学生每周在家参加家务劳动的时间在2小时以上(包含2小时)
【分析】(1)根据B选项人数及其占被调查人数的比例计算即可得出答案.(2)用总人数减去其他选项的人数求出D选项的人数,即可补全统计图;(3)用乘以D部分所占的百分比即可得出D部分所对应的圆心角度数;(4)用该校的总人数乘以每周在家参加家务劳动的时间在2小时以上(包含2小时)的人数所占的百分比即可.
【详解】解:(1)本次问卷调查一共调查的学生数是:(名)故答案为:200;
(2)劳动的时间在3小时以上的人数有:(名),补全统计图如下:
(3)D部分所对应的圆心角度数是;
(4)根据题意得:(名),
答:估计全校可能有360名学生每周在家参加家务劳动的时间在2小时以上(包含2小时).
【点睛】本题考查条形统计图、扇形统计图等知识,解题的关键是熟练掌握基本概念,学会用样本估计总体的思想解决问题,属于基础题,中考常考题型.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2020-2021学年浙教版七年级下册数学
单元测评培优卷(原版+解析版)
第10章
数据的收集、整理与描述
(测试时间:120分钟,满分:120分)
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2021·福建省福州第一中学七年级期中)下列调查中,调查方式选择合理的是(
)
A.为了了解某一批灯泡的寿命,选择全面调查
B.为了了解一批袋装食品是否含有防腐剂,选择全面调查
C.为了了解“天问一号”的设备零件的质量情况,选择抽样调查
D.为了了解某年福州市的空气质量,选择抽样调查
2.(2020春?高新区期中)今年某校有2000名学生参加线上学习,为了解这些学生的数学成绩,从中抽取100名考生的数学成绩进行统计分析,以下说法正确的是( )
A.2000名学生是总体
B.每位学生的数学成绩是个体
C.这100名学生是总体的一个样本
D.100名学生是样本容量
3.(2021·湖南常德市·七年级期末)为了准确反映某车队8名司机6月份耗去的汽油费用,且便于比较,那么选用最合适、直观的统计图是(
)
A.折线统计图
B.扇形统计图
C.条形统计图
D.统计表
4.(2020秋?南关区校级期中)我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1500石,验得米内夹谷,抽样取米一把,数得250粒内夹谷30粒.则这批米内夹谷约为( )
A.140石
B.160石
C.180石
D.200石
5.(2020·北京)北京市实施垃圾分类以来,为了调动居民参与垃圾分类的积极性,某社区实行垃圾分类积分兑换奖品活动.随机抽取了若干户5月份的积分情况,并对抽取的样本进行了整理得到下列不完整的统计表:
积分x/分
频数
频率
0≤x<50
4
0.1
50≤x<100
8
0.2
100≤x<200
16
b
x≥200
a
0.3
根据以上信息可得( )
A.a=40,b=0.4
B.a=12,b=0.4
C.a=10,b=0.5
D.a=4,b=0.5
6.(2020·北京市三帆中学初三期中)为加强锻炼增强体魄,我校初三(1)班同学组建了足球、篮球、乒乓球、跳绳四个体育活动小组.经调查,全班同学全员参与各活动小组人数分布情况的扇形图和条形图如图所示:①该班有50名学生;②篮球有16人;③跳绳人数所占扇形圆心角为57.6°;④足球人数所占扇形圆心角为120°。这四种说法中正确的有( )
A.2个
B.0个
C.1个
D.3个
7.(2021·安徽九年级专题练习)某城市经济生产总值最近4年的增长情况如图所示,请判断下列说法中正确的为(
)
A.2013年到2016年该城市的经济生产总值不变
B.2013年到2016年该城市的经济生产总值一直在下降
C.2013年到2016年该城市的经济生产总值有升有降
D.2013年到2016年该城市的经济生产总值一直在上升
8.(2020春?南岗区校级期中)一个容量为80的样本,最大值为50,最小值为9,取组距为10,则可以分成( )
A.4组
B.5组
C.9组
D.10组
9.(2020·北京九年级专题练习)某旅游城市为向游客介绍本地的气温情况,绘制了一年中12个月平均最高气温和平均最低气温的雷达图,图中点表示10月的平均最高气温约为,点表示4月的平均最低气温约为,下面叙述不正确的是(
)
A.各月的平均最低气温都在0以上
B.平均最高气温高于的月份有5个
C.3月和11月的最高气温基本相同
D.7月的平均温差比1月的平均温差大
10.(2020·北京门头沟初一期末)近年来,某市旅游事业稳步发展,下面是根据该市旅游网提供的数据制成的
2016
年~2019年旅游总人数和旅游总收入同比增长率统计图:下面有三个推断:
①
从
2016
年到
2019
年,年旅游总人数增长最多的是
2018
年,比上一年增长了
0.3
亿人次;
②
从
2016
年到
2019
年,年旅游总收入最高的是
2018
年;
③
如果
2016
年旅游总收入为
2
442.1
亿元,那么
2015
年旅游总收入约为
2
220
亿元.
其中所有合理的推断的序号是(
)
A.①②
B.②③
C.①③
D.①②③
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020·四川达州中考真题)2019年是中华人民共和国成立70周年,天安门广场举行了盛大的国庆阅兵式和群众游行活动.其中,群众游行队伍以“同心共筑中国梦”为主题,包含有“建国创业”“改革开放”“伟大复兴”三个部分,某同学要统计本班学生最喜欢哪个部分,制作扇形统计图.以下是打乱了的统计步骤:①绘制扇形统计图;②收集三个部分本班学生喜欢的人数;③计算扇形统计图中三个部分所占的百分比。其中正确的统计顺序是____________.
12.(2020春?江阴市校级期中)老师在黑板上随手写下一串数字“010010001”,则数字“0”出现的频率是 .
13.(2020春?西城区校级期中)当前,“低头族”已成为热门话题之一,为了了解路边行人边走路边低头看手机的情况,应采用的收集数据的方式是
;
A.对学校的同学发放问卷进行调查B.对在路边行走的学生随机发放问卷进行调查
C.对在图书馆里看书的人发放问卷进行调查D.对在路边行走的路人随机发放问卷进行调查
并说出你的理由
.
14.(2020秋?永安市期中)为了估计池塘里有多少条鱼,我们从池塘里捕上100条做上标记,然后放回池塘里,经过一段时间待带标记的鱼完全混合于鱼群中后,第二次捕得200条,发现其中带标记的鱼25条,通过这种调查方式,我们可以估计出这个池塘里有
条鱼.
15.(2020春?句容市期中)将某班男生的身高分成了三组,情况如表所示,则表中b的值是 30% .
第一组
第二组
第三组
频数
6
10
a
频率
b
c
20%
16.(2021·北京四中七年级期中)在1~7月份,某种水果的每斤进价与每斤售价的信息如图所示,则出售该种水果每斤利润最大的月份是_____月份.
17.(2021·北京九年级一模)在国家统计局发布的我国2020年国民经济和社会发展统计公报中,给出了统计图1和图2.
(1)估计2021年全年国内生产总值(GDP)是__________亿元;
(2)利用你所学知识观察、分析、比较图1和图2中数据,写出2016﹣2020年国内生产总值(GDP)和三次产业的占比的变化趋势是__________.
18.(2020·北京西城初三二模)某调查机构对某地互联网行业从业情况进行调查统计,得到当地互联网行业从业人员年龄分布统计图和当地90后从事互联网行业岗位分布统计图:
互联网行业从业人员年龄分布统计图
90后从事互联网行业岗位分布图
对于以下四种说法,你认为正确的是_____
(写出全部正确说法的序号).
①在当地互联网行业从业人员中,90后人数占总人数的一半以上
②在当地互联网行业从业人员中,80前人数占总人数的13%
③在当地互联网行业中,从事技术岗位的90后人数超过总人数的20%
④在当地互联网行业中,从事设计岗位的90后人数比80前人数少
三、解答题(本大题共7小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020秋?增城区期末)根据电力部门统计,每天8:00至21:00是用电的高峰期,简称“峰时”,21:00至次日8:00是用电的低谷时期,简称“谷时”.为了缓解供电需求紧张的矛盾,某市电力部门于2020年10月统一换装“峰谷分时”电表,对用电实行“峰谷分时电价”新政策,具体见表:
时间
换表前
换表后
电价
每度0.52元
峰时(8:00~21:00)
谷时(21:00~次日8:00)
每度0.55元
每度0.30元
(1)若小王家9月份(换表前)的用电量为80度,则该月电费为
元;
(2)小张家11月份“峰时”用电50度,“谷时”用电20度,问小张家11月份的电费是多少元?
(3)小李家12月份用电95度,经测算比换表前使用95度电节省了5.9元,问小李家12月份使用“峰时电”和“谷时电”分别是多少度?
20.(2020秋?历城区期末)小强是校学生会体育部部长,他想了解现在同学们更喜欢什么球类运动,以便学生会组织比赛,小强随机调查了300名同学,调在结果如下表:
最喜欢的球类运动
篮球
足球
排球
乒乓球
羽毛球
其他
人数
68
m
27
90
36
9
(1)本次调查结果中喜欢足球运动项目的人数m= ;
(2)本次调查结果中喜欢排球运动项目的人数占调查总人数的百分比是 ;
(3)根据调查数据,在绘制扇形统计图的过程中,羽毛球所对应扇形的圆心角度数等于 °;
(4)如果你是体育部长,根据调查的结果,你会组织什么比赛?说说你的理由.
21.(2021·河南南阳市·九年级一模)2020年国家提出并部署了“新基建”项目,主要包含“特高压,城际高速铁路和城市轨道交通,5G基站建设,工业互联网,大数据中心,人工智能,新能源汽车充电桩”等.《2020新基建中高端人才市场就业吸引力报告》重点刻画了“新基建”中五大细分领域(5G基站建设,工业互联网,大数据中心,人工智能,新能源汽车充电桩)总体的人才与就业机会.下图是其中的一个统计图.
请根据图中信息,解答下列问题:
(1)图中2020年“新基建”七大领域预计投资规模的平均数约是________亿元(结果保留一位小数);
(2)在由“新基建”七大领域预计投资规模组成的扇形统计图中,“新能源汽车充电桩”预计投资规模所占的圆心角约是_______(结果保留整数);(3)甲,乙两位待业人员,仅根据上面统计图中的数据,从五大细分领域中,甲选择了“5G基站建设”,乙选择了“人工智能”分别作为自己的就业方向,请简要说明他们选择就业方向的理由各是什么.
22.(2020·北京大兴初三一模)新冠肺炎疫情暴发后,一场同时间赛跑、与病魔较量的战役随即打响.在疫情防控一线,除了广大医务工作者义无反顾、日夜奋战之外,在另一条战线上,科研人员也在加班加点、紧急攻关.全国科技战线积极响应党中央号召,科技、卫健等12个部门组成科研攻关组,短短一个月的时间内就取得了积极进展.3月13日0﹣24时,31个省(自治区、直辖市)和新疆生产建设兵团新增确诊病例11例(数据不含港澳台),新增疑似病例17例(数据不含港澳台).如图是根据国家卫健委关于新型冠状病毒肺炎通报的数据(数据不含港澳台)绘制的统计图:
根据以上信息,回答下列问题:
(1)下列推断合理的是_______.
①2月15日武汉新增确诊病例约为1500例;②从2月23日起到3月13日止,武汉每日新增确诊病例都在500例以下;③从2月23日起到3月13日止,全国每日新增疑似病例逐渐减少.④3月13日湖北新增疑似病例不超过17例.
(2)结合本题的信息及当前防疫形势,说说你的感受.
23.(2020·北京通州初三一模)国务院发布的《全民科学素质行动计划纲要实施方案(2016-2020年)》指出:公民科学素质是实施创新驱动发展战略的基础,是国家综合国力的体现.《方案》明确提出,2020年要将我国公民科学素质的数值提升到10%以上.为了解我国公民科学素质水平及发展状况,中国科协等单位已多次组织了全国范围的调查,以下是根据调查结果整理得到的部分信息.注:科学素质的数值是指具备一定科学素质的公民人数占公民总数的百分比.
.2015和2018年我国各直辖市公民科学素质发展状况统计图如下:
2015年
2018年
男
女
b.2015年和2018年我国公民科学素质发展状况按性别分类统计如下:
c.2001年以来我国公民科学素质水平发展统计图如下:
根据以上信息,回答下列问题:
(1)在我国四个直辖市中,从2015年到2018年,公民科学素质水平增幅最大的城市是________,公民科学素质水平增速最快的城市是_________.注:科学素质水平增幅=2018年科学素质的数值一2015年科学素质的数值;科学素质水平增速=(2018年科学素质的数值一2015年科学素质的数值)÷2015年科学素质的数值.
(2)已知在2015年的调查样本中,男女公民的比例约为1:1,则2015年我国公民的科学素质水平为______%(结果保留一位小数);由计算可知.在2018年的调查样本中.男性公民人数_____女性公民人数(填“多于”、“等于”或“少于”).(3)根据截至2018年的调查数据推断,你认为“2020年我国公民科学素质提升到10%以上”的目标能够实现吗?请说明理由.
24.(2019·浙江江干初二期末)为了节约能源,某城市开展了节约水电活动,已知该城市共有10000户家庭,活动前,某调查小组随机抽取了部分家庭每月的水电费的开支(单位:元),结果如左图所示频数直方图(每一组含前一个边界值,不含后一个边界值);活动后,再次调查这些家庭每月的水电费的开支,结果如表所示:
(1)求所抽取的样本的容量;(2)如以每月水电费开支在225元以下(不含)为达到节约标准,请问通过本次活动,该城市大约增加了多少户家庭达到节约标准?(3)活动后,这些样本家庭每月水电费开支的总额能否低于6000元?(4)请选择一个适当的统计量分析活动前后的相关数据,并评价节约水电活动的效果.
25.(2021·山东济南市·九年级一模)加强劳动教育是学校贯彻“五育并举”的重要举措.为了解学生参加各项劳动的情况,某校对七年级部分学生进行了随机问卷调查,其中一个问题是“你每周在家参加家务劳动的时间是多少?”,共有如下四个选项:
A.1小时以下
B.1~2小时(不包含2小时)
C.2~3小时(包含2小时)
D.3小时以上
图①、图②是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
(1)填空:本次问卷调查一共调查了______名学生;(2)请将图①的条形统计图补充完整;
(3)并求出图②中D部分所对应的圆心角度数;(4)若该校共有1800名学生,请你估计全校可能有多少名学生每周在家参加家务劳动的时间在2小时以上(包含2小时)?
2020-2021学年浙教版七年级下册数学
单元测评培优卷(原版+解析版)
第10章
数据的收集、整理与描述
(测试时间:120分钟,满分:120分)
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2021·福建省福州第一中学七年级期中)下列调查中,调查方式选择合理的是(
)
A.为了了解某一批灯泡的寿命,选择全面调查
B.为了了解一批袋装食品是否含有防腐剂,选择全面调查
C.为了了解“天问一号”的设备零件的质量情况,选择抽样调查
D.为了了解某年福州市的空气质量,选择抽样调查
【答案】D
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
【详解】A.为了了解某一批灯泡的寿命,应选择抽样调查,不合题意;
B.为了了解一批袋装食品是否含有防腐剂,应选择抽样调查,不合题意;
C.为了了解“天问一号”的设备零件的质量情况,应该选择全面调查,不合题意;
D.为了了解某年福州市的空气质量,应该选择抽样调查,符合题意;故选:D.
【点睛】本题考查了抽样调查和全面调查,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
2.(2020春?高新区期中)今年某校有2000名学生参加线上学习,为了解这些学生的数学成绩,从中抽取100名考生的数学成绩进行统计分析,以下说法正确的是( )
A.2000名学生是总体
B.每位学生的数学成绩是个体
C.这100名学生是总体的一个样本
D.100名学生是样本容量
【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.
【解答】解:A、2000名学生的数学成绩是总体,故选项不合题意;
B、每位学生的数学成绩是个体,故选项符合题意;
C、这100名学生的数学成绩是总体的一个样本,故选项不合题意;
D、样本容量是100,故选项不合题意;故选:B.
【点睛】本题主要考查了总体、个体、样本和样本容量的定义,解题要分清具体问题中的总体、个体与样本的区别,关键是明确考查对象的范围.样本容量只是个数字,没有单位.
3.(2021·湖南常德市·七年级期末)为了准确反映某车队8名司机6月份耗去的汽油费用,且便于比较,那么选用最合适、直观的统计图是(
)
A.折线统计图
B.扇形统计图
C.条形统计图
D.统计表
【答案】C
【分析】根据题意的要求,结合统计图的特点作出判断即可.
【详解】解:根据题意,要求清楚地比较8名司机的汽油费用,
而条形统计图能清楚地表示出每个项目的具体数目,符合要求.故选:C.
【点睛】考查统计图的选择,解决此类问题,需要明确题意的要求,根据统计图的特点选择合适的统计图.
4.(2020秋?南关区校级期中)我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1500石,验得米内夹谷,抽样取米一把,数得250粒内夹谷30粒.则这批米内夹谷约为( )
A.140石
B.160石
C.180石
D.200石
【分析】根据总体平均数约等于样本平均数列出算式,再进行计算即可得出答案.
【解答】解:根据题意得:1500180(石),答:这批米内夹谷约为180石;故选:C.
【点睛】本题考查的是通过样本去估计总体,总体平均数约等于样本平均数.
5.(2020·北京)北京市实施垃圾分类以来,为了调动居民参与垃圾分类的积极性,某社区实行垃圾分类积分兑换奖品活动.随机抽取了若干户5月份的积分情况,并对抽取的样本进行了整理得到下列不完整的统计表:
积分x/分
频数
频率
0≤x<50
4
0.1
50≤x<100
8
0.2
100≤x<200
16
b
x≥200
a
0.3
根据以上信息可得( )
A.a=40,b=0.4
B.a=12,b=0.4
C.a=10,b=0.5
D.a=4,b=0.5
【答案】B
【分析】根据0≤x<50的频数和频率求出抽取的总数,再根据频数=总数×频率求出a,频率=频数÷总数求出b即可.
【详解】解:∵总数为:4÷0.1=40∴a=40×0.3=12,b=16÷40=0.4故选B.
【点睛】本题主要考查了数据分析,数据处理,熟练频数、频率和总数之间的关系是解决本题的关键.
6.(2020·北京市三帆中学初三期中)为加强锻炼增强体魄,我校初三(1)班同学组建了足球、篮球、乒乓球、跳绳四个体育活动小组.经调查,全班同学全员参与各活动小组人数分布情况的扇形图和条形图如图所示:①该班有50名学生;②篮球有16人;③跳绳人数所占扇形圆心角为57.6°;④足球人数所占扇形圆心角为120°。这四种说法中正确的有( )
A.2个
B.0个
C.1个
D.3个
【答案】C
【分析】①根据乒乓球的人数和所占的百分比求出总人数;②用总人数减去其它项目的人数,求出篮球的人数;③用360°乘以跳绳人数所占的百分比即可得出答案;④用360°乘以足球人数所占的百分比即可得出答案.
【解析】解:①该班学生数是:12÷=48(名),故本选项错误;
②篮球有:48﹣16﹣12﹣8=12(人),故本选项错误;
③跳绳人数所占扇形圆心角为360°×=60°,故本选项错误;
④足球人数所占扇形圆心角为360°×=120°,故本选项正确;这四种说法中正确的有1个,选:C.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
7.(2021·安徽九年级专题练习)某城市经济生产总值最近4年的增长情况如图所示,请判断下列说法中正确的为(
)
A.2013年到2016年该城市的经济生产总值不变
B.2013年到2016年该城市的经济生产总值一直在下降
C.2013年到2016年该城市的经济生产总值有升有降
D.2013年到2016年该城市的经济生产总值一直在上升
【答案】D
【分析】图中数据为生产总值增长率,而不是生产总值,根据折线统计图可知增长率均为正数,所以生产总值一直在增加,只是生产总值的增长率有升有降.
【详解】由图知,每年的增长率都是正数,说明从2013年到2016年,该城市的经济生产总值一直在增加,只是增长的幅度有快有慢而已.故选:D
【点睛】本题主要考查折线统计图的运用,折线统计图表示的是事物的变化情况.读懂统计图,从统计图中得到必要的信息是解决问题的关键.
8.(2020春?南岗区校级期中)一个容量为80的样本,最大值为50,最小值为9,取组距为10,则可以分成( )
A.4组
B.5组
C.9组
D.10组
【分析】最大值与最小值的差,除以组距即得组数.
【解答】解:(50﹣9)÷10=4.1,故分成5组较好.故选:B.
【点睛】本题考查频率分布直方图的制作方法,用最大值与最小值的差除以组距可得组数,不是整数用进一法取近似值确定组数.
9.(2020·北京九年级专题练习)某旅游城市为向游客介绍本地的气温情况,绘制了一年中12个月平均最高气温和平均最低气温的雷达图,图中点表示10月的平均最高气温约为,点表示4月的平均最低气温约为,下面叙述不正确的是(
)
A.各月的平均最低气温都在0以上
B.平均最高气温高于的月份有5个
C.3月和11月的最高气温基本相同
D.7月的平均温差比1月的平均温差大
【答案】B
【分析】根据平均最高气温和平均最低气温的雷达图进行推理判断即可.
【详解】解:.由雷达图知各月的平均最低气温都在0以上,正确,故这个选项不符合题意;
.平均最高气温高于的月份有7,8两个月,错误,故这个选项符合题意;
.3月和11月的平均最高气温基本相同,都为,正确,故这个选项不符合题意;
.7月的平均温差大约在左右,1月的平均温差在左右,故7月的平均温差比1月的平均温差大,正确,故这个选项不符合题意,故选:.
【点睛】本题主要考查象形统计图的应用,根据平均最高气温和平均最低气温的雷达图,利用图象法进行判断是解决本题的关键.
10.(2020·北京门头沟初一期末)近年来,某市旅游事业稳步发展,下面是根据该市旅游网提供的数据制成的
2016
年~2019年旅游总人数和旅游总收入同比增长率统计图:下面有三个推断:
①
从
2016
年到
2019
年,年旅游总人数增长最多的是
2018
年,比上一年增长了
0.3
亿人次;
②
从
2016
年到
2019
年,年旅游总收入最高的是
2018
年;
③
如果
2016
年旅游总收入为
2
442.1
亿元,那么
2015
年旅游总收入约为
2
220
亿元.
其中所有合理的推断的序号是(
)
A.①②
B.②③
C.①③
D.①②③
【答案】C
【分析】①由条形图,分别计算从2016年到2019年年旅游总人数增长量,再比较即可;
②由折线图可得:从2016年到2019年,年旅游总收入最高的是2019年;
③由2016年旅游总收入为2442.1亿元,增长率为10%,即可求得2015年旅游总收入.
【解析】解:①∵1.84-1.70=0.14,2.14-1.84=0.30,2.31-2.14=0.17,而0.14<0.17<0.30,
∴从2016年到2019年,年旅游总人数增长最多的是2018年,比上一年增长了0.3亿人次,故本选项推断合理;②由折线图可知,从2016年到2019年,旅游总收入同比增长率连年增加,所以年旅游总收入最高的是2019年,故本选项推断不合理;
③∵2016年旅游总收入为2442.1亿元,增长率为10%,∴2442.1÷(1+10%)≈2220(亿元),
∴2015年旅游总收入约为2220亿元,故本选项推断合理.综上所述:①③推断合理,故选:C.
【点睛】此题考查了条形统计图与折线统计图的知识.难度适中,注意掌握数形结合思想的应用.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020·四川达州中考真题)2019年是中华人民共和国成立70周年,天安门广场举行了盛大的国庆阅兵式和群众游行活动.其中,群众游行队伍以“同心共筑中国梦”为主题,包含有“建国创业”“改革开放”“伟大复兴”三个部分,某同学要统计本班学生最喜欢哪个部分,制作扇形统计图.以下是打乱了的统计步骤:①绘制扇形统计图;②收集三个部分本班学生喜欢的人数;③计算扇形统计图中三个部分所占的百分比。其中正确的统计顺序是____________.
【答案】②③①
【分析】制作扇形统计图的一般步骤是:1、计算各部分在总体中所占的百分比;2、计算各个扇形的圆心角的度数;3、在圆中依次作出上面的扇形,并标出百分比;据此解答即可.
【解析】解:正确的统计顺序是:②收集三个部分本班学生喜欢的人数;③计算扇形统计图中三个部分所占的百分比;①绘制扇形统计图;故答案为:②③①.
【点睛】本题考查了扇形统计图的相关知识,解题的关键明确制作扇形统计图的一般步骤.
12.(2020春?江阴市校级期中)老师在黑板上随手写下一串数字“010010001”,则数字“0”出现的频率是 .
【分析】利用频率的计算方法计算即可.
【解答】解:数字“0”出现的频率是:,故答案为:.
【点睛】此题主要考查了频数与频率,关键是掌握频率=频数除以总数.
13.(2020春?西城区校级期中)当前,“低头族”已成为热门话题之一,为了了解路边行人边走路边低头看手机的情况,应采用的收集数据的方式是
;
A.对学校的同学发放问卷进行调查B.对在路边行走的学生随机发放问卷进行调查
C.对在图书馆里看书的人发放问卷进行调查D.对在路边行走的路人随机发放问卷进行调查
并说出你的理由
.
【分析】根据抽取的样本要具有代表性解答.
【解答】解:为了了解路边行人边走路边低头看手机的情况,应采用的收集数据的方式是对在路边行走的路人随机发放问卷进行调查,理由是抽取的样本具有代表性,故答案为:D;样本具有代表性.
【点睛】本题考查的是抽样调查,掌握收集数据时,抽取的样本要具有代表性是解题的关键.
14.(2020秋?永安市期中)为了估计池塘里有多少条鱼,我们从池塘里捕上100条做上标记,然后放回池塘里,经过一段时间待带标记的鱼完全混合于鱼群中后,第二次捕得200条,发现其中带标记的鱼25条,通过这种调查方式,我们可以估计出这个池塘里有
条鱼.
【分析】200条鱼,发现带有记号的鱼有25条,则可求出带记号的鱼所占的百分比,再根据带记号的总计有100条,即可求得湖里鱼的总条数.
【解答】解:设这个池塘里鱼大约有x条,根据题意,得:,解得:x=800,
经检验:x=800是分式方程的解,所以估计这个池塘里有800条鱼,故答案为:800.
【点睛】此题考查了用样本估计总体的思想.总体中带记号的鱼所占的百分比约等于样本中带记号的鱼所占的百分比.
15.(2020春?句容市期中)将某班男生的身高分成了三组,情况如表所示,则表中b的值是 30% .
第一组
第二组
第三组
频数
6
10
a
频率
b
c
20%
【分析】根据各小组的频率之和等于1,即可得出第一组与第二组的频率和,然后求出数据总数,从而求出b的值.
【解答】解:∵第一组与第二组的频率之和为1﹣20%=80%,
∴该班男生的总人数为(6+10)÷80%=20,∴b=6÷20=30%.故答案为:30%.
【点睛】本题主要考查了频数与频率,频率是指每个对象出现的次数与总次数的比值(或者百分比),即频率=频数÷总数.
16.(2021·北京四中七年级期中)在1~7月份,某种水果的每斤进价与每斤售价的信息如图所示,则出售该种水果每斤利润最大的月份是_____月份.
【答案】4
【分析】根据图象中的信息即可得到结论.
【详解】由图象中的信息可知,1月份每斤的利润=10.8-10=0.8元,
2月份每斤的利润=9-7=2元,3月份每斤的利润=7.5﹣4.5=3元,
4月份每斤的利润=6﹣2.5=3.5元,5月份每斤的利润=4.5﹣2=2.5元,
6月份每斤的利润=3﹣1.8=1.2元,7月份每斤的利润=1.5﹣1.2=0.3元,
故出售该种水果每斤利润最大的月份是4月份,故答案为4
【点睛】本题考查了象形统计图,有理数大小的比较,正确的把握图象中的信息,理解利润=售价﹣进价是解题的关键.
17.(2021·北京九年级一模)在国家统计局发布的我国2020年国民经济和社会发展统计公报中,给出了统计图1和图2.
(1)估计2021年全年国内生产总值(GDP)是__________亿元;
(2)利用你所学知识观察、分析、比较图1和图2中数据,写出2016﹣2020年国内生产总值(GDP)和三次产业的占比的变化趋势是__________.
【答案】
2016﹣2020年国内生产总值(GDP)不断增加,但增长速度趋于稳定,三次产业的占比的变化趋势是下降趋势.
【分析】(1)由图1中的信息列式计算即可;(2)根据统计图中的信息即可得到结论.
【详解】解:(1),故答案为:;
(2)根据统计图中的信息得:2016﹣2020年国内生产总值(GDP)不断增加,但增长速度趋于稳定,三次产业的占比的变化趋势是下降趋势.
故答案为:2016﹣2020年国内生产总值(GDP)不断增加,但增长速度趋于稳定,三次产业的占比的变化趋势是下降趋势.
【点睛】本题考查条形统计图等知识,是重要考点,难度较易,掌握相关知识是解题关键.
18.(2020·北京西城初三二模)某调查机构对某地互联网行业从业情况进行调查统计,得到当地互联网行业从业人员年龄分布统计图和当地90后从事互联网行业岗位分布统计图:
互联网行业从业人员年龄分布统计图
90后从事互联网行业岗位分布图
对于以下四种说法,你认为正确的是_____
(写出全部正确说法的序号).
①在当地互联网行业从业人员中,90后人数占总人数的一半以上
②在当地互联网行业从业人员中,80前人数占总人数的13%
③在当地互联网行业中,从事技术岗位的90后人数超过总人数的20%
④在当地互联网行业中,从事设计岗位的90后人数比80前人数少
【答案】①③
【分析】观察、比较扇形统计图和条形统计图获取相关信息,然后再进行分析即可
【解析】解:①从扇形统计图中可发现互联网行业从业人员中90后占56%,占一半以上,即①正确;
②互联网行业中从事技术岗位的80前人数占总人数1-56%-41%=3%,故②错误;.
③B互联网行业中从事技术岗位的90后人数占总人数的0.56×0.41=0.2296
>0.2,故③正确;
④从事设计岗位的90后人数占总人数的0.56×0.08=0.0448>0.03故选④错误;
故答案为①③.
【点睛】本题主要考查对扇形统计图和条形统计图的观察分析能力,掌握条形统计图和扇形统计图的关联是解答本题的关键.
三、解答题(本大题共7小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020秋?增城区期末)根据电力部门统计,每天8:00至21:00是用电的高峰期,简称“峰时”,21:00至次日8:00是用电的低谷时期,简称“谷时”.为了缓解供电需求紧张的矛盾,某市电力部门于2020年10月统一换装“峰谷分时”电表,对用电实行“峰谷分时电价”新政策,具体见表:
时间
换表前
换表后
电价
每度0.52元
峰时(8:00~21:00)
谷时(21:00~次日8:00)
每度0.55元
每度0.30元
(1)若小王家9月份(换表前)的用电量为80度,则该月电费为
元;
(2)小张家11月份“峰时”用电50度,“谷时”用电20度,问小张家11月份的电费是多少元?
(3)小李家12月份用电95度,经测算比换表前使用95度电节省了5.9元,问小李家12月份使用“峰时电”和“谷时电”分别是多少度?
【分析】(1)用用电度数乘以换表前每度的价钱即可;(2)根据11月份电费=“峰时”用电量ד峰时”单价+“谷时”用电量ד谷时”单价列式计算即可;(3)可设小张家这个月使用“峰时”电是x度,则“谷时”电是(95﹣x)度,根据题意列出方程解答即可.
【解答】解:(1)小王家9月份(换表前)的用电量为80度,则该月电费为80×0.52=41.6(元),
故答案为:41.6;(2)小张家11月份的电费是50×0.55+20×0.30=33.5(元);
(3)设小李家12月使用“峰时”电是x度,则“谷时”电是(95﹣x)度,
根据题意得0.55x+0.30(95﹣x)=0.52×95﹣5.9,解得x=60,95﹣x=95﹣60=35.
答:小李家12月使用“峰时”用电60度,谷时用电35度.
【点睛】本题考查了统计表、一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
20.(2020秋?历城区期末)小强是校学生会体育部部长,他想了解现在同学们更喜欢什么球类运动,以便学生会组织比赛,小强随机调查了300名同学,调在结果如下表:
最喜欢的球类运动
篮球
足球
排球
乒乓球
羽毛球
其他
人数
68
m
27
90
36
9
(1)本次调查结果中喜欢足球运动项目的人数m= ;
(2)本次调查结果中喜欢排球运动项目的人数占调查总人数的百分比是 ;
(3)根据调查数据,在绘制扇形统计图的过程中,羽毛球所对应扇形的圆心角度数等于 °;
(4)如果你是体育部长,根据调查的结果,你会组织什么比赛?说说你的理由.
【分析】(1)根据题意和表格中的数据,可以计算出m的值;(2)根据表格中的数据,可以计算出本次调查结果中喜欢排球运动项目的人数占调查总人数的百分比;(3)根据表格中的数据可以计算出羽毛球所对应扇形的圆心角度数;(4)本题答案不唯一,只要合理即可.
【解答】解:(1)由表格可得,m=300﹣68﹣27﹣90﹣36﹣9=70,故答案为:70;
(2)本次调查结果中喜欢排球运动项目的人数占调查总人数的百分比是100%=9%,
故答案为:9%;
(3)羽毛球所对应扇形的圆心角度数为:360°108°,故答案为:108;
(4)组织乒乓球比赛、篮球比赛和足球比赛,理由:由表格可知,喜欢乒乓球、足球和篮球的学生比较多,故可以组织乒乓球比赛、篮球比赛和足球比赛.
【点睛】本题考查扇形统计图,解答本题的关键是明确题意,利用扇形统计图的知识解答.
21.(2021·河南南阳市·九年级一模)2020年国家提出并部署了“新基建”项目,主要包含“特高压,城际高速铁路和城市轨道交通,5G基站建设,工业互联网,大数据中心,人工智能,新能源汽车充电桩”等.《2020新基建中高端人才市场就业吸引力报告》重点刻画了“新基建”中五大细分领域(5G基站建设,工业互联网,大数据中心,人工智能,新能源汽车充电桩)总体的人才与就业机会.下图是其中的一个统计图.
请根据图中信息,解答下列问题:
(1)图中2020年“新基建”七大领域预计投资规模的平均数约是________亿元(结果保留一位小数);
(2)在由“新基建”七大领域预计投资规模组成的扇形统计图中,“新能源汽车充电桩”预计投资规模所占的圆心角约是_______(结果保留整数);(3)甲,乙两位待业人员,仅根据上面统计图中的数据,从五大细分领域中,甲选择了“5G基站建设”,乙选择了“人工智能”分别作为自己的就业方向,请简要说明他们选择就业方向的理由各是什么.
【答案】(1)314.6;(2)49;(3)甲更关注在线职位增长率;乙关注的是2020年预计投资规模最大
【分析】(1)按照求平均数的公式计算即可,即把七大领域预计投资规模数相加并除以7,就可得平均数;
(2)计算“新能源汽车充电桩”预计投资规模在七大领域预计投资规模总数中的百分数,它与360°的积就是所求扇形的圆心角;(3)观察统计图知,“5G基站建设”
在线职位增长率最大,故甲关注它;而“人工智能”则是五大细分领域中2020年预计投资规模最大的,故乙关注它.
【详解】(1)2020年“新基建”七大领域预计投资规模的平均数为:
(100+640+300+200+160+500+300)÷7≈314.3(亿元)故答案为:314.3
(2)故答案为:49
(3)五大细分领域中,“5G基站建设”
在线职位与2019年同期相比,增长率最大,所以甲关注的是这个增长率;而“人工智能”则是五大细分领域中2020年预计投资规模最大的,故乙关注它.
【点睛】本题综合考查了各种统计图,关键是读懂统计图,获取所需要的信息.
22.(2020·北京大兴初三一模)新冠肺炎疫情暴发后,一场同时间赛跑、与病魔较量的战役随即打响.在疫情防控一线,除了广大医务工作者义无反顾、日夜奋战之外,在另一条战线上,科研人员也在加班加点、紧急攻关.全国科技战线积极响应党中央号召,科技、卫健等12个部门组成科研攻关组,短短一个月的时间内就取得了积极进展.3月13日0﹣24时,31个省(自治区、直辖市)和新疆生产建设兵团新增确诊病例11例(数据不含港澳台),新增疑似病例17例(数据不含港澳台).如图是根据国家卫健委关于新型冠状病毒肺炎通报的数据(数据不含港澳台)绘制的统计图:
根据以上信息,回答下列问题:
(1)下列推断合理的是_______.
①2月15日武汉新增确诊病例约为1500例;②从2月23日起到3月13日止,武汉每日新增确诊病例都在500例以下;③从2月23日起到3月13日止,全国每日新增疑似病例逐渐减少.④3月13日湖北新增疑似病例不超过17例.
(2)结合本题的信息及当前防疫形势,说说你的感受.
【答案】(1)①④;(2)见解析.
【分析】(1)利用图中信息一一判断即可.(2)结合本题的信息及当前防疫形势,说说自己的感受即可.
【解析】(1)由图中信息可知:①2月15日武汉新增确诊病例约为1500例,正确.
②从2月23日起到3月13日止,武汉每日新增确诊病例都在500例以下,错误,2月24日前每日新增确诊病例都在500以上.③从2月23日起到3月13日止,全国每日新增疑似病例逐渐减少.错误,其中2月18日到2月20日是逐渐增加的.④3月13日湖北新增疑似病例不超过17例.正确.故答案为①④.
(2)国内疫情防控科学有效,防控形势持续向好.相信中国一定能打赢这场战疫.
【点睛】本题考查折线统计图,解题的关键是读懂图象信息,属于中考常考题型.
23.(2020·北京通州初三一模)国务院发布的《全民科学素质行动计划纲要实施方案(2016-2020年)》指出:公民科学素质是实施创新驱动发展战略的基础,是国家综合国力的体现.《方案》明确提出,2020年要将我国公民科学素质的数值提升到10%以上.为了解我国公民科学素质水平及发展状况,中国科协等单位已多次组织了全国范围的调查,以下是根据调查结果整理得到的部分信息.注:科学素质的数值是指具备一定科学素质的公民人数占公民总数的百分比.
.2015和2018年我国各直辖市公民科学素质发展状况统计图如下:
2015年
2018年
男
女
b.2015年和2018年我国公民科学素质发展状况按性别分类统计如下:
c.2001年以来我国公民科学素质水平发展统计图如下:
根据以上信息,回答下列问题:
(1)在我国四个直辖市中,从2015年到2018年,公民科学素质水平增幅最大的城市是________,公民科学素质水平增速最快的城市是_________.注:科学素质水平增幅=2018年科学素质的数值一2015年科学素质的数值;科学素质水平增速=(2018年科学素质的数值一2015年科学素质的数值)÷2015年科学素质的数值.
(2)已知在2015年的调查样本中,男女公民的比例约为1:1,则2015年我国公民的科学素质水平为______%(结果保留一位小数);由计算可知.在2018年的调查样本中.男性公民人数_____女性公民人数(填“多于”、“等于”或“少于”).(3)根据截至2018年的调查数据推断,你认为“2020年我国公民科学素质提升到10%以上”的目标能够实现吗?请说明理由.
【答案】(1)北京,重庆;(2)6.2,少于;(3)见解析
【分析】(1)利用条形统计图中信息判断即可.(2)利用表格和折线统计图信息,解决问题即可.
(3)答案不唯一,说法合理即可.
【解析】解:(1)由2015和2018年我国各直辖市公民科学素质发展状况统计图如图1得知,
上海:22%-19%=3%,北京:21.5%-17.5%=4%,天津:14%-12%=2%,重庆:8%-4.5%=3.5%,
故在我国四个直辖市中,从2015年到2018年,公民科学素质水平增幅最大的城市是北京;
上海:3%÷19%≈16%,北京:4%÷21.5%≈19%,天津:2%÷12%≈17%,重庆:3.5%÷4.5%=78%,
故公民科学素质水平增速最快的城市是重庆;故答案为:北京,重庆;
(2)∵在2015年的调查样本中,男女公民的比例约为1:1,
∴2015年我国公民的科学素质水平为(9.0%+3.4%)÷2=6.2%,
设男性公民占x%,则有11.1%×x%+6.2%×(1-x%)=8.5%,解得x=47,
∴男性公民人数少于女性公民人数,故答案为6.2,少于.
(3)①能实现.理由如下:
2015年我国公民的科学素质水平为6.2%,2018年我国公民的科学素质水平为8.5%,平均每年的增幅平均为0.77%,
如果按照匀速增长的速度推断,2020年我国公民的科学素质水平达到10.3%,
由此可知,“2020年我国公民科学素质提升到10%以上”的目标能够实现.
②条件不足,无法判断.理由如下:一种情形同①,能实现目标.另一种情形,无法判断.
因为不知道2018~2020年间我国公民的科学素质水平的增从速度是加快还是减缓,所以无法判断,2020年能否实现目标.
【点睛】本题考查条形统计图,统计表,折线统计图等知识,解题的关键是理解题意,读懂图象信息,属于中考常考题型.
24.(2019·浙江江干初二期末)为了节约能源,某城市开展了节约水电活动,已知该城市共有10000户家庭,活动前,某调查小组随机抽取了部分家庭每月的水电费的开支(单位:元),结果如左图所示频数直方图(每一组含前一个边界值,不含后一个边界值);活动后,再次调查这些家庭每月的水电费的开支,结果如表所示:
(1)求所抽取的样本的容量;(2)如以每月水电费开支在225元以下(不含)为达到节约标准,请问通过本次活动,该城市大约增加了多少户家庭达到节约标准?(3)活动后,这些样本家庭每月水电费开支的总额能否低于6000元?(4)请选择一个适当的统计量分析活动前后的相关数据,并评价节约水电活动的效果.
【答案】(1)40;(2)1250户;(3)活动后,这些样本家庭每月水电费开支的总额不低于6000元.(4)开支在225以下的户数上可以看出节约水电活动的效果还不错.
【分析】(1)将频数分布直方图各分组频数相加即可得样本容量;
(2)分别计算出活动前、后达到节约标准的家庭数,相减即可得;
(3)取各分组的组中值,再分别乘以各分组的频数,相加即可得;
(4)根据统计图中的数据可以解答本题,本题答案不唯一,只要合理即可..
【解析】解:(1)所抽取的样本的容量为6+12+11+7+3+1=40;
(2)活动前达到节约标准的家庭数为10000×=7250(户),
活动后达到节约标准的家庭数为10000×=8500(户),85007250=1250(户),
∴该城市大约增加了1250户家庭达到节约标准;
(3)这40户家庭每月水电费开支总额为:
7×100+13×150+14×200+4×250+2×300=7050(元),
∴活动后,这些样本家庭每月水电费开支的总额不低于6000元.
(4)根据题意可知,开支在225以下的户数上可以看出节约水电活动的效果还不错.
【点睛】本题考查的是频数分布直方图的运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.频数分布直方图能清楚地表示出每个项目的数据.
25.(2021·山东济南市·九年级一模)加强劳动教育是学校贯彻“五育并举”的重要举措.为了解学生参加各项劳动的情况,某校对七年级部分学生进行了随机问卷调查,其中一个问题是“你每周在家参加家务劳动的时间是多少?”,共有如下四个选项:
A.1小时以下
B.1~2小时(不包含2小时)
C.2~3小时(包含2小时)
D.3小时以上
图①、图②是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
(1)填空:本次问卷调查一共调查了______名学生;(2)请将图①的条形统计图补充完整;
(3)并求出图②中D部分所对应的圆心角度数;(4)若该校共有1800名学生,请你估计全校可能有多少名学生每周在家参加家务劳动的时间在2小时以上(包含2小时)?
【答案】(1)200;(2)见解析;(3);(4)估计全校可能有360名学生每周在家参加家务劳动的时间在2小时以上(包含2小时)
【分析】(1)根据B选项人数及其占被调查人数的比例计算即可得出答案.(2)用总人数减去其他选项的人数求出D选项的人数,即可补全统计图;(3)用乘以D部分所占的百分比即可得出D部分所对应的圆心角度数;(4)用该校的总人数乘以每周在家参加家务劳动的时间在2小时以上(包含2小时)的人数所占的百分比即可.
【详解】解:(1)本次问卷调查一共调查的学生数是:(名)故答案为:200;
(2)劳动的时间在3小时以上的人数有:(名),补全统计图如下:
(3)D部分所对应的圆心角度数是;
(4)根据题意得:(名),
答:估计全校可能有360名学生每周在家参加家务劳动的时间在2小时以上(包含2小时).
【点睛】本题考查条形统计图、扇形统计图等知识,解题的关键是熟练掌握基本概念,学会用样本估计总体的思想解决问题,属于基础题,中考常考题型.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
