第16章第3节二次根式的运算及其应用-期末总复习 2020-2021学年人教版数学八年级下册(Word版含答案)
文档属性
| 名称 | 第16章第3节二次根式的运算及其应用-期末总复习 2020-2021学年人教版数学八年级下册(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 430.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-04 10:18:08 | ||
图片预览




文档简介
2020-2021人教版八年级下册第16章第3节二次根式的运算及其应用-期末总复习
1.下列运算正确的是( )
A.
B.
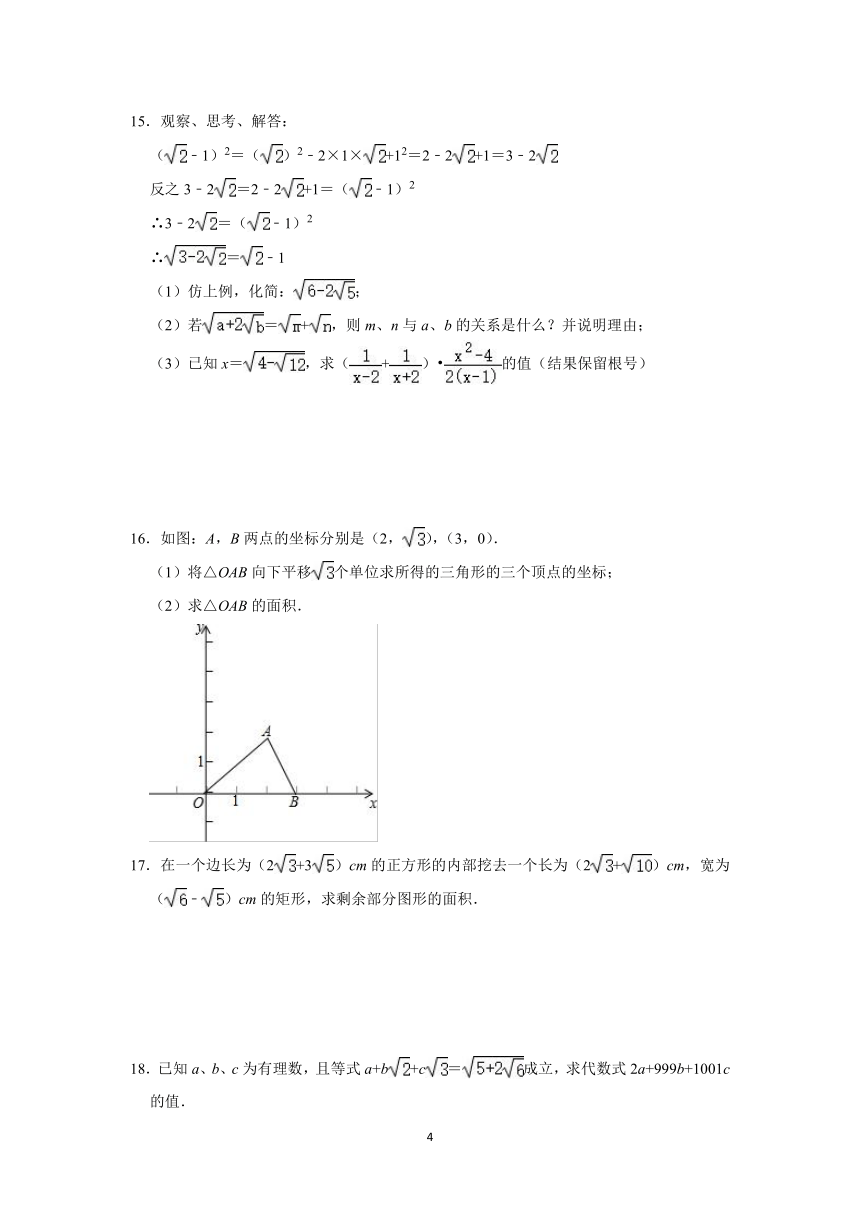
C.
D.
2.下列计算正确的是( )
A.
B.
C.
D.
3.设x、y都是负数,则等于( )
A.
B.
C.
D.
4.下列计算:①()2=2,②=﹣2,③(﹣2)2=12,④=2,⑤﹣=,⑥()(﹣)=﹣1,其中结果正确的个数为( )
A.1
B.2
C.3
D.4
5.已知1<x<2,,则的值是
.
6.设a﹣b=2+,b﹣c=2﹣,则a2+b2+c2﹣ab﹣ac﹣bc=
.
7.已知xy=3,那么的值是
.
8.计算:
(1)(﹣3)﹣(﹣)
(2)+2
(3)(+)(﹣)+(2+3)2
(4)(4﹣2+3)÷.
9.已知:,,求代数式x2﹣xy+y2值.
10.已知线段a,b,c,且线段a,b满足|a﹣|+(b﹣)2=0.
(1)求a,b的值;
(2)若a,b,c是某直角三角形的三条边的长度,求c的值.
11.已知长方形的长a=,宽b=.
(1)求长方形的周长;
(2)求与长方形等面积的正方形的周长,并比较与长方形周长的大小关系.
12.阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2=(1+)2,善于思考的小明进行了以下探索:
设a+b=(m+n)2(其中a、b、m、n均为整数),则有a+b=m2+2n2+2mn.
∴a=m2+2n2,b=2mn.这样小明就找到了一种把部分a+b的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b=(m+n)2,用含m、n的式子分别表示a、b,得a=
,b=
;
(2)试着把7+4化成一个完全平方式.
(3)若a是216的立方根,b是16的平方根,试计算:.
13.在学习了“二次根式”后,李梅在练习册上遇到了下列这道题,请你帮李梅完成该题.
一个长方体的塑料容器中装满水,该塑料容器的底面是边长为cm的正方形,现将塑料容器的一部分水倒入一个高为cm的圆柱形玻璃容器中,当玻璃容器装满水时,塑料容器中的水面下降了cm(提示:圆柱的体积=πr2h,其中,r为底面的半径,h为高,π取3)
(1)求从塑料容器中倒出的水的体积;
(2)求圆柱形玻璃容器的底面的半径.
14.探究过程:观察下列各式及其验证过程.
(1)2=(2)3=
验证:2=×=====
验证:3=×=====
(1)按照上面两个等式及其验证过程的基本思路,猜想:4=
;5=
;
(2)通过上述探究你能猜测出:n=
(n>0),并验证你的结论.
15.观察、思考、解答:
(﹣1)2=()2﹣2×1×+12=2﹣2+1=3﹣2
反之3﹣2=2﹣2+1=(﹣1)2
∴3﹣2=(﹣1)2
∴=﹣1
(1)仿上例,化简:;
(2)若=+,则m、n与a、b的关系是什么?并说明理由;
(3)已知x=,求(+)?的值(结果保留根号)
16.如图:A,B两点的坐标分别是(2,),(3,0).
(1)将△OAB向下平移个单位求所得的三角形的三个顶点的坐标;
(2)求△OAB的面积.
17.在一个边长为(2+3)cm的正方形的内部挖去一个长为(2+)cm,宽为(﹣)cm的矩形,求剩余部分图形的面积.
18.已知a、b、c为有理数,且等式a+b+c=成立,求代数式2a+999b+1001c的值.
19.已知x=+,y=+,比较x与y的大小.
20.已知a、b满足+=0,求2a(÷)
21.像(+2)(﹣2)=1、?=a(a≥0)、(+1)(﹣1)=b﹣1(b≥0)……两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.例如,与,+1与﹣1,2+3与2﹣3等都是互为有理化因式.进行二次根式计算时,利用有理化因式,可以化去分母中的根号.请完成下列问题:
(1)化简:;
(2)计算:+;
(3)比较﹣与﹣的大小,并说明理由.
22.小静设计了一幅矩形图片,已知矩形的长,宽为,她又想设计一个面积相等的圆,请你帮助小静求出圆的半径.
23.观察下列各式:;;…,
请你猜想:
(1)=
,=
.
(2)计算(请写出推导过程):
(3)请你将猜想到的规律用含有自然数n(n≥1)的代数式表达出来
.
24.数学活动课上,张老师说:“是无理数,无理数就是无限不循环小数,同学们,你能把的小数部分全部写出来吗?”大家议论纷纷,晶晶同学说:“要把它的小数部分全部写出来是非常难的,但我们可以用(﹣1)表示它的小数部分.接着,张老师出示了一道练习题:
“已知8+=x+y,其中x是一个整数,且0<y<1,请你求出2x+(﹣y)2016的值”.请聪明的你给出正确答案.
25.细心观察图形,认真分析各式,然后解答问题:
OA1=1;
OA2==;
S1=×1×1=;
OA3==; S2=××1=;
OA4==; S3=××1=;
(1)推算出OA10=
.
(2)若一个三角形的面积是.则它是第
个三角形.
(3)用含n(n是正整数)的等式表示上述面积变化规律;
(4)求出S12+S22+S23+…+S2100的值.
参考答案
1.D
2.D
3.D
4.C
5.﹣2
6.15
7.±2
8.解:(1)原式=2﹣﹣+3
=+;
(2)原式=﹣+2
=3﹣2+2
=3;
(3)原式=2﹣3+8+12+27
=34+12;
(4)原式=(4﹣4+9)÷
=9?
=9.
9.解:x2﹣xy+y2=(x﹣y)2+xy,
当,,
原式=(2)2+7﹣5=22.
10.解:(1)因为线段a,b满足|a﹣|+(b﹣)2=0.
所以a=4,b=;
(2)因为a,b,c是某直角三角形的三条边的长度,
所以c=或.
11.解:a==2,b==.
(1)长方形的周长=(2+)×2=6;
(2)正方形的周长=4=8,
∵6=.8=,
∵>
∴6>8.
12.解:(1)a+b=(m+n)2,
∵a+b=m2+3n2+2mn,
∴a=m2+3n2,b=2mn,
故答案为:m2+3n2;2mn;
(2)7+4=(2+)2;
(3)∵a是216的立方根,b是16的平方根,
∴a=6,b=±4,
∴===2±.
13.解:(1)由题意可得:
××=448(cm3).
答:从塑料容器中倒出的水的体积为448cm3;
(2)设圆柱形玻璃容器的底面的半径为r,根据题意可得:
π×r2×=448,
解得:r=.
答:圆柱形玻璃容器的底面的半径为cm.
14.解:(1)4=;5=;
(2)n=(n>0),
验证:n=?====(n>0).
故答案为;;.
15.解:(1)=;
(2)a=m+n,b=mn,
理由:∵=+,
∴,
∴a=m+n,b=mn;
(3)∵x==,
∴(+)?
=
=
=
=
=
=
=﹣1﹣.
16.解:(1)
∴所得的三角形的三个顶点的坐标为A′(2,0),O′(0,﹣),B′(3,﹣);
(2)△OAB的面积=×3×=.
17.解:剩余部分的面积为:(2+3)2﹣(2+)(﹣)=(12+12+45)﹣(6﹣2+2﹣5)=(57+12﹣)(cm2).
18.解:∵==+,
∴a+b+c=+,
又∵a、b、c为有理数,
∴a=0,b=1,c=1,
∴2a+999b+1001c=2000.
19.解:x2=12+2、y2=12+2,
因为大于,
所以
x>y.
20.解:根据题意,得:,
解得:,
故2a(÷)
=2×(﹣1)×(÷)
=﹣2×(×)
=﹣2×3
=﹣6.
21.解:(1)==;
(2)+
=2++
=2+2+;
(3)﹣<﹣,
理由:∵﹣=,
﹣=,
,
∴<,
∴﹣<﹣.
22.解:设圆的半径为R,
根据题意得πR2=?,即πR2=2π??,
解得R1=,R2=﹣(舍去),
所以所求圆的半径为cm.
23.解:(1),;
(2);
(3)(n≥1).
24.解:∵1<<2,
∴9<8+<10,
∵8+=x+y,其中x是一个整数,且0<y<1,
∴x=9,y=8+﹣9=﹣1,
∴2x+(﹣y)2016=2×9+[﹣(﹣1)]2016=18+1=19.
25.解:(1))∵OAn2=n,
∴OA10=.
故答案为:;
(2)若一个三角形的面积是,
∵Sn==,
∴=2=,
∴它是第20个三角形.
故答案为:20;
(3)结合已知数据,可得:OAn2=n;Sn=;
(4)S12+S22+S23+…+S2100
=++++…+
=
=
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2021/5/25
15:20:59;用户:数学3;邮箱:zz4z368@;学号:25212959
1.下列运算正确的是( )
A.
B.
C.
D.
2.下列计算正确的是( )
A.
B.
C.
D.
3.设x、y都是负数,则等于( )
A.
B.
C.
D.
4.下列计算:①()2=2,②=﹣2,③(﹣2)2=12,④=2,⑤﹣=,⑥()(﹣)=﹣1,其中结果正确的个数为( )
A.1
B.2
C.3
D.4
5.已知1<x<2,,则的值是
.
6.设a﹣b=2+,b﹣c=2﹣,则a2+b2+c2﹣ab﹣ac﹣bc=
.
7.已知xy=3,那么的值是
.
8.计算:
(1)(﹣3)﹣(﹣)
(2)+2
(3)(+)(﹣)+(2+3)2
(4)(4﹣2+3)÷.
9.已知:,,求代数式x2﹣xy+y2值.
10.已知线段a,b,c,且线段a,b满足|a﹣|+(b﹣)2=0.
(1)求a,b的值;
(2)若a,b,c是某直角三角形的三条边的长度,求c的值.
11.已知长方形的长a=,宽b=.
(1)求长方形的周长;
(2)求与长方形等面积的正方形的周长,并比较与长方形周长的大小关系.
12.阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2=(1+)2,善于思考的小明进行了以下探索:
设a+b=(m+n)2(其中a、b、m、n均为整数),则有a+b=m2+2n2+2mn.
∴a=m2+2n2,b=2mn.这样小明就找到了一种把部分a+b的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b=(m+n)2,用含m、n的式子分别表示a、b,得a=
,b=
;
(2)试着把7+4化成一个完全平方式.
(3)若a是216的立方根,b是16的平方根,试计算:.
13.在学习了“二次根式”后,李梅在练习册上遇到了下列这道题,请你帮李梅完成该题.
一个长方体的塑料容器中装满水,该塑料容器的底面是边长为cm的正方形,现将塑料容器的一部分水倒入一个高为cm的圆柱形玻璃容器中,当玻璃容器装满水时,塑料容器中的水面下降了cm(提示:圆柱的体积=πr2h,其中,r为底面的半径,h为高,π取3)
(1)求从塑料容器中倒出的水的体积;
(2)求圆柱形玻璃容器的底面的半径.
14.探究过程:观察下列各式及其验证过程.
(1)2=(2)3=
验证:2=×=====
验证:3=×=====
(1)按照上面两个等式及其验证过程的基本思路,猜想:4=
;5=
;
(2)通过上述探究你能猜测出:n=
(n>0),并验证你的结论.
15.观察、思考、解答:
(﹣1)2=()2﹣2×1×+12=2﹣2+1=3﹣2
反之3﹣2=2﹣2+1=(﹣1)2
∴3﹣2=(﹣1)2
∴=﹣1
(1)仿上例,化简:;
(2)若=+,则m、n与a、b的关系是什么?并说明理由;
(3)已知x=,求(+)?的值(结果保留根号)
16.如图:A,B两点的坐标分别是(2,),(3,0).
(1)将△OAB向下平移个单位求所得的三角形的三个顶点的坐标;
(2)求△OAB的面积.
17.在一个边长为(2+3)cm的正方形的内部挖去一个长为(2+)cm,宽为(﹣)cm的矩形,求剩余部分图形的面积.
18.已知a、b、c为有理数,且等式a+b+c=成立,求代数式2a+999b+1001c的值.
19.已知x=+,y=+,比较x与y的大小.
20.已知a、b满足+=0,求2a(÷)
21.像(+2)(﹣2)=1、?=a(a≥0)、(+1)(﹣1)=b﹣1(b≥0)……两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.例如,与,+1与﹣1,2+3与2﹣3等都是互为有理化因式.进行二次根式计算时,利用有理化因式,可以化去分母中的根号.请完成下列问题:
(1)化简:;
(2)计算:+;
(3)比较﹣与﹣的大小,并说明理由.
22.小静设计了一幅矩形图片,已知矩形的长,宽为,她又想设计一个面积相等的圆,请你帮助小静求出圆的半径.
23.观察下列各式:;;…,
请你猜想:
(1)=
,=
.
(2)计算(请写出推导过程):
(3)请你将猜想到的规律用含有自然数n(n≥1)的代数式表达出来
.
24.数学活动课上,张老师说:“是无理数,无理数就是无限不循环小数,同学们,你能把的小数部分全部写出来吗?”大家议论纷纷,晶晶同学说:“要把它的小数部分全部写出来是非常难的,但我们可以用(﹣1)表示它的小数部分.接着,张老师出示了一道练习题:
“已知8+=x+y,其中x是一个整数,且0<y<1,请你求出2x+(﹣y)2016的值”.请聪明的你给出正确答案.
25.细心观察图形,认真分析各式,然后解答问题:
OA1=1;
OA2==;
S1=×1×1=;
OA3==; S2=××1=;
OA4==; S3=××1=;
(1)推算出OA10=
.
(2)若一个三角形的面积是.则它是第
个三角形.
(3)用含n(n是正整数)的等式表示上述面积变化规律;
(4)求出S12+S22+S23+…+S2100的值.
参考答案
1.D
2.D
3.D
4.C
5.﹣2
6.15
7.±2
8.解:(1)原式=2﹣﹣+3
=+;
(2)原式=﹣+2
=3﹣2+2
=3;
(3)原式=2﹣3+8+12+27
=34+12;
(4)原式=(4﹣4+9)÷
=9?
=9.
9.解:x2﹣xy+y2=(x﹣y)2+xy,
当,,
原式=(2)2+7﹣5=22.
10.解:(1)因为线段a,b满足|a﹣|+(b﹣)2=0.
所以a=4,b=;
(2)因为a,b,c是某直角三角形的三条边的长度,
所以c=或.
11.解:a==2,b==.
(1)长方形的周长=(2+)×2=6;
(2)正方形的周长=4=8,
∵6=.8=,
∵>
∴6>8.
12.解:(1)a+b=(m+n)2,
∵a+b=m2+3n2+2mn,
∴a=m2+3n2,b=2mn,
故答案为:m2+3n2;2mn;
(2)7+4=(2+)2;
(3)∵a是216的立方根,b是16的平方根,
∴a=6,b=±4,
∴===2±.
13.解:(1)由题意可得:
××=448(cm3).
答:从塑料容器中倒出的水的体积为448cm3;
(2)设圆柱形玻璃容器的底面的半径为r,根据题意可得:
π×r2×=448,
解得:r=.
答:圆柱形玻璃容器的底面的半径为cm.
14.解:(1)4=;5=;
(2)n=(n>0),
验证:n=?====(n>0).
故答案为;;.
15.解:(1)=;
(2)a=m+n,b=mn,
理由:∵=+,
∴,
∴a=m+n,b=mn;
(3)∵x==,
∴(+)?
=
=
=
=
=
=
=﹣1﹣.
16.解:(1)
∴所得的三角形的三个顶点的坐标为A′(2,0),O′(0,﹣),B′(3,﹣);
(2)△OAB的面积=×3×=.
17.解:剩余部分的面积为:(2+3)2﹣(2+)(﹣)=(12+12+45)﹣(6﹣2+2﹣5)=(57+12﹣)(cm2).
18.解:∵==+,
∴a+b+c=+,
又∵a、b、c为有理数,
∴a=0,b=1,c=1,
∴2a+999b+1001c=2000.
19.解:x2=12+2、y2=12+2,
因为大于,
所以
x>y.
20.解:根据题意,得:,
解得:,
故2a(÷)
=2×(﹣1)×(÷)
=﹣2×(×)
=﹣2×3
=﹣6.
21.解:(1)==;
(2)+
=2++
=2+2+;
(3)﹣<﹣,
理由:∵﹣=,
﹣=,
,
∴<,
∴﹣<﹣.
22.解:设圆的半径为R,
根据题意得πR2=?,即πR2=2π??,
解得R1=,R2=﹣(舍去),
所以所求圆的半径为cm.
23.解:(1),;
(2);
(3)(n≥1).
24.解:∵1<<2,
∴9<8+<10,
∵8+=x+y,其中x是一个整数,且0<y<1,
∴x=9,y=8+﹣9=﹣1,
∴2x+(﹣y)2016=2×9+[﹣(﹣1)]2016=18+1=19.
25.解:(1))∵OAn2=n,
∴OA10=.
故答案为:;
(2)若一个三角形的面积是,
∵Sn==,
∴=2=,
∴它是第20个三角形.
故答案为:20;
(3)结合已知数据,可得:OAn2=n;Sn=;
(4)S12+S22+S23+…+S2100
=++++…+
=
=
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2021/5/25
15:20:59;用户:数学3;邮箱:zz4z368@;学号:25212959
