1.2.1函数的概念

(共18张PPT)
2.1函数的概念与性质
在一个变化过程中,有两个变量x和y，如果给定一个x值，相应地就确定唯一的一个y值, 那么就称y是x的函数，其中x是自变量,y是因变量.
1.函数（传统）定义
2.1.1 函数的概念与性质
　　物体从静止开始下落，下落的距离随时间的变化而变化.
　　下落的距离h(m)与时间t(s)之间近似地满足关系式
h＝ tx2.
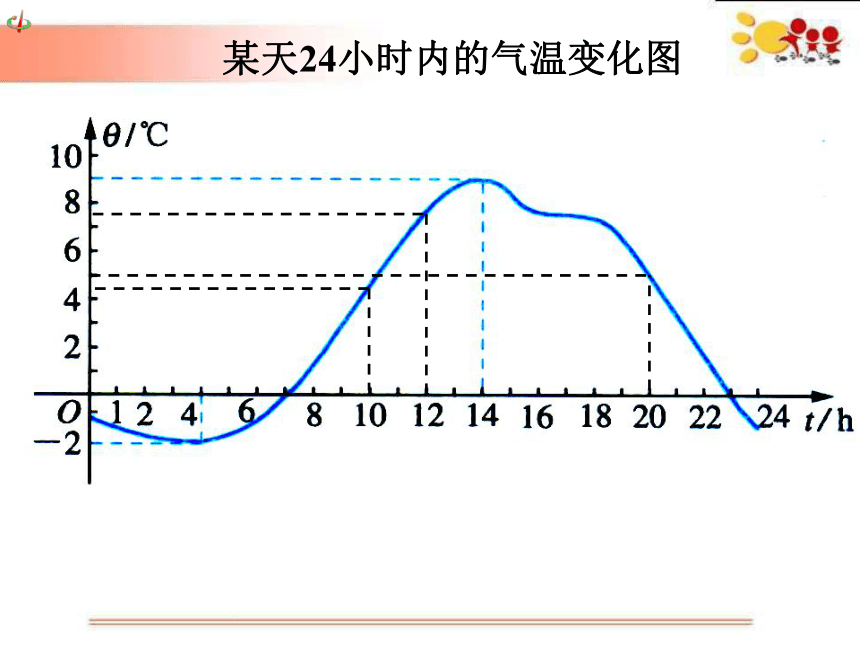
某天24小时内的气温变化图
学号 1 2 3 4 5
成绩 80 82 82 82 85
1
2
3
4
5
80
82
85
某班级学号为1-5的学生参加数学测试的成绩表
设集合A是一个非空的数集，对A中的任意数x , 按照确定的法则f，都有唯一确定的数y与它对应, 则这种对应关系叫做集合A上的一个函数．记作：
y＝f (x)，x A
其中x叫做自变量，自变量的取值范围（数集A）叫做这个函数的定义域。
2.函数(集合语言 )定义
如果自变量取值 a，则由法则 f 确定的值 y 称为函数在 a 处的函数值，记作：
y=f(a) 或 y|x=a
所有函数值构成的集合 {y|y=f (x),x∈A} 叫做这个函数的值域。
函数y=f (x)也经常写作函数 f 或函数f (x)
判断下列对应是否为数集A到数集B的一个函数：
(2) A=B=[0,+∞)，x→y，y是x的算术平方根．
(1) A={ 1,2,3,4,5}，B={2,4,6,8}，f(x)=2x.
(4) A={1,2,3}，B={7,8,9}，f(1)=f(2)=7，f(3)=8．
(3) A=[0,+∞) ，B=R，x→y，y是x的平方根．
√
×
×
√
练习：下列各图中，可表示函数y＝f（x）的图
象的只可能是（　　）
D
定义域A； 对应法则 f.
3. 函数的二要素:
(2) f 表示对应法则，不同函数中f 的具体含义不一样；
(1)函数符号y＝f (x) 表示y是x的函数， f (x)不是表示 f 与x的乘积；
说明：
(3)“y=f (x)”是函数符号，可以用任意的字母表示，如：“y=g(x)”;
函数
定义域
值域
对应关系
值域是由定义域和对应关系决定的.
如果两个函数的定义域和对应关系完全一致，
就称这两个函数相等
4.函数相等
⑴
⑵
⑶
⑷
当定义域和对应法则完全一致时,两个函数
才相同.
√
5.已学函数的定义域和值域
定义域R，值域R.
定义域{x|x≠0}，值域{y|y≠0}.
⑴ 一次函数f(x)＝ax＋b(a≠0)
⑵
⑶二次函数f(x)＝ax2＋bx＋c (a≠0)
定义域：R，
值域：
当a＞0时，
当a＜0时，
5.已学函数的定义域和值域
⒈满足不等式a≤x≤b的实数x的集合叫做闭区间，
表示为[a，b]
设a，b是两个实数，而且a⒉满足不等式a表示为(a，b)
⒊满足不等式a≤x半开半闭区间，表示为[a，b）或（a，b]
这里的实数a，b叫做相应区间的端点
7.区间的概念
4.无穷区间：表示为（- ∞，+ ∞ ）
集合表示
区间表示
数轴表示
{x a＜x＜b}
(a , b)
。
。
{x a≤x≤b}
[a , b]
.
.
{x a≤x＜b}
[a , b)
.
。
{x a＜x≤b}
(a , b]
.
。
{x x＜a}
(－∞, a)
。
{x x≤a}
(－∞, a]
.
{x x＞b}
(b , +∞)
。
{x x≥b}
[b , +∞)
.
{x x∈R}
(－∞,+∞)
数轴上所有的实数
课堂小结
1.函数概念
2.函数的两要素
3.区间的概念