2.1.3函数的单调性

(共21张PPT)
函数的单调性
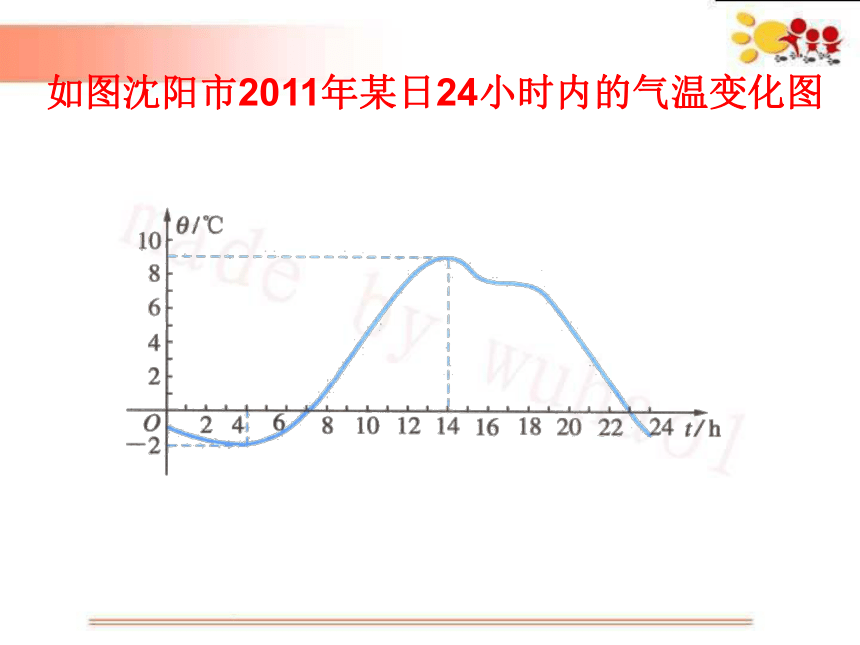
如图沈阳市2011年某日24小时内的气温变化图
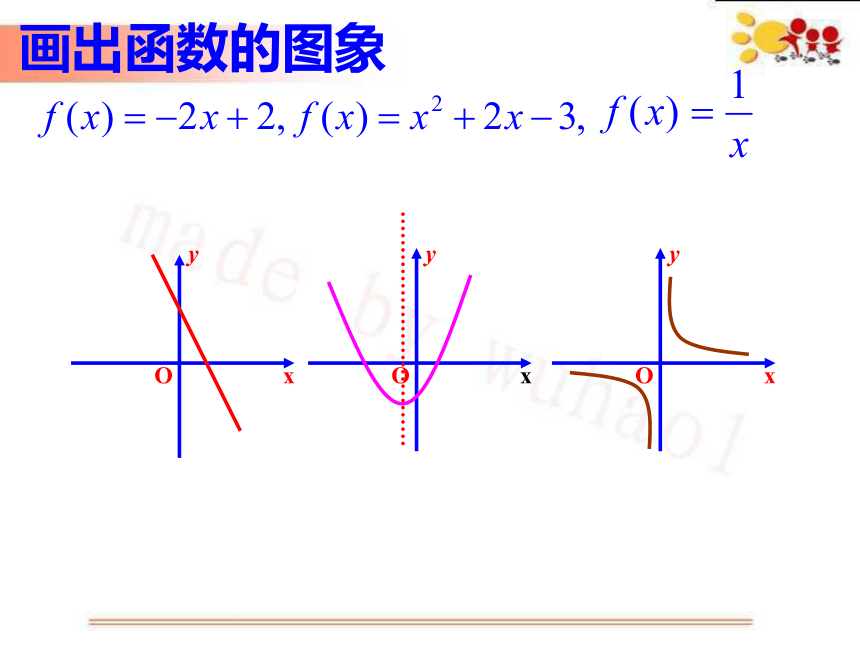
画出函数的图象
x
y
O
x
y
O
x
y
O
A
B
自变量x的改变量
函数值y的改变量
------
------
1、增函数与减函数
增函数
减函数
1、增函数与减函数定义
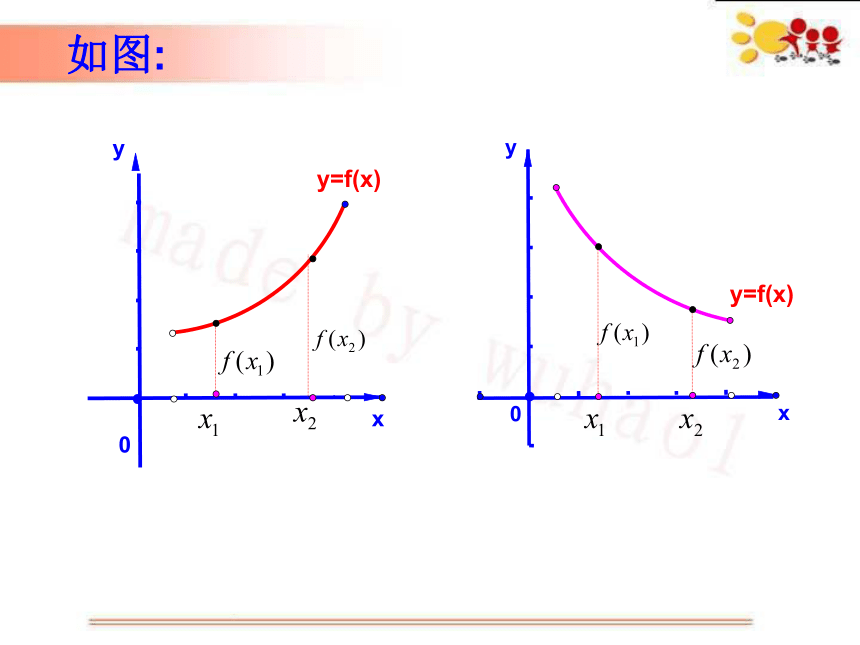
如图:
y=f(x)
0
y
x
y=f(x)
0
y
x
如果一个函数在某个区间M上是增函数
或是减函数，
具有
(区间称为单调区间．)
就说这个函数在这个区间M上
单调性．
2、单调性、单调区间
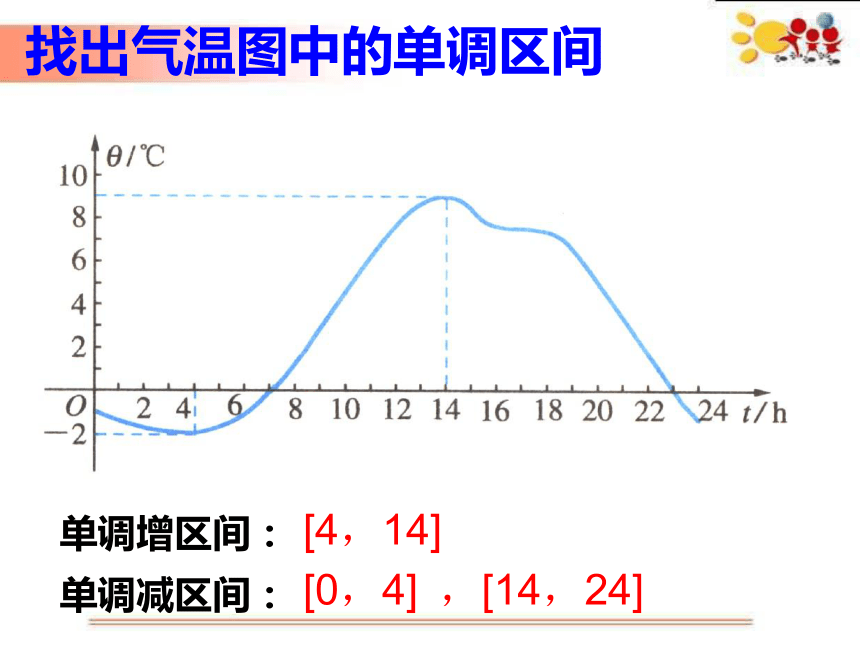
单调增区间：
单调减区间：
[4，14]
[0，4]
，[14，24]
找出气温图中的单调区间
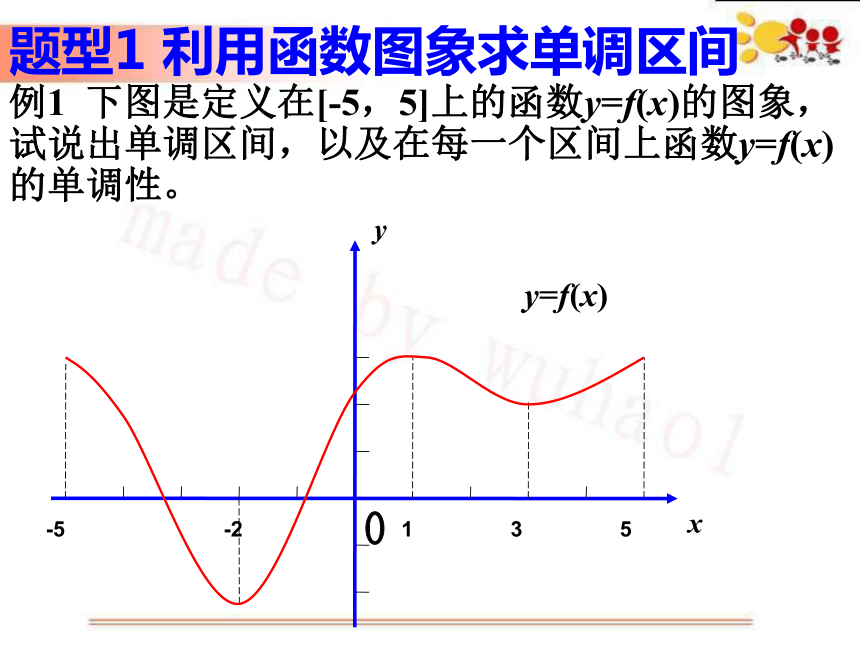
题型1 利用函数图象求单调区间
例1 下图是定义在[-5，5]上的函数y=f(x)的图象，试说出单调区间，以及在每一个区间上函数y=f(x)的单调性。
1
-5
-2
5
3
x
y
y=f(x)
例2 求函数f(x)=|x2-2x-3|的单调区。
题型1 利用函数图象求单调区间
-5
-4
-3
-2
-1
0
1
2
3
4
5
y
x
已知函数的图象（包括端点），根据图象说出函数的单调区间，以及在每一个区间 上，函数是增函数还是减函数．
练习1
-3
6
1.5
-1.5
3
y=g(x)
y
x
3.特别提示
(1)单调性是与“区间”紧密相关的概念，一个函数在不同的区间上可以有不同的单调性；
(2)单调性是函数在某一区间上的“整体”性质，因此定义中的x1，x2具有任意性，不能用特殊值来替代；
(3)有些函数在整个定义域内具有单调性，有的函数在定义域内的某个子集上具有单调性。如函数y=3x+5在(-∞,+ ∞)上是单调增函数；函数y=-3x2+1在((-∞,0]上是单调增函数，在[0, +∞)上是单调减函数；函数y= 1/x 在(-∞,0)和(0, +∞)上均为减函数，但不能说成它在定义域(-∞,0) ∪(0, +∞)上是减函数.
证明:
取值
作差变形
定号
判断
题型2 利用定义证明函数的单调性
4.用定义法证明函数单调性的步骤
(1)取值。即设x1，x2是该区间内的任意两个值，且x1(2)求△y。即计算f(x2)-f(x1)，并通过因式分解、配方、有理化等方法，向有利于判断△ y的符号方向变形；
(3)定号。确定△y的符号，当符号不确定时，可以进行分步讨论；
(4)判断。根据定义作出结论。
例4
题型2 利用定义证明函数的单调性
证明：
因为
所以
同理
y=f(x2)－f(x1)< 0
函数的图象如图．
证明:
练习2
证明:函数y=x2-2x-6在(-∞,1]上是减函数;
5.函数单调性的判定方法
(1)定义法。利用定义严格判断；
(2)图象法。作出函数的图象，用数形结合的方法确定函数的单调区间；
(3) 两个函数和（差）的单调性的判断：
增+增=增，减+减=减，增-减=增，减-增=减；
(4) ①f(x)与f(x)+c(c为常数)具有相同的单调性；②当c>0时，函数f(x)与c f(x)具有相同的单调性，当c<0时，函数f(x)与c f(x)具有相反的单调性；③若f(x) ≠0， 则f(x) 与 具有相反的单调性；④若f(x) ≥0， 则f(x) 与 具有相同的单调性。
题型4 函数单调性的应用
例5 定义在[1，5]上的函数f(x)为减函数，求满足不等式f(2a-1)-f(a+1)>0的a的值的集合。
题型4 函数单调性的应用
例6 已知函数f(x)=x2+2(a-3)x+1在区间(-∞,6]上是减函数，求实数a的取值范围。
练习：已知函数f(x)=4x2-mx+1在(-∞,-2]上递减，在(-2,+∞)上递增，求f(1)
(1)
的单调区间_________;
的单调区间_________;
的单调区间_________;
(2)
(3)
练习
(4) 函数y=x2+ax+7在[1, +∞]是增函数,求a的取值范围 .