六年级上册数学课件-5.圆 整理和复习(1) 人教版(19张ppt)
文档属性
| 名称 | 六年级上册数学课件-5.圆 整理和复习(1) 人教版(19张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 8.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-03 17:00:49 | ||
图片预览




文档简介
整理和复习(1)
05
圆
R·六年级上册
本单元你学习了哪些有关圆的知识?
谈话引入,初步回顾
圆心
半径
直径
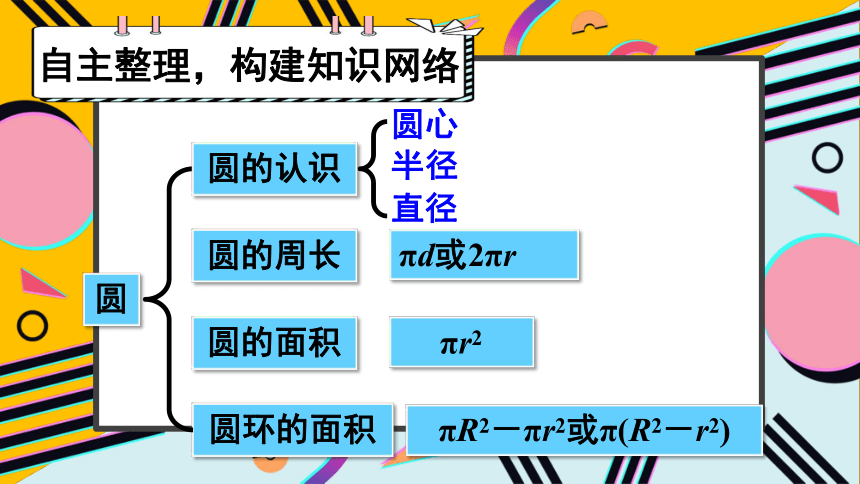
圆环的面积
圆
圆的认识
圆的周长
圆的面积
πd或2πr
πr2
πR2-πr2或π(R2-r2)
自主整理,构建知识网络
r
d
O
S环=πR2-πr2
S环=π×(R2-r2)
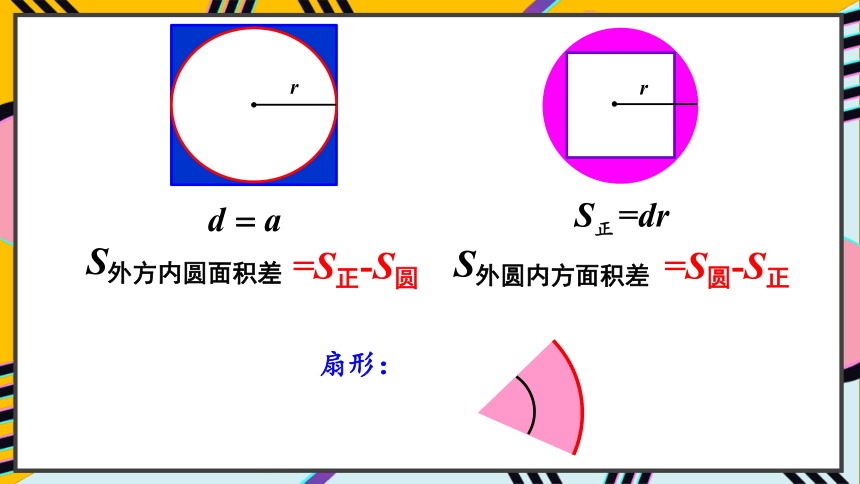
=S正-S圆
S外方内圆面积差
=S圆-S正
S外圆内方面积差
r
r
扇形:
1.请你找出下面圆的圆心。
分别画出正方形的对角线
O
O
[选自教材P77 第1题]
分层练习,巩固提高
O
O
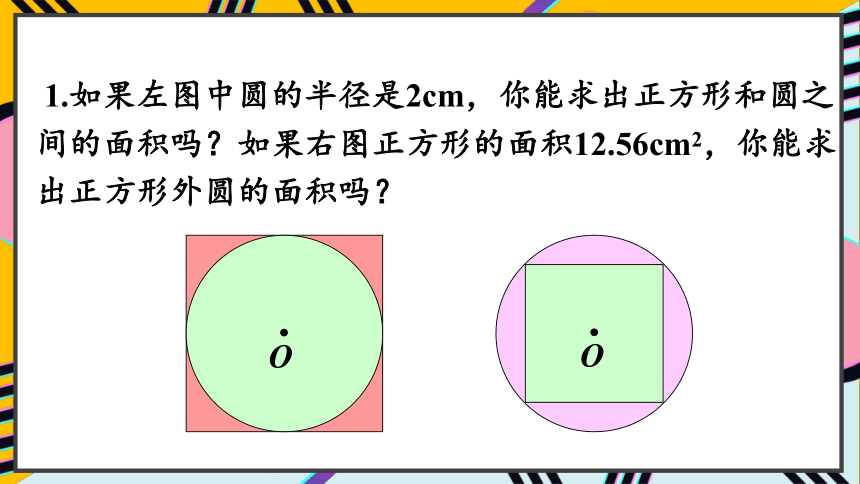
1.如果左图中圆的半径是2cm,你能求出正方形和圆之间的面积吗?如果右图正方形的面积12.56cm2,你能求出正方形外圆的面积吗?
O
(1)如果左图中圆的半径是2cm,你能求出正方形
和圆之间的面积吗?
S=(2+2)2-3.14×22
=16-12.56
=3.44(cm2)
r≈2.51cm
O
(2)如果右图正方形的面积12.56cm2,你能求出正方形外圆的面积吗?
S=3.14×2.512
≈19.78(cm2)
r×d=12.56
2. 一个圆形餐桌面的直径是2m。
(1)它的面积是多少平方米?
(2)如果一个人需要0.5m宽的位置就餐,这张餐桌大约能坐多少人?
3.14×(2÷2)2=3.14(m2)
3.14×2÷0.5=12.56≈12(人)
答:它的面积是3.14 m2 。
答:大约能坐12人。
[选自教材P77 第2题]
2. 一个圆形餐桌面的直径是2m。
(3)如果在这张餐桌的中央放一个半径是0.5m的圆形转盘,剩下的桌面的面积是多少?
2÷2=1(m)
3.14×(12-0.52)
=3.14×(1-0.25)
=3.14×0.75
=2.355(m2)
答:剩下的桌面的面积是2.355m2。
3.判断题。
(1)任何一个圆都有无数条对称轴。 ( )
(2)圆的半径扩大到原来的2倍,周长和面积也扩大到原来的2倍。 ( )
(3)半径相等的两个圆周长相等。 ( )
(4)在两个端点都在圆上的线段中,直径是最长的一条。 ( )
(5)有4个圆心角都是90°的扇形,一定可以拼成一个圆。 ( )
√
×
√
√
×
2.选择正确答案的序号填在括号里。
(1)一个圆的半径是2m,那么它的周长和面积相比,
( )。
A.面积大 B.周长大 C.无法比较
(2)直径是通过圆心并且两端都在圆上的( )。
A.线段 B.直线 C.射线
C
A
(3)把一张圆形纸片沿半径平均分成若干份,
拼成一个近似的长方形,其周长( )。
A.等于圆周长 B.大于圆周长 C.小于圆周长
(4)如图,两个小圆周长之和应( )大圆周长。
A.大于 B.小于 C.等于
(5)用一根同样长的铁丝围成下面的图形,其中面积最大的是( )。
A.长方形 B.正方形 C.圆
B
C
C
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
一、想一想,填一填。
1.用圆规画一个直径为8 cm的圆,圆规的两脚之间的距离应取( ) cm,所画的圆的面积是( ) cm2。
2.大圆半径与小圆半径的比是3:1,大圆直径与小圆直径的比是( ) ,大圆周长是小圆周长的( ) 倍,大圆面积是小圆面积的( )倍。
4
50.24
3∶1
3
9
巩固练习
一、想一想,填一填。
3.一个时钟的分针长6cm,当分针正好转一圈时,它扫过的面积是( )cm2;经过一昼夜,分针的尖端走了( )cm。
113.04
904.32
巩固练习
五、求各图中阴影部分的面积。
4×8=32(cm2)
3.14×(8÷2)2-8×(8÷2)×2
=18.24(cm2)
六、一个圆形桌面,直径是2m。现在在桌面上铺上桌布,桌面周围均匀下垂20 cm,这块桌布的面积是多少平方米?
20cm=0.2m
桌布半径:(2+0.2×2)÷2=1.2(m)
3.14×1.22=4.5216(m2)
答:这块桌布的面积是4.5216平方米。
05
圆
R·六年级上册
本单元你学习了哪些有关圆的知识?
谈话引入,初步回顾
圆心
半径
直径
圆环的面积
圆
圆的认识
圆的周长
圆的面积
πd或2πr
πr2
πR2-πr2或π(R2-r2)
自主整理,构建知识网络
r
d
O
S环=πR2-πr2
S环=π×(R2-r2)
=S正-S圆
S外方内圆面积差
=S圆-S正
S外圆内方面积差
r
r
扇形:
1.请你找出下面圆的圆心。
分别画出正方形的对角线
O
O
[选自教材P77 第1题]
分层练习,巩固提高
O
O
1.如果左图中圆的半径是2cm,你能求出正方形和圆之间的面积吗?如果右图正方形的面积12.56cm2,你能求出正方形外圆的面积吗?
O
(1)如果左图中圆的半径是2cm,你能求出正方形
和圆之间的面积吗?
S=(2+2)2-3.14×22
=16-12.56
=3.44(cm2)
r≈2.51cm
O
(2)如果右图正方形的面积12.56cm2,你能求出正方形外圆的面积吗?
S=3.14×2.512
≈19.78(cm2)
r×d=12.56
2. 一个圆形餐桌面的直径是2m。
(1)它的面积是多少平方米?
(2)如果一个人需要0.5m宽的位置就餐,这张餐桌大约能坐多少人?
3.14×(2÷2)2=3.14(m2)
3.14×2÷0.5=12.56≈12(人)
答:它的面积是3.14 m2 。
答:大约能坐12人。
[选自教材P77 第2题]
2. 一个圆形餐桌面的直径是2m。
(3)如果在这张餐桌的中央放一个半径是0.5m的圆形转盘,剩下的桌面的面积是多少?
2÷2=1(m)
3.14×(12-0.52)
=3.14×(1-0.25)
=3.14×0.75
=2.355(m2)
答:剩下的桌面的面积是2.355m2。
3.判断题。
(1)任何一个圆都有无数条对称轴。 ( )
(2)圆的半径扩大到原来的2倍,周长和面积也扩大到原来的2倍。 ( )
(3)半径相等的两个圆周长相等。 ( )
(4)在两个端点都在圆上的线段中,直径是最长的一条。 ( )
(5)有4个圆心角都是90°的扇形,一定可以拼成一个圆。 ( )
√
×
√
√
×
2.选择正确答案的序号填在括号里。
(1)一个圆的半径是2m,那么它的周长和面积相比,
( )。
A.面积大 B.周长大 C.无法比较
(2)直径是通过圆心并且两端都在圆上的( )。
A.线段 B.直线 C.射线
C
A
(3)把一张圆形纸片沿半径平均分成若干份,
拼成一个近似的长方形,其周长( )。
A.等于圆周长 B.大于圆周长 C.小于圆周长
(4)如图,两个小圆周长之和应( )大圆周长。
A.大于 B.小于 C.等于
(5)用一根同样长的铁丝围成下面的图形,其中面积最大的是( )。
A.长方形 B.正方形 C.圆
B
C
C
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
一、想一想,填一填。
1.用圆规画一个直径为8 cm的圆,圆规的两脚之间的距离应取( ) cm,所画的圆的面积是( ) cm2。
2.大圆半径与小圆半径的比是3:1,大圆直径与小圆直径的比是( ) ,大圆周长是小圆周长的( ) 倍,大圆面积是小圆面积的( )倍。
4
50.24
3∶1
3
9
巩固练习
一、想一想,填一填。
3.一个时钟的分针长6cm,当分针正好转一圈时,它扫过的面积是( )cm2;经过一昼夜,分针的尖端走了( )cm。
113.04
904.32
巩固练习
五、求各图中阴影部分的面积。
4×8=32(cm2)
3.14×(8÷2)2-8×(8÷2)×2
=18.24(cm2)
六、一个圆形桌面,直径是2m。现在在桌面上铺上桌布,桌面周围均匀下垂20 cm,这块桌布的面积是多少平方米?
20cm=0.2m
桌布半径:(2+0.2×2)÷2=1.2(m)
3.14×1.22=4.5216(m2)
答:这块桌布的面积是4.5216平方米。
