沪科版数学七年级下册第10章 相交线、平行线和平移(含答案)
文档属性
| 名称 | 沪科版数学七年级下册第10章 相交线、平行线和平移(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-04 09:27:15 | ||
图片预览

文档简介
沪科版数学七年级下册第10章 相交线、平行线和平移
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列各组图形中可以通过平移其中一个图形得到的是( )
2.下列说法正确的是( )
A.有且只有一条直线垂直于已知直线
B.过一点,有且只有一条直线与已知直线平行
C.在同一平面内,两条直线的位置关系只有两种:相交和垂直
D.如果两条直线都与第三条直线平行,那么这两条直线也互相平行
3.如图,直线AB,CD相交于点O,过点O作OE⊥CD.若∠BOE=32°,则∠AOC的度数为( )
A.32° B.48°
C.58° D.68°
4.如图,下列条件:①∠1=∠2;②∠4=∠5;③∠6+∠4=180°;④∠1=∠3.其中能判断直线l1∥l2的有( )
A.②④ B.③④ C.②③ D.①④
5.如图,一块直角三角尺的一个顶点落在直尺的一边上,若∠2=25°,则∠1的度数为( )
A.75° B.65° C.55° D.45°
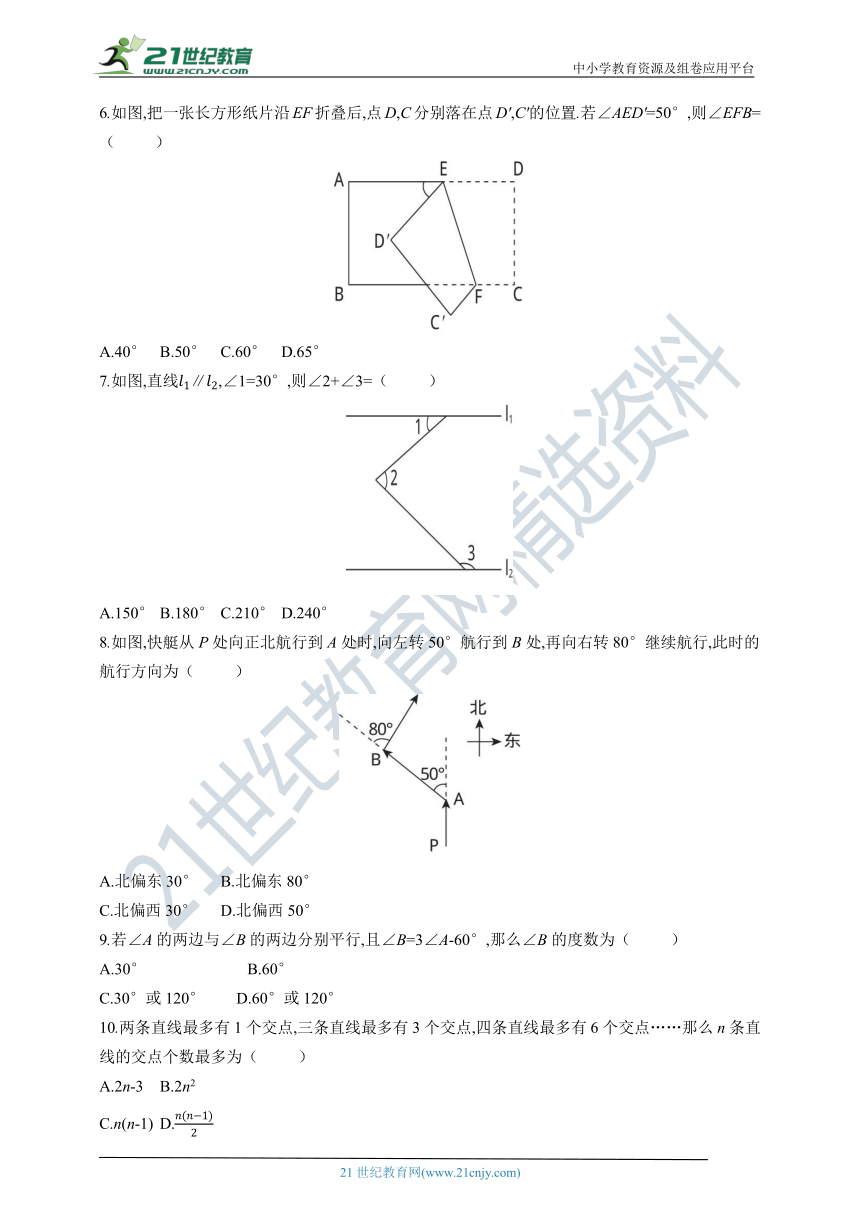
6.如图,把一张长方形纸片沿EF折叠后,点D,C分别落在点D',C'的位置.若∠AED'=50°,则∠EFB=( )
A.40° B.50° C.60° D.65°
7.如图,直线l1∥l2,∠1=30°,则∠2+∠3=( )
A.150° B.180° C.210° D.240°
8.如图,快艇从P处向正北航行到A处时,向左转50°航行到B处,再向右转80°继续航行,此时的航行方向为( )
A.北偏东30° B.北偏东80°
C.北偏西30° D.北偏西50°
9.若∠A的两边与∠B的两边分别平行,且∠B=3∠A-60°,那么∠B的度数为( )
A.30° B.60°
C.30°或120° D.60°或120°
10.两条直线最多有1个交点,三条直线最多有3个交点,四条直线最多有6个交点……那么n条直线的交点个数最多为( )
A.2n-3 B.2n2
C.n(n-1) D.n(n-1)2
二、填空题(本大题共4小题,每小题5分,满分20分)
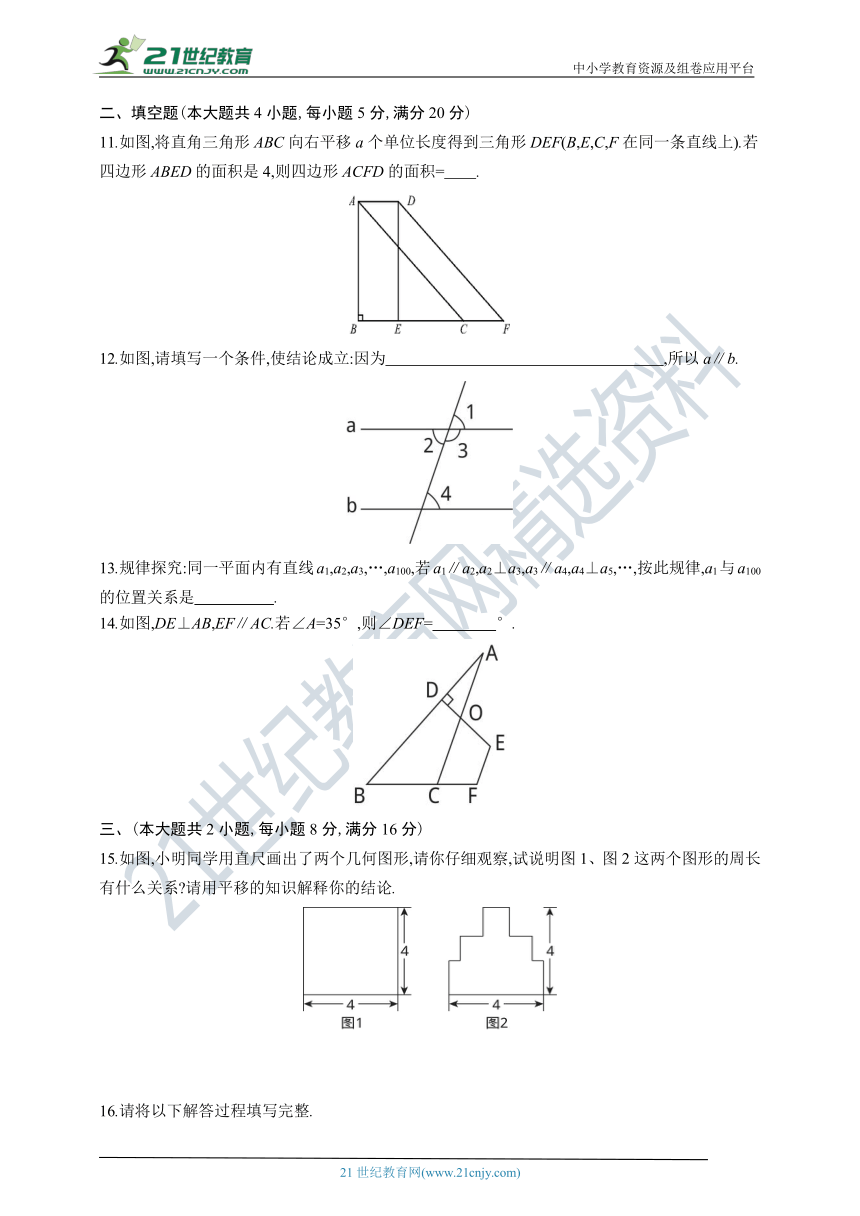
11.如图,将直角三角形ABC向右平移a个单位长度得到三角形DEF(B,E,C,F在同一条直线上).若四边形ABED的面积是4,则四边形ACFD的面积= .?
12.如图,请填写一个条件,使结论成立:因为 ,所以a∥b.?
13.规律探究:同一平面内有直线a1,a2,a3,…,a100,若a1∥a2,a2⊥a3,a3∥a4,a4⊥a5,…,按此规律,a1与a100的位置关系是 .?
14.如图,DE⊥AB,EF∥AC.若∠A=35°,则∠DEF= °.
三、(本大题共2小题,每小题8分,满分16分)
15.如图,小明同学用直尺画出了两个几何图形,请你仔细观察,试说明图1、图2这两个图形的周长有什么关系?请用平移的知识解释你的结论.
16.请将以下解答过程填写完整.
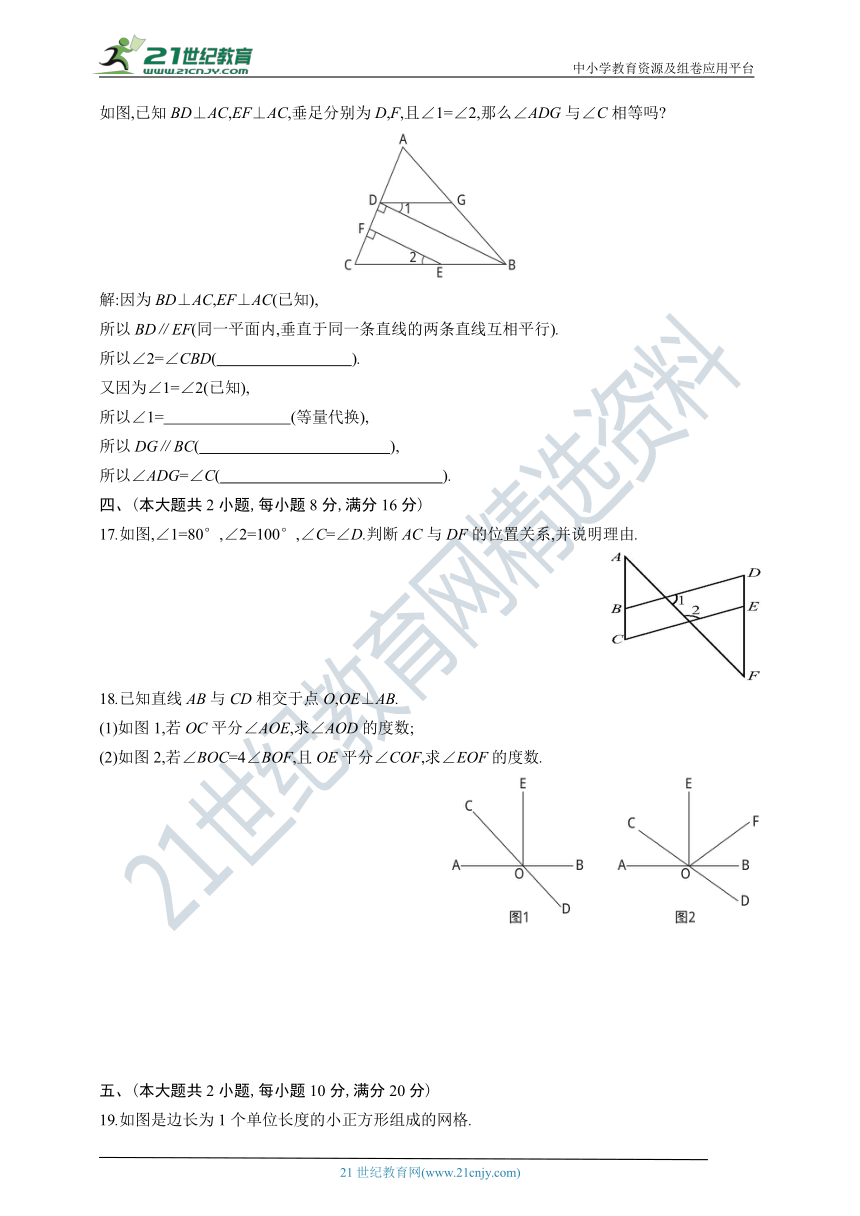
如图,已知BD⊥AC,EF⊥AC,垂足分别为D,F,且∠1=∠2,那么∠ADG与∠C相等吗?
解:因为BD⊥AC,EF⊥AC(已知),
所以BD∥EF(同一平面内,垂直于同一条直线的两条直线互相平行).
所以∠2=∠CBD( ).?
又因为∠1=∠2(已知),
所以∠1= (等量代换),?
所以DG∥BC( ),?
所以∠ADG=∠C( ).?
四、(本大题共2小题,每小题8分,满分16分)
17.如图,∠1=80°,∠2=100°,∠C=∠D.判断AC与DF的位置关系,并说明理由.
18.已知直线AB与CD相交于点O,OE⊥AB.
(1)如图1,若OC平分∠AOE,求∠AOD的度数;
(2)如图2,若∠BOC=4∠BOF,且OE平分∠COF,求∠EOF的度数.
五、(本大题共2小题,每小题10分,满分20分)
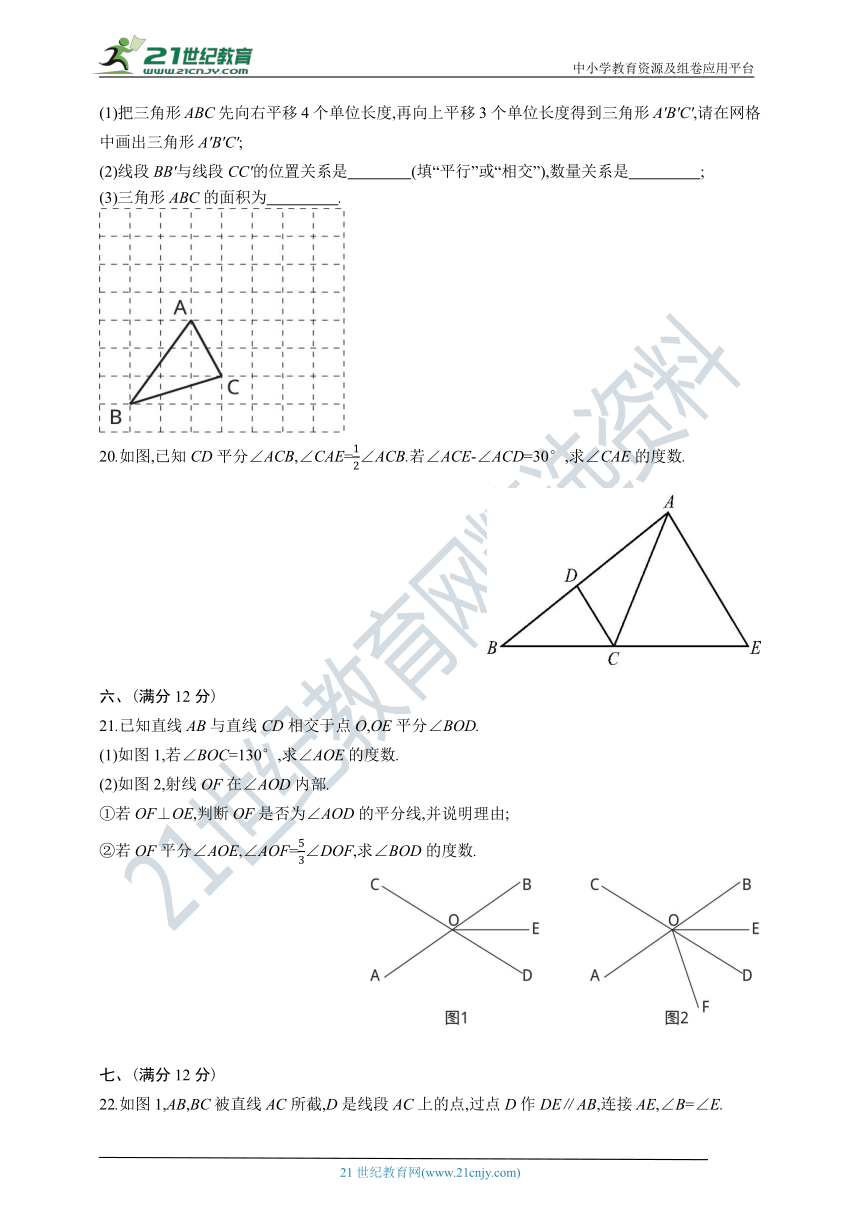
19.如图是边长为1个单位长度的小正方形组成的网格.
(1)把三角形ABC先向右平移4个单位长度,再向上平移3个单位长度得到三角形A'B'C',请在网格中画出三角形A'B'C';
(2)线段BB'与线段CC'的位置关系是 (填“平行”或“相交”),数量关系是 ;?
(3)三角形ABC的面积为? .?
20.如图,已知CD平分∠ACB,∠CAE=12∠ACB.若∠ACE-∠ACD=30°,求∠CAE的度数.
六、(满分12分)
21.已知直线AB与直线CD相交于点O,OE平分∠BOD.
(1)如图1,若∠BOC=130°,求∠AOE的度数.
(2)如图2,射线OF在∠AOD内部.
①若OF⊥OE,判断OF是否为∠AOD的平分线,并说明理由;
②若OF平分∠AOE,∠AOF=53∠DOF,求∠BOD的度数.
七、(满分12分)
22.如图1,AB,BC被直线AC所截,D是线段AC上的点,过点D作DE∥AB,连接AE,∠B=∠E.
(1)试说明:AE∥BC.
(2)如图2,将线段AE沿着直线AC平移得到线段PQ,连接DQ.若∠E=75°,当DE⊥DQ时,求∠Q的度数.
八、(满分14分)
23.如图,l1∥l2,点A在l1上,点B,D在l2上,连接AB,作∠ABD的平分线交l1于点C,设∠ACB=α,E是射线BC上的一个动点.
(1)若AE平分∠BAC,求∠CAE的度数;(用含α的代数式表示)
(2)若点E运动到l1上方,且满足∠BAE=100°,∠BAE∶∠CAE=5∶1,求α的值;
(3)若∠BAE∶∠CAE=n(n>1),求∠CAE的度数.(用含n和α的代数式表示)
附加题
如图1,在平面直角坐标系中,OA=7,OC=18,将点C先向上平移7个单位,再向左平移4个单位,得到点B,连接AB,BC.
(1)填空:点B的坐标为 ;
(2)如图2,BF平分∠ABC交x轴于点F,CD平分∠BCO交BF于点D,过点F作FH⊥BF交BC的延长线于点H,试判断DC与FH的位置关系,并说明理由;
(3)若点P从点C出发以每秒2个单位长度的速度沿CO方向移动,同时点Q从点O出发以每秒1个单位长度的速度沿OA方向移动,设移动的时间为t秒(0<t<7),四边形OPBA与△OQB的面积分别记为S1,S2,是否存在一段时间,使S1<2S2?若存在,求出t的取值范围;若不存在,试说明理由.
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列各组图形中可以通过平移其中一个图形得到的是( B )
2.下列说法正确的是( D )
A.有且只有一条直线垂直于已知直线
B.过一点,有且只有一条直线与已知直线平行
C.在同一平面内,两条直线的位置关系只有两种:相交和垂直
D.如果两条直线都与第三条直线平行,那么这两条直线也互相平行
3.如图,直线AB,CD相交于点O,过点O作OE⊥CD.若∠BOE=32°,则∠AOC的度数为( C )
A.32° B.48°
C.58° D.68°
4.如图,下列条件:①∠1=∠2;②∠4=∠5;③∠6+∠4=180°;④∠1=∠3.其中能判断直线l1∥l2的有( A )
A.②④ B.③④ C.②③ D.①④
5.如图,一块直角三角尺的一个顶点落在直尺的一边上,若∠2=25°,则∠1的度数为( B )
A.75° B.65° C.55° D.45°
6.如图,把一张长方形纸片沿EF折叠后,点D,C分别落在点D',C'的位置.若∠AED'=50°,则∠EFB=( D )
A.40° B.50° C.60° D.65°
7.如图,直线l1∥l2,∠1=30°,则∠2+∠3=( C )
A.150° B.180° C.210° D.240°
8.(铜陵期末)如图,快艇从P处向正北航行到A处时,向左转50°航行到B处,再向右转80°继续航行,此时的航行方向为( A )
A.北偏东30° B.北偏东80°
C.北偏西30° D.北偏西50°
9.若∠A的两边与∠B的两边分别平行,且∠B=3∠A-60°,那么∠B的度数为( C )
A.30° B.60°
C.30°或120° D.60°或120°
【解析】因为∠A与∠B的两边分别平行,所以∠A=∠B或∠A+∠B=180°.当∠A=∠B时,因为∠B=3∠A-60°,所以∠B=3∠B-60°,解得∠B=30°;当∠A+∠B=180°时,因为∠B=3∠A-60°,所以∠B=3(180°-∠B)-60°,解得∠B=120°.综上所述,∠B=30°或120°.
10.两条直线最多有1个交点,三条直线最多有3个交点,四条直线最多有6个交点……那么n条直线的交点个数最多为( D )
A.2n-3 B.2n2
C.n(n-1) D.n(n-1)2
【解析】因为两条直线相交,最多有1个交点;三条直线相交,最多有1+2=3个交点;四条直线相交,最多有1+2+3=6个交点……所以n条直线相交,最多有1+2+3+…+(n-1)=n(n-1)2个交点.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,将直角三角形ABC向右平移a个单位长度得到三角形DEF(B,E,C,F在同一条直线上).若四边形ABED的面积是4,则四边形ACFD的面积= 4 .?
12.如图,请填写一个条件,使结论成立:因为 ∠1=∠4(或∠2=∠4或∠3+∠4=180°) ,所以a∥b.?
13.(蚌埠期末)规律探究:同一平面内有直线a1,a2,a3,…,a100,若a1∥a2,a2⊥a3,a3∥a4,a4⊥a5,…,按此规律,a1与a100的位置关系是 a1⊥a100 .?
【解析】因为a1∥a2,a2⊥a3,a3∥a4,所以a1⊥a4,按此规律,可得a5⊥a8,又因为a4⊥a5,…,所以a1⊥a8,由此类推,a1⊥a4n,所以a1⊥a100.
14.如图,DE⊥AB,EF∥AC.若∠A=35°,则∠DEF= 125 °.
【解析】因为DE⊥AB,所以∠ADO=90°.因为∠A=35°,所以∠DOA=90°-35°=55°,所以∠COE=∠DOA=55°.因为EF∥AC,所以∠DEF=180°-∠COE=180°-55°=125°.
三、(本大题共2小题,每小题8分,满分16分)
15.如图,小明同学用直尺画出了两个几何图形,请你仔细观察,试说明图1、图2这两个图形的周长有什么关系?请用平移的知识解释你的结论.
解:图1、图2的周长相等.
理由:图1是边长为4的正方形,将图2的横、纵线段分别平移,即可得出边长正好为4的正方形,所以图1、图2的周长相等.
16.请将以下解答过程填写完整.
如图,已知BD⊥AC,EF⊥AC,垂足分别为D,F,且∠1=∠2,那么∠ADG与∠C相等吗?
解:因为BD⊥AC,EF⊥AC(已知),
所以BD∥EF(同一平面内,垂直于同一条直线的两条直线互相平行).
所以∠2=∠CBD( 两直线平行,同位角相等 ).?
又因为∠1=∠2(已知),
所以∠1= ∠CBD (等量代换),?
所以DG∥BC( 内错角相等,两直线平行 ),?
所以∠ADG=∠C( 两直线平行,同位角相等 ).?
四、(本大题共2小题,每小题8分,满分16分)
17.如图,∠1=80°,∠2=100°,∠C=∠D.判断AC与DF的位置关系,并说明理由.
解:AC∥DF.
理由:因为∠1=80°,∠2=100°,
所以∠1+∠2=180°,
所以BD∥CE,所以∠C=∠ABD.
因为∠C=∠D,所以∠ABD=∠D,
所以AC∥DF.
18.已知直线AB与CD相交于点O,OE⊥AB.
(1)如图1,若OC平分∠AOE,求∠AOD的度数;
(2)如图2,若∠BOC=4∠BOF,且OE平分∠COF,求∠EOF的度数.
解:(1)因为∠AOE=90°,OC平分∠AOE,
所以∠AOC=45°,
所以∠AOD=180°-∠AOC=135°.
(2)因为OE⊥AB,所以∠AOE=∠BOE=90°.
因为OE平分∠COF,所以∠EOF=∠COE,
所以∠BOE-∠EOF=∠AOE-∠COE,
即∠BOF=∠AOC.
因为∠BOC=4∠BOF,所以∠BOC=4∠AOC.
又因为∠BOC+∠AOC=180°,
即4∠AOC+∠AOC=180°,解得∠AOC=36°,
所以∠BOF=∠AOC=36°,
所以∠EOF=∠BOE-∠BOF=90°-36°=54°.
五、(本大题共2小题,每小题10分,满分20分)
19.如图是边长为1个单位长度的小正方形组成的网格.
(1)把三角形ABC先向右平移4个单位长度,再向上平移3个单位长度得到三角形A'B'C',请在网格中画出三角形A'B'C';
(2)线段BB'与线段CC'的位置关系是 平行 (填“平行”或“相交”),数量关系是 相等 ;?
(3)三角形ABC的面积为?72 .?
解:(1)图略.
20.如图,已知CD平分∠ACB,∠CAE=12∠ACB.若∠ACE-∠ACD=30°,求∠CAE的度数.
解:因为CD平分∠ACB,所以∠ACD=12∠ACB,
所以∠ACE+2∠ACD=180°. ①
又因为∠ACE-∠ACD=30°, ②
所以联立①②,解得∠ACD=50°.
因为∠CAE=12∠ACB,所以∠CAE=∠ACD=50°.
六、(满分12分)
21.已知直线AB与直线CD相交于点O,OE平分∠BOD.
(1)如图1,若∠BOC=130°,求∠AOE的度数.
(2)如图2,射线OF在∠AOD内部.
①若OF⊥OE,判断OF是否为∠AOD的平分线,并说明理由;
②若OF平分∠AOE,∠AOF=53∠DOF,求∠BOD的度数.
解:(1)因为∠BOC=130°,所以∠AOD=∠BOC=130°,∠BOD=180°-∠BOC=50°.
因为OE平分∠BOD,所以∠DOE=25°,
所以∠AOE=∠AOD+∠DOE=155°.
(2)①OF是∠AOD的平分线.
理由:因为OF⊥OE,所以∠EOF=90°,
所以∠BOE+∠AOF=90°.
因为OE平分∠BOD,所以∠BOE=∠DOE,
所以∠DOE+∠AOF=90°,
又因为∠DOE+∠DOF=90°,所以∠AOF=∠DOF,
所以OF是∠AOD的平分线.
②因为∠AOF=53∠DOF,
可设∠DOF=3x,则∠AOF=∠5x.
因为OF平分∠AOE,所以∠AOF=∠EOF=5x,
所以∠DOE=∠EOF-∠DOF=2x.
因为OE平分∠BOD,所以∠BOD=2∠DOE=4x,
所以5x+3x+4x=180°,解得x=15°,
所以∠BOD=4x=60°.
七、(满分12分)
22.如图1,AB,BC被直线AC所截,D是线段AC上的点,过点D作DE∥AB,连接AE,∠B=∠E.
(1)试说明:AE∥BC.
(2)如图2,将线段AE沿着直线AC平移得到线段PQ,连接DQ.若∠E=75°,当DE⊥DQ时,求∠Q的度数.
解:(1)因为DE∥AB,所以∠BAE+∠E=180°.
因为∠B=∠E,所以∠BAE+∠B=180°,
所以AE∥BC.
(2)过点D作DF∥AE(点F在点D右侧),
所以∠EDF=∠E=75°.
因为PQ∥AE,所以DF∥PQ,
所以∠FDQ=∠Q.
因为DE⊥DQ,所以∠EDQ=90°,
所以∠Q=∠FDQ=90°-75°=15°.
八、(满分14分)
23.如图,l1∥l2,点A在l1上,点B,D在l2上,连接AB,作∠ABD的平分线交l1于点C,设∠ACB=α,E是射线BC上的一个动点.
(1)若AE平分∠BAC,求∠CAE的度数;(用含α的代数式表示)
(2)若点E运动到l1上方,且满足∠BAE=100°,∠BAE∶∠CAE=5∶1,求α的值;
(3)若∠BAE∶∠CAE=n(n>1),求∠CAE的度数.(用含n和α的代数式表示)
解:(1)因为∠ACB=α,l1∥l2,所以∠CBD=∠ACB=α.
因为BC平分∠ABD,所以∠ABC=∠CBD=α,
所以∠CAB=180°-∠ABC-∠ACB=180°-2α.
又因为AE平分∠CAB,所以∠CAE=12∠CAB=90°-α.
(2)如图1.因为∠BAE=100°,∠BAE∶∠CAE=5∶1,
所以∠CAE=20°,所以∠BAC=∠BAE-∠CAE=80°.
因为AC∥BD,
所以∠ABD=180°-∠BAC=100°,∠ACB=∠CBD.
因为BC平分∠ABD,所以∠CBD=12∠ABD=50°,
所以α=∠CBD=50°.
(3)①如图2.因为AC∥BD,所以∠CBD=∠ACB=α.
因为BC平分∠ABD,所以∠ABD=2∠CBD=2α,
所以∠BAC=180°-∠ABD=180°-2α.
因为∠BAE∶∠CAE=n,
所以(∠BAC+∠CAE)∶∠CAE=n,解得∠CAE=180°-2αn-1.
②如图3.由①知∠BAC=180°-2α.
因为∠BAE∶∠CAE=n,
所以(∠BAC-∠CAE)∶∠CAE=n,解得∠CAE=180°-2αn+1.
综上所述,∠CAE的度数为180°-2αn-1或180°-2αn+1.
附加题
如图1,在平面直角坐标系中,OA=7,OC=18,将点C先向上平移7个单位,再向左平移4个单位,得到点B,连接AB,BC.
(1)填空:点B的坐标为 ;
(2)如图2,BF平分∠ABC交x轴于点F,CD平分∠BCO交BF于点D,过点F作FH⊥BF交BC的延长线于点H,试判断DC与FH的位置关系,并说明理由;
(3)若点P从点C出发以每秒2个单位长度的速度沿CO方向移动,同时点Q从点O出发以每秒1个单位长度的速度沿OA方向移动,设移动的时间为t秒(0<t<7),四边形OPBA与△OQB的面积分别记为S1,S2,是否存在一段时间,使S1<2S2?若存在,求出t的取值范围;若不存在,试说明理由.
解: (1) 将点C先向上平移7个单位,即点C落在AB的延长线上,纵坐标为7,横坐标为18,再向左平移4个单位,横坐标变为18-4=14,故其坐标为(14,7);
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列各组图形中可以通过平移其中一个图形得到的是( )
2.下列说法正确的是( )
A.有且只有一条直线垂直于已知直线
B.过一点,有且只有一条直线与已知直线平行
C.在同一平面内,两条直线的位置关系只有两种:相交和垂直
D.如果两条直线都与第三条直线平行,那么这两条直线也互相平行
3.如图,直线AB,CD相交于点O,过点O作OE⊥CD.若∠BOE=32°,则∠AOC的度数为( )
A.32° B.48°
C.58° D.68°
4.如图,下列条件:①∠1=∠2;②∠4=∠5;③∠6+∠4=180°;④∠1=∠3.其中能判断直线l1∥l2的有( )
A.②④ B.③④ C.②③ D.①④
5.如图,一块直角三角尺的一个顶点落在直尺的一边上,若∠2=25°,则∠1的度数为( )
A.75° B.65° C.55° D.45°
6.如图,把一张长方形纸片沿EF折叠后,点D,C分别落在点D',C'的位置.若∠AED'=50°,则∠EFB=( )
A.40° B.50° C.60° D.65°
7.如图,直线l1∥l2,∠1=30°,则∠2+∠3=( )
A.150° B.180° C.210° D.240°
8.如图,快艇从P处向正北航行到A处时,向左转50°航行到B处,再向右转80°继续航行,此时的航行方向为( )
A.北偏东30° B.北偏东80°
C.北偏西30° D.北偏西50°
9.若∠A的两边与∠B的两边分别平行,且∠B=3∠A-60°,那么∠B的度数为( )
A.30° B.60°
C.30°或120° D.60°或120°
10.两条直线最多有1个交点,三条直线最多有3个交点,四条直线最多有6个交点……那么n条直线的交点个数最多为( )
A.2n-3 B.2n2
C.n(n-1) D.n(n-1)2
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,将直角三角形ABC向右平移a个单位长度得到三角形DEF(B,E,C,F在同一条直线上).若四边形ABED的面积是4,则四边形ACFD的面积= .?
12.如图,请填写一个条件,使结论成立:因为 ,所以a∥b.?
13.规律探究:同一平面内有直线a1,a2,a3,…,a100,若a1∥a2,a2⊥a3,a3∥a4,a4⊥a5,…,按此规律,a1与a100的位置关系是 .?
14.如图,DE⊥AB,EF∥AC.若∠A=35°,则∠DEF= °.
三、(本大题共2小题,每小题8分,满分16分)
15.如图,小明同学用直尺画出了两个几何图形,请你仔细观察,试说明图1、图2这两个图形的周长有什么关系?请用平移的知识解释你的结论.
16.请将以下解答过程填写完整.
如图,已知BD⊥AC,EF⊥AC,垂足分别为D,F,且∠1=∠2,那么∠ADG与∠C相等吗?
解:因为BD⊥AC,EF⊥AC(已知),
所以BD∥EF(同一平面内,垂直于同一条直线的两条直线互相平行).
所以∠2=∠CBD( ).?
又因为∠1=∠2(已知),
所以∠1= (等量代换),?
所以DG∥BC( ),?
所以∠ADG=∠C( ).?
四、(本大题共2小题,每小题8分,满分16分)
17.如图,∠1=80°,∠2=100°,∠C=∠D.判断AC与DF的位置关系,并说明理由.
18.已知直线AB与CD相交于点O,OE⊥AB.
(1)如图1,若OC平分∠AOE,求∠AOD的度数;
(2)如图2,若∠BOC=4∠BOF,且OE平分∠COF,求∠EOF的度数.
五、(本大题共2小题,每小题10分,满分20分)
19.如图是边长为1个单位长度的小正方形组成的网格.
(1)把三角形ABC先向右平移4个单位长度,再向上平移3个单位长度得到三角形A'B'C',请在网格中画出三角形A'B'C';
(2)线段BB'与线段CC'的位置关系是 (填“平行”或“相交”),数量关系是 ;?
(3)三角形ABC的面积为? .?
20.如图,已知CD平分∠ACB,∠CAE=12∠ACB.若∠ACE-∠ACD=30°,求∠CAE的度数.
六、(满分12分)
21.已知直线AB与直线CD相交于点O,OE平分∠BOD.
(1)如图1,若∠BOC=130°,求∠AOE的度数.
(2)如图2,射线OF在∠AOD内部.
①若OF⊥OE,判断OF是否为∠AOD的平分线,并说明理由;
②若OF平分∠AOE,∠AOF=53∠DOF,求∠BOD的度数.
七、(满分12分)
22.如图1,AB,BC被直线AC所截,D是线段AC上的点,过点D作DE∥AB,连接AE,∠B=∠E.
(1)试说明:AE∥BC.
(2)如图2,将线段AE沿着直线AC平移得到线段PQ,连接DQ.若∠E=75°,当DE⊥DQ时,求∠Q的度数.
八、(满分14分)
23.如图,l1∥l2,点A在l1上,点B,D在l2上,连接AB,作∠ABD的平分线交l1于点C,设∠ACB=α,E是射线BC上的一个动点.
(1)若AE平分∠BAC,求∠CAE的度数;(用含α的代数式表示)
(2)若点E运动到l1上方,且满足∠BAE=100°,∠BAE∶∠CAE=5∶1,求α的值;
(3)若∠BAE∶∠CAE=n(n>1),求∠CAE的度数.(用含n和α的代数式表示)
附加题
如图1,在平面直角坐标系中,OA=7,OC=18,将点C先向上平移7个单位,再向左平移4个单位,得到点B,连接AB,BC.
(1)填空:点B的坐标为 ;
(2)如图2,BF平分∠ABC交x轴于点F,CD平分∠BCO交BF于点D,过点F作FH⊥BF交BC的延长线于点H,试判断DC与FH的位置关系,并说明理由;
(3)若点P从点C出发以每秒2个单位长度的速度沿CO方向移动,同时点Q从点O出发以每秒1个单位长度的速度沿OA方向移动,设移动的时间为t秒(0<t<7),四边形OPBA与△OQB的面积分别记为S1,S2,是否存在一段时间,使S1<2S2?若存在,求出t的取值范围;若不存在,试说明理由.
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列各组图形中可以通过平移其中一个图形得到的是( B )
2.下列说法正确的是( D )
A.有且只有一条直线垂直于已知直线
B.过一点,有且只有一条直线与已知直线平行
C.在同一平面内,两条直线的位置关系只有两种:相交和垂直
D.如果两条直线都与第三条直线平行,那么这两条直线也互相平行
3.如图,直线AB,CD相交于点O,过点O作OE⊥CD.若∠BOE=32°,则∠AOC的度数为( C )
A.32° B.48°
C.58° D.68°
4.如图,下列条件:①∠1=∠2;②∠4=∠5;③∠6+∠4=180°;④∠1=∠3.其中能判断直线l1∥l2的有( A )
A.②④ B.③④ C.②③ D.①④
5.如图,一块直角三角尺的一个顶点落在直尺的一边上,若∠2=25°,则∠1的度数为( B )
A.75° B.65° C.55° D.45°
6.如图,把一张长方形纸片沿EF折叠后,点D,C分别落在点D',C'的位置.若∠AED'=50°,则∠EFB=( D )
A.40° B.50° C.60° D.65°
7.如图,直线l1∥l2,∠1=30°,则∠2+∠3=( C )
A.150° B.180° C.210° D.240°
8.(铜陵期末)如图,快艇从P处向正北航行到A处时,向左转50°航行到B处,再向右转80°继续航行,此时的航行方向为( A )
A.北偏东30° B.北偏东80°
C.北偏西30° D.北偏西50°
9.若∠A的两边与∠B的两边分别平行,且∠B=3∠A-60°,那么∠B的度数为( C )
A.30° B.60°
C.30°或120° D.60°或120°
【解析】因为∠A与∠B的两边分别平行,所以∠A=∠B或∠A+∠B=180°.当∠A=∠B时,因为∠B=3∠A-60°,所以∠B=3∠B-60°,解得∠B=30°;当∠A+∠B=180°时,因为∠B=3∠A-60°,所以∠B=3(180°-∠B)-60°,解得∠B=120°.综上所述,∠B=30°或120°.
10.两条直线最多有1个交点,三条直线最多有3个交点,四条直线最多有6个交点……那么n条直线的交点个数最多为( D )
A.2n-3 B.2n2
C.n(n-1) D.n(n-1)2
【解析】因为两条直线相交,最多有1个交点;三条直线相交,最多有1+2=3个交点;四条直线相交,最多有1+2+3=6个交点……所以n条直线相交,最多有1+2+3+…+(n-1)=n(n-1)2个交点.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,将直角三角形ABC向右平移a个单位长度得到三角形DEF(B,E,C,F在同一条直线上).若四边形ABED的面积是4,则四边形ACFD的面积= 4 .?
12.如图,请填写一个条件,使结论成立:因为 ∠1=∠4(或∠2=∠4或∠3+∠4=180°) ,所以a∥b.?
13.(蚌埠期末)规律探究:同一平面内有直线a1,a2,a3,…,a100,若a1∥a2,a2⊥a3,a3∥a4,a4⊥a5,…,按此规律,a1与a100的位置关系是 a1⊥a100 .?
【解析】因为a1∥a2,a2⊥a3,a3∥a4,所以a1⊥a4,按此规律,可得a5⊥a8,又因为a4⊥a5,…,所以a1⊥a8,由此类推,a1⊥a4n,所以a1⊥a100.
14.如图,DE⊥AB,EF∥AC.若∠A=35°,则∠DEF= 125 °.
【解析】因为DE⊥AB,所以∠ADO=90°.因为∠A=35°,所以∠DOA=90°-35°=55°,所以∠COE=∠DOA=55°.因为EF∥AC,所以∠DEF=180°-∠COE=180°-55°=125°.
三、(本大题共2小题,每小题8分,满分16分)
15.如图,小明同学用直尺画出了两个几何图形,请你仔细观察,试说明图1、图2这两个图形的周长有什么关系?请用平移的知识解释你的结论.
解:图1、图2的周长相等.
理由:图1是边长为4的正方形,将图2的横、纵线段分别平移,即可得出边长正好为4的正方形,所以图1、图2的周长相等.
16.请将以下解答过程填写完整.
如图,已知BD⊥AC,EF⊥AC,垂足分别为D,F,且∠1=∠2,那么∠ADG与∠C相等吗?
解:因为BD⊥AC,EF⊥AC(已知),
所以BD∥EF(同一平面内,垂直于同一条直线的两条直线互相平行).
所以∠2=∠CBD( 两直线平行,同位角相等 ).?
又因为∠1=∠2(已知),
所以∠1= ∠CBD (等量代换),?
所以DG∥BC( 内错角相等,两直线平行 ),?
所以∠ADG=∠C( 两直线平行,同位角相等 ).?
四、(本大题共2小题,每小题8分,满分16分)
17.如图,∠1=80°,∠2=100°,∠C=∠D.判断AC与DF的位置关系,并说明理由.
解:AC∥DF.
理由:因为∠1=80°,∠2=100°,
所以∠1+∠2=180°,
所以BD∥CE,所以∠C=∠ABD.
因为∠C=∠D,所以∠ABD=∠D,
所以AC∥DF.
18.已知直线AB与CD相交于点O,OE⊥AB.
(1)如图1,若OC平分∠AOE,求∠AOD的度数;
(2)如图2,若∠BOC=4∠BOF,且OE平分∠COF,求∠EOF的度数.
解:(1)因为∠AOE=90°,OC平分∠AOE,
所以∠AOC=45°,
所以∠AOD=180°-∠AOC=135°.
(2)因为OE⊥AB,所以∠AOE=∠BOE=90°.
因为OE平分∠COF,所以∠EOF=∠COE,
所以∠BOE-∠EOF=∠AOE-∠COE,
即∠BOF=∠AOC.
因为∠BOC=4∠BOF,所以∠BOC=4∠AOC.
又因为∠BOC+∠AOC=180°,
即4∠AOC+∠AOC=180°,解得∠AOC=36°,
所以∠BOF=∠AOC=36°,
所以∠EOF=∠BOE-∠BOF=90°-36°=54°.
五、(本大题共2小题,每小题10分,满分20分)
19.如图是边长为1个单位长度的小正方形组成的网格.
(1)把三角形ABC先向右平移4个单位长度,再向上平移3个单位长度得到三角形A'B'C',请在网格中画出三角形A'B'C';
(2)线段BB'与线段CC'的位置关系是 平行 (填“平行”或“相交”),数量关系是 相等 ;?
(3)三角形ABC的面积为?72 .?
解:(1)图略.
20.如图,已知CD平分∠ACB,∠CAE=12∠ACB.若∠ACE-∠ACD=30°,求∠CAE的度数.
解:因为CD平分∠ACB,所以∠ACD=12∠ACB,
所以∠ACE+2∠ACD=180°. ①
又因为∠ACE-∠ACD=30°, ②
所以联立①②,解得∠ACD=50°.
因为∠CAE=12∠ACB,所以∠CAE=∠ACD=50°.
六、(满分12分)
21.已知直线AB与直线CD相交于点O,OE平分∠BOD.
(1)如图1,若∠BOC=130°,求∠AOE的度数.
(2)如图2,射线OF在∠AOD内部.
①若OF⊥OE,判断OF是否为∠AOD的平分线,并说明理由;
②若OF平分∠AOE,∠AOF=53∠DOF,求∠BOD的度数.
解:(1)因为∠BOC=130°,所以∠AOD=∠BOC=130°,∠BOD=180°-∠BOC=50°.
因为OE平分∠BOD,所以∠DOE=25°,
所以∠AOE=∠AOD+∠DOE=155°.
(2)①OF是∠AOD的平分线.
理由:因为OF⊥OE,所以∠EOF=90°,
所以∠BOE+∠AOF=90°.
因为OE平分∠BOD,所以∠BOE=∠DOE,
所以∠DOE+∠AOF=90°,
又因为∠DOE+∠DOF=90°,所以∠AOF=∠DOF,
所以OF是∠AOD的平分线.
②因为∠AOF=53∠DOF,
可设∠DOF=3x,则∠AOF=∠5x.
因为OF平分∠AOE,所以∠AOF=∠EOF=5x,
所以∠DOE=∠EOF-∠DOF=2x.
因为OE平分∠BOD,所以∠BOD=2∠DOE=4x,
所以5x+3x+4x=180°,解得x=15°,
所以∠BOD=4x=60°.
七、(满分12分)
22.如图1,AB,BC被直线AC所截,D是线段AC上的点,过点D作DE∥AB,连接AE,∠B=∠E.
(1)试说明:AE∥BC.
(2)如图2,将线段AE沿着直线AC平移得到线段PQ,连接DQ.若∠E=75°,当DE⊥DQ时,求∠Q的度数.
解:(1)因为DE∥AB,所以∠BAE+∠E=180°.
因为∠B=∠E,所以∠BAE+∠B=180°,
所以AE∥BC.
(2)过点D作DF∥AE(点F在点D右侧),
所以∠EDF=∠E=75°.
因为PQ∥AE,所以DF∥PQ,
所以∠FDQ=∠Q.
因为DE⊥DQ,所以∠EDQ=90°,
所以∠Q=∠FDQ=90°-75°=15°.
八、(满分14分)
23.如图,l1∥l2,点A在l1上,点B,D在l2上,连接AB,作∠ABD的平分线交l1于点C,设∠ACB=α,E是射线BC上的一个动点.
(1)若AE平分∠BAC,求∠CAE的度数;(用含α的代数式表示)
(2)若点E运动到l1上方,且满足∠BAE=100°,∠BAE∶∠CAE=5∶1,求α的值;
(3)若∠BAE∶∠CAE=n(n>1),求∠CAE的度数.(用含n和α的代数式表示)
解:(1)因为∠ACB=α,l1∥l2,所以∠CBD=∠ACB=α.
因为BC平分∠ABD,所以∠ABC=∠CBD=α,
所以∠CAB=180°-∠ABC-∠ACB=180°-2α.
又因为AE平分∠CAB,所以∠CAE=12∠CAB=90°-α.
(2)如图1.因为∠BAE=100°,∠BAE∶∠CAE=5∶1,
所以∠CAE=20°,所以∠BAC=∠BAE-∠CAE=80°.
因为AC∥BD,
所以∠ABD=180°-∠BAC=100°,∠ACB=∠CBD.
因为BC平分∠ABD,所以∠CBD=12∠ABD=50°,
所以α=∠CBD=50°.
(3)①如图2.因为AC∥BD,所以∠CBD=∠ACB=α.
因为BC平分∠ABD,所以∠ABD=2∠CBD=2α,
所以∠BAC=180°-∠ABD=180°-2α.
因为∠BAE∶∠CAE=n,
所以(∠BAC+∠CAE)∶∠CAE=n,解得∠CAE=180°-2αn-1.
②如图3.由①知∠BAC=180°-2α.
因为∠BAE∶∠CAE=n,
所以(∠BAC-∠CAE)∶∠CAE=n,解得∠CAE=180°-2αn+1.
综上所述,∠CAE的度数为180°-2αn-1或180°-2αn+1.
附加题
如图1,在平面直角坐标系中,OA=7,OC=18,将点C先向上平移7个单位,再向左平移4个单位,得到点B,连接AB,BC.
(1)填空:点B的坐标为 ;
(2)如图2,BF平分∠ABC交x轴于点F,CD平分∠BCO交BF于点D,过点F作FH⊥BF交BC的延长线于点H,试判断DC与FH的位置关系,并说明理由;
(3)若点P从点C出发以每秒2个单位长度的速度沿CO方向移动,同时点Q从点O出发以每秒1个单位长度的速度沿OA方向移动,设移动的时间为t秒(0<t<7),四边形OPBA与△OQB的面积分别记为S1,S2,是否存在一段时间,使S1<2S2?若存在,求出t的取值范围;若不存在,试说明理由.
解: (1) 将点C先向上平移7个单位,即点C落在AB的延长线上,纵坐标为7,横坐标为18,再向左平移4个单位,横坐标变为18-4=14,故其坐标为(14,7);
