人教版数学九年级上册 24.1.4 圆周角 教案
文档属性
| 名称 | 人教版数学九年级上册 24.1.4 圆周角 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 201.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-06 00:00:00 | ||
图片预览


文档简介
24.1.4
圆周角
第1课时
圆周角定理及推论
一、教学目标
1.理解圆周角的概念,识别圆心角和圆周角.
2.理解圆周角定理及其推论.
3.熟练掌握圆周角定理及其推论的灵活运用.
二、教学重难点
重点
掌握圆周角定理和推论及运用.
难点
运用分类思想证明圆周角定理.
重难点解读
1.圆周角定理及其推论1成立的前提是在同圆或等圆中.
2.在同圆或等圆中,如果两个圆周角相等,那么它们所对的弧相等,所对的弦也相等.
3.由圆周角定理推论2可知,如果一个三角形一条边上的中线等于这条边的一半,那么这个三角形是以这条边为斜边的直角三角形.
4.求一条弦所对的圆周角的度数时,应注意这条弦所对的圆周角有两种情况.
5.在同圆或等圆中,一条弦两侧所对的两个圆周角的度数之和是180°.
6.圆心角与圆周角是圆内经常出现的两种角,巧用“一条弧所对的圆周角是它所对的圆心角的一半”这一结论,可以帮助我们实现圆周角与圆心角之间的转化.
三、教学过程
活动1
旧知回顾
1.什么叫圆心角?
2.圆心角、弦、弧之间有什么内在联系?
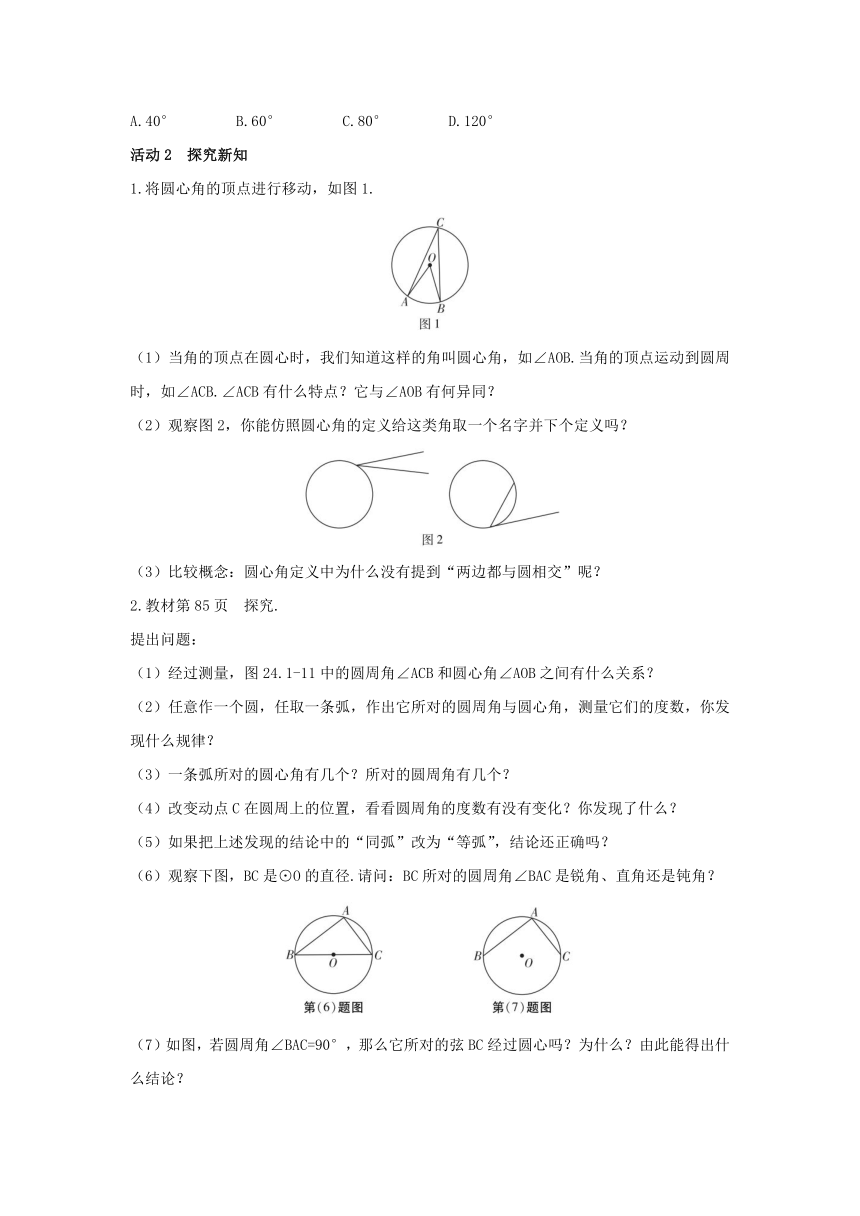
3.如图,已知AB是⊙O的直径,C,D是的三等分点,∠AOE=60°,则∠COE的大小是(
)
A.40°
B.60°
C.80°
D.120°
活动2
探究新知
1.将圆心角的顶点进行移动,如图1.
(1)当角的顶点在圆心时,我们知道这样的角叫圆心角,如∠AOB.当角的顶点运动到圆周时,如∠ACB.∠ACB有什么特点?它与∠AOB有何异同?
(2)观察图2,你能仿照圆心角的定义给这类角取一个名字并下个定义吗?
(3)比较概念:圆心角定义中为什么没有提到“两边都与圆相交”呢?
2.教材第85页
探究.
提出问题:
(1)经过测量,图24.1-11中的圆周角∠ACB和圆心角∠AOB之间有什么关系?
(2)任意作一个圆,任取一条弧,作出它所对的圆周角与圆心角,测量它们的度数,你发现什么规律?
(3)一条弧所对的圆心角有几个?所对的圆周角有几个?
(4)改变动点C在圆周上的位置,看看圆周角的度数有没有变化?你发现了什么?
(5)如果把上述发现的结论中的“同弧”改为“等弧”,结论还正确吗?
(6)观察下图,BC是⊙O的直径.请问:BC所对的圆周角∠BAC是锐角、直角还是钝角?
(7)如图,若圆周角∠BAC=90°,那么它所对的弦BC经过圆心吗?为什么?由此能得出什么结论?
活动3
知识归纳
1.顶点在圆上,并且两边都与圆相交的角叫做圆周角.
2.圆周角定理:一条弧所对的圆周角等于它所对的圆心角的
一半
.
推论1:同弧或等弧所对的圆周角
相等
.
推论2:半圆(或直径)所对的圆周角是
直角
,90°的圆周角所对的弦是
直径
.
活动4
典例赏析及练习
例1
如图,点A,B,C都在⊙O上,∠AOC=130°,∠ACB=40°,则∠BOC=
50°
.
例2
如图,BC是⊙O的弦,OA⊥BC,∠AOB=55°,则∠ADC的度数是(
C
)
A.55°
B.45°
C.27.5°
D.25°
例3
教材第87页
例4.
涉及直径时,通常利用“直径所对的圆周角是直角”来构造直角三角形,并借助直角三角形的性质来解决问题.
练习:
1.教材第88页
练习第1题.
2.如图,AB是⊙O的直径,C,D是⊙O上的两点,且AC=CD.连接BC,BD,若∠CBD=20°,则∠A=
70
°.
3.如图,A,D是⊙O上的两点,BC是直径,若∠D=40°,则∠ACO=(
D
)
A.80°
B.70°
C.60°
D.50°
4.教材第88页
练习第3题.
5.如图,AB是⊙O的直径,CD是⊙O的弦,如果∠ACD=30°.
(1)求∠BAD的度数;
(2)若AD=,求BD的长.
【答案】解:(1)∵AB是⊙O的直径,∴∠ADB=90°.
∵∠B=∠ACD=30°,∴∠BAD=90°-∠B=60°;
(2)在Rt△ADB中,∵∠B=30°,∴AD=AB.
∴AB=,BD==3.
活动5
课堂小结
1.圆周角的概念.
2.圆周角定理及推论.
四、作业布置与教学反思
第2课时
圆内接四边形
一、教学目标
1.掌握圆内接多边形、多边形的外接圆的概念.
2.理解圆内接四边形的性质.
3.通过探究圆内接四边形的性质,发展学生的推理能力.
二、教学重难点
重点
圆内接四边形对角互补的探索与运用.
难点
圆内接四边形性质的灵活应用以及添加辅助线.
重难点解读
圆内接四边形的对角互补,并且任何一个外角都等于它的内对角.
三、教学过程
活动1
旧知回顾
1.回顾圆周角定理及其两个推论.
2.如图,点C在以AB为直径的⊙O上,AB=10
cm,∠A=30°,则BC的长为_________cm.
3.如图,点A,B,C在⊙O上,连接OA,OB,若∠ABO=25°,则∠C=_________.
活动2
探究新知
教材第87页
思考.
提出问题:
(1)图24.1-17中,∠A是圆周角吗?∠ABC,∠C,∠ADC呢?
(2)∠A与∠C,∠ABC与∠ADC之间有什么关系?用圆周角定理尝试证明;
(3)由此你能得出圆内接四边形的什么结论?
活动3
知识归纳
1.如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的
外接圆
.
2.圆内接四边形的对角
互补
.
活动4
典例赏析及练习
例1
如图,四边形ABCD内接于⊙O,E为CD延长线上一点,若∠B=100°,则∠ADE=
100°
.
例2
如图,点A,B,C,D四个点均在⊙O上,∠A=70°,则∠C为(
C
)
A.35°
B.70°
C.110°
D.120°
练习:
1.如图,四边形ABCD是⊙O的内接四边形,∠BOD=100°,则∠BCD=
130
°.
2.圆内接四边形ABCD中,∠A∶∠B∶∠C=2∶3∶7,则∠D=
120
°.
3.如图,四边形ABCD是⊙O的内接四边形,AB=AD,若∠C=68°,则∠ABD为(
A
)
A.34°
B.56°
C.68°
D.112°
4.如图,四边形ABCD是⊙O的内接四边形,∠ABC=60°,点D是的中点,点E在OC的延长线上,且CE=AD,连接DE.求证:四边形AOCD是菱形.
【答案】证明:如图,连接OD.
∵点D是的中点,∴=.
∴AD=DC,∠AOD=∠DOC.
∵∠AOC=2∠ABC=120°,∴∠AOD=∠DOC=60°.
∵OC=OD,∴OA=OC=CD=AD,
∴四边形AOCD是菱形.
活动5
课堂小结
1.圆内接多边形和多边形外接圆的概念.
2.圆内接四边形的性质.
四、作业布置与教学反思
圆周角
第1课时
圆周角定理及推论
一、教学目标
1.理解圆周角的概念,识别圆心角和圆周角.
2.理解圆周角定理及其推论.
3.熟练掌握圆周角定理及其推论的灵活运用.
二、教学重难点
重点
掌握圆周角定理和推论及运用.
难点
运用分类思想证明圆周角定理.
重难点解读
1.圆周角定理及其推论1成立的前提是在同圆或等圆中.
2.在同圆或等圆中,如果两个圆周角相等,那么它们所对的弧相等,所对的弦也相等.
3.由圆周角定理推论2可知,如果一个三角形一条边上的中线等于这条边的一半,那么这个三角形是以这条边为斜边的直角三角形.
4.求一条弦所对的圆周角的度数时,应注意这条弦所对的圆周角有两种情况.
5.在同圆或等圆中,一条弦两侧所对的两个圆周角的度数之和是180°.
6.圆心角与圆周角是圆内经常出现的两种角,巧用“一条弧所对的圆周角是它所对的圆心角的一半”这一结论,可以帮助我们实现圆周角与圆心角之间的转化.
三、教学过程
活动1
旧知回顾
1.什么叫圆心角?
2.圆心角、弦、弧之间有什么内在联系?
3.如图,已知AB是⊙O的直径,C,D是的三等分点,∠AOE=60°,则∠COE的大小是(
)
A.40°
B.60°
C.80°
D.120°
活动2
探究新知
1.将圆心角的顶点进行移动,如图1.
(1)当角的顶点在圆心时,我们知道这样的角叫圆心角,如∠AOB.当角的顶点运动到圆周时,如∠ACB.∠ACB有什么特点?它与∠AOB有何异同?
(2)观察图2,你能仿照圆心角的定义给这类角取一个名字并下个定义吗?
(3)比较概念:圆心角定义中为什么没有提到“两边都与圆相交”呢?
2.教材第85页
探究.
提出问题:
(1)经过测量,图24.1-11中的圆周角∠ACB和圆心角∠AOB之间有什么关系?
(2)任意作一个圆,任取一条弧,作出它所对的圆周角与圆心角,测量它们的度数,你发现什么规律?
(3)一条弧所对的圆心角有几个?所对的圆周角有几个?
(4)改变动点C在圆周上的位置,看看圆周角的度数有没有变化?你发现了什么?
(5)如果把上述发现的结论中的“同弧”改为“等弧”,结论还正确吗?
(6)观察下图,BC是⊙O的直径.请问:BC所对的圆周角∠BAC是锐角、直角还是钝角?
(7)如图,若圆周角∠BAC=90°,那么它所对的弦BC经过圆心吗?为什么?由此能得出什么结论?
活动3
知识归纳
1.顶点在圆上,并且两边都与圆相交的角叫做圆周角.
2.圆周角定理:一条弧所对的圆周角等于它所对的圆心角的
一半
.
推论1:同弧或等弧所对的圆周角
相等
.
推论2:半圆(或直径)所对的圆周角是
直角
,90°的圆周角所对的弦是
直径
.
活动4
典例赏析及练习
例1
如图,点A,B,C都在⊙O上,∠AOC=130°,∠ACB=40°,则∠BOC=
50°
.
例2
如图,BC是⊙O的弦,OA⊥BC,∠AOB=55°,则∠ADC的度数是(
C
)
A.55°
B.45°
C.27.5°
D.25°
例3
教材第87页
例4.
涉及直径时,通常利用“直径所对的圆周角是直角”来构造直角三角形,并借助直角三角形的性质来解决问题.
练习:
1.教材第88页
练习第1题.
2.如图,AB是⊙O的直径,C,D是⊙O上的两点,且AC=CD.连接BC,BD,若∠CBD=20°,则∠A=
70
°.
3.如图,A,D是⊙O上的两点,BC是直径,若∠D=40°,则∠ACO=(
D
)
A.80°
B.70°
C.60°
D.50°
4.教材第88页
练习第3题.
5.如图,AB是⊙O的直径,CD是⊙O的弦,如果∠ACD=30°.
(1)求∠BAD的度数;
(2)若AD=,求BD的长.
【答案】解:(1)∵AB是⊙O的直径,∴∠ADB=90°.
∵∠B=∠ACD=30°,∴∠BAD=90°-∠B=60°;
(2)在Rt△ADB中,∵∠B=30°,∴AD=AB.
∴AB=,BD==3.
活动5
课堂小结
1.圆周角的概念.
2.圆周角定理及推论.
四、作业布置与教学反思
第2课时
圆内接四边形
一、教学目标
1.掌握圆内接多边形、多边形的外接圆的概念.
2.理解圆内接四边形的性质.
3.通过探究圆内接四边形的性质,发展学生的推理能力.
二、教学重难点
重点
圆内接四边形对角互补的探索与运用.
难点
圆内接四边形性质的灵活应用以及添加辅助线.
重难点解读
圆内接四边形的对角互补,并且任何一个外角都等于它的内对角.
三、教学过程
活动1
旧知回顾
1.回顾圆周角定理及其两个推论.
2.如图,点C在以AB为直径的⊙O上,AB=10
cm,∠A=30°,则BC的长为_________cm.
3.如图,点A,B,C在⊙O上,连接OA,OB,若∠ABO=25°,则∠C=_________.
活动2
探究新知
教材第87页
思考.
提出问题:
(1)图24.1-17中,∠A是圆周角吗?∠ABC,∠C,∠ADC呢?
(2)∠A与∠C,∠ABC与∠ADC之间有什么关系?用圆周角定理尝试证明;
(3)由此你能得出圆内接四边形的什么结论?
活动3
知识归纳
1.如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的
外接圆
.
2.圆内接四边形的对角
互补
.
活动4
典例赏析及练习
例1
如图,四边形ABCD内接于⊙O,E为CD延长线上一点,若∠B=100°,则∠ADE=
100°
.
例2
如图,点A,B,C,D四个点均在⊙O上,∠A=70°,则∠C为(
C
)
A.35°
B.70°
C.110°
D.120°
练习:
1.如图,四边形ABCD是⊙O的内接四边形,∠BOD=100°,则∠BCD=
130
°.
2.圆内接四边形ABCD中,∠A∶∠B∶∠C=2∶3∶7,则∠D=
120
°.
3.如图,四边形ABCD是⊙O的内接四边形,AB=AD,若∠C=68°,则∠ABD为(
A
)
A.34°
B.56°
C.68°
D.112°
4.如图,四边形ABCD是⊙O的内接四边形,∠ABC=60°,点D是的中点,点E在OC的延长线上,且CE=AD,连接DE.求证:四边形AOCD是菱形.
【答案】证明:如图,连接OD.
∵点D是的中点,∴=.
∴AD=DC,∠AOD=∠DOC.
∵∠AOC=2∠ABC=120°,∴∠AOD=∠DOC=60°.
∵OC=OD,∴OA=OC=CD=AD,
∴四边形AOCD是菱形.
活动5
课堂小结
1.圆内接多边形和多边形外接圆的概念.
2.圆内接四边形的性质.
四、作业布置与教学反思
同课章节目录
