2020-2021学年人教版七年级数学下册第10章数据的收集、整理、描述 单元综合提升-(word含答案)
文档属性
| 名称 | 2020-2021学年人教版七年级数学下册第10章数据的收集、整理、描述 单元综合提升-(word含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 268.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-06 11:35:39 | ||
图片预览




文档简介
2021年人教版七年级数学下册《第10章数据的收集、整理、描述》单元同步训练(附答案)
1.某烟花爆竹厂从20万件同类产品中随机抽取了100件进行质检,发现其中有10件不合格,那么你估计该厂这20万件产品中合格品约为( )
A.2万件 B.16万件 C.18万件 D.10万件
2.下列调查中,适宜采用全面调查的是( )
A.调查全国初中学生身高情况
B.调查沈阳浑河流域水质情况
C.调查某品牌汽车的抗撞击情况
D.了解某班女同学800米的成绩情况
3.为了解新冠肺炎疫情解封后刚复学时学生的心理健康,某中学在2000名同学中随机抽查了500名同学进行问卷调查,则本次调查的样本容量是( )
A.500 B.500名 C.2000 D.2000名
4.某校为了了解全校1500名学生家长对“禁止学生带手机进入校园”这一规定的意见,随机对全校100名学生家长进行调查,这一问题中样本的容量是( )
A.1500
B.受调查的全校1500名学生家长的意见
C.被抽取的100名学生家长的意见
D.100
5.以下调查中适宜进行全面调查的是( )
A.调查某批汽车的扛撞能力
B.了解某班同学的体重
C.了解全国15岁至18岁少年的健康状况
D.调查某批节能灯使用寿命
6.下列调查方式合适的是( )
A.疫情期间,为了解进校人员体温情况采用抽样调查的方式
B.了解炮弹的杀伤力,采用全面调查的方式
C.对中央台“新闻联播”收视率的调查,采用全面调查的方式
D.对哒吽小镇食品合格情况的调查,采用抽样调查的方式
7.醴陵市“师生诗词大赛”成绩结果统计如表,成绩在91﹣100分的为优秀,则优秀的频率是( )
分数段 61﹣﹣70 71﹣﹣80 81﹣﹣90 91﹣﹣100
人数(人) 2 8 6 4
A.0.2 B.0.25 C.0.3 D.0.35
8.老师将某班一次数学测试成绩分为A,B,C,D四个等级,绘制成如图所示的扇形统计图,则C等级所占的百分比为( )
A.10% B.15% C.20% D.25%
9.去年我市有3500名考生参加中考,为了了解这些考生的数学成绩,从中抽取1000名考生的数学成绩进行统计分析,在这个调查中,下列说法:①这3500名考生的数学中考成绩的全体是总体;②每个考生是个体;③1000名考生是总体的一个样本;④样本容量是1000.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
10.足球运动是全球体育界最具响力的单项体育场动,故有世界第一大运动的美称,为了解某学校校园足球与学生数占学校总人数的百分比,最合适的统计方式是( )
A.折线统计图 B.条形统计图 C.扇形统计图 D.直方图
11.为了解我市七年级男生的体重分布情况,市教育局从各学校共随机抽取了500名七年级男生进行了测量.在这个问题中,样本容量是 .
12.在频数分布直方图中,有11个小长方形,若中间一个小长方形的面积等于其它10个小长方形面积和的,频数分布直方图中有150个数据,则中间一组的频数为 .
13.我们把一个样本的40个数据分成4组,其中第1、2、3组的频数分别为6、12、14,则第4组的频率为 .
14.某校为了解七年级学生的身体素质情况,从七年级各班随机抽取了数量相同的男生和女生,组成一个容量为60的样本,进行各项体育项目的测试.下表是通过整理样本数据,得到的关于每个个体测试成绩的部分统计表:
某校60名学生体育测试成绩频数分布表
成绩 划记 频数 百分比
优秀
a 30%
良好
30 b
合格
9 15%
不合格
3 5%
合计 60 60 100%
如果该校七年级共有300名学生,根据以上数据,估计该校七年级学生身体素质良好及以上的人数为 人.
15.某校学生参加体育兴趣小组情况的统计图如图所示,若参加人数最多的小组有80人,则参加人数最少的小组有 人.
16.为了了解本校九年级学生的体能情况,随机抽查了其中30名学生,测试1分钟仰卧起坐的次数,并将其绘制成如图所示的频数直方图,那么仰卧起坐次数在25~30次的人数占抽查总人数的百分比是 .
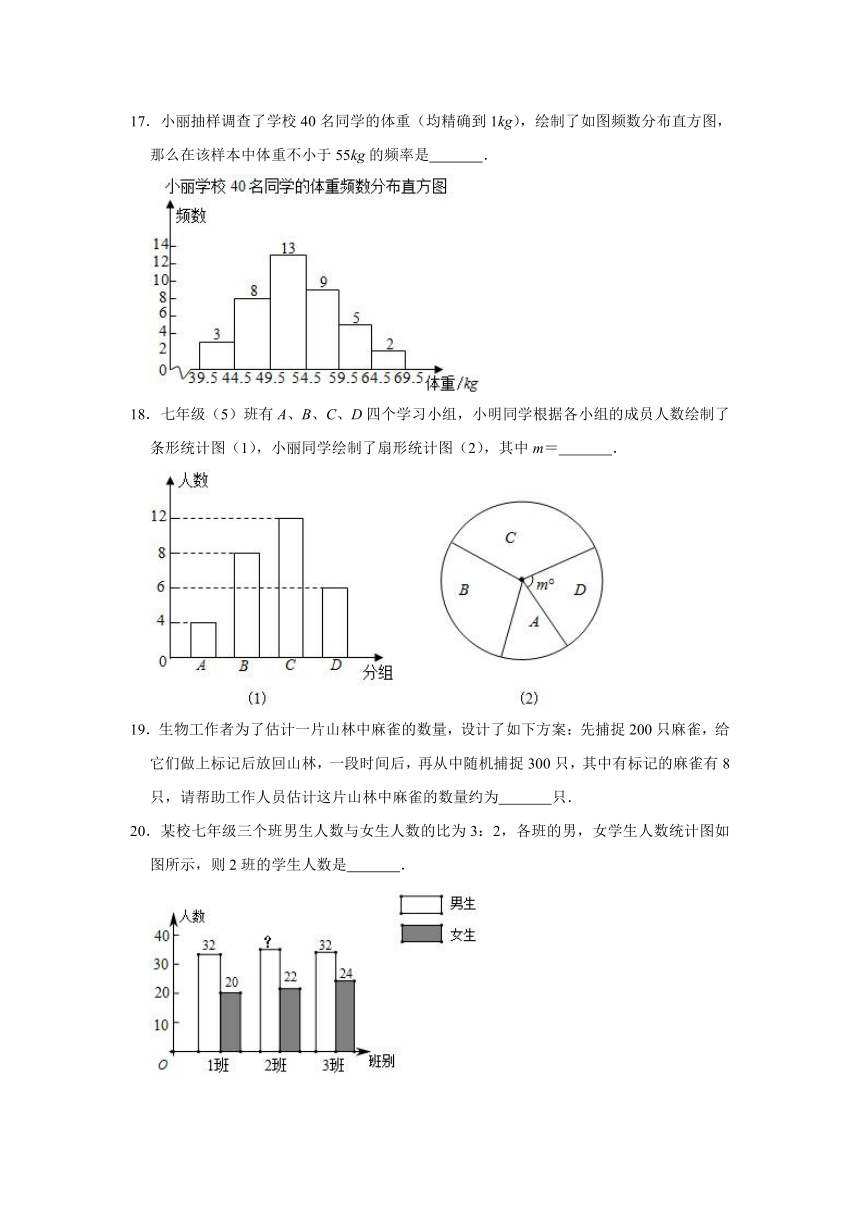
17.小丽抽样调查了学校40名同学的体重(均精确到1kg),绘制了如图频数分布直方图,那么在该样本中体重不小于55kg的频率是 .
18.七年级(5)班有A、B、C、D四个学习小组,小明同学根据各小组的成员人数绘制了条形统计图(1),小丽同学绘制了扇形统计图(2),其中m= .
19.生物工作者为了估计一片山林中麻雀的数量,设计了如下方案:先捕捉200只麻雀,给它们做上标记后放回山林,一段时间后,再从中随机捕捉300只,其中有标记的麻雀有8只,请帮助工作人员估计这片山林中麻雀的数量约为 只.
20.某校七年级三个班男生人数与女生人数的比为3:2,各班的男,女学生人数统计图如图所示,则2班的学生人数是 .
21.每年夏天全国各地总有未成年人因溺水而丧失生命,令人痛心疾首.今年某中学为确保学生安全,开展了“远离溺水,珍爱生命”的防溺水安全竞赛,学校对参加比赛的学生获奖情况进行了统计,绘制了两幅不完整的统计图,请结合图中相关数据解答下列问题.
(1)求参加此安全竞赛的学生共有多少人;
(2)在扇形统计图中,“三等奖”所对应的扇形的圆心角的度数为多少度?
(3)求获得二等奖的人数,并将条形统计图补充完整.
22.世界卫生组织在2020年3月11日表示,新冠肺炎疫情的爆发已经构成一次全球性“大流行”.面对全国人民齐心协力的防疫抗疫工作,我们中学生也应认真学习各种防疫知识,保护好自己和家人.某中学组织七年级全体学生500人进行了一次“新型冠状病毒肺炎防疫知识”竞赛,赛后随机抽取了部分学生成绩进行统计,制作了如下统计表和频数直方图.请根据图表中提供的信息,解答下列问题:
分数段(x表示分数) 频数 百分比
50≤x<60 4 10%
60≤x<70 8 b
70≤x<80 a 30%
80≤x<90 10 25%
90≤x<100 6 15%
(1)表中a= ,b= ,并补全频数直方图;
(2)若用扇形统计图描述成绩分布情况,则分数段60≤x<70对应扇形的圆心角度数是 °;
(3)请估计该年级分数段80≤x<100内的学生有多少人.
23.光明中学为了解学生上学的交通方式,现从全校学生中随机抽取了部分学生进行“我上学的交通方式”问卷调查,规定每人必须并且只能在“乘车”、“步行”、“骑车”和“其他”四项中选择一项,并将统计结果绘制了两幅不完整的统计图.
请解答下列问题:
(1)在这次调查中,该学校一共抽样调查了 名学生;
(2)在扇形统计图中“骑车”一项对应的扇形圆心角的度数是 °;
(3)补全条形统计图;
(4)若该学校共有1800名学生,试估计该学校学生中选择“步行”方式的人数.
24.“精准扶贫”这是新时期党和国家扶贫工作的精髓和亮点,某校团委随机抽取七年级部分学生,对他们是否了解关于“精准扶贫”的情况进行调查,调查结果有三种:A、了解很多;B、了解一点;C、不了解.团委根据调查的数据进行整理,绘制了尚不完整的统计图如图,图1中C区域的圆心角为36°,请根据统计图中的相关的信息,解答下列问题
(1)求本次活动共调查了 名学生;图1中,B区域的圆心角的度数是 ;
(2)补全条形统计图.
(3)若该校七年级有2100名学生,请估算该校不是“了解很多”的学生人数.
25.某校数学活动小组对经过某路段的小型汽车每车乘坐人数(含驾驶员)进行了随机调查,根据每车乘坐人数,把乘坐1人、2人、3人、4人、5人的车分别记为A,B,C,D,E五类,由调查所得数据绘制了如图所示的两幅不完整的统计图.
(1)本次调查的小型汽车共 辆,扇形统计图中A类对应的圆心角度数为 ,E类对应的圆心角度数为 .
(2)补全条形统计图;
(3)若某时段通过该路段的小型汽车数量为5000辆,请你估计其中只乘坐1人的小型汽车数量.
26.促进青少年健康成长是实施“健康中国”战略的重要内容.为了引导学生积极参与体育运动,某校举办了一分钟跳绳比赛,随机抽取了40名学生一分钟跳绳的次数进行调查统计,并根据调查统计结果绘制了如图表格和统计图:
等级 次数 频数
不合格 100≤x<120 4
合格 120≤x<140 a
良好 140≤x<160 12
优秀 160≤x<180 b
请结合上述信息完成下列问题:
(1)a= ,b= ;
(2)请补全频数分布直方图;
(3)在扇形统计图中,“良好”等级对应的圆心角的度数是 ;
(4)若该校有2000名学生,根据抽样调查结果,请估计该校学生一分钟跳绳次数达到合格及以上的人数.
27.为响应教育部“停课不停学”的号召,某中学组织本校优秀教师开展线上教学,经过近三个月的线上授课后,在五月初复学.该校为了解学生不同阶段学习效果,决定随机抽取七年级部分学生进行两次跟踪测评,第一次是复学初对线上教学质量测评,第二次是复学一个月后教学质量测评.根据第一次测试的数学成绩制成频数直方图:
复学一个月后,根据第二次测试的数学成绩得到如下统计表
成绩 30≤x<40 40≤x<50 50≤x<60 60≤x<70 70≤x<80 80≤x<90 90≤x<100
人数 1 3 3 m 15 14 6
根据以上图表信息,完成下列问题:
(1)m= ;
(2)请在图中作出两次测试的数学成绩折线图;
(3)请估计复学一个月后该校600名七年级学生数学成绩合格(60分及以上)的人数.
参考答案
1.解:该厂这20万件产品中合格品约为:(100﹣10)÷100×100%×20=18(万件).
故选:C.
2.解:A.调查全国初中学生身高情况,适宜抽样调查,故本选项不合题意;
B.调查沈阳浑河流域水质情况,适宜抽样调查,故本选项不符合题意;
C.调查某品牌汽车的抗撞击情况,适宜抽样调查,故本选项不符合题意;
D.了解某班女同学800米的成绩情况,是准确的调查,适于全面调查,故本选项符合题意;
故选:D.
3.解:为了解新冠肺炎疫情解封后刚复学时学生的心理健康,某中学在2000名同学中随机抽查了500名同学进行问卷调查,则本次调查的样本容量是500.
故选:A.
4.解:某校为了了解全校1500名学生家长对“禁止学生带手机进入校园”这一规定的意见,随机对全校100名学生家长进行调查,这一问题中样本的容量是100.
故选:D.
5.解:A.调查某批汽车的扛撞能力,适合使用抽样调查,故本选项不合题意;
B.了解某班同学的体重,适合使用全面调查,故本选项符合题意;
C.了解全国15岁至18岁少年的健康状况,适合使用抽样调查,故本选项不合题意;
D.调查某批节能灯使用寿命,适合使用抽样调查,故本选项不合题意;
故选:B.
6.解:A、疫情期间,为了解进校人员体温情况,适合进行全面调查,故本选项不合题意;
B、了解炮弹的杀伤力,适合抽样调查,故本选项不合题意;
C、对中央台“新闻联播”收视率的调查,适合抽样调查,故本选项不合题意;
D、对哒吽小镇食品合格情况的调查,适合抽样调查,故本选项符合题意.
故选:D.
7.解:由表格中数据可得,优秀的频率是:=0.2.
故选:A.
8.解:C等级所占的百分比为:1﹣20%﹣35%﹣30%=15%.
故选:B.
9.解:①这3500名考生的数学中考成绩的全体是总体,此结论正确;
②每个考生的数学成绩是个体,此结论错误;
③1000名考生的数学成绩是总体的一个样本,此结论错误;
④样本容量是1000,此结论正确.
故选:C.
10.解:为了解某学校校园足球与学生数占学校总人数的百分比,最合适的统计方式是扇形统计图,
故选:C.
11.解:本题的样本是500名七年级男生的体重,故样本容量是500.
故答案为:500.
12.解:设中间一个小长方形的面积为x,
则x+4x=1,
解得:x=,
150×=30,
故答案为:30.
13.解:第4组的频数为:40﹣6﹣12﹣14=8,
频率为:=0.2,
故答案为:0.2.
14.解:根据频数分布表可知:
9÷15%=60,
∴a=60×30%=18,
b=1﹣30%﹣15%﹣5%=50%,
∴300×(30%+50%)=240(人).
答:估计该校七年级学生身体素质良好及以上的人数为240人.
故答案为:240.
15.解:由扇形统计图可得,
参加乒乓球的学生所占的百分比为:1﹣35%﹣25%=40%,
∵参加人数最多的小组有80人,
∴参加体育兴趣小组的学生有:80÷40%=200(人),
∴参加人数最少的小组有200×25%=50(人),
故答案为:50.
16.解:×100%=40%,
即仰卧起坐次数在25~30次的人数占抽查总人数的百分比是40%,
故答案为:40%.
17.解:观察直方图可知:
因为该样本中体重不小于55kg的频数为:9+5+2=16,
所以该样本中体重不小于55kg的频率是=0.4.
故答案为:0.4.
18.解:m=360×=72,
答:m=72,
故答案为:72.
19.解:200÷=7500(只),
即这片山林中麻雀的数量约为7500只,
故答案为:7500.
20.解:由条形图知,七年级共有女生20+22+24=66(人).
因为七年级男生人数与女生人数的比为3:2,
所以七年级共有男人66÷=99(人).
所以2班有男生99﹣32﹣32=35(人).
所以2班共有学生35+22=57(人).
故答案为:57人.
21.解:(1)由题意可得,
18÷45%=40(人),
即参加此安全竞赛的学生共有40人;
(2)360°×=90°,
即在扇形统计图中,“三等奖”所对应的扇形的圆心角的度数为90度;
(3)获得二等奖的有40×20%=8(人),
补充完整的条形统计图如右图所示.
22.解:(1)本次抽取的学生有:4÷10%=40(人),
a=40×30%=12,b=8÷40×100%=20%,
故答案为:12,20%,
补全的频数直方图如右图所示;
(2)分数段60≤x<70对应扇形的圆心角度数是:360°×=72°,
故答案为:72;
(3)500×(25%+15%)
=500×40%
=200(人),
即估计该年级分数段80≤x<100内的学生有200人.
23.解:(1)本次调查中,该学校调查的学生人数为(20+5)÷50%=50人,
故答案为:50;
(2)在扇形统计图中“骑车”一项对应的扇形圆心角的度数是360°×=72°,
故答案为:72;
(3)步行的人数为50﹣(20+10+5)=15(人),
补全图形如下:
(4)估计该学校学生中选择“步行”方式的人数为1800×=540(人).
24.解:(1)本次活动共调查了:20÷=200名学生,
B区域的圆心角度是:360°×=108°,
故答案为:200,108°;
(2)调查结果为B的学生有:200﹣120﹣20=60(人),
补全的条形统计图如右图所示;
(3)2100×=840(人),
即估算该校不是“了解很多”的学生有840人.
25.解:(1)由图象可得,
本次调查的小型汽车共32÷20%=160(辆),
扇形统计图中A类对应的圆心角度数为:360°×=108°,
E类对应的圆心角度数为360°×=18°,
故答案为:160,108°,18°;
(2)B类有:160×35%=56(辆),D类有:160﹣48﹣56﹣32﹣8=16(辆),
补全的条形统计图如右图所示;
(3)5000×=1500(辆),
答:估计其中只乘坐1人的小型汽车的有1500辆.
26.解:(1)b=40×25%=10,
则a=40﹣(4+12+10)=14,
故答案为:14、10;
(2)补全频数分布直方图如下:
(3)在扇形统计图中,“良好”等级对应的圆心角的度数是360°×=108°,
故答案为:108°;
(4)估计该校学生一分钟跳绳次数达到合格及以上的人数为2000×=1800(人).
27.解:(1)由图1可知,随机抽取的学生有2+8+10+15+10+4+1=50(人),
故m=50﹣(1+3+3+15+14+6)=50﹣42=8,
故答案为:8;
(2)两次测试的数学成绩折线图如下图所示;
(3)600×=600×=600×=516(人),
答:估计复学一个月后该校600名七年级学生数学成绩合格(60分及以上)的有516人
1.某烟花爆竹厂从20万件同类产品中随机抽取了100件进行质检,发现其中有10件不合格,那么你估计该厂这20万件产品中合格品约为( )
A.2万件 B.16万件 C.18万件 D.10万件
2.下列调查中,适宜采用全面调查的是( )
A.调查全国初中学生身高情况
B.调查沈阳浑河流域水质情况
C.调查某品牌汽车的抗撞击情况
D.了解某班女同学800米的成绩情况
3.为了解新冠肺炎疫情解封后刚复学时学生的心理健康,某中学在2000名同学中随机抽查了500名同学进行问卷调查,则本次调查的样本容量是( )
A.500 B.500名 C.2000 D.2000名
4.某校为了了解全校1500名学生家长对“禁止学生带手机进入校园”这一规定的意见,随机对全校100名学生家长进行调查,这一问题中样本的容量是( )
A.1500
B.受调查的全校1500名学生家长的意见
C.被抽取的100名学生家长的意见
D.100
5.以下调查中适宜进行全面调查的是( )
A.调查某批汽车的扛撞能力
B.了解某班同学的体重
C.了解全国15岁至18岁少年的健康状况
D.调查某批节能灯使用寿命
6.下列调查方式合适的是( )
A.疫情期间,为了解进校人员体温情况采用抽样调查的方式
B.了解炮弹的杀伤力,采用全面调查的方式
C.对中央台“新闻联播”收视率的调查,采用全面调查的方式
D.对哒吽小镇食品合格情况的调查,采用抽样调查的方式
7.醴陵市“师生诗词大赛”成绩结果统计如表,成绩在91﹣100分的为优秀,则优秀的频率是( )
分数段 61﹣﹣70 71﹣﹣80 81﹣﹣90 91﹣﹣100
人数(人) 2 8 6 4
A.0.2 B.0.25 C.0.3 D.0.35
8.老师将某班一次数学测试成绩分为A,B,C,D四个等级,绘制成如图所示的扇形统计图,则C等级所占的百分比为( )
A.10% B.15% C.20% D.25%
9.去年我市有3500名考生参加中考,为了了解这些考生的数学成绩,从中抽取1000名考生的数学成绩进行统计分析,在这个调查中,下列说法:①这3500名考生的数学中考成绩的全体是总体;②每个考生是个体;③1000名考生是总体的一个样本;④样本容量是1000.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
10.足球运动是全球体育界最具响力的单项体育场动,故有世界第一大运动的美称,为了解某学校校园足球与学生数占学校总人数的百分比,最合适的统计方式是( )
A.折线统计图 B.条形统计图 C.扇形统计图 D.直方图
11.为了解我市七年级男生的体重分布情况,市教育局从各学校共随机抽取了500名七年级男生进行了测量.在这个问题中,样本容量是 .
12.在频数分布直方图中,有11个小长方形,若中间一个小长方形的面积等于其它10个小长方形面积和的,频数分布直方图中有150个数据,则中间一组的频数为 .
13.我们把一个样本的40个数据分成4组,其中第1、2、3组的频数分别为6、12、14,则第4组的频率为 .
14.某校为了解七年级学生的身体素质情况,从七年级各班随机抽取了数量相同的男生和女生,组成一个容量为60的样本,进行各项体育项目的测试.下表是通过整理样本数据,得到的关于每个个体测试成绩的部分统计表:
某校60名学生体育测试成绩频数分布表
成绩 划记 频数 百分比
优秀
a 30%
良好
30 b
合格
9 15%
不合格
3 5%
合计 60 60 100%
如果该校七年级共有300名学生,根据以上数据,估计该校七年级学生身体素质良好及以上的人数为 人.
15.某校学生参加体育兴趣小组情况的统计图如图所示,若参加人数最多的小组有80人,则参加人数最少的小组有 人.
16.为了了解本校九年级学生的体能情况,随机抽查了其中30名学生,测试1分钟仰卧起坐的次数,并将其绘制成如图所示的频数直方图,那么仰卧起坐次数在25~30次的人数占抽查总人数的百分比是 .
17.小丽抽样调查了学校40名同学的体重(均精确到1kg),绘制了如图频数分布直方图,那么在该样本中体重不小于55kg的频率是 .
18.七年级(5)班有A、B、C、D四个学习小组,小明同学根据各小组的成员人数绘制了条形统计图(1),小丽同学绘制了扇形统计图(2),其中m= .
19.生物工作者为了估计一片山林中麻雀的数量,设计了如下方案:先捕捉200只麻雀,给它们做上标记后放回山林,一段时间后,再从中随机捕捉300只,其中有标记的麻雀有8只,请帮助工作人员估计这片山林中麻雀的数量约为 只.
20.某校七年级三个班男生人数与女生人数的比为3:2,各班的男,女学生人数统计图如图所示,则2班的学生人数是 .
21.每年夏天全国各地总有未成年人因溺水而丧失生命,令人痛心疾首.今年某中学为确保学生安全,开展了“远离溺水,珍爱生命”的防溺水安全竞赛,学校对参加比赛的学生获奖情况进行了统计,绘制了两幅不完整的统计图,请结合图中相关数据解答下列问题.
(1)求参加此安全竞赛的学生共有多少人;
(2)在扇形统计图中,“三等奖”所对应的扇形的圆心角的度数为多少度?
(3)求获得二等奖的人数,并将条形统计图补充完整.
22.世界卫生组织在2020年3月11日表示,新冠肺炎疫情的爆发已经构成一次全球性“大流行”.面对全国人民齐心协力的防疫抗疫工作,我们中学生也应认真学习各种防疫知识,保护好自己和家人.某中学组织七年级全体学生500人进行了一次“新型冠状病毒肺炎防疫知识”竞赛,赛后随机抽取了部分学生成绩进行统计,制作了如下统计表和频数直方图.请根据图表中提供的信息,解答下列问题:
分数段(x表示分数) 频数 百分比
50≤x<60 4 10%
60≤x<70 8 b
70≤x<80 a 30%
80≤x<90 10 25%
90≤x<100 6 15%
(1)表中a= ,b= ,并补全频数直方图;
(2)若用扇形统计图描述成绩分布情况,则分数段60≤x<70对应扇形的圆心角度数是 °;
(3)请估计该年级分数段80≤x<100内的学生有多少人.
23.光明中学为了解学生上学的交通方式,现从全校学生中随机抽取了部分学生进行“我上学的交通方式”问卷调查,规定每人必须并且只能在“乘车”、“步行”、“骑车”和“其他”四项中选择一项,并将统计结果绘制了两幅不完整的统计图.
请解答下列问题:
(1)在这次调查中,该学校一共抽样调查了 名学生;
(2)在扇形统计图中“骑车”一项对应的扇形圆心角的度数是 °;
(3)补全条形统计图;
(4)若该学校共有1800名学生,试估计该学校学生中选择“步行”方式的人数.
24.“精准扶贫”这是新时期党和国家扶贫工作的精髓和亮点,某校团委随机抽取七年级部分学生,对他们是否了解关于“精准扶贫”的情况进行调查,调查结果有三种:A、了解很多;B、了解一点;C、不了解.团委根据调查的数据进行整理,绘制了尚不完整的统计图如图,图1中C区域的圆心角为36°,请根据统计图中的相关的信息,解答下列问题
(1)求本次活动共调查了 名学生;图1中,B区域的圆心角的度数是 ;
(2)补全条形统计图.
(3)若该校七年级有2100名学生,请估算该校不是“了解很多”的学生人数.
25.某校数学活动小组对经过某路段的小型汽车每车乘坐人数(含驾驶员)进行了随机调查,根据每车乘坐人数,把乘坐1人、2人、3人、4人、5人的车分别记为A,B,C,D,E五类,由调查所得数据绘制了如图所示的两幅不完整的统计图.
(1)本次调查的小型汽车共 辆,扇形统计图中A类对应的圆心角度数为 ,E类对应的圆心角度数为 .
(2)补全条形统计图;
(3)若某时段通过该路段的小型汽车数量为5000辆,请你估计其中只乘坐1人的小型汽车数量.
26.促进青少年健康成长是实施“健康中国”战略的重要内容.为了引导学生积极参与体育运动,某校举办了一分钟跳绳比赛,随机抽取了40名学生一分钟跳绳的次数进行调查统计,并根据调查统计结果绘制了如图表格和统计图:
等级 次数 频数
不合格 100≤x<120 4
合格 120≤x<140 a
良好 140≤x<160 12
优秀 160≤x<180 b
请结合上述信息完成下列问题:
(1)a= ,b= ;
(2)请补全频数分布直方图;
(3)在扇形统计图中,“良好”等级对应的圆心角的度数是 ;
(4)若该校有2000名学生,根据抽样调查结果,请估计该校学生一分钟跳绳次数达到合格及以上的人数.
27.为响应教育部“停课不停学”的号召,某中学组织本校优秀教师开展线上教学,经过近三个月的线上授课后,在五月初复学.该校为了解学生不同阶段学习效果,决定随机抽取七年级部分学生进行两次跟踪测评,第一次是复学初对线上教学质量测评,第二次是复学一个月后教学质量测评.根据第一次测试的数学成绩制成频数直方图:
复学一个月后,根据第二次测试的数学成绩得到如下统计表
成绩 30≤x<40 40≤x<50 50≤x<60 60≤x<70 70≤x<80 80≤x<90 90≤x<100
人数 1 3 3 m 15 14 6
根据以上图表信息,完成下列问题:
(1)m= ;
(2)请在图中作出两次测试的数学成绩折线图;
(3)请估计复学一个月后该校600名七年级学生数学成绩合格(60分及以上)的人数.
参考答案
1.解:该厂这20万件产品中合格品约为:(100﹣10)÷100×100%×20=18(万件).
故选:C.
2.解:A.调查全国初中学生身高情况,适宜抽样调查,故本选项不合题意;
B.调查沈阳浑河流域水质情况,适宜抽样调查,故本选项不符合题意;
C.调查某品牌汽车的抗撞击情况,适宜抽样调查,故本选项不符合题意;
D.了解某班女同学800米的成绩情况,是准确的调查,适于全面调查,故本选项符合题意;
故选:D.
3.解:为了解新冠肺炎疫情解封后刚复学时学生的心理健康,某中学在2000名同学中随机抽查了500名同学进行问卷调查,则本次调查的样本容量是500.
故选:A.
4.解:某校为了了解全校1500名学生家长对“禁止学生带手机进入校园”这一规定的意见,随机对全校100名学生家长进行调查,这一问题中样本的容量是100.
故选:D.
5.解:A.调查某批汽车的扛撞能力,适合使用抽样调查,故本选项不合题意;
B.了解某班同学的体重,适合使用全面调查,故本选项符合题意;
C.了解全国15岁至18岁少年的健康状况,适合使用抽样调查,故本选项不合题意;
D.调查某批节能灯使用寿命,适合使用抽样调查,故本选项不合题意;
故选:B.
6.解:A、疫情期间,为了解进校人员体温情况,适合进行全面调查,故本选项不合题意;
B、了解炮弹的杀伤力,适合抽样调查,故本选项不合题意;
C、对中央台“新闻联播”收视率的调查,适合抽样调查,故本选项不合题意;
D、对哒吽小镇食品合格情况的调查,适合抽样调查,故本选项符合题意.
故选:D.
7.解:由表格中数据可得,优秀的频率是:=0.2.
故选:A.
8.解:C等级所占的百分比为:1﹣20%﹣35%﹣30%=15%.
故选:B.
9.解:①这3500名考生的数学中考成绩的全体是总体,此结论正确;
②每个考生的数学成绩是个体,此结论错误;
③1000名考生的数学成绩是总体的一个样本,此结论错误;
④样本容量是1000,此结论正确.
故选:C.
10.解:为了解某学校校园足球与学生数占学校总人数的百分比,最合适的统计方式是扇形统计图,
故选:C.
11.解:本题的样本是500名七年级男生的体重,故样本容量是500.
故答案为:500.
12.解:设中间一个小长方形的面积为x,
则x+4x=1,
解得:x=,
150×=30,
故答案为:30.
13.解:第4组的频数为:40﹣6﹣12﹣14=8,
频率为:=0.2,
故答案为:0.2.
14.解:根据频数分布表可知:
9÷15%=60,
∴a=60×30%=18,
b=1﹣30%﹣15%﹣5%=50%,
∴300×(30%+50%)=240(人).
答:估计该校七年级学生身体素质良好及以上的人数为240人.
故答案为:240.
15.解:由扇形统计图可得,
参加乒乓球的学生所占的百分比为:1﹣35%﹣25%=40%,
∵参加人数最多的小组有80人,
∴参加体育兴趣小组的学生有:80÷40%=200(人),
∴参加人数最少的小组有200×25%=50(人),
故答案为:50.
16.解:×100%=40%,
即仰卧起坐次数在25~30次的人数占抽查总人数的百分比是40%,
故答案为:40%.
17.解:观察直方图可知:
因为该样本中体重不小于55kg的频数为:9+5+2=16,
所以该样本中体重不小于55kg的频率是=0.4.
故答案为:0.4.
18.解:m=360×=72,
答:m=72,
故答案为:72.
19.解:200÷=7500(只),
即这片山林中麻雀的数量约为7500只,
故答案为:7500.
20.解:由条形图知,七年级共有女生20+22+24=66(人).
因为七年级男生人数与女生人数的比为3:2,
所以七年级共有男人66÷=99(人).
所以2班有男生99﹣32﹣32=35(人).
所以2班共有学生35+22=57(人).
故答案为:57人.
21.解:(1)由题意可得,
18÷45%=40(人),
即参加此安全竞赛的学生共有40人;
(2)360°×=90°,
即在扇形统计图中,“三等奖”所对应的扇形的圆心角的度数为90度;
(3)获得二等奖的有40×20%=8(人),
补充完整的条形统计图如右图所示.
22.解:(1)本次抽取的学生有:4÷10%=40(人),
a=40×30%=12,b=8÷40×100%=20%,
故答案为:12,20%,
补全的频数直方图如右图所示;
(2)分数段60≤x<70对应扇形的圆心角度数是:360°×=72°,
故答案为:72;
(3)500×(25%+15%)
=500×40%
=200(人),
即估计该年级分数段80≤x<100内的学生有200人.
23.解:(1)本次调查中,该学校调查的学生人数为(20+5)÷50%=50人,
故答案为:50;
(2)在扇形统计图中“骑车”一项对应的扇形圆心角的度数是360°×=72°,
故答案为:72;
(3)步行的人数为50﹣(20+10+5)=15(人),
补全图形如下:
(4)估计该学校学生中选择“步行”方式的人数为1800×=540(人).
24.解:(1)本次活动共调查了:20÷=200名学生,
B区域的圆心角度是:360°×=108°,
故答案为:200,108°;
(2)调查结果为B的学生有:200﹣120﹣20=60(人),
补全的条形统计图如右图所示;
(3)2100×=840(人),
即估算该校不是“了解很多”的学生有840人.
25.解:(1)由图象可得,
本次调查的小型汽车共32÷20%=160(辆),
扇形统计图中A类对应的圆心角度数为:360°×=108°,
E类对应的圆心角度数为360°×=18°,
故答案为:160,108°,18°;
(2)B类有:160×35%=56(辆),D类有:160﹣48﹣56﹣32﹣8=16(辆),
补全的条形统计图如右图所示;
(3)5000×=1500(辆),
答:估计其中只乘坐1人的小型汽车的有1500辆.
26.解:(1)b=40×25%=10,
则a=40﹣(4+12+10)=14,
故答案为:14、10;
(2)补全频数分布直方图如下:
(3)在扇形统计图中,“良好”等级对应的圆心角的度数是360°×=108°,
故答案为:108°;
(4)估计该校学生一分钟跳绳次数达到合格及以上的人数为2000×=1800(人).
27.解:(1)由图1可知,随机抽取的学生有2+8+10+15+10+4+1=50(人),
故m=50﹣(1+3+3+15+14+6)=50﹣42=8,
故答案为:8;
(2)两次测试的数学成绩折线图如下图所示;
(3)600×=600×=600×=516(人),
答:估计复学一个月后该校600名七年级学生数学成绩合格(60分及以上)的有516人
