分式乘除法和加减法学案
图片预览



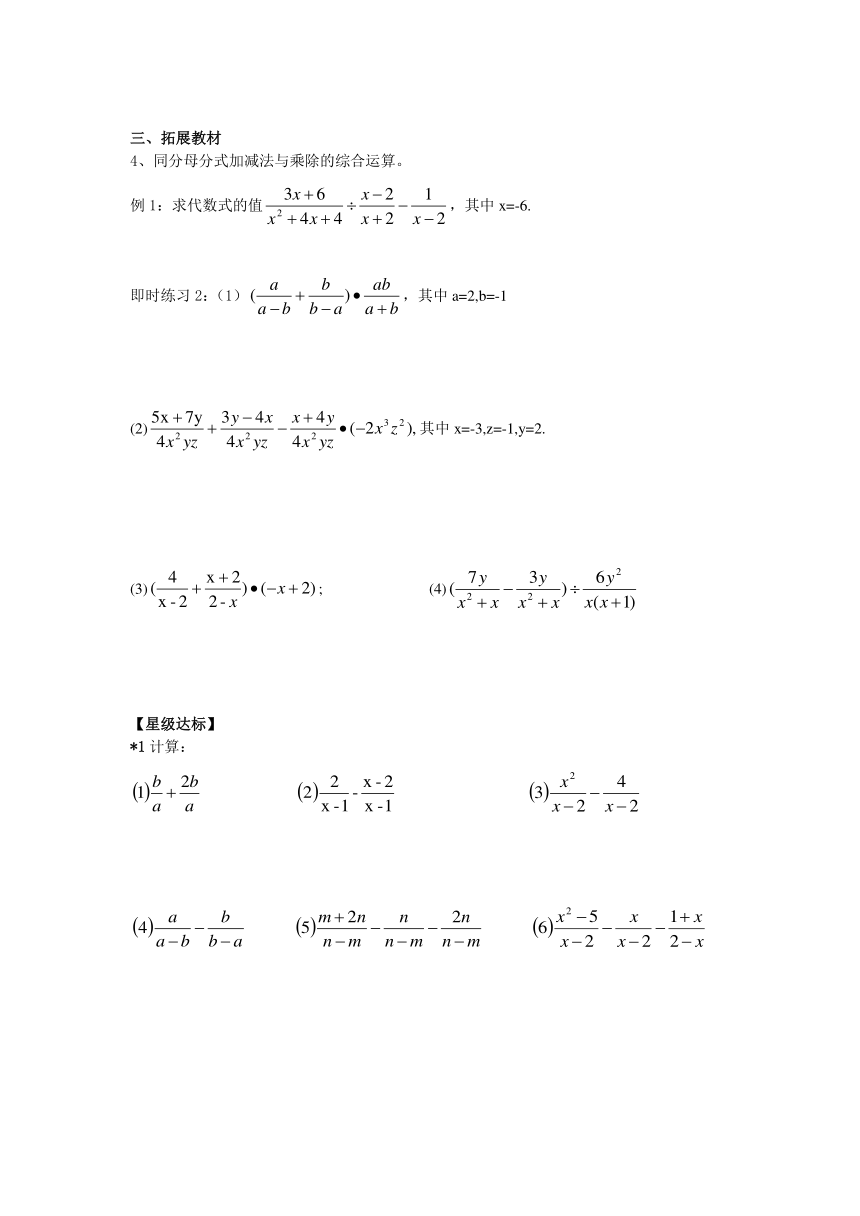
文档简介
第4课时 分式乘除法(自主+精讲)
【学习目标】1、类比分数乘除法的运算法则.探索分式乘除法的运算法则;
2、会进行分式的乘除法的运算;
【学习重点】掌握分式乘除法的法则及其应用。
【学习难点】分子、分母是多项式的分式的乘除法的运算。
【候课朗读】前一节资源链接
【学习过程】
一、学习准备:
阅读教材6—7。
计算
(1)______ (2)(3) (4)
二、解读教材
3.思考:×= ÷= 与同伴交流总结并完成填空:
两个分式相乘,把____________作为积的分子,把_____________作为积的分母,用字母表示_____________;
两个分式相除,把_____________________________后再与____________,用字母表示_________________。
例1计算
(1)·; (2) (3)
解:·(两个分式相乘) 解: 解:
=(分子相乘,分母相乘) =(将除变为乘) =
=(提公因式) = =
= (约分) =
注意:(1)将算式对照乘除法运算法则,进行运算;(2)强调运算结果如不是最简分式时,一定要进行约分,使运算结果化为最简分式.
即时练习1:计算(1) (2) (4)
三、挖掘教材
4.分子分母出现多项式的运算
根据已学可知:×=; ÷=×=.
这里字母a,b,c,d可以代表整式,但a,c,d不为零.
例2、观察书上例题,用分式乘除法法则计算:
(3)
由上题可知:进行分式乘法运算,当分子、分母是多项式时,一般应先分解因式,并在运算过程中约分,使运算简化。
即时练习2:
四、反思小结
1、两个分式相乘(或相除),如果分子和分母都是单项式,可以_________________________________进行计算;如果分子和分母都是多项式,那么先将分子和分母_______________,然后再运用分式的乘法(或除法)法则进行计算。
2、如果整式与分式相乘(或相除),可以把整式看作________________的式子进行计算,当整式是多项式时,同样要先________________。
3、对于,小明是这样计算的:,他的计算过程是正确的吗?为什么?
【星级达标】
*计算下列各式:
【资源连接】巧算对称式
已知a2+3a+1=0,求
(1)a+; (2)a2+; (3)a3+; (4)a4+
第5课时 同分母的分式加减法(自主+精讲)
【学习目标】 1、经历探索同分母分式加减运算法则过程,不断与分数情形类比加深对新知识的理解。
2、能熟练进行同分母分式相加减。
【学习重点】同分母分式加减法
【候课朗读】上节课反思小结
【学习过程】
一、学习准备:
计算:(1)= (2) =
(3)=
2、处理分子、分母、分式的符号
(1) (2) (3)
(4) (5) =
二、解读教材
3、同分母分式加减法法则:类比同分母分数加减:分母不变, 。
例1:(1) (同分母分式相加) (同分母分式相减)
解:原式 = (分母不变,分式相加) 解:原式 = (分母不变,分式相减)
= =
同分母分式的加减的步骤是:_________________________ ;
即时练习1:(1) (2) (3) (4)
三、拓展教材
4、同分母分式加减法与乘除的综合运算。
例1:求代数式的值,其中x=-6.
即时练习2:(1),其中a=2,b=-1
(2)其中x=-3,z=-1,y=2.
(3); (4)
【星级达标】
*1计算:
**2、若
,求M的值。
第6课时 最简公分母和通分(精讲+探究)
【学习目标】1、理解最简公分母和通分的意义。
2、会确定各分母是单项式的分式的最简公分母,会正确进行各分母是单项式的分式的通分。
3、会进行各分母是单项式的异分母的分式的加减。
【学习重点】理解和确定最简公分母。
【候课朗读】6页数式通性。
【学习过程】
一、学习准备
1、填空:同分母分式的加减法法则是 。
2、计算:(1) (2)
二、解读教材
3、分数的最简公分母,求、、的最简公分母。
例:∵ , ,
∴ ,,的最简公分母是8
4、最简公分母的定义: 。
(
分式公分母的确定:1找系数的最小公倍数;2所有字母或多项式都要,且相同的字母或多项式取最高次。
) 分式的最简公分母:求和 的最简公分母。
因为: ①2和3的最小公倍数是6;
②所有的字母有a、b、c,a、b、c的最高次分别是2、3、1;
所以: 和的最简公分母为。
即时训练1:指出下列各式的最简公分母:
(1),; (2); (3) 。
5、分式的通分:
例:通分:,
解: ∵和 的最简公分母是
∴ ,
小结(1)最简公分母:
(2)通分:
(3)通分的关键是:
即时练习2:通分:(1), (2),
三、拓展教材
6、计算的值。
7、分母为单项式的异分母分式加减:
即时练习3:(1) (2)+ (3)
【星级达标】
8、找出最简公分母
*(1)的最简公分母是 ; **(2)的最简公分母是 ;
***(3)的最简公分母是 ;
****(4)通分:
9、异分母分式加减:
*(1) **(2) ***(3)
****(4)
第7课时 异分母分式的加减(自主+探究)
【学习目标】1、能正确的确定几个异分母分式的最简公分母
2、会正确进行异分母分式的加减
【学习重点】确定异分母分式的最简公分母
【学习难点】异分母分式的加减
【学习过程】
一、复习准备
1、找最简公分母的三要素:①系数: ;②因式: ;
③指数: 。
2、计算:① + = ;
② + = 。
3、异分母分式的加减法则: 。
二、解读教材
例1、通分 与
解:∵与的最简公分母是
∴= = =
即时练习1:通分 (1) 与 (2)与
(3)与 (4)与
例2、计算:+
解:+=+
= =
即时练习2:计算:(1) + - (3) -
三、拓展与提升
例3:
解:原式=
例4:用两种方法计算
方法一: 方法二:
用两种方法计算:
【星级达标】(*要求每位学生必须达标)
*1、计算:
2、计算:*(1) *(2)
** (3)
【学习目标】1、类比分数乘除法的运算法则.探索分式乘除法的运算法则;
2、会进行分式的乘除法的运算;
【学习重点】掌握分式乘除法的法则及其应用。
【学习难点】分子、分母是多项式的分式的乘除法的运算。
【候课朗读】前一节资源链接
【学习过程】
一、学习准备:
阅读教材6—7。
计算
(1)______ (2)(3) (4)
二、解读教材
3.思考:×= ÷= 与同伴交流总结并完成填空:
两个分式相乘,把____________作为积的分子,把_____________作为积的分母,用字母表示_____________;
两个分式相除,把_____________________________后再与____________,用字母表示_________________。
例1计算
(1)·; (2) (3)
解:·(两个分式相乘) 解: 解:
=(分子相乘,分母相乘) =(将除变为乘) =
=(提公因式) = =
= (约分) =
注意:(1)将算式对照乘除法运算法则,进行运算;(2)强调运算结果如不是最简分式时,一定要进行约分,使运算结果化为最简分式.
即时练习1:计算(1) (2) (4)
三、挖掘教材
4.分子分母出现多项式的运算
根据已学可知:×=; ÷=×=.
这里字母a,b,c,d可以代表整式,但a,c,d不为零.
例2、观察书上例题,用分式乘除法法则计算:
(3)
由上题可知:进行分式乘法运算,当分子、分母是多项式时,一般应先分解因式,并在运算过程中约分,使运算简化。
即时练习2:
四、反思小结
1、两个分式相乘(或相除),如果分子和分母都是单项式,可以_________________________________进行计算;如果分子和分母都是多项式,那么先将分子和分母_______________,然后再运用分式的乘法(或除法)法则进行计算。
2、如果整式与分式相乘(或相除),可以把整式看作________________的式子进行计算,当整式是多项式时,同样要先________________。
3、对于,小明是这样计算的:,他的计算过程是正确的吗?为什么?
【星级达标】
*计算下列各式:
【资源连接】巧算对称式
已知a2+3a+1=0,求
(1)a+; (2)a2+; (3)a3+; (4)a4+
第5课时 同分母的分式加减法(自主+精讲)
【学习目标】 1、经历探索同分母分式加减运算法则过程,不断与分数情形类比加深对新知识的理解。
2、能熟练进行同分母分式相加减。
【学习重点】同分母分式加减法
【候课朗读】上节课反思小结
【学习过程】
一、学习准备:
计算:(1)= (2) =
(3)=
2、处理分子、分母、分式的符号
(1) (2) (3)
(4) (5) =
二、解读教材
3、同分母分式加减法法则:类比同分母分数加减:分母不变, 。
例1:(1) (同分母分式相加) (同分母分式相减)
解:原式 = (分母不变,分式相加) 解:原式 = (分母不变,分式相减)
= =
同分母分式的加减的步骤是:_________________________ ;
即时练习1:(1) (2) (3) (4)
三、拓展教材
4、同分母分式加减法与乘除的综合运算。
例1:求代数式的值,其中x=-6.
即时练习2:(1),其中a=2,b=-1
(2)其中x=-3,z=-1,y=2.
(3); (4)
【星级达标】
*1计算:
**2、若
,求M的值。
第6课时 最简公分母和通分(精讲+探究)
【学习目标】1、理解最简公分母和通分的意义。
2、会确定各分母是单项式的分式的最简公分母,会正确进行各分母是单项式的分式的通分。
3、会进行各分母是单项式的异分母的分式的加减。
【学习重点】理解和确定最简公分母。
【候课朗读】6页数式通性。
【学习过程】
一、学习准备
1、填空:同分母分式的加减法法则是 。
2、计算:(1) (2)
二、解读教材
3、分数的最简公分母,求、、的最简公分母。
例:∵ , ,
∴ ,,的最简公分母是8
4、最简公分母的定义: 。
(
分式公分母的确定:1找系数的最小公倍数;2所有字母或多项式都要,且相同的字母或多项式取最高次。
) 分式的最简公分母:求和 的最简公分母。
因为: ①2和3的最小公倍数是6;
②所有的字母有a、b、c,a、b、c的最高次分别是2、3、1;
所以: 和的最简公分母为。
即时训练1:指出下列各式的最简公分母:
(1),; (2); (3) 。
5、分式的通分:
例:通分:,
解: ∵和 的最简公分母是
∴ ,
小结(1)最简公分母:
(2)通分:
(3)通分的关键是:
即时练习2:通分:(1), (2),
三、拓展教材
6、计算的值。
7、分母为单项式的异分母分式加减:
即时练习3:(1) (2)+ (3)
【星级达标】
8、找出最简公分母
*(1)的最简公分母是 ; **(2)的最简公分母是 ;
***(3)的最简公分母是 ;
****(4)通分:
9、异分母分式加减:
*(1) **(2) ***(3)
****(4)
第7课时 异分母分式的加减(自主+探究)
【学习目标】1、能正确的确定几个异分母分式的最简公分母
2、会正确进行异分母分式的加减
【学习重点】确定异分母分式的最简公分母
【学习难点】异分母分式的加减
【学习过程】
一、复习准备
1、找最简公分母的三要素:①系数: ;②因式: ;
③指数: 。
2、计算:① + = ;
② + = 。
3、异分母分式的加减法则: 。
二、解读教材
例1、通分 与
解:∵与的最简公分母是
∴= = =
即时练习1:通分 (1) 与 (2)与
(3)与 (4)与
例2、计算:+
解:+=+
= =
即时练习2:计算:(1) + - (3) -
三、拓展与提升
例3:
解:原式=
例4:用两种方法计算
方法一: 方法二:
用两种方法计算:
【星级达标】(*要求每位学生必须达标)
*1、计算:
2、计算:*(1) *(2)
** (3)
