九年级上册数学期末试题
图片预览

文档简介
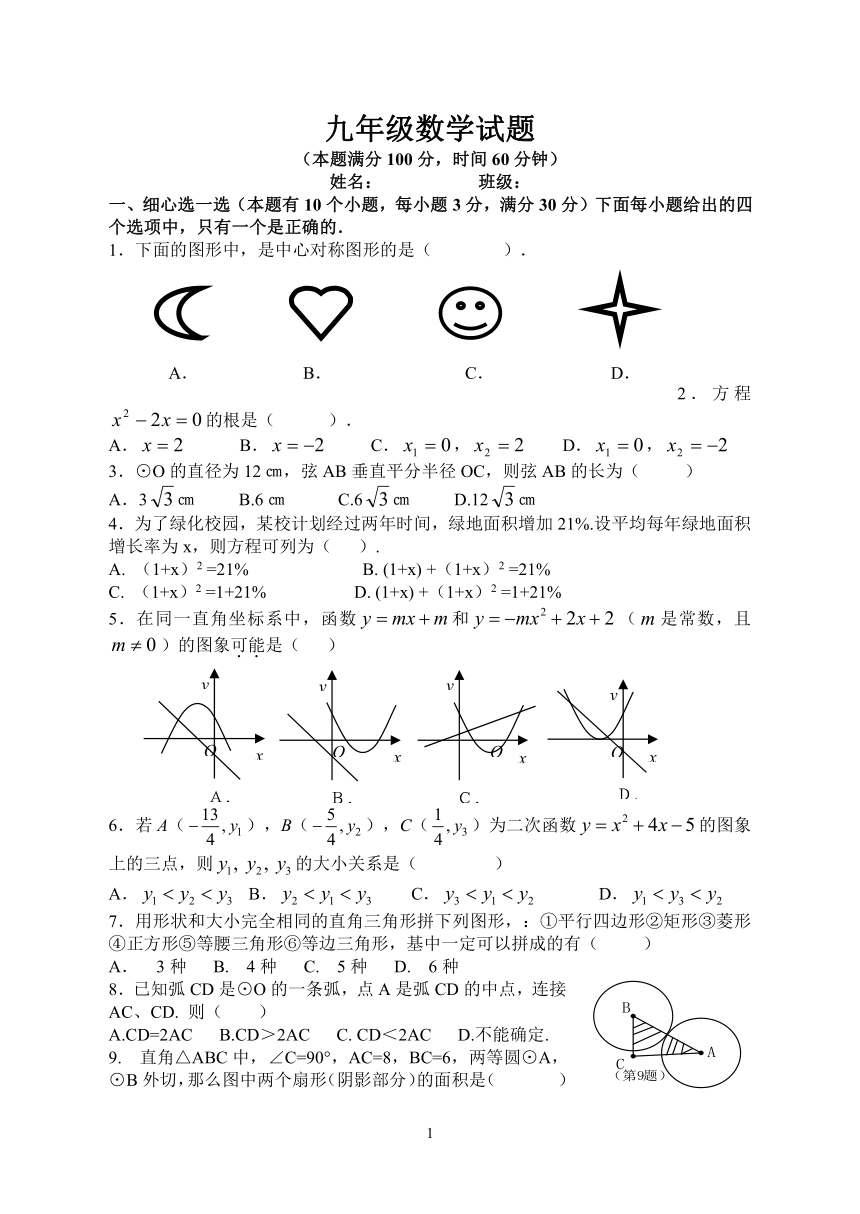
九年级数学试题
(本题满分100分,时间60分钟)
姓名: 班级:
一、细心选一选(本题有10个小题,每小题3分,满分30分)下面每小题给出的四个选项中,只有一个是正确的.
1.下面的图形中,是中心对称图形的是( ).
2.方程的根是( ).
A. B. C., D.,
3.⊙O的直径为12㎝,弦AB垂直平分半径OC,则弦AB的长为( )
A.3㎝ B.6㎝ C.6㎝ D.12㎝
4.为了绿化校园,某校计划经过两年时间,绿地面积增加21%.设平均每年绿地面积增长率为x,则方程可列为( ).
A. (1+x)2 =21% B. (1+x) +(1+x)2 =21%
C. (1+x)2 =1+21% D. (1+x) +(1+x)2 =1+21%
5.在同一直角坐标系中,函数和(是常数,且)的图象可能是( )
6.若A( HYPERLINK "http:///" ),B(),C()为二次函数的图象上的三点,则的大小关系是( )
A. B. C. D.
7.用形状和大小完全相同的直角三角形拼下列图形,:①平行四边形②矩形③菱形④正方形⑤等腰三角形⑥等边三角形,基中一定可以拼成的有( )
A. 3种 B. 4种 C. 5种 D. 6种
8.已知弧CD是⊙O的一条弧,点A是弧CD的中点,连接AC、CD. 则( )
A.CD=2AC B.CD>2AC C. CD<2AC D.不能确定.
9. 直角△ABC中,∠C=90°,AC=8,BC=6,两等圆⊙A,⊙B外切,那么图中两个扇形(阴影部分)的面积是( )
A. B. C. D.
10.把抛物线向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )
A. B. C. D.
二、耐心填一填(本题有8个小题,每小题3分,共24分).
11.已知两圆相切,圆心距为8㎝,如果一圆的半径是5㎝,则另一圆的半径是 ㎝。
12.如果关于x的一元二次方程k2x2+kx=0的一个根是-2,那么k= .
13.在直角三角形中,若两条直角边长分别为6cm和8cm,则三角形的内切圆半径与外接圆半径之比为 .
14.依次连接等腰梯形各边中点所得到的四边形是 .
15.⊿ABC中,D、E、F分别为AB、BC、AC的中点,过点A作AH⊥BC于点H,连接DE、DF、HF,若DE=6,则FH= .
16.抛物线与轴只有一个公共点,则的值为 .
17.如图,AB是⊙O的直径,AB=10㎝,M是半圆AB的一个三等分点,N是半圆AB的一个六等分点,P是直径AB上一动点,连结MP、NP,则MP+NP的最小值是 ㎝.
18.如果一个平行四边形的边长是8,一条对角线为6,那么它的另一条对角线的长a的取值范围是 .
19.(本题满分8分)
已知二次函数
(1)当实数k为何值时,图象经过原点?
(2)当实数k为何值时,图象顶点在y轴?
(3)当实数k在何范围取值时,函数顶点在x轴下方?
(4)当实数k在何范围取值时,函数顶点在第四象限内?
20.解下列一元二次方程. (本题满分8分)
⑴.2x2+5x=3 ⑵.(x-2)(2x-1)=1-2x
21.(本题满分10分)如图:在⊿ABC中,∠BAC90°,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E,EF⊥BC于F.求证:四边形AEFG是菱形;
22.(本题满分10分)已知:如图,AB是⊙O的直径,C是⊙O上一点,CD切⊙O于点C,AD⊥CD,垂足为D,延长AD和BC的延长线交于点E,求证:AB=AE.
23.(本题满分10分)已知二次函数的图象以A(-1,4)为顶点,且过点B(2,-5)
①求该函数的关系式;
②求该函数图象与坐标轴的交点坐标;
③将该函数图象向右平移,当图象经过原点时,A、B两点随图象移至A′、B′,求△O A′B′的面积.
A.
B.
C.
D.
x
y
O
A.
x
y
O
B.
x
y
O
C.
x
y
O
D.
PAGE
4
(本题满分100分,时间60分钟)
姓名: 班级:
一、细心选一选(本题有10个小题,每小题3分,满分30分)下面每小题给出的四个选项中,只有一个是正确的.
1.下面的图形中,是中心对称图形的是( ).
2.方程的根是( ).
A. B. C., D.,
3.⊙O的直径为12㎝,弦AB垂直平分半径OC,则弦AB的长为( )
A.3㎝ B.6㎝ C.6㎝ D.12㎝
4.为了绿化校园,某校计划经过两年时间,绿地面积增加21%.设平均每年绿地面积增长率为x,则方程可列为( ).
A. (1+x)2 =21% B. (1+x) +(1+x)2 =21%
C. (1+x)2 =1+21% D. (1+x) +(1+x)2 =1+21%
5.在同一直角坐标系中,函数和(是常数,且)的图象可能是( )
6.若A( HYPERLINK "http:///" ),B(),C()为二次函数的图象上的三点,则的大小关系是( )
A. B. C. D.
7.用形状和大小完全相同的直角三角形拼下列图形,:①平行四边形②矩形③菱形④正方形⑤等腰三角形⑥等边三角形,基中一定可以拼成的有( )
A. 3种 B. 4种 C. 5种 D. 6种
8.已知弧CD是⊙O的一条弧,点A是弧CD的中点,连接AC、CD. 则( )
A.CD=2AC B.CD>2AC C. CD<2AC D.不能确定.
9. 直角△ABC中,∠C=90°,AC=8,BC=6,两等圆⊙A,⊙B外切,那么图中两个扇形(阴影部分)的面积是( )
A. B. C. D.
10.把抛物线向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )
A. B. C. D.
二、耐心填一填(本题有8个小题,每小题3分,共24分).
11.已知两圆相切,圆心距为8㎝,如果一圆的半径是5㎝,则另一圆的半径是 ㎝。
12.如果关于x的一元二次方程k2x2+kx=0的一个根是-2,那么k= .
13.在直角三角形中,若两条直角边长分别为6cm和8cm,则三角形的内切圆半径与外接圆半径之比为 .
14.依次连接等腰梯形各边中点所得到的四边形是 .
15.⊿ABC中,D、E、F分别为AB、BC、AC的中点,过点A作AH⊥BC于点H,连接DE、DF、HF,若DE=6,则FH= .
16.抛物线与轴只有一个公共点,则的值为 .
17.如图,AB是⊙O的直径,AB=10㎝,M是半圆AB的一个三等分点,N是半圆AB的一个六等分点,P是直径AB上一动点,连结MP、NP,则MP+NP的最小值是 ㎝.
18.如果一个平行四边形的边长是8,一条对角线为6,那么它的另一条对角线的长a的取值范围是 .
19.(本题满分8分)
已知二次函数
(1)当实数k为何值时,图象经过原点?
(2)当实数k为何值时,图象顶点在y轴?
(3)当实数k在何范围取值时,函数顶点在x轴下方?
(4)当实数k在何范围取值时,函数顶点在第四象限内?
20.解下列一元二次方程. (本题满分8分)
⑴.2x2+5x=3 ⑵.(x-2)(2x-1)=1-2x
21.(本题满分10分)如图:在⊿ABC中,∠BAC90°,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E,EF⊥BC于F.求证:四边形AEFG是菱形;
22.(本题满分10分)已知:如图,AB是⊙O的直径,C是⊙O上一点,CD切⊙O于点C,AD⊥CD,垂足为D,延长AD和BC的延长线交于点E,求证:AB=AE.
23.(本题满分10分)已知二次函数的图象以A(-1,4)为顶点,且过点B(2,-5)
①求该函数的关系式;
②求该函数图象与坐标轴的交点坐标;
③将该函数图象向右平移,当图象经过原点时,A、B两点随图象移至A′、B′,求△O A′B′的面积.
A.
B.
C.
D.
x
y
O
A.
x
y
O
B.
x
y
O
C.
x
y
O
D.
PAGE
4
同课章节目录
