小学数学西师大版六年级下 总复习 统计与概率(1) 课件(43页PPT)
文档属性
| 名称 | 小学数学西师大版六年级下 总复习 统计与概率(1) 课件(43页PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-04 10:45:07 | ||
图片预览








文档简介
大家回忆一下,我们学习过哪些统计知识。你会做一项调查统计并进行数据分析吗?
统计
数据的收集和整理
统计表
统计图
单式统计表
复式统计表
条形统计图(单式和复式)
折线统计图(单式和复式)
扇形统计图
统计量
平均数
中位数
众数
数据的收集和整理:
在收集数据时,通常采用画“正”字的方法比较简便。这样得到的数据叫做原始数据。
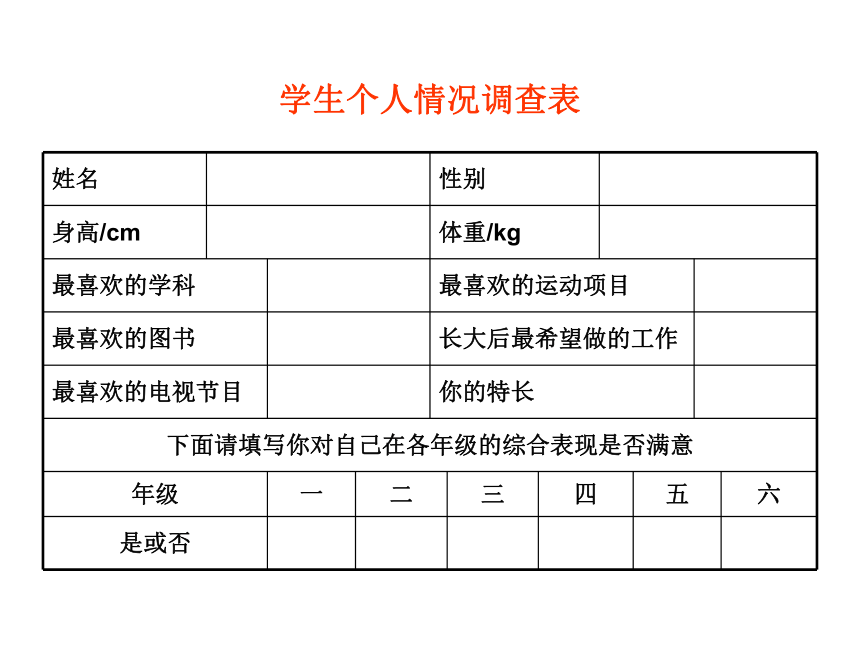
学生个人情况调查表
姓名
性别
身高/cm
体重/kg
最喜欢的学科
最喜欢的运动项目
最喜欢的图书
长大后最希望做的工作
最喜欢的电视节目
你的特长
下面请填写你对自己在各年级的综合表现是否满意
年级
一
二
三
四
五
六
是或否
统计表:
把收集到的数据经过分类、整理后,填在一定格式的表格内,用来反映情况,说明问题,这种表格叫做统计表。
统计表一般分为单式统计表和复式统计表。
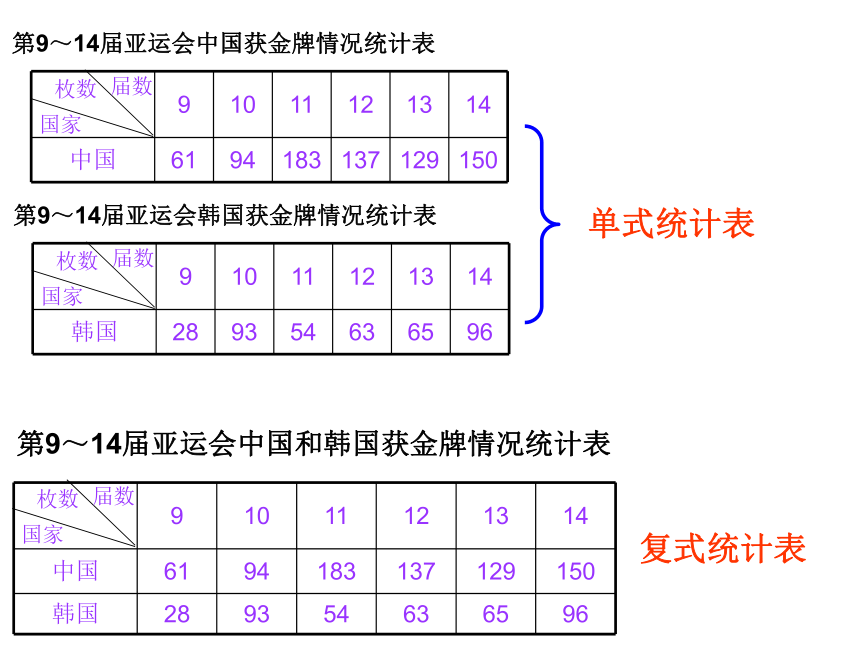
第9~14届亚运会中国和韩国获金牌情况统计表
9
10
11
12
13
14
中国
61
94
183
137
129
150
韩国
28
93
54
63
65
96
届数
枚数
国家
第9~14届亚运会中国获金牌情况统计表
9
10
11
12
13
14
中国
61
94
183
137
129
150
届数
枚数
国家
第9~14届亚运会韩国获金牌情况统计表
9
10
11
12
13
14
韩国
28
93
54
63
65
96
届数
枚数
国家
单式统计表
复式统计表
性别
男生
女生
合计
人数
22
18
40
六(1)班男、女生人数统计表
足球
跳绳
乒乓球
其他
男生
12
2
5
3
女生
3
6
5
4
六(1)班同学最喜欢的运动项目统计表
六(1)班同学对自己的综合表现满意人数的情况统计表
年级
一
二
三
四
五
六
满意人数
30
32
31
30
33
35
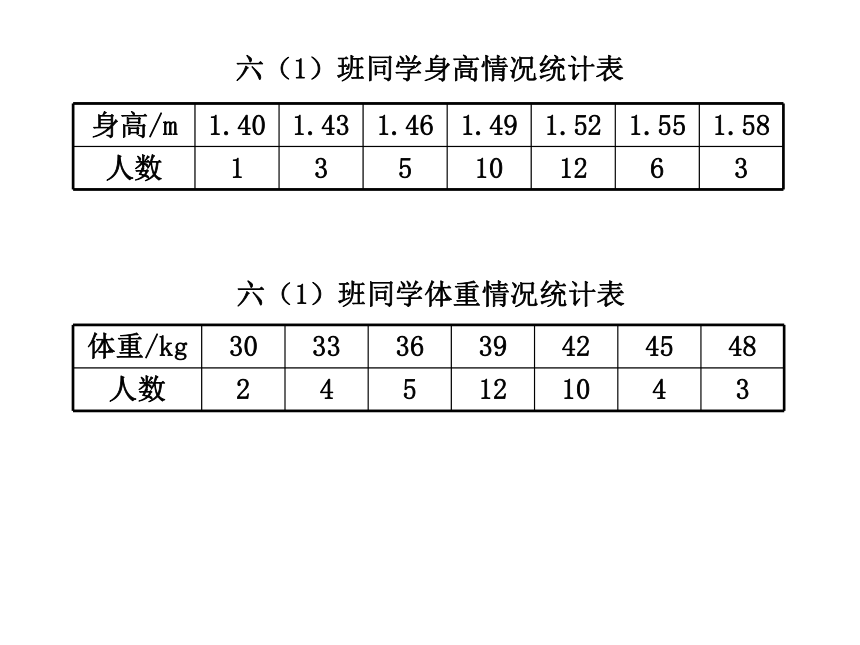
六(1)班同学身高情况统计表
身高/m
1.40
1.43
1.46
1.49
1.52
1.55
1.58
人数
1
3
5
10
12
6
3
体重/kg
30
33
36
39
42
45
48
人数
2
4
5
12
10
4
3
六(1)班同学体重情况统计表
统计图:
常见的统计图有 、 、
。
其中 统计图表示数量的多少; 统计图不仅可以表示数量的多少,还可以反映数量的增减变化; 统计图仅表示部分和总数的关系。
条形统计图
折线统计图
扇形统计图
条形
折线
扇形
条形统计图
折线统计图
扇形统计图
特点
作用
三种统计图的特点和作用对比
用一个单位长度表示一定的数量
用整个圆面积表示总数,用扇形面积表示各部分占总数的百分数。
用直条的长短表示数量的多少。
用折线的起伏表示数量的增减变化。
能清楚地看出各数量的多少,便于相互比较。
能清楚地看出数量增减变化的情况,也能看出数量的多少。
能清楚地看出各部分与总数的百分比,以及部分与部分之间的关系。
统计与概率
第2课时
性别
男生
女生
合计
人数
22
18
40
六(1)班男、女生人数统计表
如果要反映六(1)班男、女生人数占全班人数的百分比,应选用什么统计图合适?
根据以上统计表和统计图,你得到了哪些信息?
足球
跳绳
乒乓球
其他
男生
12
2
5
3
女生
3
6
5
4
六(1)班同学最喜欢的运动项目统计表
用什么统计图来反映六(1)班同学最喜欢的运动项目呢?
根据以上统计表和统计图,你得到了哪些信息?
人数/人
项目
足球
跳绳
乒乓球
其他
5
10
12
3
2
6
5
5
3
4
0
男
女
六(1)班同学最喜欢的运动项目统计图
六(1)班同学对自己的综合表现满意人数的情况统计表
年级
一
二
三
四
五
六
满意人数
30
32
31
30
33
35
要反映六(1)班同学对自己在各年级的综合表现满意人数的变化趋势,用什么统计图?
根据以上统计表和统计图,你得到了哪些信息?
年级
人数/人
0
一
二
三
四
五
六
5
10
15
20
25
30
35
40
30
32
31
30
33
35
六(1)班同学对自己的综合表现满意人数的情况统计图
做好一项调查统计工作的主要步骤有哪些?
1、确定调查的主题及需要调查的数据。
2、根据调查的主题和数据设计调查表(用于问卷调查)或统计表(用于收集现成数据)。
3、确定调查的方法。是实地调查、测量,还是问卷调查,或是收集各种媒体上的信息。
4、进行调查,收集数据。把数据记录在调查表上或统计表上。
5、整理和描述数据。对数据进行分类,选择适当的统计图或统计表表示数据。
6、根据统计图或统计表分析数据,作出判断和结论。
统计与概率
第3课时
(1)在上面两组数据中,平均数、中位数和众数各是什么?
身高:
平均数:(1.4+1.43×3+1.46×5+1.49×10+1.52×12+1.55×6+1.58×3) ÷40
=60.17 ÷40
≈1.50(m)
体重:
平均数:(30×2+33×4+36×5+39×12+42×10+45×4+48×3) ÷40
=1584 ÷40
=39.6(kg)
中位数:就是第20、21名之间的身高。所以中位数是1.52。
众数:1.52。
中位数:就是第20、21名之间的体重。所以中位数是39。
众数:39。
六(1)班同学身高、体重情况统计表
身高/m
1.40
1.43
1.46
1.49
1.52
1.55
1.58
人数
1
3
5
10
12
6
3
体重/kg
30
33
36
39
42
45
48
人数
2
4
5
12
10
4
3
5
(2)答:平均数有时比众数大。有时比众数小。
(3)答:用平均数表示比较合适。因为它与这组数据中的每个数据都有关系。
统计量:
1、平均数
一组数据的和除以这组数据的个数所得的商叫做这组数据的平均数。一组数据只有一个平均数。
求平均数的方法:数据总和÷数据个数=平均数。
用平均数作为一组数据的代表,比较可靠和稳定,但它容易受到极端数据(偏大或偏小的数据)的影响。
统计量:
2、中位数
把一组数据按大小顺序排列,位于中间位置的一个数据(或中间位置的两个数据的平均数)叫做这组数据的中位数。一组数据只有一个中位数。
求中位数的方法:先把数据从小到大(或从大到小)的顺序排列。如果数据的个数是奇数,正中间的那个数据就是这组数据的中位数。如果数据的个数是偶数,正中间两个数据的平均数就是这组数据的中位数。
用中位数作为一组数据的代表,可靠性比较差,但中位数不受极端数据(偏大或偏小的数据)的影响,当一组数据中个别数据变化较大时,选择中位数来表示这组数据的集中趋势比较合适。
统计量:
3、众数
一组数据中出现次数最多的数据叫做这组数据的众数。一组数据的众数可能只有一个,也可能不止一个,也可能没有。
求众数的方法:先统计一组数据中每个数据出现的次数,再找出出现次数最多的数据就是这组数据的众数。
用众数作为一组数据的代表,可靠性比较差,但它不受极端数据(偏大或偏小的数据)的影响,并且求法简便。当一组数据中个别数据变化较大时,适宜选择众数来表示这组数据的集中趋势。
学校举办英语百词听写竞赛,五(1)班和五(2)班参赛选手的成绩如下:
五(1)班:88 87 88 87 85 96 98 90 87 91 93
99 87 95 88 92 94 88 87 88
五(2)班:82 96 87 89 94 95 83 96 92 84 93
97 85 98 99 88 91 90 81 80
这组数据的众数各是多少?你发现了什么?
五(1)班:87和88,五(2)班没有
在一组数据中,众数可能不止一个,也可能没有众数。
平均数、中位数和众数的数量和意义
平均数
中位数
众数
数量
意义
一个
一个(奇、偶有别)
一个、多个
或没有
数据的
平均水平
数据的
中间水平
数据的
集中水平
众数它代表了一组数据中出现次数最多的数据。但它只能传递这组数据中的很少一部分信息。
中位数很好地代表了一组数据的中点,并且需要较少的计算。中位数对极端数据不敏感,在某些情况下是一个优点。但除了中间值,中位数没有利用其他数据。
平均数将所有的数据都加以利用。与中位数和众数相比,它会包括更多的信息。因此,平均数是刻画一组数据集中趋势的最常用的统计量,当平均数与中位数大致相当时,人们往往选择平均数。但它计算起来有点麻烦,同时易受极端数据的影响。
以上三个统计量各有优势,在实际问题中需要选择合适的统计量去刻画数据的集中趋势。有时,需要灵活加以运用。
统计与概率
第4课时
(1)该公司去年全年总体经营情况很好,产量和销量不断增长,第四季度增长幅度较快,而且出现了销量大于产量的良好势头。
(2)该公司在未来的一段时间内将有良好的发展。
因为平均数它与一组数据中的每个数据都有关系,它易受极端数据的影响,所以为了减少这种影响,在评分时就采取去掉一个最高分和一个最低分,再计算平均数,这样做是合理的。
可能性的概念:
可能性是指事物发生的概率。是包含在事物之中并预示着实物发展趋势的量化指标。
数学中的可能性:
必然事件:100%。即一定会发生的事件。如:今天
是星期一,明天一定是星期二。
不确定事件:x%。即在主观或客观条件下都不能确定
是否会发生的事件,常用“不一定”、“经
常”、“可能”、“偶尔”等词语来描述。
如:今天下雨,明天不一定也要下雨。
不可能事件:0%。即在逻辑思维下不会发生的事件。
如:太阳不可能从西边升起。
在我们这个世界中,可能性不会超过1(100%)。
游戏的公平性:
(1)玩游戏时,游戏规则必须保证事件发生的可能性相同,这样游戏才公平。确定一个游戏是否公平,要先找出事件发生的所有可能,然后看对于游戏双方发生的可能性是否相同。若相同,游戏公平,如果不相同,游戏就不公平。
(2)判断一个游戏的公平性,关键是看参加游戏的各方获胜的机会是否均等。
(3)设计公平的游戏方案,应考虑两个方面:一是要让可能出现的结果是有限的;二是出现各种结果的可能性相等。
用几分之几来描述一个事件发生的可能性:
求一事件发生的可能性,要先找出这一事件所有可能出现的结果(假设有b种可能的结果),再找出所求事件发生的可能结果(假设有a种结果),那么这一事件发生的可能性就是 。
如:盒子里有2个白球、3个红球和4个绿球,摸到白球的可能性是 。
课
堂
习
练
第5课时
1、任意从装有10枚白子和12枚黑子的袋子里摸出1枚子,那么摸到(? )的可能性大,摸到( )的可能性小。
2、在下面的括号里填“一定”、“可能”、或“不可能”。
明天( )会下雨。
太阳( )从东边落下。
哈尔滨的冬天( )会下雪。
这次测验我( )会得100分。
3、从一副除去大、小王的扑克牌中任意抽取一张是5的概率为( )。???
黑子
白子
可能
不可能
一定
可能
4、某地的天气预报中说:“明天的降水率是80%。”根据这个预报,判断下面的说法是否正确。(正确的“√”,错误的“×”)
(1)明天一定下雨(?? )?????
(2)明天下雨的可能性很小(?? )
(3)明天不可能下雨(?? )???
(4)明天下雨的可能性很大(?? )
×
×
×
√
5、用1、2、3组成三位数,出现单数的可能性是 ;出现双数的可能性是 。
6、用2、3、4组成三位数,出现单数的可能性是 ;出现双数的可能性是 。
7、用1、2、3、4组成三位数,出现单数的可能性是 ;出现双数的可能性是 。
8、桌子上摆着9张卡片,分别写着1-9各数。如果摸到单数小明赢,如果摸到双数小红赢。
(1)这个游戏公平吗?
(2)小红一定会输吗?
(3)你能设计一个公平的规则吗?
统计
数据的收集和整理
统计表
统计图
单式统计表
复式统计表
条形统计图(单式和复式)
折线统计图(单式和复式)
扇形统计图
统计量
平均数
中位数
众数
数据的收集和整理:
在收集数据时,通常采用画“正”字的方法比较简便。这样得到的数据叫做原始数据。
学生个人情况调查表
姓名
性别
身高/cm
体重/kg
最喜欢的学科
最喜欢的运动项目
最喜欢的图书
长大后最希望做的工作
最喜欢的电视节目
你的特长
下面请填写你对自己在各年级的综合表现是否满意
年级
一
二
三
四
五
六
是或否
统计表:
把收集到的数据经过分类、整理后,填在一定格式的表格内,用来反映情况,说明问题,这种表格叫做统计表。
统计表一般分为单式统计表和复式统计表。
第9~14届亚运会中国和韩国获金牌情况统计表
9
10
11
12
13
14
中国
61
94
183
137
129
150
韩国
28
93
54
63
65
96
届数
枚数
国家
第9~14届亚运会中国获金牌情况统计表
9
10
11
12
13
14
中国
61
94
183
137
129
150
届数
枚数
国家
第9~14届亚运会韩国获金牌情况统计表
9
10
11
12
13
14
韩国
28
93
54
63
65
96
届数
枚数
国家
单式统计表
复式统计表
性别
男生
女生
合计
人数
22
18
40
六(1)班男、女生人数统计表
足球
跳绳
乒乓球
其他
男生
12
2
5
3
女生
3
6
5
4
六(1)班同学最喜欢的运动项目统计表
六(1)班同学对自己的综合表现满意人数的情况统计表
年级
一
二
三
四
五
六
满意人数
30
32
31
30
33
35
六(1)班同学身高情况统计表
身高/m
1.40
1.43
1.46
1.49
1.52
1.55
1.58
人数
1
3
5
10
12
6
3
体重/kg
30
33
36
39
42
45
48
人数
2
4
5
12
10
4
3
六(1)班同学体重情况统计表
统计图:
常见的统计图有 、 、
。
其中 统计图表示数量的多少; 统计图不仅可以表示数量的多少,还可以反映数量的增减变化; 统计图仅表示部分和总数的关系。
条形统计图
折线统计图
扇形统计图
条形
折线
扇形
条形统计图
折线统计图
扇形统计图
特点
作用
三种统计图的特点和作用对比
用一个单位长度表示一定的数量
用整个圆面积表示总数,用扇形面积表示各部分占总数的百分数。
用直条的长短表示数量的多少。
用折线的起伏表示数量的增减变化。
能清楚地看出各数量的多少,便于相互比较。
能清楚地看出数量增减变化的情况,也能看出数量的多少。
能清楚地看出各部分与总数的百分比,以及部分与部分之间的关系。
统计与概率
第2课时
性别
男生
女生
合计
人数
22
18
40
六(1)班男、女生人数统计表
如果要反映六(1)班男、女生人数占全班人数的百分比,应选用什么统计图合适?
根据以上统计表和统计图,你得到了哪些信息?
足球
跳绳
乒乓球
其他
男生
12
2
5
3
女生
3
6
5
4
六(1)班同学最喜欢的运动项目统计表
用什么统计图来反映六(1)班同学最喜欢的运动项目呢?
根据以上统计表和统计图,你得到了哪些信息?
人数/人
项目
足球
跳绳
乒乓球
其他
5
10
12
3
2
6
5
5
3
4
0
男
女
六(1)班同学最喜欢的运动项目统计图
六(1)班同学对自己的综合表现满意人数的情况统计表
年级
一
二
三
四
五
六
满意人数
30
32
31
30
33
35
要反映六(1)班同学对自己在各年级的综合表现满意人数的变化趋势,用什么统计图?
根据以上统计表和统计图,你得到了哪些信息?
年级
人数/人
0
一
二
三
四
五
六
5
10
15
20
25
30
35
40
30
32
31
30
33
35
六(1)班同学对自己的综合表现满意人数的情况统计图
做好一项调查统计工作的主要步骤有哪些?
1、确定调查的主题及需要调查的数据。
2、根据调查的主题和数据设计调查表(用于问卷调查)或统计表(用于收集现成数据)。
3、确定调查的方法。是实地调查、测量,还是问卷调查,或是收集各种媒体上的信息。
4、进行调查,收集数据。把数据记录在调查表上或统计表上。
5、整理和描述数据。对数据进行分类,选择适当的统计图或统计表表示数据。
6、根据统计图或统计表分析数据,作出判断和结论。
统计与概率
第3课时
(1)在上面两组数据中,平均数、中位数和众数各是什么?
身高:
平均数:(1.4+1.43×3+1.46×5+1.49×10+1.52×12+1.55×6+1.58×3) ÷40
=60.17 ÷40
≈1.50(m)
体重:
平均数:(30×2+33×4+36×5+39×12+42×10+45×4+48×3) ÷40
=1584 ÷40
=39.6(kg)
中位数:就是第20、21名之间的身高。所以中位数是1.52。
众数:1.52。
中位数:就是第20、21名之间的体重。所以中位数是39。
众数:39。
六(1)班同学身高、体重情况统计表
身高/m
1.40
1.43
1.46
1.49
1.52
1.55
1.58
人数
1
3
5
10
12
6
3
体重/kg
30
33
36
39
42
45
48
人数
2
4
5
12
10
4
3
5
(2)答:平均数有时比众数大。有时比众数小。
(3)答:用平均数表示比较合适。因为它与这组数据中的每个数据都有关系。
统计量:
1、平均数
一组数据的和除以这组数据的个数所得的商叫做这组数据的平均数。一组数据只有一个平均数。
求平均数的方法:数据总和÷数据个数=平均数。
用平均数作为一组数据的代表,比较可靠和稳定,但它容易受到极端数据(偏大或偏小的数据)的影响。
统计量:
2、中位数
把一组数据按大小顺序排列,位于中间位置的一个数据(或中间位置的两个数据的平均数)叫做这组数据的中位数。一组数据只有一个中位数。
求中位数的方法:先把数据从小到大(或从大到小)的顺序排列。如果数据的个数是奇数,正中间的那个数据就是这组数据的中位数。如果数据的个数是偶数,正中间两个数据的平均数就是这组数据的中位数。
用中位数作为一组数据的代表,可靠性比较差,但中位数不受极端数据(偏大或偏小的数据)的影响,当一组数据中个别数据变化较大时,选择中位数来表示这组数据的集中趋势比较合适。
统计量:
3、众数
一组数据中出现次数最多的数据叫做这组数据的众数。一组数据的众数可能只有一个,也可能不止一个,也可能没有。
求众数的方法:先统计一组数据中每个数据出现的次数,再找出出现次数最多的数据就是这组数据的众数。
用众数作为一组数据的代表,可靠性比较差,但它不受极端数据(偏大或偏小的数据)的影响,并且求法简便。当一组数据中个别数据变化较大时,适宜选择众数来表示这组数据的集中趋势。
学校举办英语百词听写竞赛,五(1)班和五(2)班参赛选手的成绩如下:
五(1)班:88 87 88 87 85 96 98 90 87 91 93
99 87 95 88 92 94 88 87 88
五(2)班:82 96 87 89 94 95 83 96 92 84 93
97 85 98 99 88 91 90 81 80
这组数据的众数各是多少?你发现了什么?
五(1)班:87和88,五(2)班没有
在一组数据中,众数可能不止一个,也可能没有众数。
平均数、中位数和众数的数量和意义
平均数
中位数
众数
数量
意义
一个
一个(奇、偶有别)
一个、多个
或没有
数据的
平均水平
数据的
中间水平
数据的
集中水平
众数它代表了一组数据中出现次数最多的数据。但它只能传递这组数据中的很少一部分信息。
中位数很好地代表了一组数据的中点,并且需要较少的计算。中位数对极端数据不敏感,在某些情况下是一个优点。但除了中间值,中位数没有利用其他数据。
平均数将所有的数据都加以利用。与中位数和众数相比,它会包括更多的信息。因此,平均数是刻画一组数据集中趋势的最常用的统计量,当平均数与中位数大致相当时,人们往往选择平均数。但它计算起来有点麻烦,同时易受极端数据的影响。
以上三个统计量各有优势,在实际问题中需要选择合适的统计量去刻画数据的集中趋势。有时,需要灵活加以运用。
统计与概率
第4课时
(1)该公司去年全年总体经营情况很好,产量和销量不断增长,第四季度增长幅度较快,而且出现了销量大于产量的良好势头。
(2)该公司在未来的一段时间内将有良好的发展。
因为平均数它与一组数据中的每个数据都有关系,它易受极端数据的影响,所以为了减少这种影响,在评分时就采取去掉一个最高分和一个最低分,再计算平均数,这样做是合理的。
可能性的概念:
可能性是指事物发生的概率。是包含在事物之中并预示着实物发展趋势的量化指标。
数学中的可能性:
必然事件:100%。即一定会发生的事件。如:今天
是星期一,明天一定是星期二。
不确定事件:x%。即在主观或客观条件下都不能确定
是否会发生的事件,常用“不一定”、“经
常”、“可能”、“偶尔”等词语来描述。
如:今天下雨,明天不一定也要下雨。
不可能事件:0%。即在逻辑思维下不会发生的事件。
如:太阳不可能从西边升起。
在我们这个世界中,可能性不会超过1(100%)。
游戏的公平性:
(1)玩游戏时,游戏规则必须保证事件发生的可能性相同,这样游戏才公平。确定一个游戏是否公平,要先找出事件发生的所有可能,然后看对于游戏双方发生的可能性是否相同。若相同,游戏公平,如果不相同,游戏就不公平。
(2)判断一个游戏的公平性,关键是看参加游戏的各方获胜的机会是否均等。
(3)设计公平的游戏方案,应考虑两个方面:一是要让可能出现的结果是有限的;二是出现各种结果的可能性相等。
用几分之几来描述一个事件发生的可能性:
求一事件发生的可能性,要先找出这一事件所有可能出现的结果(假设有b种可能的结果),再找出所求事件发生的可能结果(假设有a种结果),那么这一事件发生的可能性就是 。
如:盒子里有2个白球、3个红球和4个绿球,摸到白球的可能性是 。
课
堂
习
练
第5课时
1、任意从装有10枚白子和12枚黑子的袋子里摸出1枚子,那么摸到(? )的可能性大,摸到( )的可能性小。
2、在下面的括号里填“一定”、“可能”、或“不可能”。
明天( )会下雨。
太阳( )从东边落下。
哈尔滨的冬天( )会下雪。
这次测验我( )会得100分。
3、从一副除去大、小王的扑克牌中任意抽取一张是5的概率为( )。???
黑子
白子
可能
不可能
一定
可能
4、某地的天气预报中说:“明天的降水率是80%。”根据这个预报,判断下面的说法是否正确。(正确的“√”,错误的“×”)
(1)明天一定下雨(?? )?????
(2)明天下雨的可能性很小(?? )
(3)明天不可能下雨(?? )???
(4)明天下雨的可能性很大(?? )
×
×
×
√
5、用1、2、3组成三位数,出现单数的可能性是 ;出现双数的可能性是 。
6、用2、3、4组成三位数,出现单数的可能性是 ;出现双数的可能性是 。
7、用1、2、3、4组成三位数,出现单数的可能性是 ;出现双数的可能性是 。
8、桌子上摆着9张卡片,分别写着1-9各数。如果摸到单数小明赢,如果摸到双数小红赢。
(1)这个游戏公平吗?
(2)小红一定会输吗?
(3)你能设计一个公平的规则吗?
