小学数学西师大版六年级下 总复习 图形与几何(2) 课件(35张PPT)
文档属性
| 名称 | 小学数学西师大版六年级下 总复习 图形与几何(2) 课件(35张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-04 00:00:00 | ||
图片预览




文档简介
复习立体图形
六年级下册第五单元
脑筋急转弯
拿着鸡蛋扔石头,为什么鸡蛋没摔破?
一个人在沙滩上行走,回头为什么看不见自己的脚印?
扔的是石头
退着走的
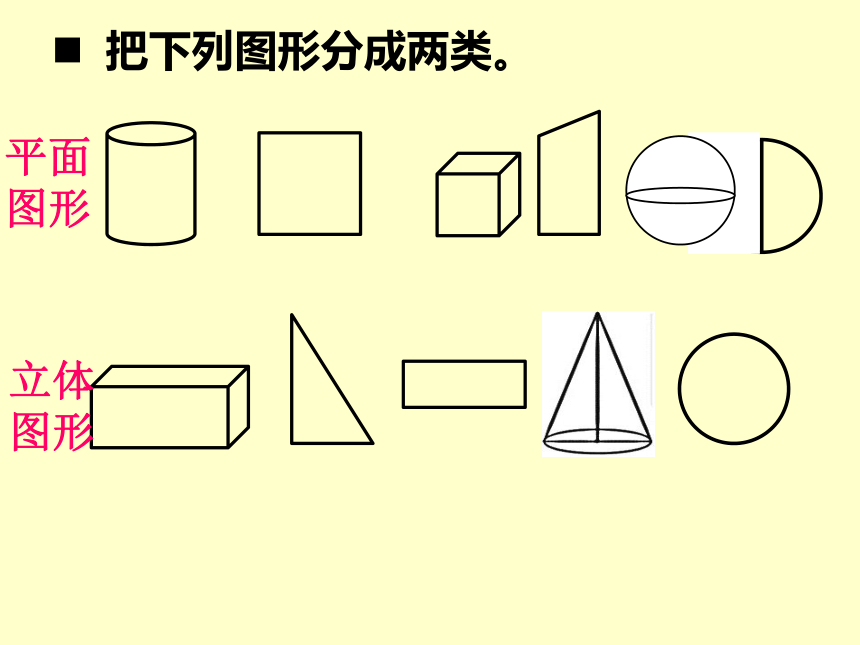
把下列图形分成两类。
平面图形
立体图形
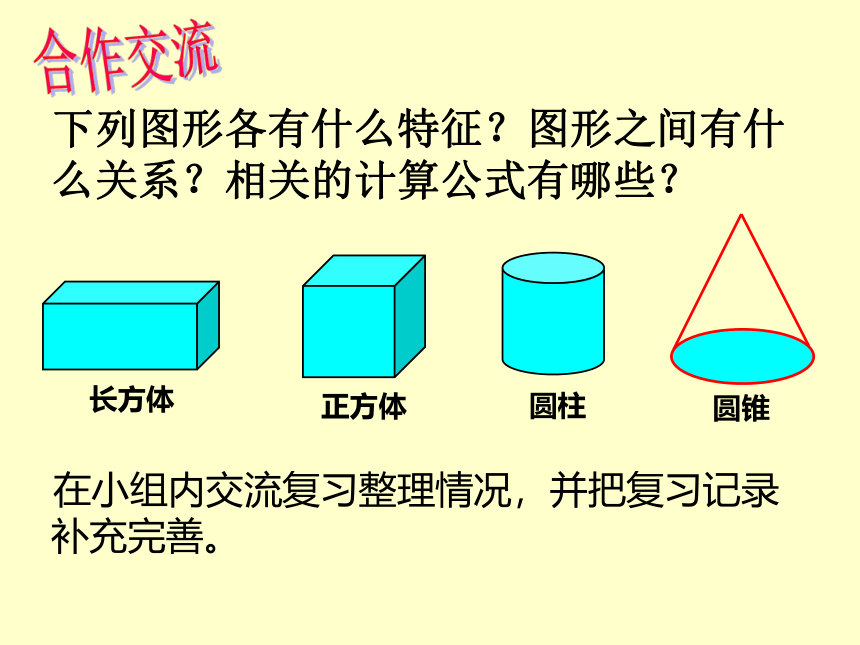
长方体
正方体
圆柱
圆锥
下列图形各有什么特征?图形之间有什么关系?相关的计算公式有哪些?
在小组内交流复习整理情况,并把复习记录补充完善。
立体
图形
顶点
棱
面
关系
条数
长短
个数
形状
大小
8个
12条
相对的4条棱长度相等
6个
6个面都是长方形,特殊情况有两个相对的面是正方形
相对的两个完全相同
8个
12条
12条棱长度相等
6个
6个面都是正方形
6个面完全相同
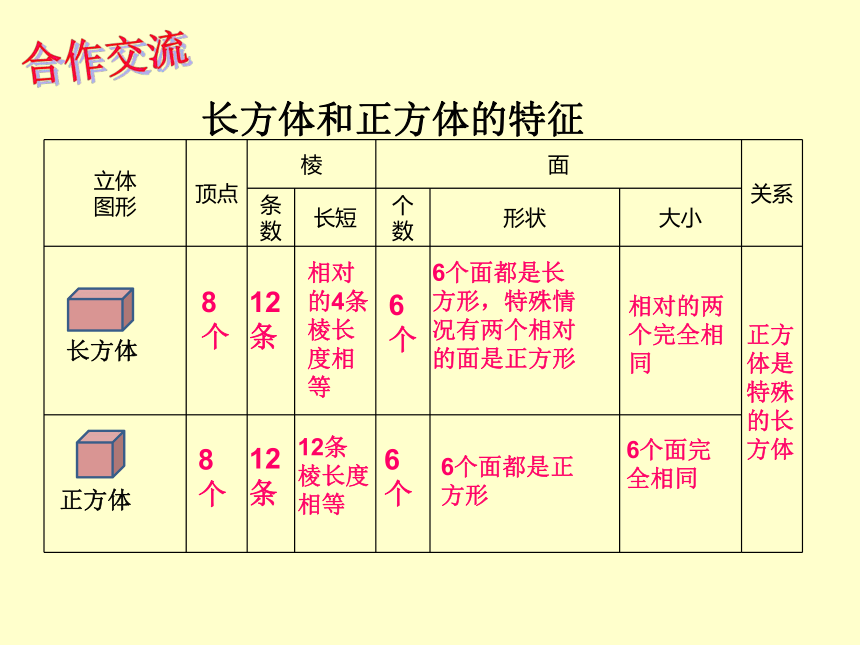
长方体
正方体
正方体是特殊的长方体
长方体和正方体的特征
立体
图形
面
高
关系
底面
侧面
2个底面是完全相同的圆
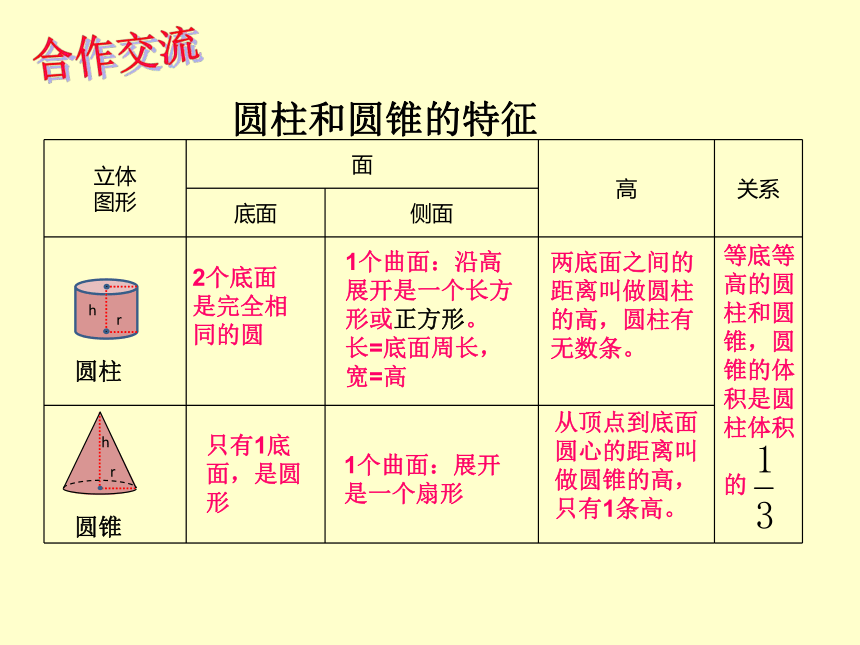
圆柱
圆锥
等底等高的圆柱和圆锥,圆锥的体积是圆柱体积
的
圆柱和圆锥的特征
r
h
r
h
1个曲面:沿高展开是一个长方形或正方形。
长=底面周长,宽=高
只有1底面,是圆形
1个曲面:展开是一个扇形
两底面之间的距离叫做圆柱的高,圆柱有无数条。
从顶点到底面圆心的距离叫做圆锥的高,只有1条高。
立体
图形
棱长总和(L)
表面积(S)
体积(或容积)
(V)
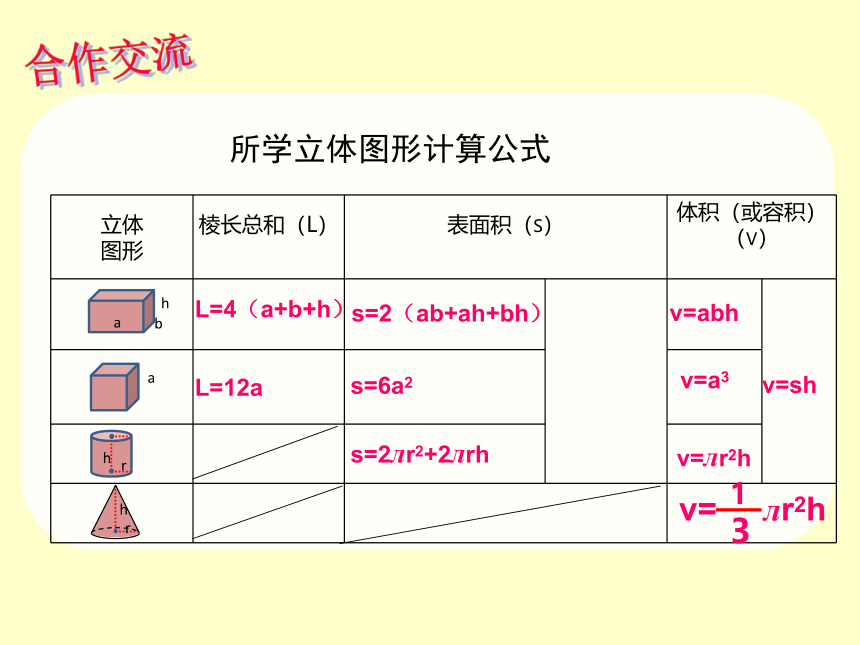
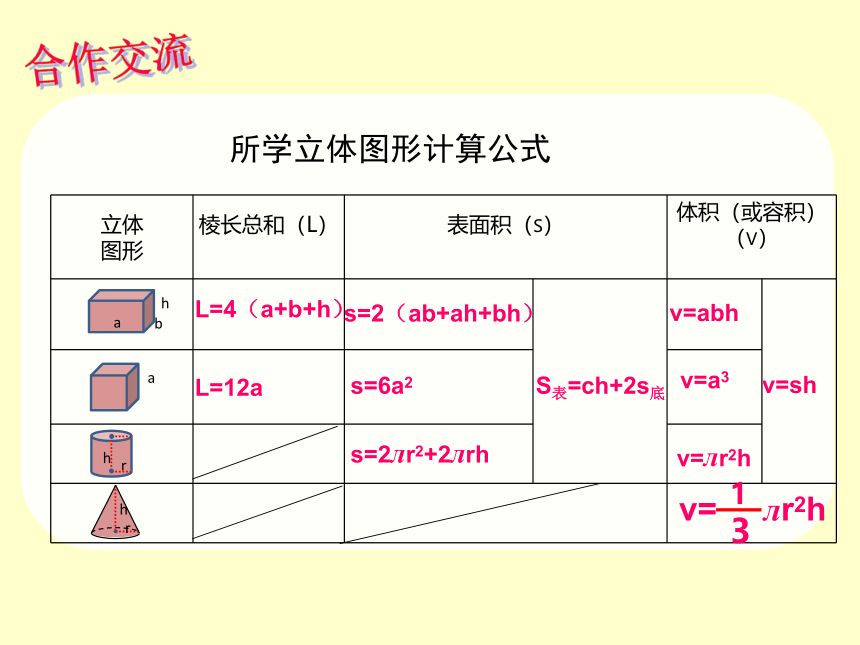
所学立体图形计算公式
a
b
h
a
r
h
r
h
L=4(a+b+h)
L=12a
s=2(ab+ah+bh)
s=6a2
s=2лr2+2лrh
v=abh
v=a3
v=лr2h
v=sh
v= лr2h
1
3
底面
底面
底面
上底面
上底面
上底面
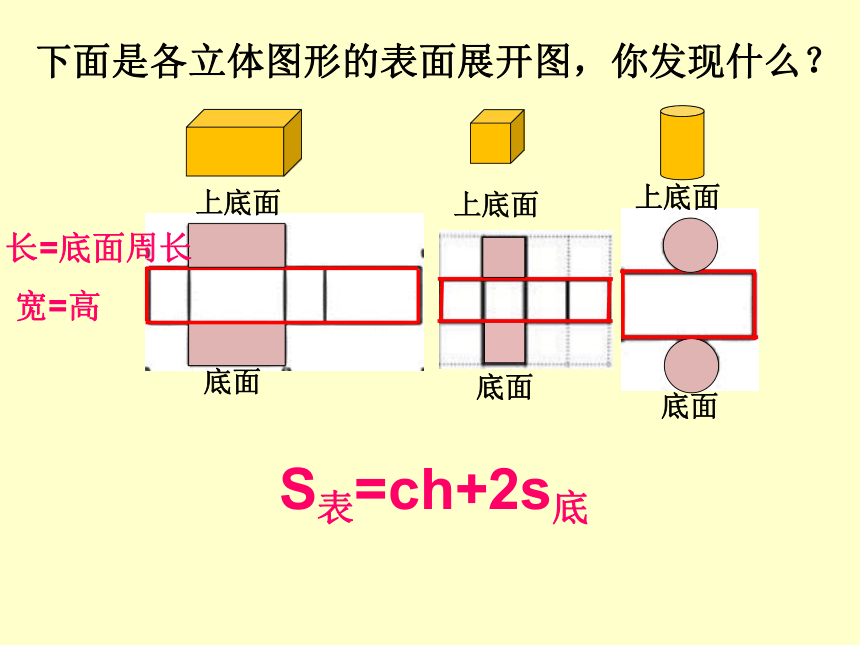
长=底面周长
宽=高
下面是各立体图形的表面展开图,你发现什么?
S表=ch+2s底
立体
图形
棱长总和(L)
表面积(S)
体积(或容积)
(V)
所学立体图形计算公式
a
b
h
a
r
h
r
h
L=4(a+b+h)
L=12a
s=2(ab+ah+bh)
s=6a2
s=2лr2+2лrh
v=abh
v=a3
v=лr2h
v=sh
v= лr2h
1
3
S表=ch+2s底
大厅里有一根底面直径6dm,高35dm圆柱形的柱子。
(1)这根柱子的占地面积是多少?是求它的( )
(2)这根柱子刷油漆的面积是多少?是求它的( )
(3)这根柱子占多大的空间,是求它的( )
1、选择正确答案的番号填入括号里。
A、表面积 B、体积 C、 侧面积 D、底面积 E 、侧面积+1个底面积
B
C
D
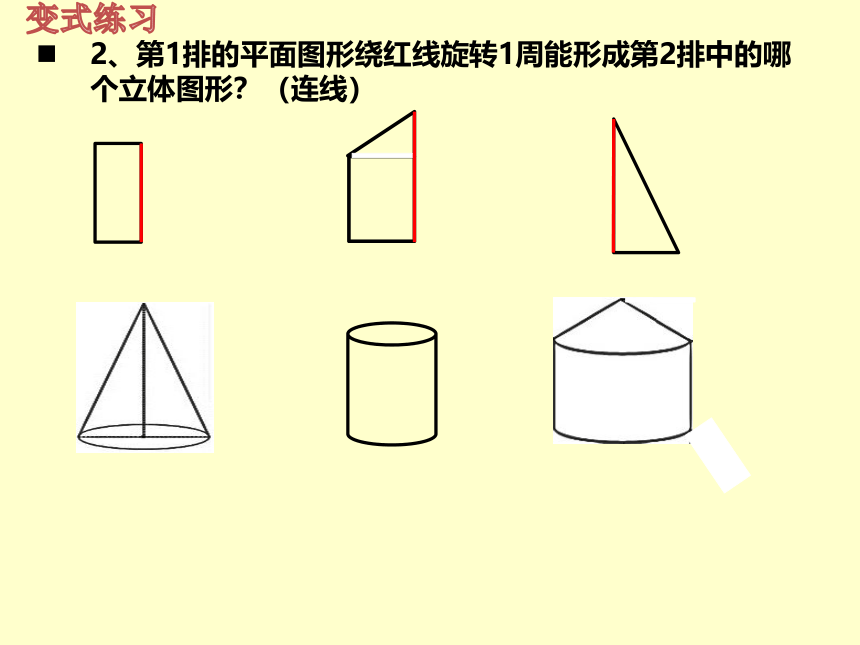
2、第1排的平面图形绕红线旋转1周能形成第2排中的哪个立体图形?(连线)
第1排的平面图形绕红线旋转1周能形成第2排中的哪个立体图形?(连线)
第1排的平面图形绕红线旋转1周,根据各平面图形的信息,算出旋转后得到的各立体图形的体积。(单位:cm)
6
2
3
5
3
4
5
3.14x22x6
3.14x32x4+ x3.14x32x(5-4)
x3.14x32x5
中心轴
角度
3、如果把第1排中的平面图形平放在桌面上,再竖直向上平移,留下的运动痕迹可能形成第2排的哪个立体图形?(连线)
提示:拿一张长方形纸试一试。
竖直向上平移的距离就是这个长方体的( )
高
5cm
如果第1排中的平面图形放在桌面上,再竖直向上平移可能形成第2排的哪个立体图形?(连线)
根据各平面图形的信息,如果竖直向上平移5cm后,形成的立体图形的表面积各是多少?(单位:cm)(只列式,不计算)
6
2
5
5
6
8
方法1:3.14x6x5÷2+3.14x(6÷2)2+6x5
方法2:(3.14x6÷2+6)x5+3.14x(6÷2)2
你能计算下图的表面积和体积吗?
3m
4m
5m
2m
你有什么收获?
点 线 面
动
动
动
体
10dm
20dm
形体
长方体
正方体
面
棱
点
面的形状
大小
棱长
6 个
12 条
8 个
6个面都是长方形,特殊情况有两个相对面是正方形。
相对的面完全相同
相对的4条棱长度相等
6 个
12 条
8 个
6个面都是
正方形
6个面完全相同
12条棱的长度都相等
相同点
不 同 点
关系
正方体是特殊的长方体
议一议
名称
基本特征
圆
柱
圆
锥
1. 上下两个底面是完全相同的两个圆;
2. 两个底面之间的距离叫做高;
3. 圆柱的侧面沿高展开是一个长方形。(长=底面周长,宽=高)
1. 底面是一个圆;
2. 从顶点到底面圆心的距离叫做高;
3. 侧面展开是一个扇形。
议一议
体积:是指物体所占空间的大小。
表面积:是指立体图形所有面的面积之和。
找一找
a
b
h
a
a
a
h
r
长方体表面积:
正方体表面积:
圆柱侧面积:
圆柱表面积:
S=(ab+ah+bh) ×2
S=6a
S侧=2лrh
S表=2лrh+ 2лr
2
2
表面积和体积复习
V=
V=
V=
V=
abh
a3
sh
1
3
sh
V = sh
正方体、长方体和圆柱有什么相似的地方呢?
h
a
b
a
a
a
s
h
s
h
想一想
第1排的平面图形绕红线旋转1周能形成第2排中的哪个立体图形?(连线)
第2排中的哪个立体图形是第1排对应的平面图形绕红线旋转1周形成的?(连线)
6
2
3
5
4
5
3
根据各平面图形的信息,算出旋转后得到的各立体图形的体积。(单位:cm)
如果把第2排的平面图形平放在桌面上,再竖直向上平移5cm后,形成的立体图形的表面积各是多少?(单位:cm)
6
5
2
5
8
6
立体图形的棱长总和、表面积、体积有什么区别?
1. 表示的意义不同;
2. 计量单位不同;
3. 计算方法不同。
找一找
立体
图形
特 征
棱长总和(L)
表面积公式
(S)
体积公式(容积)
(V)
所学立体图形的特征和计算公式
a
b
h
a
r
h
顶点:
棱:
面:
顶点:
棱:
面:
面:
高:
面:
高:
r
h
六年级下册第五单元
脑筋急转弯
拿着鸡蛋扔石头,为什么鸡蛋没摔破?
一个人在沙滩上行走,回头为什么看不见自己的脚印?
扔的是石头
退着走的
把下列图形分成两类。
平面图形
立体图形
长方体
正方体
圆柱
圆锥
下列图形各有什么特征?图形之间有什么关系?相关的计算公式有哪些?
在小组内交流复习整理情况,并把复习记录补充完善。
立体
图形
顶点
棱
面
关系
条数
长短
个数
形状
大小
8个
12条
相对的4条棱长度相等
6个
6个面都是长方形,特殊情况有两个相对的面是正方形
相对的两个完全相同
8个
12条
12条棱长度相等
6个
6个面都是正方形
6个面完全相同
长方体
正方体
正方体是特殊的长方体
长方体和正方体的特征
立体
图形
面
高
关系
底面
侧面
2个底面是完全相同的圆
圆柱
圆锥
等底等高的圆柱和圆锥,圆锥的体积是圆柱体积
的
圆柱和圆锥的特征
r
h
r
h
1个曲面:沿高展开是一个长方形或正方形。
长=底面周长,宽=高
只有1底面,是圆形
1个曲面:展开是一个扇形
两底面之间的距离叫做圆柱的高,圆柱有无数条。
从顶点到底面圆心的距离叫做圆锥的高,只有1条高。
立体
图形
棱长总和(L)
表面积(S)
体积(或容积)
(V)
所学立体图形计算公式
a
b
h
a
r
h
r
h
L=4(a+b+h)
L=12a
s=2(ab+ah+bh)
s=6a2
s=2лr2+2лrh
v=abh
v=a3
v=лr2h
v=sh
v= лr2h
1
3
底面
底面
底面
上底面
上底面
上底面
长=底面周长
宽=高
下面是各立体图形的表面展开图,你发现什么?
S表=ch+2s底
立体
图形
棱长总和(L)
表面积(S)
体积(或容积)
(V)
所学立体图形计算公式
a
b
h
a
r
h
r
h
L=4(a+b+h)
L=12a
s=2(ab+ah+bh)
s=6a2
s=2лr2+2лrh
v=abh
v=a3
v=лr2h
v=sh
v= лr2h
1
3
S表=ch+2s底
大厅里有一根底面直径6dm,高35dm圆柱形的柱子。
(1)这根柱子的占地面积是多少?是求它的( )
(2)这根柱子刷油漆的面积是多少?是求它的( )
(3)这根柱子占多大的空间,是求它的( )
1、选择正确答案的番号填入括号里。
A、表面积 B、体积 C、 侧面积 D、底面积 E 、侧面积+1个底面积
B
C
D
2、第1排的平面图形绕红线旋转1周能形成第2排中的哪个立体图形?(连线)
第1排的平面图形绕红线旋转1周能形成第2排中的哪个立体图形?(连线)
第1排的平面图形绕红线旋转1周,根据各平面图形的信息,算出旋转后得到的各立体图形的体积。(单位:cm)
6
2
3
5
3
4
5
3.14x22x6
3.14x32x4+ x3.14x32x(5-4)
x3.14x32x5
中心轴
角度
3、如果把第1排中的平面图形平放在桌面上,再竖直向上平移,留下的运动痕迹可能形成第2排的哪个立体图形?(连线)
提示:拿一张长方形纸试一试。
竖直向上平移的距离就是这个长方体的( )
高
5cm
如果第1排中的平面图形放在桌面上,再竖直向上平移可能形成第2排的哪个立体图形?(连线)
根据各平面图形的信息,如果竖直向上平移5cm后,形成的立体图形的表面积各是多少?(单位:cm)(只列式,不计算)
6
2
5
5
6
8
方法1:3.14x6x5÷2+3.14x(6÷2)2+6x5
方法2:(3.14x6÷2+6)x5+3.14x(6÷2)2
你能计算下图的表面积和体积吗?
3m
4m
5m
2m
你有什么收获?
点 线 面
动
动
动
体
10dm
20dm
形体
长方体
正方体
面
棱
点
面的形状
大小
棱长
6 个
12 条
8 个
6个面都是长方形,特殊情况有两个相对面是正方形。
相对的面完全相同
相对的4条棱长度相等
6 个
12 条
8 个
6个面都是
正方形
6个面完全相同
12条棱的长度都相等
相同点
不 同 点
关系
正方体是特殊的长方体
议一议
名称
基本特征
圆
柱
圆
锥
1. 上下两个底面是完全相同的两个圆;
2. 两个底面之间的距离叫做高;
3. 圆柱的侧面沿高展开是一个长方形。(长=底面周长,宽=高)
1. 底面是一个圆;
2. 从顶点到底面圆心的距离叫做高;
3. 侧面展开是一个扇形。
议一议
体积:是指物体所占空间的大小。
表面积:是指立体图形所有面的面积之和。
找一找
a
b
h
a
a
a
h
r
长方体表面积:
正方体表面积:
圆柱侧面积:
圆柱表面积:
S=(ab+ah+bh) ×2
S=6a
S侧=2лrh
S表=2лrh+ 2лr
2
2
表面积和体积复习
V=
V=
V=
V=
abh
a3
sh
1
3
sh
V = sh
正方体、长方体和圆柱有什么相似的地方呢?
h
a
b
a
a
a
s
h
s
h
想一想
第1排的平面图形绕红线旋转1周能形成第2排中的哪个立体图形?(连线)
第2排中的哪个立体图形是第1排对应的平面图形绕红线旋转1周形成的?(连线)
6
2
3
5
4
5
3
根据各平面图形的信息,算出旋转后得到的各立体图形的体积。(单位:cm)
如果把第2排的平面图形平放在桌面上,再竖直向上平移5cm后,形成的立体图形的表面积各是多少?(单位:cm)
6
5
2
5
8
6
立体图形的棱长总和、表面积、体积有什么区别?
1. 表示的意义不同;
2. 计量单位不同;
3. 计算方法不同。
找一找
立体
图形
特 征
棱长总和(L)
表面积公式
(S)
体积公式(容积)
(V)
所学立体图形的特征和计算公式
a
b
h
a
r
h
顶点:
棱:
面:
顶点:
棱:
面:
面:
高:
面:
高:
r
h
