19.2.3一次函数与方程、不等式(第2课时) 课件 2020-2021学年人教版数学 八年级下册(共31张ppt)
文档属性
| 名称 | 19.2.3一次函数与方程、不等式(第2课时) 课件 2020-2021学年人教版数学 八年级下册(共31张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 809.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-06 00:00:00 | ||
图片预览








文档简介
人教版 · 数学· 八年级(下)
第19章 一次函数
19.2.3 一次函数与方程、不等式
第2课时 一次函数与一元一次方程、不等式
1.理解一次函数与一元一次不等式的关系。
2.会根据一次函数图象求解一元一次不等式。
学习目标
1.解下列一元一次不等式:
(1)3x+1>0
(2)5y-2≤3
解:∵3x+1>0
∴3x>-1
解得:x>-13
?
解:∵5y-2≤3
∴5y ≤ 5
解得:y≤1
回顾旧知
2.利用函数图象解方程:5x-1=2x+8.
解:将方程 5x-1=2x+8 变形为 3x-9=0
画出函数 y=3x-9 的图象
由图象可知:直线 y=3x-9 与 x 轴的交点为(3,0)
即 x=3 是方程的解.
y
x
O
3
-9
y=3x-9
解一元一次不等式:3x+2>0.
当自变量x的值为多少时,一次函数y=3x+2的函数值大于0?
导入新知
解一元一次不等式:3x+2<0.
当自变量x的值为多少时,一次函数y=3x+2的函数值小于0?
解一元一次不等式:kx+b>0(k≠0), kx+b<0(k≠0).
当自变量x的值为多少时,一次函数y=kx+b的函数值大于0,小于0?
仔细观察以上三组例子,你能发现什么?
新知 一次函数与一元一次不等式的关系
从以上三组例子可以看出:每一组看似是两个问题,其实结果一样,只是表达方式不一样.我们分别比较解一元一次不等式和判断一次函数的函数值正负性,探究二者之间的关系.
合作探究
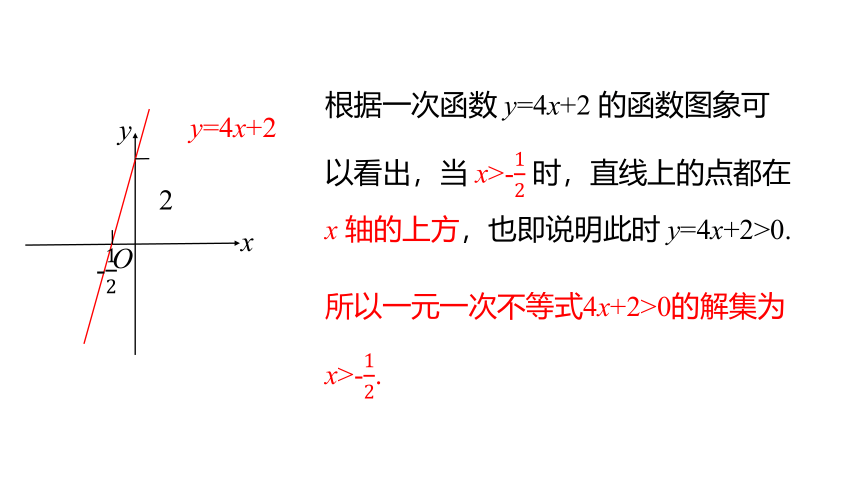
根据一次函数 y=4x+2 的函数图象可以看出,当 x>-12 时,直线上的点都在x 轴的上方,也即说明此时 y=4x+2>0.
?
所以一元一次不等式4x+2>0的解集为
x>-12.
?
y
x
O
2
-12
?
y=4x+2
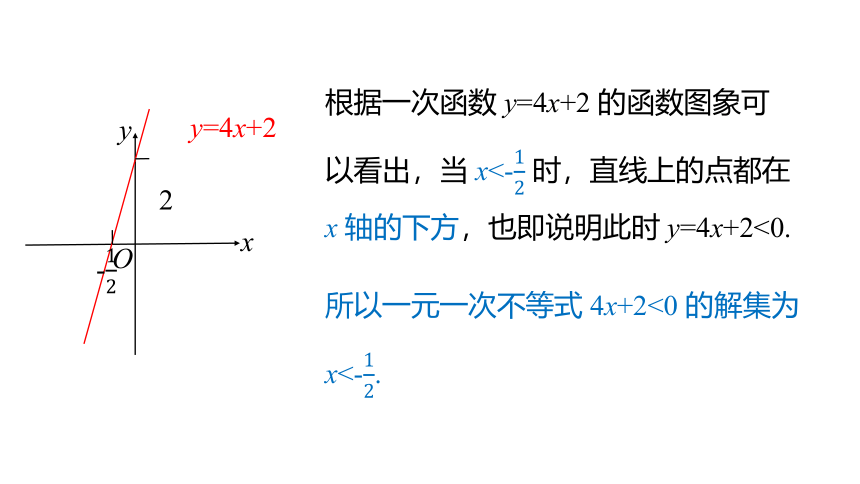
根据一次函数 y=4x+2 的函数图象可以看出,当 x<-12 时,直线上的点都在x 轴的下方,也即说明此时 y=4x+2<0.
?
所以一元一次不等式 4x+2<0 的解集为
x<-12.
?
y
x
O
2
-12
?
y=4x+2
因为任何一个以 x 为未知数的一元一次不等式都可以变形为 kx+b>0(k≠0)或 kx+b<0(k≠0)的形式,所以解一元一次不等式可以看作是求一次函数 y=kx+b 的函数值大于 0 或小于 0 时,自变量 x 的取值范围.
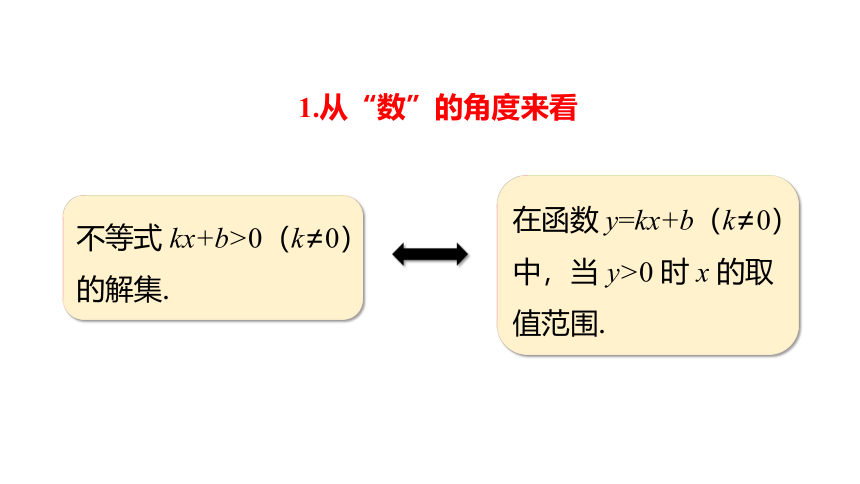
1.从“数”的角度来看
不等式 kx+b>0(k≠0)的解集.
在函数 y=kx+b(k≠0)中,当 y>0 时 x 的取值范围.
1.从“数”的角度来看
不等式 kx+b<0(k≠0)的解集.
在函数 y=kx+b(k≠0)中,当 y<0 时 x 的取值范围.
2.从“形”的角度来看
不等式 kx+b>0(k≠0)的解集.
直线 y=kx+b(k≠0)在 x 轴上方的部分所对应的 x 的取值范围.
2.从“形”的角度来看
不等式 kx+b<0(k≠0)的解集.
直线 y=kx+b(k≠0)在 x 轴下方的部分所对应的 x 的取值范围.
y
x
O
y1=k1x+b1
y2=k2x+b2
直线 y1=k1x+b1 与直线 y2=k2x+b2 的交点的横坐标即是方程 k1x+b1=k2x+b2的解;不等式 y1>y2(或 y1拓展
P
1.根据下列一次函数的图象,直接写出一元一次不等式的解集.
(1)一元一次不等式 12x+1>0 的解集为: .
?
(2)一元一次不等式 12x+1<0 的解集为: .
?
x>-2
x<-2
y
x
O
1
-2
y=12x+1
?
巩固新知
2.函数 y=-x+3 的图象如图所示,请正确填写以下空格.
(1)当x取 时,函数图象在
x 轴下方.
(2)当x取 时,函数图象在
x 轴上方.
x>3
x<3
y
x
O
3
3
y=-x+3
一次函数与一元一次不等式
关系
步骤
①从“数”的角度;
②从“形”的角度.
①一元一次不等式看函数图象与x轴的交点;
②一元一次不等式组看两个函数图象交点的横坐标.
归纳新知
1.如图,直线y=ax+b过点A(0,2)和点B(-3,0),
则方程ax+b=0的解是( )
A.x=2 B.x=0
C.x=-1 D.x=-3
2.一次函数y=kx+b(k,b为常数,k≠0)的图象如图所示,
根据图象信息可求得关于x的方程kx+b=3的解为______.
D
x=2
课堂练习
3.如图是函数y=kx+b(k,b是常数,且k≠0)的图象,利用图象直接写出:
(1)方程kx+b=0的解;
(2)方程kx+b=-2的解;
(3)方程kx+b=-3的解.
解:(1)x=2 (2)x=0 (3)x=-1
4.用图象法解方程:3x-6=0.
解:图象略,x=2
A
A
7.直线y=kx+3经过点A(2,1),则不等式kx+3≥1的解集是_______.
8.如图,直线y=kx+b(k≠0)与x轴的交点为(2,0),与y轴的交点
为(0,3),则关于x的不等式0<kx+b<3的解集是_____________.
x≤2
0<x<2
C
D
11.已知y=kx+2,当x<-1时,其图象在x轴下方;
当x>-1时,其图象在x轴上方,则k=____.
12.如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),
则关于x的不等式x+1≥mx+n的解集为________.
2
x≥1
13.画出函数y=-x+3的图象,并利用图象回答:
(1)当x=-1时,y等于多少?
(2)当y=-1时,x等于多少?
(3)方程-x+3=0的解是多少?
(4)图象与两坐标轴围成的三角形的面积是多少?
14.小华准备将平时的零用钱节约一些储存起来,他已存有62元,从现在起每个月存12元,小华的同学小丽以前没有存过零用钱,听到小华在存零用钱,表示从现在起每个月存20元,争取超过小华.
(1)试写出小华的存款总数y1与从现在开始的月数x之间的函数关系式以及小丽的存款总数y2与月数x之间的函数关系式;
(2)从第几个月开始小丽的存款数可以超过小华?
15.如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,
求关于x的不等式组-x+m>nx+4n>0的整数解.
解:由题意可得不等式-x+m>nx+4n的解集为x<-2,
∵y=nx+4n=0时,x=-4,∴nx+4n>0的解集是x>-4,
∴-x+m>nx+4n>0的解集是-4<x<-2,∴整数解为-3
16.如图,反映了甲、乙两名自行车运动员在公路上进行训练的行驶路程s(千米)和行驶时间t(小时)之间的关系,根据所给图象,解答下列问题:
(1)写出甲的行驶路程s和行驶时间t(t≥0)之间的函数关系式;
(2)在哪一段时间内,甲的行驶速度小于乙的行驶速度;
在哪一段时间内,甲的行驶速度大于乙的行驶速度;
(3)从图中你能获得什么信息?请写出其中的一条.
解:(1)s=2t
(2)在0<t<1时,甲的的行驶速度小于乙的行驶速度;
在t>1时,甲的行驶速度大于乙的行驶速度
(3)说法合乎情理即可,如当出发3小时时,甲乙相遇等等
再见
第19章 一次函数
19.2.3 一次函数与方程、不等式
第2课时 一次函数与一元一次方程、不等式
1.理解一次函数与一元一次不等式的关系。
2.会根据一次函数图象求解一元一次不等式。
学习目标
1.解下列一元一次不等式:
(1)3x+1>0
(2)5y-2≤3
解:∵3x+1>0
∴3x>-1
解得:x>-13
?
解:∵5y-2≤3
∴5y ≤ 5
解得:y≤1
回顾旧知
2.利用函数图象解方程:5x-1=2x+8.
解:将方程 5x-1=2x+8 变形为 3x-9=0
画出函数 y=3x-9 的图象
由图象可知:直线 y=3x-9 与 x 轴的交点为(3,0)
即 x=3 是方程的解.
y
x
O
3
-9
y=3x-9
解一元一次不等式:3x+2>0.
当自变量x的值为多少时,一次函数y=3x+2的函数值大于0?
导入新知
解一元一次不等式:3x+2<0.
当自变量x的值为多少时,一次函数y=3x+2的函数值小于0?
解一元一次不等式:kx+b>0(k≠0), kx+b<0(k≠0).
当自变量x的值为多少时,一次函数y=kx+b的函数值大于0,小于0?
仔细观察以上三组例子,你能发现什么?
新知 一次函数与一元一次不等式的关系
从以上三组例子可以看出:每一组看似是两个问题,其实结果一样,只是表达方式不一样.我们分别比较解一元一次不等式和判断一次函数的函数值正负性,探究二者之间的关系.
合作探究
根据一次函数 y=4x+2 的函数图象可以看出,当 x>-12 时,直线上的点都在x 轴的上方,也即说明此时 y=4x+2>0.
?
所以一元一次不等式4x+2>0的解集为
x>-12.
?
y
x
O
2
-12
?
y=4x+2
根据一次函数 y=4x+2 的函数图象可以看出,当 x<-12 时,直线上的点都在x 轴的下方,也即说明此时 y=4x+2<0.
?
所以一元一次不等式 4x+2<0 的解集为
x<-12.
?
y
x
O
2
-12
?
y=4x+2
因为任何一个以 x 为未知数的一元一次不等式都可以变形为 kx+b>0(k≠0)或 kx+b<0(k≠0)的形式,所以解一元一次不等式可以看作是求一次函数 y=kx+b 的函数值大于 0 或小于 0 时,自变量 x 的取值范围.
1.从“数”的角度来看
不等式 kx+b>0(k≠0)的解集.
在函数 y=kx+b(k≠0)中,当 y>0 时 x 的取值范围.
1.从“数”的角度来看
不等式 kx+b<0(k≠0)的解集.
在函数 y=kx+b(k≠0)中,当 y<0 时 x 的取值范围.
2.从“形”的角度来看
不等式 kx+b>0(k≠0)的解集.
直线 y=kx+b(k≠0)在 x 轴上方的部分所对应的 x 的取值范围.
2.从“形”的角度来看
不等式 kx+b<0(k≠0)的解集.
直线 y=kx+b(k≠0)在 x 轴下方的部分所对应的 x 的取值范围.
y
x
O
y1=k1x+b1
y2=k2x+b2
直线 y1=k1x+b1 与直线 y2=k2x+b2 的交点的横坐标即是方程 k1x+b1=k2x+b2的解;不等式 y1>y2(或 y1
P
1.根据下列一次函数的图象,直接写出一元一次不等式的解集.
(1)一元一次不等式 12x+1>0 的解集为: .
?
(2)一元一次不等式 12x+1<0 的解集为: .
?
x>-2
x<-2
y
x
O
1
-2
y=12x+1
?
巩固新知
2.函数 y=-x+3 的图象如图所示,请正确填写以下空格.
(1)当x取 时,函数图象在
x 轴下方.
(2)当x取 时,函数图象在
x 轴上方.
x>3
x<3
y
x
O
3
3
y=-x+3
一次函数与一元一次不等式
关系
步骤
①从“数”的角度;
②从“形”的角度.
①一元一次不等式看函数图象与x轴的交点;
②一元一次不等式组看两个函数图象交点的横坐标.
归纳新知
1.如图,直线y=ax+b过点A(0,2)和点B(-3,0),
则方程ax+b=0的解是( )
A.x=2 B.x=0
C.x=-1 D.x=-3
2.一次函数y=kx+b(k,b为常数,k≠0)的图象如图所示,
根据图象信息可求得关于x的方程kx+b=3的解为______.
D
x=2
课堂练习
3.如图是函数y=kx+b(k,b是常数,且k≠0)的图象,利用图象直接写出:
(1)方程kx+b=0的解;
(2)方程kx+b=-2的解;
(3)方程kx+b=-3的解.
解:(1)x=2 (2)x=0 (3)x=-1
4.用图象法解方程:3x-6=0.
解:图象略,x=2
A
A
7.直线y=kx+3经过点A(2,1),则不等式kx+3≥1的解集是_______.
8.如图,直线y=kx+b(k≠0)与x轴的交点为(2,0),与y轴的交点
为(0,3),则关于x的不等式0<kx+b<3的解集是_____________.
x≤2
0<x<2
C
D
11.已知y=kx+2,当x<-1时,其图象在x轴下方;
当x>-1时,其图象在x轴上方,则k=____.
12.如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),
则关于x的不等式x+1≥mx+n的解集为________.
2
x≥1
13.画出函数y=-x+3的图象,并利用图象回答:
(1)当x=-1时,y等于多少?
(2)当y=-1时,x等于多少?
(3)方程-x+3=0的解是多少?
(4)图象与两坐标轴围成的三角形的面积是多少?
14.小华准备将平时的零用钱节约一些储存起来,他已存有62元,从现在起每个月存12元,小华的同学小丽以前没有存过零用钱,听到小华在存零用钱,表示从现在起每个月存20元,争取超过小华.
(1)试写出小华的存款总数y1与从现在开始的月数x之间的函数关系式以及小丽的存款总数y2与月数x之间的函数关系式;
(2)从第几个月开始小丽的存款数可以超过小华?
15.如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,
求关于x的不等式组-x+m>nx+4n>0的整数解.
解:由题意可得不等式-x+m>nx+4n的解集为x<-2,
∵y=nx+4n=0时,x=-4,∴nx+4n>0的解集是x>-4,
∴-x+m>nx+4n>0的解集是-4<x<-2,∴整数解为-3
16.如图,反映了甲、乙两名自行车运动员在公路上进行训练的行驶路程s(千米)和行驶时间t(小时)之间的关系,根据所给图象,解答下列问题:
(1)写出甲的行驶路程s和行驶时间t(t≥0)之间的函数关系式;
(2)在哪一段时间内,甲的行驶速度小于乙的行驶速度;
在哪一段时间内,甲的行驶速度大于乙的行驶速度;
(3)从图中你能获得什么信息?请写出其中的一条.
解:(1)s=2t
(2)在0<t<1时,甲的的行驶速度小于乙的行驶速度;
在t>1时,甲的行驶速度大于乙的行驶速度
(3)说法合乎情理即可,如当出发3小时时,甲乙相遇等等
再见
