11.5 用一元一次不等式解决问题(2) 课件 2020-2021学年七年级数学苏科版下册(共18张ppt)
文档属性
| 名称 | 11.5 用一元一次不等式解决问题(2) 课件 2020-2021学年七年级数学苏科版下册(共18张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 16.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-06 00:00:00 | ||
图片预览






文档简介
解一元一次不等式的一般步骤:
1)去分母;每一项都要乘以最小公倍数,分子要加括号,负数不能漏
2)去括号;括号外面是负号的,括号内每一项要改变负号
3)移项;未知数项放在左边,常数项放在右边,移项要改变符号
4)合并同类项;
5)未知数的系数化为1. 如果未知数的系数是负数,不等号的方向要改变.不等式右边要乘以未知数系数的倒数
知识点回顾:
11.5 用一元一次不等式
解 决 问 题(2)
苏科版 七年级下
一元一次不等式解决实际问题的步骤是什么?
1.审清题意
2.找出一个能表示实际问题意义的不等关系
4.列不等式
5.解不等式,并检验答案是否符合题意
6.答 注意:根据题目实际有时需选取整数解
3.设未知数
注意:
设不写“最多”、“至少”……
学习目标
能够找出问题中的不等关系并列出一元一次不等式解决简单的实际问题.
学习目标
难点
寻找实际问题中的不等关系,建立数学模型。
1.某工程队计划在10天整修河堤600m.施工2天修了120m后,该工程需要比原计划提前2天完成,此后平均每天至少要整修河堤多少米?
限时任务题型
题型分析:
1、题中含有不等关系的语句_____________________________________。
2、将不等关系转化为不等式,即_________________________________。
3、假设此后平均每天要整修河堤x米,根据题干内容,实际工期为_______________天。
该工程需要比原计划提前2天完成
实际工期≤原计划工期-2
2+(600-120)/x
4.我们需要对限时任务题目重新理解:_________________________________。
2天的完成量+剩下6天的可完成量≥600m
注意:分母出现未知数!
改变思路:
求出工作量!
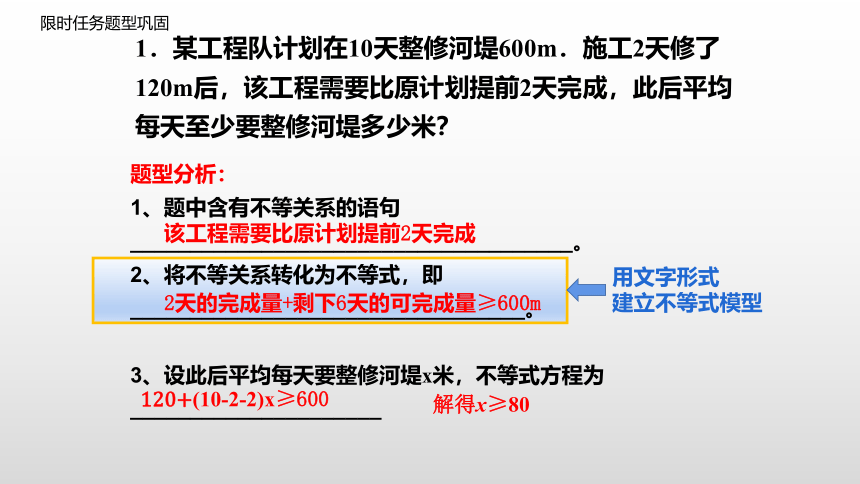
1.某工程队计划在10天整修河堤600m.施工2天修了120m后,该工程需要比原计划提前2天完成,此后平均每天至少要整修河堤多少米?
限时任务题型巩固
题型分析:
1、题中含有不等关系的语句_____________________________________。
2、将不等关系转化为不等式,即_________________________________。
3、设此后平均每天要整修河堤x米,不等式方程为_____________________
解得x≥80
该工程需要比原计划提前2天完成
2天的完成量+剩下6天的可完成量≥600m
120+(10-2-2)x≥600
用文字形式
建立不等式模型
情景引入
1. 某人骑一辆变速自行车,如果行驶增加4km/h,那么2h所行驶的路程不少于以原来速度2.5h所行驶的路程.原来行驶的速度最大是多少?
分析:
1、题中含有不等关系的语句_____________________________________。
2、将不等关系转化为不等式,即_________________________________。
3、假设原来行驶的速度为x km/h,根据题干内容,提速后的速度为_______________。
4、不等式方程为______
2h所行驶的路程不少于以原来速度2.5h所行驶的路程
x+4
2h所行驶的路程>原来速度2.5h所行驶的路程
2(x+4)≥2.5x
限时任务题型:
1.时间是有限制要求
2.已完成量(路程)+剩余时间内按效率/速度预算的量(路程) ≥ (或>) 计划量(路程)
3.剩余时间内按效率/速度预算的量(路程)是未发生,不确定的
2.某车间计划在15天内至少加工零件408个,前3天每天加工零件24个。此后,该车工平均每天至少需要加工零件多少个,才能在规定时间内完成任务?
限时任务题型巩固
题型分析:
1、题中含有不等关系的语句_____________________________________。
2、将不等关系转化为不等式,即_________________________________。
3、设平均每天需要加工零件x个,不等式方程为__________________
解得x≥28
15天内至少加工零件408个
前三天完成量+剩余时间完成量≥408个
24×3+(15-3)x≥408
3.某工地要实施爆破,导火线的燃烧速度是0.8cm/s,引爆人在点燃导火线后要跑到200m以外的安全区域.如果引爆人跑步的速度是5m/s,那么导火线的长度应大于多少?
3.某工地要实施爆破,导火线的燃烧速度是0.8cm/s,引爆人在点燃导火线后要跑到200m以外的安全区域.如果引爆人跑步的速度是5m/s,那么导火线的长度应大于多少?
限时任务题型巩固-限时逃脱
题型分析:
1、题中含有不等关系的语句_____________________________________。
2、将不等关系转化为不等式,即_________________________________。
3、设导火线的长度为x cm,不等式方程为__________________
点燃导火线后要跑到200m以外的安全区域
爆炸前跑出的路程>200m
解得x>32
单位统一问题:保证同级别的运算 单位统一即可
情景引入
1. 某人骑一辆变速自行车,如果行驶增加4km/h,那么2h所行驶的路程不少于以原来速度2.5h所行驶的路程.原来行驶的速度最大是多少?
分析:
1、题中含有不等关系的语句_____________________________________。
2、将不等关系转化为不等式,即_________________________________。
3、假设原来行驶的速度为x km/h,根据题干内容,提速后的速度为_______________。
4、不等式方程为______
2h所行驶的路程不少于以原来速度2.5h所行驶的路程
x+4
2h所行驶的路程>原来速度2.5h所行驶的路程
2(x+4)≥2.5x
关于折扣:
打几折:售价是标价的百分之几十
打几几折:售价是标价的百分之几十几。
对客户而言,折扣是打得越多越好,因为售价会越便宜。
售价=标价(不变)×折扣比率,对应的折扣比率(若设为x,x<1)就越小;
反过来,对商家来说折扣过多,有亏本的风险 ,一般说“最多打几折销售”
4.某超市进了某种糖果 1000kg,进价是7元/kg,售价定为10元/kg,销售一半以后,为了尽快售完,准备打折出售。如果要使总利润不低于2000元,那么余下的糖果可以按原定价最多打几折出售?
保证利润题型
题型分析:
1、题中含有不等关系的语句_____________________________________。
2、将不等关系转化为不等式,即_________________________________。
3、设折扣比率为x,不等式方程为__________________________________________
解得x≥80%
总利润不低于2000元
第一次销售额+第二次销售额-进价≥2000元
(1000×0.5)×10+(1000×0.5)×10x-1000×7≥2000
相关公式:标价*折扣比例=售价
售价-进价=利润
情景引入
1. 某人骑一辆变速自行车,如果行驶增加4km/h,那么2h所行驶的路程不少于以原来速度2.5h所行驶的路程.原来行驶的速度最大是多少?
分析:
1、题中含有不等关系的语句_____________________________________。
2、将不等关系转化为不等式,即_________________________________。
3、假设原来行驶的速度为x km/h,根据题干内容,提速后的速度为_______________。
4、不等式方程为______
2h所行驶的路程不少于以原来速度2.5h所行驶的路程
x+4
2h所行驶的路程>原来速度2.5h所行驶的路程
2(x+4)≥2.5x
保证利润题型:
1.保证利润:利润不低于,利润率不低于
2. 解题思路:总售价-总成本≥预期的利润额
3. 利润额=成本×利润率
4.成本控制:总成本是低于或不高于某一金额
5.解题思路:各项成本之和<控制成本
5.某商品的成本为2000元,标价为2800元,如果商店要以利润不低于5%的价格销售,那么最低可以打几折出售这些商品?
保证利润题型巩固
题型分析:
1、题中含有不等关系的语句_____________________________________。
2、将不等关系转化为不等式,即_________________________________。
3、假设折扣比率为x,不等式方程为__________________
解得x≥75%
利润不低于5%
售价-成本≥5%的利润额
2800x-2000≥2000×5%
相关公式:标价*折扣比例=售价 售价-成本=利润
利润=成本×利润率(百分比)
售价-进价=利润
6.某房地产开发商用2600万元购买了一块地用于建造居民住宅楼,如住宅楼每平米的造价约为1400元,那么建筑面积必须超过多少平方米才能将建楼成本控制在每平米4000元以下?
6.某房地产开发商用2600万元购买了一块地用于建造居民住宅楼,如住宅楼每平米的造价约为1400元,那么建筑面积必须超过多少平方米才能将建楼成本控制在每平米4000元以下?
保证利润-成本控制题型巩固
保证利润题型分析:
1、题中含有不等关系的语句_____________________________________。
2、将不等关系转化为不等式,即_________________________________。
3、假设建筑面积为x平方米,根据题干内容,___________________________。
4、不等式方程为__________________
解得x>10000
建楼成本控制在每平米4000元以下
建楼每平方米成本=(26000000+1400x)/x
建楼每平方米成本<4000元
26000000+1400x<4000x
注意:分母出现未知数!
地价+实际造价<4000元单价对应的建楼成本(控制成本)
地价+实际造价=26000000+1400x
关键:
与控制成本比较!
A.计算题解的检验
1.不等式计算题中,如
解:
1.上一题解得 x>10000
问题:“建筑面积必须超过多少平方米”
出现“超过”,建筑面积的解集
应带“>”“≥”
去分母 2(-2x+1)≥-x+8去括号 -4x+2≥-x+8
移项 -4x+x≥+8-2
合并同类项 -3x≥6
系数化为1 x≤-2
B.应用题解的检验
2.检验解集不等号:检查倒数第二行 -3x≥6 未知数系数是负数,所以符号改变是正确的
3. 检验解集数字:将x=-2代入 左边=右边,所以数字也是正确的
2.总结: 根据最后问题验证解集的符号
①含有大于、超过、至少、最少、最低 、最小,解集应带“>”“≥”
②含有小于、至多、最多、最高 、最大,
解集应带“<”“≤”
例外: “打折”
课后回顾
寻找实际问题中的不等关系
01
课后回顾
建立数学模型
02
利用解不等式
解决简单实际问题
03
8.某童装店按每套90元的价格购进40套童装,应缴纳的税费为销售额的10%. 如果要获得不低于900元的纯利润,每套童装的售价至少是多少元?
练习巩固:
7.甲、乙两地相距100km,一批物资需要在1h内从甲地送到乙地。某人驾驶汽车,前半小时走了40km,后半小时的速度至少为多少才能保证这批物资及时送到?
THE END
1)去分母;每一项都要乘以最小公倍数,分子要加括号,负数不能漏
2)去括号;括号外面是负号的,括号内每一项要改变负号
3)移项;未知数项放在左边,常数项放在右边,移项要改变符号
4)合并同类项;
5)未知数的系数化为1. 如果未知数的系数是负数,不等号的方向要改变.不等式右边要乘以未知数系数的倒数
知识点回顾:
11.5 用一元一次不等式
解 决 问 题(2)
苏科版 七年级下
一元一次不等式解决实际问题的步骤是什么?
1.审清题意
2.找出一个能表示实际问题意义的不等关系
4.列不等式
5.解不等式,并检验答案是否符合题意
6.答 注意:根据题目实际有时需选取整数解
3.设未知数
注意:
设不写“最多”、“至少”……
学习目标
能够找出问题中的不等关系并列出一元一次不等式解决简单的实际问题.
学习目标
难点
寻找实际问题中的不等关系,建立数学模型。
1.某工程队计划在10天整修河堤600m.施工2天修了120m后,该工程需要比原计划提前2天完成,此后平均每天至少要整修河堤多少米?
限时任务题型
题型分析:
1、题中含有不等关系的语句_____________________________________。
2、将不等关系转化为不等式,即_________________________________。
3、假设此后平均每天要整修河堤x米,根据题干内容,实际工期为_______________天。
该工程需要比原计划提前2天完成
实际工期≤原计划工期-2
2+(600-120)/x
4.我们需要对限时任务题目重新理解:_________________________________。
2天的完成量+剩下6天的可完成量≥600m
注意:分母出现未知数!
改变思路:
求出工作量!
1.某工程队计划在10天整修河堤600m.施工2天修了120m后,该工程需要比原计划提前2天完成,此后平均每天至少要整修河堤多少米?
限时任务题型巩固
题型分析:
1、题中含有不等关系的语句_____________________________________。
2、将不等关系转化为不等式,即_________________________________。
3、设此后平均每天要整修河堤x米,不等式方程为_____________________
解得x≥80
该工程需要比原计划提前2天完成
2天的完成量+剩下6天的可完成量≥600m
120+(10-2-2)x≥600
用文字形式
建立不等式模型
情景引入
1. 某人骑一辆变速自行车,如果行驶增加4km/h,那么2h所行驶的路程不少于以原来速度2.5h所行驶的路程.原来行驶的速度最大是多少?
分析:
1、题中含有不等关系的语句_____________________________________。
2、将不等关系转化为不等式,即_________________________________。
3、假设原来行驶的速度为x km/h,根据题干内容,提速后的速度为_______________。
4、不等式方程为______
2h所行驶的路程不少于以原来速度2.5h所行驶的路程
x+4
2h所行驶的路程>原来速度2.5h所行驶的路程
2(x+4)≥2.5x
限时任务题型:
1.时间是有限制要求
2.已完成量(路程)+剩余时间内按效率/速度预算的量(路程) ≥ (或>) 计划量(路程)
3.剩余时间内按效率/速度预算的量(路程)是未发生,不确定的
2.某车间计划在15天内至少加工零件408个,前3天每天加工零件24个。此后,该车工平均每天至少需要加工零件多少个,才能在规定时间内完成任务?
限时任务题型巩固
题型分析:
1、题中含有不等关系的语句_____________________________________。
2、将不等关系转化为不等式,即_________________________________。
3、设平均每天需要加工零件x个,不等式方程为__________________
解得x≥28
15天内至少加工零件408个
前三天完成量+剩余时间完成量≥408个
24×3+(15-3)x≥408
3.某工地要实施爆破,导火线的燃烧速度是0.8cm/s,引爆人在点燃导火线后要跑到200m以外的安全区域.如果引爆人跑步的速度是5m/s,那么导火线的长度应大于多少?
3.某工地要实施爆破,导火线的燃烧速度是0.8cm/s,引爆人在点燃导火线后要跑到200m以外的安全区域.如果引爆人跑步的速度是5m/s,那么导火线的长度应大于多少?
限时任务题型巩固-限时逃脱
题型分析:
1、题中含有不等关系的语句_____________________________________。
2、将不等关系转化为不等式,即_________________________________。
3、设导火线的长度为x cm,不等式方程为__________________
点燃导火线后要跑到200m以外的安全区域
爆炸前跑出的路程>200m
解得x>32
单位统一问题:保证同级别的运算 单位统一即可
情景引入
1. 某人骑一辆变速自行车,如果行驶增加4km/h,那么2h所行驶的路程不少于以原来速度2.5h所行驶的路程.原来行驶的速度最大是多少?
分析:
1、题中含有不等关系的语句_____________________________________。
2、将不等关系转化为不等式,即_________________________________。
3、假设原来行驶的速度为x km/h,根据题干内容,提速后的速度为_______________。
4、不等式方程为______
2h所行驶的路程不少于以原来速度2.5h所行驶的路程
x+4
2h所行驶的路程>原来速度2.5h所行驶的路程
2(x+4)≥2.5x
关于折扣:
打几折:售价是标价的百分之几十
打几几折:售价是标价的百分之几十几。
对客户而言,折扣是打得越多越好,因为售价会越便宜。
售价=标价(不变)×折扣比率,对应的折扣比率(若设为x,x<1)就越小;
反过来,对商家来说折扣过多,有亏本的风险 ,一般说“最多打几折销售”
4.某超市进了某种糖果 1000kg,进价是7元/kg,售价定为10元/kg,销售一半以后,为了尽快售完,准备打折出售。如果要使总利润不低于2000元,那么余下的糖果可以按原定价最多打几折出售?
保证利润题型
题型分析:
1、题中含有不等关系的语句_____________________________________。
2、将不等关系转化为不等式,即_________________________________。
3、设折扣比率为x,不等式方程为__________________________________________
解得x≥80%
总利润不低于2000元
第一次销售额+第二次销售额-进价≥2000元
(1000×0.5)×10+(1000×0.5)×10x-1000×7≥2000
相关公式:标价*折扣比例=售价
售价-进价=利润
情景引入
1. 某人骑一辆变速自行车,如果行驶增加4km/h,那么2h所行驶的路程不少于以原来速度2.5h所行驶的路程.原来行驶的速度最大是多少?
分析:
1、题中含有不等关系的语句_____________________________________。
2、将不等关系转化为不等式,即_________________________________。
3、假设原来行驶的速度为x km/h,根据题干内容,提速后的速度为_______________。
4、不等式方程为______
2h所行驶的路程不少于以原来速度2.5h所行驶的路程
x+4
2h所行驶的路程>原来速度2.5h所行驶的路程
2(x+4)≥2.5x
保证利润题型:
1.保证利润:利润不低于,利润率不低于
2. 解题思路:总售价-总成本≥预期的利润额
3. 利润额=成本×利润率
4.成本控制:总成本是低于或不高于某一金额
5.解题思路:各项成本之和<控制成本
5.某商品的成本为2000元,标价为2800元,如果商店要以利润不低于5%的价格销售,那么最低可以打几折出售这些商品?
保证利润题型巩固
题型分析:
1、题中含有不等关系的语句_____________________________________。
2、将不等关系转化为不等式,即_________________________________。
3、假设折扣比率为x,不等式方程为__________________
解得x≥75%
利润不低于5%
售价-成本≥5%的利润额
2800x-2000≥2000×5%
相关公式:标价*折扣比例=售价 售价-成本=利润
利润=成本×利润率(百分比)
售价-进价=利润
6.某房地产开发商用2600万元购买了一块地用于建造居民住宅楼,如住宅楼每平米的造价约为1400元,那么建筑面积必须超过多少平方米才能将建楼成本控制在每平米4000元以下?
6.某房地产开发商用2600万元购买了一块地用于建造居民住宅楼,如住宅楼每平米的造价约为1400元,那么建筑面积必须超过多少平方米才能将建楼成本控制在每平米4000元以下?
保证利润-成本控制题型巩固
保证利润题型分析:
1、题中含有不等关系的语句_____________________________________。
2、将不等关系转化为不等式,即_________________________________。
3、假设建筑面积为x平方米,根据题干内容,___________________________。
4、不等式方程为__________________
解得x>10000
建楼成本控制在每平米4000元以下
建楼每平方米成本=(26000000+1400x)/x
建楼每平方米成本<4000元
26000000+1400x<4000x
注意:分母出现未知数!
地价+实际造价<4000元单价对应的建楼成本(控制成本)
地价+实际造价=26000000+1400x
关键:
与控制成本比较!
A.计算题解的检验
1.不等式计算题中,如
解:
1.上一题解得 x>10000
问题:“建筑面积必须超过多少平方米”
出现“超过”,建筑面积的解集
应带“>”“≥”
去分母 2(-2x+1)≥-x+8去括号 -4x+2≥-x+8
移项 -4x+x≥+8-2
合并同类项 -3x≥6
系数化为1 x≤-2
B.应用题解的检验
2.检验解集不等号:检查倒数第二行 -3x≥6 未知数系数是负数,所以符号改变是正确的
3. 检验解集数字:将x=-2代入 左边=右边,所以数字也是正确的
2.总结: 根据最后问题验证解集的符号
①含有大于、超过、至少、最少、最低 、最小,解集应带“>”“≥”
②含有小于、至多、最多、最高 、最大,
解集应带“<”“≤”
例外: “打折”
课后回顾
寻找实际问题中的不等关系
01
课后回顾
建立数学模型
02
利用解不等式
解决简单实际问题
03
8.某童装店按每套90元的价格购进40套童装,应缴纳的税费为销售额的10%. 如果要获得不低于900元的纯利润,每套童装的售价至少是多少元?
练习巩固:
7.甲、乙两地相距100km,一批物资需要在1h内从甲地送到乙地。某人驾驶汽车,前半小时走了40km,后半小时的速度至少为多少才能保证这批物资及时送到?
THE END
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
