2020-2021学年苏科版七年级数学下册11.5用一元一次不等式解决问题-专题复习提升训练(word含答案)
文档属性
| 名称 | 2020-2021学年苏科版七年级数学下册11.5用一元一次不等式解决问题-专题复习提升训练(word含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 384.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-06 21:15:34 | ||
图片预览




文档简介
专题复习提升训练卷11.5用一元一次不等式解决问题-20-21苏科版七年级数学下册
一、选择题
1、一次生活常识知识竞赛一共有30道题,答对一题得4分,不答得0分,答错扣2分.小聪有2道题没答,竞赛成绩超过80分,则小聪至多答错了________道题.
2、在抗震救灾中,某抢险地段需实行爆破.操作人员点燃导火线后,要在炸药爆炸前跑到以外的安全区域.已知导火线的燃烧速度是,操作人员跑步的速度是6m/s.为了保证操作人员的安全,导火线的长度要超过( )
A. B. C. D.
3、小明要从甲地到乙地,两地相距1.8千米.已知他步行的平均速度为90米/分,跑步的平均速度为210米/分,若他要在不超过15分钟的时间内从甲地到达乙地,至少需要跑步多少分钟?设他需要跑步x分钟,则列出的不等式为( )
A.210x+90(15﹣x)≥1.8 B.90x+210(15﹣x)≤1800
C.210x+90(15﹣x)≥1800 D.90x+210(15﹣x)≤1.8
4、某城市的一种出租车起步价是7元(即在3km以内的都付7元车费),超过3km后,每增加1km加价1.2元(不足1km按1km计算),现某人付了14.2元车费,求这人乘的最大路程是( )
A.10km B.9 km C.8km D.7 km
5、某电信公司推出两种手机收费方案.方案A:月租费30元,本地通话话费0.15元/分;方案B:不收月租费,本地通话话费为0.3元/分.设婷婷的爸爸一个月通话时间为x分钟,婷婷的爸爸一个月通话时间为多少时,选择方案A比方案B优惠?( )
A.100分钟 B.150分钟 C.200分钟 D.250分钟
6、阿慧在店内购买两种蛋糕当伴手礼,如图为蛋糕的价目表.已知阿慧共购买盒蛋糕,花费的金额不超过元.若他将蛋糕分给位同事,每人至少能拿到一个蛋糕,则阿慧花多少元购买蛋糕?( )
A. B. C. D.
7、某种商品的进价为500元,出售时标价为750元,由于换季,商店准备打折销售,但要保持利润不低于20%,那么至多打( )
A.6折 B.7折 C.8折 D.9折
8、小聪去商店购买笔记本和钢笔,共用了60元钱,已知每本笔记本2元,每支钢笔5元,若笔记本和钢笔都需购买,且笔记本的数量多于钢笔的数量,则小聪的购买方案有( )
A.3种 B.4种 C.5种 D.6种
9、小明去商店购买A、B两种玩具,共用了10元钱,A种玩具每件1元,B种玩具每件2元.若每种玩具至少买一件,且A种玩具的数量多于B种玩具的数量.则小明的购买方案有( )
A.5种 B.4种 C.3种 D.2种
10、运行程序如图所示,规定:从“输入一个值x”到“结果是否>26”为一次程序操作,如果程序操作进行
了2次后停止,那么满足条件的所有整数x的和为( )
A.30 B.35 C.42 D.39
二、填空题
11、某商场推出一种购物金卡,凭卡在该商场购物可按商品价格的九折付款,但办理金卡时每张要收50元购卡费,设按标价累计购物金额为x(元),当 时,办理金卡购物省钱.?
12、有10名菜农,每人可种甲种蔬菜3亩或乙种蔬菜2亩,已知甲种蔬菜每亩可收入0.5万元,乙种蔬菜每亩可收入0.8万元,若要使总收入不低于15.6万元,则最多能安排 人种甲种蔬菜.?
13、有学生若干人,住若干间宿舍,若每间住5人,则有14人无法安排住宿,若每间住8人,则最后有一间宿舍不满也不空,则学生人数为_____.
14、某种型号汽车每行驶100km耗油10L,其油箱容量为40L.为了有效延长汽车使用寿命,厂家建议每次加油时邮箱内剩余油量不低于油箱容量的,按此建议,一辆加满油的该型号汽车最多行驶的路程是_____km.
15、甲乙两队进行篮球对抗赛,比赛规则规定每队胜一场得3分,平一场得1分,负一场得0分,两队一共比赛了10场,甲队保持不败,得分不低于24分,甲队至少胜了___________场.
16、某种商品的进价为15元,出售时标价是22.5元.由于市场不景气销售情况不好,商店准备降价处理,但要保证利润率不低于10%,那么该店最多降价______元出售该商品.
17、一次生活常识知识竞赛一共有20道题,答对一题得5分,不答得0分,答错扣2分,小聪有1道题没答,竞赛成绩超过80分,则小聪至少答对了_______道题.
18、疫情过后,地摊经济火爆,张阿姨以每件80元的价格购进50件衬衫,在地摊上以每件100元的价格出售,她至少销售__________件衬衫,所得销售额才能超过进货总价.
19、“一方有难,八方支援”.某学校计划购买84消毒液和75%酒精消毒水共4000瓶,用于支援武汉抗击“新冠肺炎疫情”.已知84消毒液的单价为3元/瓶,75%酒精消毒水的单价为13元/瓶,若购买这批物资的总费用不超过28000元,则至少需要购买84消毒液多少瓶?
20、4月21日是重庆一中校庆日,学校每一年都要举行校庆活动和教职工运动会,全校分校区或年级组队进行角逐,今年某校区给参赛老师购买了、、三种运动服,每一套价格分别是400元,500元,600元,其中种运动服套数是种运动服套数的3倍,种运动服套数比C种运动服套数的2倍还多,要求购买服装的总套数尽量多且总费用不超过52300元,则能购买到运动服最多_________套.
三、解答题
21、一工厂以90元/每箱的价格购进100箱原材料,准备由甲、乙两个车间全部用于生产某种产品,甲车间用每箱原材料可生产出该产品12千克,乙车间用每箱原材料可生产出的该产品比甲车间少2千克,已知该产品的售价为40元/千克,生产的产品全部售出,那么原材料最少分配给甲车间多少箱,才能使去除成本后所获得的总利润不少于35000元?
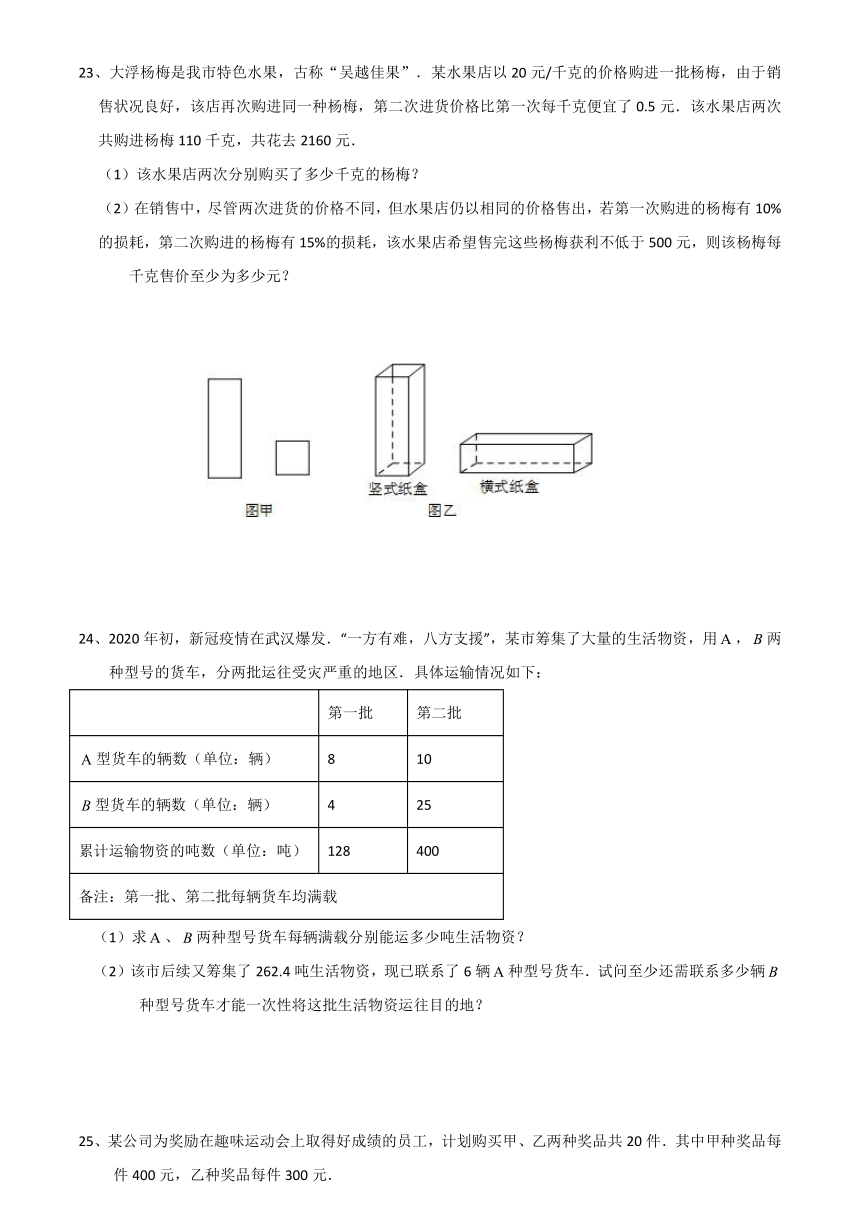
22、某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方形形状的
无盖纸盒.
(1)现有正方形纸板150张,长方形纸板300张,若这些纸板恰好用完,则可制作横式、竖式两种纸盒各多少个?
(2)若有正方形纸板32张,长方形纸板张,做成上述两种纸盒,纸板恰好用完,已知.
求的值.
23、大浮杨梅是我市特色水果,古称“吴越佳果”.某水果店以20元/千克的价格购进一批杨梅,由于销售状况良好,该店再次购进同一种杨梅,第二次进货价格比第一次每千克便宜了0.5元.该水果店两次共购进杨梅110千克,共花去2160元.
(1)该水果店两次分别购买了多少千克的杨梅?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的杨梅有10%
的损耗,第二次购进的杨梅有15%的损耗,该水果店希望售完这些杨梅获利不低于500元,则该杨梅每千克售价至少为多少元?
24、2020年初,新冠疫情在武汉爆发.“一方有难,八方支援”,某市筹集了大量的生活物资,用,两种型号的货车,分两批运往受灾严重的地区.具体运输情况如下:
第一批 第二批
型货车的辆数(单位:辆) 8 10
型货车的辆数(单位:辆) 4 25
累计运输物资的吨数(单位:吨) 128 400
备注:第一批、第二批每辆货车均满载
(1)求、两种型号货车每辆满载分别能运多少吨生活物资?
(2)该市后续又筹集了262.4吨生活物资,现已联系了6辆种型号货车.试问至少还需联系多少辆 种型号货车才能一次性将这批生活物资运往目的地?
25、某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件.其中甲种奖品每件400元,乙种奖品每件300元.
(1)如果购买甲、乙两种奖品共花费了6500元,求甲、乙两种奖品各购买了多少件;
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过6800元,求该公司有哪几种不同的购买方案.
26、某学校为了增强学生体质,加强体育锻炼,决定让各班购买跳绳和毽子作为活动器材.已知购买2根跳绳和5个毽子共需32元;购买4根跳绳和3个毽子共需36元.
(1)求购买一根跳绳和一个毽子分别需要多少元;
(2)某班需要购买跳绳和毽子的总数量是54,且购买的总费用不能超过260元;若要求购买跳绳的数量多于20根,通过计算说明共有哪几种购买方案.
27、为应对新冠肺炎疫情,某服装厂决定转型生产口罩,根据现有厂房大小决定购买10条口罩生产线,现有甲、乙两种型号的口罩生产线可供选择.经调查:购买3台甲型口罩生产线比购买2台乙型口罩生产线多花14万元,购买4条甲型口罩生产线与购买5条乙型口罩生产线所需款数相同.
(1)求甲、乙两种型号口罩生产线的单价;
(2)已知甲型口罩生产线每天可生产口罩9万只,乙型口罩生产线每天可生产口罩7万只,若每天要求产量不低于75万只,预算购买口罩生产线的资金不超过90万元,该厂有哪几种购买方案?哪种方案最省钱?最少费用是多少?
专题复习提升训练卷11.5用一元一次不等式解决问题-20-21苏科版七年级数学下册(解析)
一、选择题
1、一次生活常识知识竞赛一共有30道题,答对一题得4分,不答得0分,答错扣2分.小聪有2道题没答,竞赛成绩超过80分,则小聪至多答错了________道题.
【答案】5
【分析】设小聪答错了x道题,则答对了(30-x-2)道题,根据总分=5×答对题目数-2×答错题目数结合总分超过80分,即可得出关于x的一元一4,则答对了(30-x-2)道题,
依题意得:,解得:,
∵错题数为整数,∴x最大值为5,故答案为:5.
2、在抗震救灾中,某抢险地段需实行爆破.操作人员点燃导火线后,要在炸药爆炸前跑到以外的安全区域.已知导火线的燃烧速度是,操作人员跑步的速度是6m/s.为了保证操作人员的安全,导火线的长度要超过( )
A. B. C. D.
【答案】A
【分析】根据题意可知:操作人员点燃导火线后,要在炸药爆炸前跑到450米以外的安全区域,列出不等式,解不等式即可.
【详解】解:设导火线长度为xcm,根据题意得, >,
解得x>90,
故选:A.
3、小明要从甲地到乙地,两地相距1.8千米.已知他步行的平均速度为90米/分,跑步的平均速度为210米/分,若他要在不超过15分钟的时间内从甲地到达乙地,至少需要跑步多少分钟?设他需要跑步x分钟,则列出的不等式为( )
A.210x+90(15﹣x)≥1.8 B.90x+210(15﹣x)≤1800
C.210x+90(15﹣x)≥1800 D.90x+210(15﹣x)≤1.8
【答案】C
【分析】根据题意,利用要在不超过15分钟的时间内从甲地到达乙地建立不等式即可解题.
【详解】解:由题可知只需要小明在15分钟之内走过的路程大于1800即可,
即210x+90(15﹣x)≥1800
故选C.
4、某城市的一种出租车起步价是7元(即在3km以内的都付7元车费),超过3km后,每增加1km加价1.2元(不足1km按1km计算),现某人付了14.2元车费,求这人乘的最大路程是( )
A.10km B.9 km C.8km D.7 km
【答案】B
【分析】设路程为x千米,依题意得13<7+1.2(x-3)≤14.2,解不等式即可.注意考虑到不足1千米也按1千米收费.
【详解】解:设路程为x千米,
依题意得13<7+1.2(x-3)≤14.2,
解得8<x≤9,
故这人乘的最大路程是9km,
故选:B
5、某电信公司推出两种手机收费方案.方案A:月租费30元,本地通话话费0.15元/分;方案B:不收月租费,本地通话话费为0.3元/分.设婷婷的爸爸一个月通话时间为x分钟,婷婷的爸爸一个月通话时间为多少时,选择方案A比方案B优惠?( )
A.100分钟 B.150分钟 C.200分钟 D.250分钟
【答案】D
【分析】由题意易得,然后进行求解排除选项即可.
【详解】解:设婷婷的爸爸一个月通话时间为x分钟,由题意得:,
解得:,∴只有D选项符合题意;故选D.
6、阿慧在店内购买两种蛋糕当伴手礼,如图为蛋糕的价目表.已知阿慧共购买盒蛋糕,花费的金额不超过元.若他将蛋糕分给位同事,每人至少能拿到一个蛋糕,则阿慧花多少元购买蛋糕?( )
A. B. C. D.
【答案】D
【分析】可设阿慧购买x盒桂圆蛋糕,则购买(10-x)盒金枣蛋糕,根据不等关系:①购买10盒蛋糕,花费的金额不超过500元;②蛋糕的个数大于等于75个,列出不等式组求解即可.
【详解】解:设阿慧购买x盒桂圆蛋糕,则购买(10-x)盒金枣蛋糕,依题意有
,解得≤x≤,
∵x是整数,∴x=3,
70×3+40×(10-3)=490(元).
答:阿慧花490元购买蛋糕. 故选:D.
7、某种商品的进价为500元,出售时标价为750元,由于换季,商店准备打折销售,但要保持利润不低于20%,那么至多打( )
A.6折 B.7折 C.8折 D.9折
【答案】C
【分析】设该服装打x折销售,根据利润=售价-进价结合利润不低于20%,即可得出关于x的一元一次不
等式,解之取其中的最小值即可得出结论.
【详解】解:设该服装打x折销售,
依题意,得: ,
解得:x≥8.
故选:C.
8、小聪去商店购买笔记本和钢笔,共用了60元钱,已知每本笔记本2元,每支钢笔5元,若笔记本和钢笔都需购买,且笔记本的数量多于钢笔的数量,则小聪的购买方案有( )
A.3种 B.4种 C.5种 D.6种
【答案】B
【分析】设笔记本的数量为x个,钢笔的数量为y个,用笔记本的钱数+钢笔的钱数=60,笔记本数量>钢笔数量,可以列出一元一次不等式,求出其解集,再根据笔记本数,钢笔数必须是整数,确定购买方案.
【详解】(1)设笔记本的数量为x个,钢笔的数量为y个.
由题意得:,
∴,, 解得:.
∵为正整数,∴x为5的倍数,故x的取值为10,15,20,25.
故有四种方案.
故选B.
9、小明去商店购买A、B两种玩具,共用了10元钱,A种玩具每件1元,B种玩具每件2元.若每种玩具至少买一件,且A种玩具的数量多于B种玩具的数量.则小明的购买方案有( )
A.5种 B.4种 C.3种 D.2种
【分析】设小明购买了A种玩具x件,则购买的B种玩具为件,根据题意列出不等式组进行解答便可.
【解析】:设小明购买了A种玩具x件,则购买的B种玩具为件,根据题意得,
,解得,3∵x为整数,也为整数,
∴x=4或6或8,
∴有3种购买方案.
故选:C.
10、运行程序如图所示,规定:从“输入一个值x”到“结果是否>26”为一次程序操作,如果程序操作进行
了2次后停止,那么满足条件的所有整数x的和为( )
A.30 B.35 C.42 D.39
【答案】D
【提示】根据题意可知第一次所得的结果≤26,第二次所得的结果>26,列不等式组并解除不等式组得解后再计算满足条件的所有整数的和即可.
【详解】由题意得,
解不等式①得,x≤9,
解不等式②得,x>,
∴x的取值范围是<x≤9,
∴满足条件的所有整数x的和为4+5+6+7+8+9=39.
故答案选D.
二、填空题
11、某商场推出一种购物金卡,凭卡在该商场购物可按商品价格的九折付款,但办理金卡时每张要收50元购卡费,设按标价累计购物金额为x(元),当 时,办理金卡购物省钱.?
[答案] 500
[解析] 根据题意,得x-0.9x>50,解得x>500,即当购物金额大于500元时,办理金卡购物省钱.
12、有10名菜农,每人可种甲种蔬菜3亩或乙种蔬菜2亩,已知甲种蔬菜每亩可收入0.5万元,乙种蔬菜每亩可收入0.8万元,若要使总收入不低于15.6万元,则最多能安排 人种甲种蔬菜.?
[答案] 4
[解析] 设安排x人种甲种蔬菜,则3x×0.5+2(10-x)×0.8≥15.6,解得x≤4,
所以最多能安排4人种甲种蔬菜.
13、有学生若干人,住若干间宿舍,若每间住5人,则有14人无法安排住宿,若每间住8人,则最后有一间宿舍不满也不空,则学生人数为_____.
【答案】39或44或49
【分析】设共有x间宿舍,则学生数有(5x+14)人,列出不等式组为0<5x+14?8(x?1)<8解出即可.
【详解】设共有x间宿舍,则学生数有(5x+14)人,
根据题意得:0<5x+14?8(x?1)<8,解得<x<,
∵x为整数,∴x=5或6或7,即学生有5x+14=39或5x+14=44或5x+14=49.
即,学生人数是39或44人或49;故答案为:39或44或49.
14、某种型号汽车每行驶100km耗油10L,其油箱容量为40L.为了有效延长汽车使用寿命,厂家建议每次加油时邮箱内剩余油量不低于油箱容量的,按此建议,一辆加满油的该型号汽车最多行驶的路程是_____km.
【答案】350.
【提示】设行驶xkm,由油箱内剩余油量不低于油箱容量的,列出不等式,即可求解.
【详解】设该型号汽车行驶的路程是xkm,
∵油箱内剩余油量不低于油箱容量的,
∴﹣x+40≥40×,解得:x≤350,
答:该辆汽车最多行驶的路程是350km,
故答案为:350.
15、甲乙两队进行篮球对抗赛,比赛规则规定每队胜一场得3分,平一场得1分,负一场得0分,两队一共比赛了10场,甲队保持不败,得分不低于24分,甲队至少胜了___________场.
【答案】7
【分析】设甲队胜了x场,则平了(10-x)场,根据胜一场得3分,平一场得1分,负一场得0分,比赛10场,得分24分,列出不等式,求出x的最小整数解.
【详解】设甲队胜了x场,则平了(10-x)场,
由题意得,3x+(10-x)≥24,解得:x≥7,即甲队至少胜了7场.故答案是:7.
16、某种商品的进价为15元,出售时标价是22.5元.由于市场不景气销售情况不好,商店准备降价处理,但要保证利润率不低于10%,那么该店最多降价______元出售该商品.
【答案】6
【解析】先设最多降价x元出售该商品,则出售的价格是22.5-x-15元,再根据利润率不低于10%,列出不等式即可.
解:设最多降价x元出售该商品,则22.5-x-15≥15×10%,解得x≤6.
故该店最多降价6元出售该商品.
17、一次生活常识知识竞赛一共有20道题,答对一题得5分,不答得0分,答错扣2分,小聪有1道题没答,竞赛成绩超过80分,则小聪至少答对了_______道题.
【答案】17
【分析】设小聪答对了x道题,根据“答对题数×5?答错题数×2>80分”列出不等式,解之可得.
【详解】设小聪答对了x道题,根据题意,得:5x?2(19?x)>80,解得x>16,
∵x为整数,∴x=17,即小聪至少答对了17道题,故答案为:17.
18、疫情过后,地摊经济火爆,张阿姨以每件80元的价格购进50件衬衫,在地摊上以每件100元的价格出售,她至少销售__________件衬衫,所得销售额才能超过进货总价.
【答案】41
【提示】根据题意,可以设销售x件衬衫,然后列出不等式100x>80×50,求出x的取值范围,注意x为整数,从而可以得到x的最小整数值,本题得以解决.
【详解】解:设销售x件衬衫,依题意有100x>80×50,
解得x>40,
∵x为整数,
∴x最小是41.
答:她至少销售41件衬衫,所得销售额才能超过进货总价.
故答案为:41.
19、“一方有难,八方支援”.某学校计划购买84消毒液和75%酒精消毒水共4000瓶,用于支援武汉抗击“新冠肺炎疫情”.已知84消毒液的单价为3元/瓶,75%酒精消毒水的单价为13元/瓶,若购买这批物资的总费用不超过28000元,则至少需要购买84消毒液多少瓶?
解:设需要购买84消毒液x瓶,则购买75%酒精消毒水(4000-x)瓶.依题意,得
3x+13(4000-x)≤28000,
解得x≥2400.
答:至少需要购买84消毒液2400瓶.
20、4月21日是重庆一中校庆日,学校每一年都要举行校庆活动和教职工运动会,全校分校区或年级组队进行角逐,今年某校区给参赛老师购买了、、三种运动服,每一套价格分别是400元,500元,600元,其中种运动服套数是种运动服套数的3倍,种运动服套数比C种运动服套数的2倍还多,要求购买服装的总套数尽量多且总费用不超过52300元,则能购买到运动服最多_________套.
【答案】111
【分析】设C种运动服购买x套,则A种运动服3x套,B种运动服的套数大于2x,由题意列不等式,结合问题的实际意义,且x必须取整可解.
【详解】设C种运动服购买x套,则A种运动服3x套,B种运动服的套数大于2x,由题意得
52300?600x?400×3x>500×2x, ∴52300>2800x
∴x<, ∴2x<
∵x必须为正整数, ∴x的最大值为18
∴应购买A种运动服54套,购买C种运动服18套,
∵(52300?400×54?600×18)÷500=39.8
购买B种运动服39套,
最多能购买54+39+18=111套.
故答案为:111
三、解答题
21、一工厂以90元/每箱的价格购进100箱原材料,准备由甲、乙两个车间全部用于生产某种产品,甲车间用每箱原材料可生产出该产品12千克,乙车间用每箱原材料可生产出的该产品比甲车间少2千克,已知该产品的售价为40元/千克,生产的产品全部售出,那么原材料最少分配给甲车间多少箱,才能使去除成本后所获得的总利润不少于35000元?
【分析】设甲车间用x箱原材料,则乙车间用(100﹣x)箱原材料,根据题意列出不等式,
【解答】解:设甲车间用x箱原材料,则乙车间用(100﹣x)箱原材料,
根据题意,得12x×40+(100﹣x)(12﹣2)×40﹣100×90≥35000.
解得x≥50.
答:原材料最少分配给甲车间50箱,才能使去除成本后所获得的总利润不少于35000元.
22、某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方形形状的
无盖纸盒.
(1)现有正方形纸板150张,长方形纸板300张,若这些纸板恰好用完,则可制作横式、竖式两种纸盒各多少个?
(2)若有正方形纸板32张,长方形纸板张,做成上述两种纸盒,纸板恰好用完,已知.
求的值.
【答案】(1);(2)a=73
【分析】(1)设制作竖式纸盒x个,则制作横式纸盒y个.根据制作竖式纸盒用的正方形纸板+制作横式纸盒用的正方形纸板=150张;制作竖式纸盒用的长方形纸板+制作横式纸盒用的长方形纸板=300张.列方程组即可得到结论;
(2)设x个竖式需要正方形纸板x张,长方形纸板横4x张;y个横式需要正方形纸板2y张,长方形纸板横3y张,可列出方程组,再根据a的取值范围求出y的取值范围即可.
【详解】解:(1)设制作竖式纸盒x个,则制作横式纸盒y个.
由题意得,解得:,
答:可制作横式纸盒60个、竖式纸盒30个;
(2)设制作竖式纸盒x个,则制作横式纸盒y个.由题意得,解得y=,
∵70<a<75,∴53<128-a<58,
∵y是整数,∴128-a=55,∴a=73.
23、大浮杨梅是我市特色水果,古称“吴越佳果”.某水果店以20元/千克的价格购进一批杨梅,由于销售状况良好,该店再次购进同一种杨梅,第二次进货价格比第一次每千克便宜了0.5元.该水果店两次共购进杨梅110千克,共花去2160元.
(1)该水果店两次分别购买了多少千克的杨梅?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的杨梅有10%的损耗,第二次购进的杨梅有15%的损耗,该水果店希望售完这些杨梅获利不低于500元,则该杨梅每千克售价至少为多少元?
【分析】(1)设该水果店两次分别购买了x元和y元的水果.根据“购进同一种水果,第二次进货价格比第一次每千克便宜了0.5元,该水果店两次共购进杨梅110千克,”、“两次购进水果共花去了2160元”列出方程组并解答;
(2)设该水果每千克售价为m元,则由“售完这些水果获利不低于500元”列出不等式并解答.
【解析】(1)设该水果店两次分别购买了x元和y元的水果.根据题意,得
解得:x=30,y=80,
答:水果店两次分别购买了30千克和80千克的杨梅;
(2)设该杨梅每千克售价为m元,根据题意,得:
m[30(1﹣10%)+80(1﹣15%)]﹣2160≥500,
解得:m≥28,
答:该杨梅每千克售价至少为28元.
24、2020年初,新冠疫情在武汉爆发.“一方有难,八方支援”,某市筹集了大量的生活物资,用,两种型号的货车,分两批运往受灾严重的地区.具体运输情况如下:
第一批 第二批
型货车的辆数(单位:辆) 8 10
型货车的辆数(单位:辆) 4 25
累计运输物资的吨数(单位:吨) 128 400
备注:第一批、第二批每辆货车均满载
(1)求、两种型号货车每辆满载分别能运多少吨生活物资?
(2)该市后续又筹集了262.4吨生活物资,现已联系了6辆种型号货车.试问至少还需联系多少辆 种型号货车才能一次性将这批生活物资运往目的地?
【答案】(1)A:10吨,B:12吨;(2)至少需要B型17辆
【分析】
(1)设A,B两种型号货车每辆满载分别能运x,y吨生活物资,根据条件建立方程组求出其解即可;
(2)设还需联系m辆B型号货车才能一次性将这批生活物资运往目的地,根据题中的不等关系列出不等式解答即可.
【详解】(1)设A,B两种型号货车每辆满载分别能运x,y吨生活物资
依题意,得解得
∴A,B两种型号货车每辆满载分别能运10吨,12吨生活物资
(2)设还需联系m辆B型号货车才能一次性将这批生活物资运往目的地
依题意,得.
解得
又m为整数,
∴m最小取17,
∴至少还需联系17辆B型号货车才能一次性将这批生活物资运往目的地.
25、某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件.其中甲种奖品每件400元,乙种奖品每件300元.
(1)如果购买甲、乙两种奖品共花费了6500元,求甲、乙两种奖品各购买了多少件;
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过6800元,求该公司有哪几种不同的购买方案.
【分析】(1)设甲种奖品购买了a件,乙种奖品购买了(20﹣a)件,利用购买甲、乙两种奖品共花费了6500元列方程400a+300(20﹣a)=6500,然后解方程求出a,再计算20﹣a即可;
(2)设甲种奖品购买了x件,乙种奖品购买了(20﹣x)件,利用购买乙种奖品的件数不超过甲种
奖品件数的2倍,总花费不超过680元列不等式组,然后解不等式组后确定x的整数值即可得到该公司的购买方案.
【解析】(1)设甲种奖品购买了a件,乙种奖品购买了(20﹣a)件,
根据题意得400a+300(20﹣a)=6500,解得a=5,
则20﹣a=15,
答:甲种奖品购买了5件,乙种奖品购买了15件;
(2)设甲种奖品购买了x件,乙种奖品购买了(20﹣x)件,
根据题意得,解得x≤8,
∵x为整数,∴x=7或x=8,
当x=7时,20﹣x=13;当x=8时,20﹣x=12;
答:该公司有2种不同的购买方案:
甲种奖品购买了:7件,乙种奖品购买了13件
或甲种奖品购买了8件,乙种奖品购买了12件.
26、某学校为了增强学生体质,加强体育锻炼,决定让各班购买跳绳和毽子作为活动器材.已知购买2根跳绳和5个毽子共需32元;购买4根跳绳和3个毽子共需36元.
(1)求购买一根跳绳和一个毽子分别需要多少元;
(2)某班需要购买跳绳和毽子的总数量是54,且购买的总费用不能超过260元;若要求购买跳绳的数量多于20根,通过计算说明共有哪几种购买方案.
【答案】(1)购买一根跳绳需要6元,购买一个毽子需要4元;
(2)共有2种购买方案,方案1:购买21根跳绳,33个毽子;方案2:购买22根跳绳,32个毽子.
【分析】(1)设购买一根跳绳需要x元,购买一个毽子需要y元,根据“购买2根跳绳和5个毽子共需32元;购买4根跳绳和3个毽子共需36元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购买m根跳绳,则购买(54?m)个毽子,根据购买的总费用不能超过260元且购买跳绳的数量多于20根,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,结合m为正整数即可得出各购买方案.
【详解】解:(1)设购买一根跳绳需要x元,购买一个毽子需要y元,
依题意,得:,解得:.
答:购买一根跳绳需要6元,购买一个毽子需要4元;
(2)设购买m根跳绳,则购买(54?m)个毽子,
依题意,得:,解得:20<m≤22.
又∵m为正整数,∴m可以为21,22.
∴共有2种购买方案,
方案1:购买21根跳绳,33个毽子;
方案2:购买22根跳绳,32个毽子.
27、为应对新冠肺炎疫情,某服装厂决定转型生产口罩,根据现有厂房大小决定购买10条口罩生产线,现有甲、乙两种型号的口罩生产线可供选择.经调查:购买3台甲型口罩生产线比购买2台乙型口罩生产线多花14万元,购买4条甲型口罩生产线与购买5条乙型口罩生产线所需款数相同.
(1)求甲、乙两种型号口罩生产线的单价;
(2)已知甲型口罩生产线每天可生产口罩9万只,乙型口罩生产线每天可生产口罩7万只,若每天要求产量不低于75万只,预算购买口罩生产线的资金不超过90万元,该厂有哪几种购买方案?哪种方案最省钱?最少费用是多少?
【分析】(1)设未知数,列二元一次方程组可以求解,
(2)设购买甲设备a台,根据购买甲型设备不少于3台,和购买甲、乙两种新设备的资金不超过110万元,列出不等式组,根据不等式组的整数解得出购买方案.
【解析】(1)设甲型号口罩生产线的单价为x万元,乙型号口罩生产线的单价为y万元,由题意得:
, 解得:,
答:甲型号口罩生产线的单价为10万元,乙型号口罩生产线的单价为8万元.
(2)设购买甲型号口罩生产线m条,则购买乙型号口罩生产线(10﹣m)条,由题意得:
, 解得:2.5≤m≤5,
又∵m为整数,∴m=3,或m=4,或m=5,
因此有三种购买方案:
①购买甲型3条,乙型7条;
②购买甲型4条,乙型6条;
③购买甲型5条,乙型5条.
当m=3时,购买资金为:10×3+8×7=86(万元),
当m=4时,购买资金为:10×4+8×6=88(万元),
当m=5时,购买资金为:10×5+8×5=90(万元),
∵86<88<90,
∴最省钱的购买方案为:选购甲型3条,乙型7条,最少费用为86万元.
一、选择题
1、一次生活常识知识竞赛一共有30道题,答对一题得4分,不答得0分,答错扣2分.小聪有2道题没答,竞赛成绩超过80分,则小聪至多答错了________道题.
2、在抗震救灾中,某抢险地段需实行爆破.操作人员点燃导火线后,要在炸药爆炸前跑到以外的安全区域.已知导火线的燃烧速度是,操作人员跑步的速度是6m/s.为了保证操作人员的安全,导火线的长度要超过( )
A. B. C. D.
3、小明要从甲地到乙地,两地相距1.8千米.已知他步行的平均速度为90米/分,跑步的平均速度为210米/分,若他要在不超过15分钟的时间内从甲地到达乙地,至少需要跑步多少分钟?设他需要跑步x分钟,则列出的不等式为( )
A.210x+90(15﹣x)≥1.8 B.90x+210(15﹣x)≤1800
C.210x+90(15﹣x)≥1800 D.90x+210(15﹣x)≤1.8
4、某城市的一种出租车起步价是7元(即在3km以内的都付7元车费),超过3km后,每增加1km加价1.2元(不足1km按1km计算),现某人付了14.2元车费,求这人乘的最大路程是( )
A.10km B.9 km C.8km D.7 km
5、某电信公司推出两种手机收费方案.方案A:月租费30元,本地通话话费0.15元/分;方案B:不收月租费,本地通话话费为0.3元/分.设婷婷的爸爸一个月通话时间为x分钟,婷婷的爸爸一个月通话时间为多少时,选择方案A比方案B优惠?( )
A.100分钟 B.150分钟 C.200分钟 D.250分钟
6、阿慧在店内购买两种蛋糕当伴手礼,如图为蛋糕的价目表.已知阿慧共购买盒蛋糕,花费的金额不超过元.若他将蛋糕分给位同事,每人至少能拿到一个蛋糕,则阿慧花多少元购买蛋糕?( )
A. B. C. D.
7、某种商品的进价为500元,出售时标价为750元,由于换季,商店准备打折销售,但要保持利润不低于20%,那么至多打( )
A.6折 B.7折 C.8折 D.9折
8、小聪去商店购买笔记本和钢笔,共用了60元钱,已知每本笔记本2元,每支钢笔5元,若笔记本和钢笔都需购买,且笔记本的数量多于钢笔的数量,则小聪的购买方案有( )
A.3种 B.4种 C.5种 D.6种
9、小明去商店购买A、B两种玩具,共用了10元钱,A种玩具每件1元,B种玩具每件2元.若每种玩具至少买一件,且A种玩具的数量多于B种玩具的数量.则小明的购买方案有( )
A.5种 B.4种 C.3种 D.2种
10、运行程序如图所示,规定:从“输入一个值x”到“结果是否>26”为一次程序操作,如果程序操作进行
了2次后停止,那么满足条件的所有整数x的和为( )
A.30 B.35 C.42 D.39
二、填空题
11、某商场推出一种购物金卡,凭卡在该商场购物可按商品价格的九折付款,但办理金卡时每张要收50元购卡费,设按标价累计购物金额为x(元),当 时,办理金卡购物省钱.?
12、有10名菜农,每人可种甲种蔬菜3亩或乙种蔬菜2亩,已知甲种蔬菜每亩可收入0.5万元,乙种蔬菜每亩可收入0.8万元,若要使总收入不低于15.6万元,则最多能安排 人种甲种蔬菜.?
13、有学生若干人,住若干间宿舍,若每间住5人,则有14人无法安排住宿,若每间住8人,则最后有一间宿舍不满也不空,则学生人数为_____.
14、某种型号汽车每行驶100km耗油10L,其油箱容量为40L.为了有效延长汽车使用寿命,厂家建议每次加油时邮箱内剩余油量不低于油箱容量的,按此建议,一辆加满油的该型号汽车最多行驶的路程是_____km.
15、甲乙两队进行篮球对抗赛,比赛规则规定每队胜一场得3分,平一场得1分,负一场得0分,两队一共比赛了10场,甲队保持不败,得分不低于24分,甲队至少胜了___________场.
16、某种商品的进价为15元,出售时标价是22.5元.由于市场不景气销售情况不好,商店准备降价处理,但要保证利润率不低于10%,那么该店最多降价______元出售该商品.
17、一次生活常识知识竞赛一共有20道题,答对一题得5分,不答得0分,答错扣2分,小聪有1道题没答,竞赛成绩超过80分,则小聪至少答对了_______道题.
18、疫情过后,地摊经济火爆,张阿姨以每件80元的价格购进50件衬衫,在地摊上以每件100元的价格出售,她至少销售__________件衬衫,所得销售额才能超过进货总价.
19、“一方有难,八方支援”.某学校计划购买84消毒液和75%酒精消毒水共4000瓶,用于支援武汉抗击“新冠肺炎疫情”.已知84消毒液的单价为3元/瓶,75%酒精消毒水的单价为13元/瓶,若购买这批物资的总费用不超过28000元,则至少需要购买84消毒液多少瓶?
20、4月21日是重庆一中校庆日,学校每一年都要举行校庆活动和教职工运动会,全校分校区或年级组队进行角逐,今年某校区给参赛老师购买了、、三种运动服,每一套价格分别是400元,500元,600元,其中种运动服套数是种运动服套数的3倍,种运动服套数比C种运动服套数的2倍还多,要求购买服装的总套数尽量多且总费用不超过52300元,则能购买到运动服最多_________套.
三、解答题
21、一工厂以90元/每箱的价格购进100箱原材料,准备由甲、乙两个车间全部用于生产某种产品,甲车间用每箱原材料可生产出该产品12千克,乙车间用每箱原材料可生产出的该产品比甲车间少2千克,已知该产品的售价为40元/千克,生产的产品全部售出,那么原材料最少分配给甲车间多少箱,才能使去除成本后所获得的总利润不少于35000元?
22、某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方形形状的
无盖纸盒.
(1)现有正方形纸板150张,长方形纸板300张,若这些纸板恰好用完,则可制作横式、竖式两种纸盒各多少个?
(2)若有正方形纸板32张,长方形纸板张,做成上述两种纸盒,纸板恰好用完,已知.
求的值.
23、大浮杨梅是我市特色水果,古称“吴越佳果”.某水果店以20元/千克的价格购进一批杨梅,由于销售状况良好,该店再次购进同一种杨梅,第二次进货价格比第一次每千克便宜了0.5元.该水果店两次共购进杨梅110千克,共花去2160元.
(1)该水果店两次分别购买了多少千克的杨梅?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的杨梅有10%
的损耗,第二次购进的杨梅有15%的损耗,该水果店希望售完这些杨梅获利不低于500元,则该杨梅每千克售价至少为多少元?
24、2020年初,新冠疫情在武汉爆发.“一方有难,八方支援”,某市筹集了大量的生活物资,用,两种型号的货车,分两批运往受灾严重的地区.具体运输情况如下:
第一批 第二批
型货车的辆数(单位:辆) 8 10
型货车的辆数(单位:辆) 4 25
累计运输物资的吨数(单位:吨) 128 400
备注:第一批、第二批每辆货车均满载
(1)求、两种型号货车每辆满载分别能运多少吨生活物资?
(2)该市后续又筹集了262.4吨生活物资,现已联系了6辆种型号货车.试问至少还需联系多少辆 种型号货车才能一次性将这批生活物资运往目的地?
25、某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件.其中甲种奖品每件400元,乙种奖品每件300元.
(1)如果购买甲、乙两种奖品共花费了6500元,求甲、乙两种奖品各购买了多少件;
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过6800元,求该公司有哪几种不同的购买方案.
26、某学校为了增强学生体质,加强体育锻炼,决定让各班购买跳绳和毽子作为活动器材.已知购买2根跳绳和5个毽子共需32元;购买4根跳绳和3个毽子共需36元.
(1)求购买一根跳绳和一个毽子分别需要多少元;
(2)某班需要购买跳绳和毽子的总数量是54,且购买的总费用不能超过260元;若要求购买跳绳的数量多于20根,通过计算说明共有哪几种购买方案.
27、为应对新冠肺炎疫情,某服装厂决定转型生产口罩,根据现有厂房大小决定购买10条口罩生产线,现有甲、乙两种型号的口罩生产线可供选择.经调查:购买3台甲型口罩生产线比购买2台乙型口罩生产线多花14万元,购买4条甲型口罩生产线与购买5条乙型口罩生产线所需款数相同.
(1)求甲、乙两种型号口罩生产线的单价;
(2)已知甲型口罩生产线每天可生产口罩9万只,乙型口罩生产线每天可生产口罩7万只,若每天要求产量不低于75万只,预算购买口罩生产线的资金不超过90万元,该厂有哪几种购买方案?哪种方案最省钱?最少费用是多少?
专题复习提升训练卷11.5用一元一次不等式解决问题-20-21苏科版七年级数学下册(解析)
一、选择题
1、一次生活常识知识竞赛一共有30道题,答对一题得4分,不答得0分,答错扣2分.小聪有2道题没答,竞赛成绩超过80分,则小聪至多答错了________道题.
【答案】5
【分析】设小聪答错了x道题,则答对了(30-x-2)道题,根据总分=5×答对题目数-2×答错题目数结合总分超过80分,即可得出关于x的一元一4,则答对了(30-x-2)道题,
依题意得:,解得:,
∵错题数为整数,∴x最大值为5,故答案为:5.
2、在抗震救灾中,某抢险地段需实行爆破.操作人员点燃导火线后,要在炸药爆炸前跑到以外的安全区域.已知导火线的燃烧速度是,操作人员跑步的速度是6m/s.为了保证操作人员的安全,导火线的长度要超过( )
A. B. C. D.
【答案】A
【分析】根据题意可知:操作人员点燃导火线后,要在炸药爆炸前跑到450米以外的安全区域,列出不等式,解不等式即可.
【详解】解:设导火线长度为xcm,根据题意得, >,
解得x>90,
故选:A.
3、小明要从甲地到乙地,两地相距1.8千米.已知他步行的平均速度为90米/分,跑步的平均速度为210米/分,若他要在不超过15分钟的时间内从甲地到达乙地,至少需要跑步多少分钟?设他需要跑步x分钟,则列出的不等式为( )
A.210x+90(15﹣x)≥1.8 B.90x+210(15﹣x)≤1800
C.210x+90(15﹣x)≥1800 D.90x+210(15﹣x)≤1.8
【答案】C
【分析】根据题意,利用要在不超过15分钟的时间内从甲地到达乙地建立不等式即可解题.
【详解】解:由题可知只需要小明在15分钟之内走过的路程大于1800即可,
即210x+90(15﹣x)≥1800
故选C.
4、某城市的一种出租车起步价是7元(即在3km以内的都付7元车费),超过3km后,每增加1km加价1.2元(不足1km按1km计算),现某人付了14.2元车费,求这人乘的最大路程是( )
A.10km B.9 km C.8km D.7 km
【答案】B
【分析】设路程为x千米,依题意得13<7+1.2(x-3)≤14.2,解不等式即可.注意考虑到不足1千米也按1千米收费.
【详解】解:设路程为x千米,
依题意得13<7+1.2(x-3)≤14.2,
解得8<x≤9,
故这人乘的最大路程是9km,
故选:B
5、某电信公司推出两种手机收费方案.方案A:月租费30元,本地通话话费0.15元/分;方案B:不收月租费,本地通话话费为0.3元/分.设婷婷的爸爸一个月通话时间为x分钟,婷婷的爸爸一个月通话时间为多少时,选择方案A比方案B优惠?( )
A.100分钟 B.150分钟 C.200分钟 D.250分钟
【答案】D
【分析】由题意易得,然后进行求解排除选项即可.
【详解】解:设婷婷的爸爸一个月通话时间为x分钟,由题意得:,
解得:,∴只有D选项符合题意;故选D.
6、阿慧在店内购买两种蛋糕当伴手礼,如图为蛋糕的价目表.已知阿慧共购买盒蛋糕,花费的金额不超过元.若他将蛋糕分给位同事,每人至少能拿到一个蛋糕,则阿慧花多少元购买蛋糕?( )
A. B. C. D.
【答案】D
【分析】可设阿慧购买x盒桂圆蛋糕,则购买(10-x)盒金枣蛋糕,根据不等关系:①购买10盒蛋糕,花费的金额不超过500元;②蛋糕的个数大于等于75个,列出不等式组求解即可.
【详解】解:设阿慧购买x盒桂圆蛋糕,则购买(10-x)盒金枣蛋糕,依题意有
,解得≤x≤,
∵x是整数,∴x=3,
70×3+40×(10-3)=490(元).
答:阿慧花490元购买蛋糕. 故选:D.
7、某种商品的进价为500元,出售时标价为750元,由于换季,商店准备打折销售,但要保持利润不低于20%,那么至多打( )
A.6折 B.7折 C.8折 D.9折
【答案】C
【分析】设该服装打x折销售,根据利润=售价-进价结合利润不低于20%,即可得出关于x的一元一次不
等式,解之取其中的最小值即可得出结论.
【详解】解:设该服装打x折销售,
依题意,得: ,
解得:x≥8.
故选:C.
8、小聪去商店购买笔记本和钢笔,共用了60元钱,已知每本笔记本2元,每支钢笔5元,若笔记本和钢笔都需购买,且笔记本的数量多于钢笔的数量,则小聪的购买方案有( )
A.3种 B.4种 C.5种 D.6种
【答案】B
【分析】设笔记本的数量为x个,钢笔的数量为y个,用笔记本的钱数+钢笔的钱数=60,笔记本数量>钢笔数量,可以列出一元一次不等式,求出其解集,再根据笔记本数,钢笔数必须是整数,确定购买方案.
【详解】(1)设笔记本的数量为x个,钢笔的数量为y个.
由题意得:,
∴,, 解得:.
∵为正整数,∴x为5的倍数,故x的取值为10,15,20,25.
故有四种方案.
故选B.
9、小明去商店购买A、B两种玩具,共用了10元钱,A种玩具每件1元,B种玩具每件2元.若每种玩具至少买一件,且A种玩具的数量多于B种玩具的数量.则小明的购买方案有( )
A.5种 B.4种 C.3种 D.2种
【分析】设小明购买了A种玩具x件,则购买的B种玩具为件,根据题意列出不等式组进行解答便可.
【解析】:设小明购买了A种玩具x件,则购买的B种玩具为件,根据题意得,
,解得,3
∴x=4或6或8,
∴有3种购买方案.
故选:C.
10、运行程序如图所示,规定:从“输入一个值x”到“结果是否>26”为一次程序操作,如果程序操作进行
了2次后停止,那么满足条件的所有整数x的和为( )
A.30 B.35 C.42 D.39
【答案】D
【提示】根据题意可知第一次所得的结果≤26,第二次所得的结果>26,列不等式组并解除不等式组得解后再计算满足条件的所有整数的和即可.
【详解】由题意得,
解不等式①得,x≤9,
解不等式②得,x>,
∴x的取值范围是<x≤9,
∴满足条件的所有整数x的和为4+5+6+7+8+9=39.
故答案选D.
二、填空题
11、某商场推出一种购物金卡,凭卡在该商场购物可按商品价格的九折付款,但办理金卡时每张要收50元购卡费,设按标价累计购物金额为x(元),当 时,办理金卡购物省钱.?
[答案] 500
[解析] 根据题意,得x-0.9x>50,解得x>500,即当购物金额大于500元时,办理金卡购物省钱.
12、有10名菜农,每人可种甲种蔬菜3亩或乙种蔬菜2亩,已知甲种蔬菜每亩可收入0.5万元,乙种蔬菜每亩可收入0.8万元,若要使总收入不低于15.6万元,则最多能安排 人种甲种蔬菜.?
[答案] 4
[解析] 设安排x人种甲种蔬菜,则3x×0.5+2(10-x)×0.8≥15.6,解得x≤4,
所以最多能安排4人种甲种蔬菜.
13、有学生若干人,住若干间宿舍,若每间住5人,则有14人无法安排住宿,若每间住8人,则最后有一间宿舍不满也不空,则学生人数为_____.
【答案】39或44或49
【分析】设共有x间宿舍,则学生数有(5x+14)人,列出不等式组为0<5x+14?8(x?1)<8解出即可.
【详解】设共有x间宿舍,则学生数有(5x+14)人,
根据题意得:0<5x+14?8(x?1)<8,解得<x<,
∵x为整数,∴x=5或6或7,即学生有5x+14=39或5x+14=44或5x+14=49.
即,学生人数是39或44人或49;故答案为:39或44或49.
14、某种型号汽车每行驶100km耗油10L,其油箱容量为40L.为了有效延长汽车使用寿命,厂家建议每次加油时邮箱内剩余油量不低于油箱容量的,按此建议,一辆加满油的该型号汽车最多行驶的路程是_____km.
【答案】350.
【提示】设行驶xkm,由油箱内剩余油量不低于油箱容量的,列出不等式,即可求解.
【详解】设该型号汽车行驶的路程是xkm,
∵油箱内剩余油量不低于油箱容量的,
∴﹣x+40≥40×,解得:x≤350,
答:该辆汽车最多行驶的路程是350km,
故答案为:350.
15、甲乙两队进行篮球对抗赛,比赛规则规定每队胜一场得3分,平一场得1分,负一场得0分,两队一共比赛了10场,甲队保持不败,得分不低于24分,甲队至少胜了___________场.
【答案】7
【分析】设甲队胜了x场,则平了(10-x)场,根据胜一场得3分,平一场得1分,负一场得0分,比赛10场,得分24分,列出不等式,求出x的最小整数解.
【详解】设甲队胜了x场,则平了(10-x)场,
由题意得,3x+(10-x)≥24,解得:x≥7,即甲队至少胜了7场.故答案是:7.
16、某种商品的进价为15元,出售时标价是22.5元.由于市场不景气销售情况不好,商店准备降价处理,但要保证利润率不低于10%,那么该店最多降价______元出售该商品.
【答案】6
【解析】先设最多降价x元出售该商品,则出售的价格是22.5-x-15元,再根据利润率不低于10%,列出不等式即可.
解:设最多降价x元出售该商品,则22.5-x-15≥15×10%,解得x≤6.
故该店最多降价6元出售该商品.
17、一次生活常识知识竞赛一共有20道题,答对一题得5分,不答得0分,答错扣2分,小聪有1道题没答,竞赛成绩超过80分,则小聪至少答对了_______道题.
【答案】17
【分析】设小聪答对了x道题,根据“答对题数×5?答错题数×2>80分”列出不等式,解之可得.
【详解】设小聪答对了x道题,根据题意,得:5x?2(19?x)>80,解得x>16,
∵x为整数,∴x=17,即小聪至少答对了17道题,故答案为:17.
18、疫情过后,地摊经济火爆,张阿姨以每件80元的价格购进50件衬衫,在地摊上以每件100元的价格出售,她至少销售__________件衬衫,所得销售额才能超过进货总价.
【答案】41
【提示】根据题意,可以设销售x件衬衫,然后列出不等式100x>80×50,求出x的取值范围,注意x为整数,从而可以得到x的最小整数值,本题得以解决.
【详解】解:设销售x件衬衫,依题意有100x>80×50,
解得x>40,
∵x为整数,
∴x最小是41.
答:她至少销售41件衬衫,所得销售额才能超过进货总价.
故答案为:41.
19、“一方有难,八方支援”.某学校计划购买84消毒液和75%酒精消毒水共4000瓶,用于支援武汉抗击“新冠肺炎疫情”.已知84消毒液的单价为3元/瓶,75%酒精消毒水的单价为13元/瓶,若购买这批物资的总费用不超过28000元,则至少需要购买84消毒液多少瓶?
解:设需要购买84消毒液x瓶,则购买75%酒精消毒水(4000-x)瓶.依题意,得
3x+13(4000-x)≤28000,
解得x≥2400.
答:至少需要购买84消毒液2400瓶.
20、4月21日是重庆一中校庆日,学校每一年都要举行校庆活动和教职工运动会,全校分校区或年级组队进行角逐,今年某校区给参赛老师购买了、、三种运动服,每一套价格分别是400元,500元,600元,其中种运动服套数是种运动服套数的3倍,种运动服套数比C种运动服套数的2倍还多,要求购买服装的总套数尽量多且总费用不超过52300元,则能购买到运动服最多_________套.
【答案】111
【分析】设C种运动服购买x套,则A种运动服3x套,B种运动服的套数大于2x,由题意列不等式,结合问题的实际意义,且x必须取整可解.
【详解】设C种运动服购买x套,则A种运动服3x套,B种运动服的套数大于2x,由题意得
52300?600x?400×3x>500×2x, ∴52300>2800x
∴x<, ∴2x<
∵x必须为正整数, ∴x的最大值为18
∴应购买A种运动服54套,购买C种运动服18套,
∵(52300?400×54?600×18)÷500=39.8
购买B种运动服39套,
最多能购买54+39+18=111套.
故答案为:111
三、解答题
21、一工厂以90元/每箱的价格购进100箱原材料,准备由甲、乙两个车间全部用于生产某种产品,甲车间用每箱原材料可生产出该产品12千克,乙车间用每箱原材料可生产出的该产品比甲车间少2千克,已知该产品的售价为40元/千克,生产的产品全部售出,那么原材料最少分配给甲车间多少箱,才能使去除成本后所获得的总利润不少于35000元?
【分析】设甲车间用x箱原材料,则乙车间用(100﹣x)箱原材料,根据题意列出不等式,
【解答】解:设甲车间用x箱原材料,则乙车间用(100﹣x)箱原材料,
根据题意,得12x×40+(100﹣x)(12﹣2)×40﹣100×90≥35000.
解得x≥50.
答:原材料最少分配给甲车间50箱,才能使去除成本后所获得的总利润不少于35000元.
22、某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方形形状的
无盖纸盒.
(1)现有正方形纸板150张,长方形纸板300张,若这些纸板恰好用完,则可制作横式、竖式两种纸盒各多少个?
(2)若有正方形纸板32张,长方形纸板张,做成上述两种纸盒,纸板恰好用完,已知.
求的值.
【答案】(1);(2)a=73
【分析】(1)设制作竖式纸盒x个,则制作横式纸盒y个.根据制作竖式纸盒用的正方形纸板+制作横式纸盒用的正方形纸板=150张;制作竖式纸盒用的长方形纸板+制作横式纸盒用的长方形纸板=300张.列方程组即可得到结论;
(2)设x个竖式需要正方形纸板x张,长方形纸板横4x张;y个横式需要正方形纸板2y张,长方形纸板横3y张,可列出方程组,再根据a的取值范围求出y的取值范围即可.
【详解】解:(1)设制作竖式纸盒x个,则制作横式纸盒y个.
由题意得,解得:,
答:可制作横式纸盒60个、竖式纸盒30个;
(2)设制作竖式纸盒x个,则制作横式纸盒y个.由题意得,解得y=,
∵70<a<75,∴53<128-a<58,
∵y是整数,∴128-a=55,∴a=73.
23、大浮杨梅是我市特色水果,古称“吴越佳果”.某水果店以20元/千克的价格购进一批杨梅,由于销售状况良好,该店再次购进同一种杨梅,第二次进货价格比第一次每千克便宜了0.5元.该水果店两次共购进杨梅110千克,共花去2160元.
(1)该水果店两次分别购买了多少千克的杨梅?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的杨梅有10%的损耗,第二次购进的杨梅有15%的损耗,该水果店希望售完这些杨梅获利不低于500元,则该杨梅每千克售价至少为多少元?
【分析】(1)设该水果店两次分别购买了x元和y元的水果.根据“购进同一种水果,第二次进货价格比第一次每千克便宜了0.5元,该水果店两次共购进杨梅110千克,”、“两次购进水果共花去了2160元”列出方程组并解答;
(2)设该水果每千克售价为m元,则由“售完这些水果获利不低于500元”列出不等式并解答.
【解析】(1)设该水果店两次分别购买了x元和y元的水果.根据题意,得
解得:x=30,y=80,
答:水果店两次分别购买了30千克和80千克的杨梅;
(2)设该杨梅每千克售价为m元,根据题意,得:
m[30(1﹣10%)+80(1﹣15%)]﹣2160≥500,
解得:m≥28,
答:该杨梅每千克售价至少为28元.
24、2020年初,新冠疫情在武汉爆发.“一方有难,八方支援”,某市筹集了大量的生活物资,用,两种型号的货车,分两批运往受灾严重的地区.具体运输情况如下:
第一批 第二批
型货车的辆数(单位:辆) 8 10
型货车的辆数(单位:辆) 4 25
累计运输物资的吨数(单位:吨) 128 400
备注:第一批、第二批每辆货车均满载
(1)求、两种型号货车每辆满载分别能运多少吨生活物资?
(2)该市后续又筹集了262.4吨生活物资,现已联系了6辆种型号货车.试问至少还需联系多少辆 种型号货车才能一次性将这批生活物资运往目的地?
【答案】(1)A:10吨,B:12吨;(2)至少需要B型17辆
【分析】
(1)设A,B两种型号货车每辆满载分别能运x,y吨生活物资,根据条件建立方程组求出其解即可;
(2)设还需联系m辆B型号货车才能一次性将这批生活物资运往目的地,根据题中的不等关系列出不等式解答即可.
【详解】(1)设A,B两种型号货车每辆满载分别能运x,y吨生活物资
依题意,得解得
∴A,B两种型号货车每辆满载分别能运10吨,12吨生活物资
(2)设还需联系m辆B型号货车才能一次性将这批生活物资运往目的地
依题意,得.
解得
又m为整数,
∴m最小取17,
∴至少还需联系17辆B型号货车才能一次性将这批生活物资运往目的地.
25、某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件.其中甲种奖品每件400元,乙种奖品每件300元.
(1)如果购买甲、乙两种奖品共花费了6500元,求甲、乙两种奖品各购买了多少件;
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过6800元,求该公司有哪几种不同的购买方案.
【分析】(1)设甲种奖品购买了a件,乙种奖品购买了(20﹣a)件,利用购买甲、乙两种奖品共花费了6500元列方程400a+300(20﹣a)=6500,然后解方程求出a,再计算20﹣a即可;
(2)设甲种奖品购买了x件,乙种奖品购买了(20﹣x)件,利用购买乙种奖品的件数不超过甲种
奖品件数的2倍,总花费不超过680元列不等式组,然后解不等式组后确定x的整数值即可得到该公司的购买方案.
【解析】(1)设甲种奖品购买了a件,乙种奖品购买了(20﹣a)件,
根据题意得400a+300(20﹣a)=6500,解得a=5,
则20﹣a=15,
答:甲种奖品购买了5件,乙种奖品购买了15件;
(2)设甲种奖品购买了x件,乙种奖品购买了(20﹣x)件,
根据题意得,解得x≤8,
∵x为整数,∴x=7或x=8,
当x=7时,20﹣x=13;当x=8时,20﹣x=12;
答:该公司有2种不同的购买方案:
甲种奖品购买了:7件,乙种奖品购买了13件
或甲种奖品购买了8件,乙种奖品购买了12件.
26、某学校为了增强学生体质,加强体育锻炼,决定让各班购买跳绳和毽子作为活动器材.已知购买2根跳绳和5个毽子共需32元;购买4根跳绳和3个毽子共需36元.
(1)求购买一根跳绳和一个毽子分别需要多少元;
(2)某班需要购买跳绳和毽子的总数量是54,且购买的总费用不能超过260元;若要求购买跳绳的数量多于20根,通过计算说明共有哪几种购买方案.
【答案】(1)购买一根跳绳需要6元,购买一个毽子需要4元;
(2)共有2种购买方案,方案1:购买21根跳绳,33个毽子;方案2:购买22根跳绳,32个毽子.
【分析】(1)设购买一根跳绳需要x元,购买一个毽子需要y元,根据“购买2根跳绳和5个毽子共需32元;购买4根跳绳和3个毽子共需36元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购买m根跳绳,则购买(54?m)个毽子,根据购买的总费用不能超过260元且购买跳绳的数量多于20根,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,结合m为正整数即可得出各购买方案.
【详解】解:(1)设购买一根跳绳需要x元,购买一个毽子需要y元,
依题意,得:,解得:.
答:购买一根跳绳需要6元,购买一个毽子需要4元;
(2)设购买m根跳绳,则购买(54?m)个毽子,
依题意,得:,解得:20<m≤22.
又∵m为正整数,∴m可以为21,22.
∴共有2种购买方案,
方案1:购买21根跳绳,33个毽子;
方案2:购买22根跳绳,32个毽子.
27、为应对新冠肺炎疫情,某服装厂决定转型生产口罩,根据现有厂房大小决定购买10条口罩生产线,现有甲、乙两种型号的口罩生产线可供选择.经调查:购买3台甲型口罩生产线比购买2台乙型口罩生产线多花14万元,购买4条甲型口罩生产线与购买5条乙型口罩生产线所需款数相同.
(1)求甲、乙两种型号口罩生产线的单价;
(2)已知甲型口罩生产线每天可生产口罩9万只,乙型口罩生产线每天可生产口罩7万只,若每天要求产量不低于75万只,预算购买口罩生产线的资金不超过90万元,该厂有哪几种购买方案?哪种方案最省钱?最少费用是多少?
【分析】(1)设未知数,列二元一次方程组可以求解,
(2)设购买甲设备a台,根据购买甲型设备不少于3台,和购买甲、乙两种新设备的资金不超过110万元,列出不等式组,根据不等式组的整数解得出购买方案.
【解析】(1)设甲型号口罩生产线的单价为x万元,乙型号口罩生产线的单价为y万元,由题意得:
, 解得:,
答:甲型号口罩生产线的单价为10万元,乙型号口罩生产线的单价为8万元.
(2)设购买甲型号口罩生产线m条,则购买乙型号口罩生产线(10﹣m)条,由题意得:
, 解得:2.5≤m≤5,
又∵m为整数,∴m=3,或m=4,或m=5,
因此有三种购买方案:
①购买甲型3条,乙型7条;
②购买甲型4条,乙型6条;
③购买甲型5条,乙型5条.
当m=3时,购买资金为:10×3+8×7=86(万元),
当m=4时,购买资金为:10×4+8×6=88(万元),
当m=5时,购买资金为:10×5+8×5=90(万元),
∵86<88<90,
∴最省钱的购买方案为:选购甲型3条,乙型7条,最少费用为86万元.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
