2020-2021学年北师大版八年级数学下册6.1第1课时平行四边形边和角的性质课件(共20张PPT)
文档属性
| 名称 | 2020-2021学年北师大版八年级数学下册6.1第1课时平行四边形边和角的性质课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 338.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-06 23:45:20 | ||
图片预览







文档简介
6.1 平行四边形的性质
第六章 平行四边形
第1课时 平行四边形边和角的性质
复习回顾
这里面包含了我们小学时所学过的什么图形?
平行四边形的定义: _______________ 的四边形叫做平行四边形.
平行四边形_____________连成的线段叫做对角线
预习检测
平行四边形的性质:平行四边形的对边_________
平行四边形的对角_________
将一张纸对折,剪下两张叠放的三角形纸片.
(1)你剪出的这两个三角形有什么样的关系?
把四边形中不相邻即相对的边叫对边,相对的角叫对角.
(2)将重叠的两个三角形绕相等边中点旋转180°,你拼得一个怎样的图形?共有几种?与同伴交流.
新课引入
(3)如图1,这个四边形的两组对边有怎样的位置 关系?说说你的理由.
∵△ABD≌△CDB
∴∠1=∠2, ∠3=∠4
(全等三角形对应角相等)
∴ AD∥BC , AB∥CD
(内错角相等,两直线平行)
图1
∴这个四边形的两组对边分别平行.
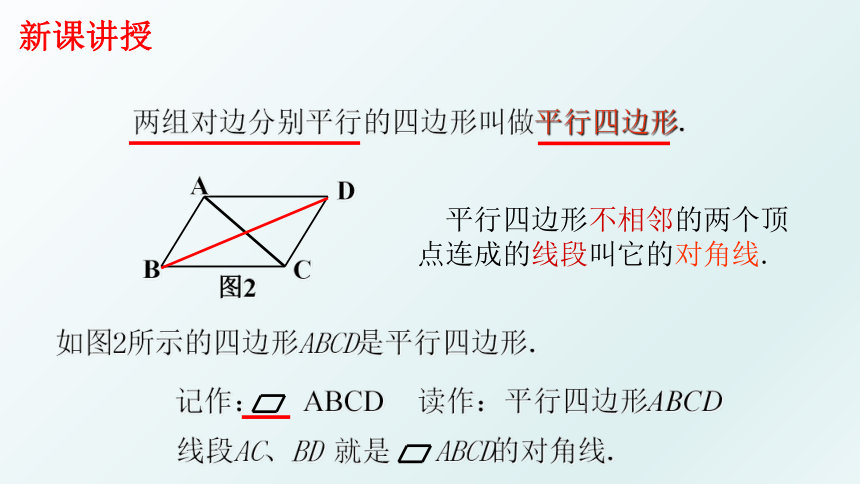
两组对边分别平行的四边形叫做平行四边形.
平行四边形不相邻的两个顶
点连成的线段叫它的对角线.
如图2所示的四边形ABCD是平行四边形.
线段AC、BD 就是 ABCD的对角线.
记作: ABCD
读作:平行四边形ABCD
图2
A
D
B
C
新课讲授
平行四边形
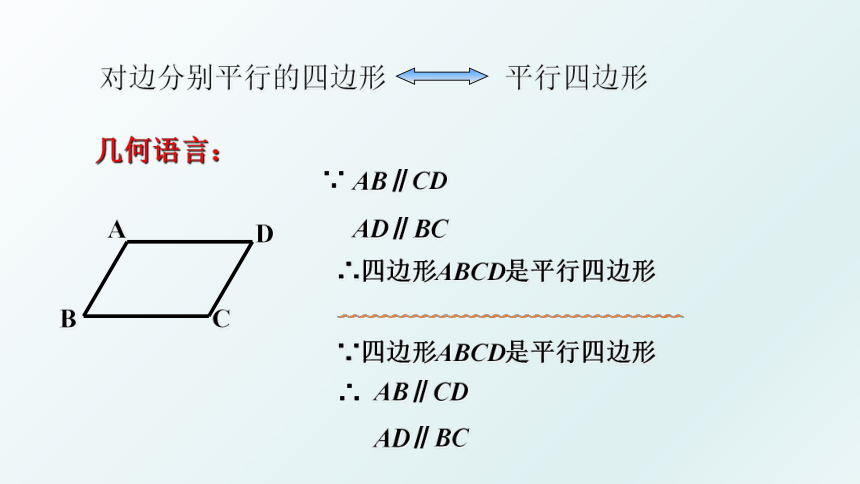
对边分别平行的四边形
几何语言:
∵四边形ABCD是平行四边形
∴四边形ABCD是平行四边形
AD∥BC
AB∥CD
∴
AD∥BC
AB∥CD
∵
A
D
B
C
操作活动:用一张半透明的纸复制你刚才画的平行四边形,并将复制后的四边形绕一个顶点旋转180度,你能平移该纸片,使它与你画的平行四边形ABCD重合吗?
结论2:平行四边形的对边相等
平行四边形的对角相等
讨论:
(1)通过以上活动,你能得到哪些结论?
(2)四边形ABCD对边、对角分别有什么关系?能用别的方法验证你的结论吗?
结论1:平行四边形是中心对称图形,
两条对角线的交点是他的对称中心
例:如图6-2(1),四边形ABCD是平行四边形.
求证:AB=CD,BC=DA.
1
2
3
4
证明:如图6-2(2),连接AC.
∵ 四边形ABCD是平行四边形
∴ AD // BC,AB // CD
∴ ∠1=∠2,∠3=∠4
∴ △ABC和△CDA中
∠2=∠1
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴ AB=DC, AD=CB
1
2
3
4
例:如图6-2(1),四边形ABCD是平行四边形.
求证: ∠A=∠C,∠B=∠D.
1
2
3
4
证明:如图,连接AC.
∵ 四边形ABCD是平行四边形
∴ AD // BC, AB // CD
∴ ∠A+∠B=180 °
∠A+∠D=180 °
∴ ∠B=∠D
同理可得:∠A=∠C
1.填空:
(1)平行四边形___平行,___相等,___相等;
(2)如下图 中,EF∥BC, GH∥AB, EF与GH相交于点O,则图中共有___个平行四边形.
ABCD
对边
对边
对角
9
A
O
H
F
E
D
C
B
G
随堂训练
2.如图,四边形ABCD是平行四边形,求:
(1)∠ADC,∠BCD的度数;
(2)边AB,BC的长度.
解:(1)∵四边形ABCD是平行四边形
A
D
B
C
30
25
56°
∴∠B=∠ADC(平行四边形对角相等)
AB∥CD(平行四边形对边平行)
∴∠B+∠BCD=180°
(两直线平行,同旁内角互补)
∵∠B=56°
∴∠ADC=∠B=56°
∠BCD=180°-∠B=180°-56°=124°
3.四边形ABCD是平行四边形,它的四条边中哪些线段可以通过平移而相互得到?
4. 中,E、F过AC中点O,交AD、BC于E、F,请说明:OE=OF.
ABCD
A
B
C
D
E
F
O
(2)∵四边形ABCD是平行四边形
∴AD=BC,AB=CD(平行四边形对边相等)
∵AD=30,CD=25 ∴BC=30,AB=25.
1、本节课研究了什么图形的性质?
2、什么是平行四边形?
3、从本节课的探讨中,平行四边形有哪些性质?
4、平行四边形还有哪些性质?
课堂小结
第六章 平行四边形
第1课时 平行四边形边和角的性质
复习回顾
这里面包含了我们小学时所学过的什么图形?
平行四边形的定义: _______________ 的四边形叫做平行四边形.
平行四边形_____________连成的线段叫做对角线
预习检测
平行四边形的性质:平行四边形的对边_________
平行四边形的对角_________
将一张纸对折,剪下两张叠放的三角形纸片.
(1)你剪出的这两个三角形有什么样的关系?
把四边形中不相邻即相对的边叫对边,相对的角叫对角.
(2)将重叠的两个三角形绕相等边中点旋转180°,你拼得一个怎样的图形?共有几种?与同伴交流.
新课引入
(3)如图1,这个四边形的两组对边有怎样的位置 关系?说说你的理由.
∵△ABD≌△CDB
∴∠1=∠2, ∠3=∠4
(全等三角形对应角相等)
∴ AD∥BC , AB∥CD
(内错角相等,两直线平行)
图1
∴这个四边形的两组对边分别平行.
两组对边分别平行的四边形叫做平行四边形.
平行四边形不相邻的两个顶
点连成的线段叫它的对角线.
如图2所示的四边形ABCD是平行四边形.
线段AC、BD 就是 ABCD的对角线.
记作: ABCD
读作:平行四边形ABCD
图2
A
D
B
C
新课讲授
平行四边形
对边分别平行的四边形
几何语言:
∵四边形ABCD是平行四边形
∴四边形ABCD是平行四边形
AD∥BC
AB∥CD
∴
AD∥BC
AB∥CD
∵
A
D
B
C
操作活动:用一张半透明的纸复制你刚才画的平行四边形,并将复制后的四边形绕一个顶点旋转180度,你能平移该纸片,使它与你画的平行四边形ABCD重合吗?
结论2:平行四边形的对边相等
平行四边形的对角相等
讨论:
(1)通过以上活动,你能得到哪些结论?
(2)四边形ABCD对边、对角分别有什么关系?能用别的方法验证你的结论吗?
结论1:平行四边形是中心对称图形,
两条对角线的交点是他的对称中心
例:如图6-2(1),四边形ABCD是平行四边形.
求证:AB=CD,BC=DA.
1
2
3
4
证明:如图6-2(2),连接AC.
∵ 四边形ABCD是平行四边形
∴ AD // BC,AB // CD
∴ ∠1=∠2,∠3=∠4
∴ △ABC和△CDA中
∠2=∠1
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴ AB=DC, AD=CB
1
2
3
4
例:如图6-2(1),四边形ABCD是平行四边形.
求证: ∠A=∠C,∠B=∠D.
1
2
3
4
证明:如图,连接AC.
∵ 四边形ABCD是平行四边形
∴ AD // BC, AB // CD
∴ ∠A+∠B=180 °
∠A+∠D=180 °
∴ ∠B=∠D
同理可得:∠A=∠C
1.填空:
(1)平行四边形___平行,___相等,___相等;
(2)如下图 中,EF∥BC, GH∥AB, EF与GH相交于点O,则图中共有___个平行四边形.
ABCD
对边
对边
对角
9
A
O
H
F
E
D
C
B
G
随堂训练
2.如图,四边形ABCD是平行四边形,求:
(1)∠ADC,∠BCD的度数;
(2)边AB,BC的长度.
解:(1)∵四边形ABCD是平行四边形
A
D
B
C
30
25
56°
∴∠B=∠ADC(平行四边形对角相等)
AB∥CD(平行四边形对边平行)
∴∠B+∠BCD=180°
(两直线平行,同旁内角互补)
∵∠B=56°
∴∠ADC=∠B=56°
∠BCD=180°-∠B=180°-56°=124°
3.四边形ABCD是平行四边形,它的四条边中哪些线段可以通过平移而相互得到?
4. 中,E、F过AC中点O,交AD、BC于E、F,请说明:OE=OF.
ABCD
A
B
C
D
E
F
O
(2)∵四边形ABCD是平行四边形
∴AD=BC,AB=CD(平行四边形对边相等)
∵AD=30,CD=25 ∴BC=30,AB=25.
1、本节课研究了什么图形的性质?
2、什么是平行四边形?
3、从本节课的探讨中,平行四边形有哪些性质?
4、平行四边形还有哪些性质?
课堂小结
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
