七年级数学三角形内角和定理的说课
文档属性
| 名称 | 七年级数学三角形内角和定理的说课 |  | |
| 格式 | zip | ||
| 文件大小 | 554.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-03 20:55:07 | ||
图片预览





文档简介
(共23张PPT)
认真 勤奋 拼搏 进取
认真 勤奋 拼搏 进取
⒎2 与三角形有关的角
三角形的内角
1、课 题: 人教版七年级下第七章第二节《 与三角形有关的角—三角形的内角》
2、 教材简析: 三角形的内角和定理是从“数量关系”揭示三角形内角之间的关系的,这个定理是任意三角形的一个重要性质,它是学习以后知识的基础,并且是计算角的度数的方法之一。在解决四边形内角和多边形的内角和时都将转化为三角形的内角和来解决。其中辅助线的作法、把新知识转化为旧知识、用代数方法解决几何问题,为以后的学习打下良好的基础,三角形内角和定理在理论和实践中有广泛的应用。
三角形内角和定理的内容,学生在小学已经熟悉,
但在小学是通过实验得到的,而观察,实验得出的结论 不一定正确,可靠,那么要想当作定理来用,必须经过推理论证,前面学生已经学习了三角形 的有关概念,平角的 定义和平行线的性质,而定理的证明是借助辅助线 ,
㈠ 教材说明
平行线间的同旁内角,为定理的证明提供了必备的条件,尽管前面学生接触过推理论证,但并未真正论证过,特别是在格式上没有很好的锻炼,因此定理的证明应是本节引导和探索的重点,而辅助线的添加也是解决数学问题(尤其是几何问题) 的重要思想方法,学生也是第一次接触,只要教师设置恰当的问题情境,再由学生实验操作,观察,抽象出几何图形用自主探索的方式是可以完成的,这样的过程可以更好的发展学生的创造能力和实验能力. 从本节开始训练学生将命题翻译为几何符号语言,写出已知,求证,学生分析命题的证明思路,对培养学生的思维能力和推理能力将起到重要的作用,
将三角形的三内角巧妙的转化为一个平角,或两平行线间的同旁内角,为定理的证明提供了必备的条件,尽管前面学生接触过推理论证,但并未真正论证过,特别是在格式上没有很好的锻炼,因此定理的证明应是本节引导和探索的重点,而辅助线的添加也是解决数学问题(尤其是几何问题) 的重要思想方法,学生也是第一次接触,只要教师设置恰当的问题情境,再由学生实验操作,观察,抽象出几何图形用自主探索的方式是可以完成的,这样的过程可以更好的发展学生的创造能力和实验能力.
从本节开始训练学生将命题翻译为几何符号语言,写出已知,求证,学生分析命题的证明思路,对培养学生的思维能力和推理能力将起到重要的作用,
3 教学目标
﹙1﹚ 教学知识目标 : 三角形内角和定理的证明
﹙2﹚ 能力训练目标 :掌握三角形内角和定理 ,并初步学会利用辅助线证明,同时培养学生观察、猜想、和论证能力。
﹙3﹚ 情感与价值目标 :通过新颖、有趣的实际问题,来激发学生的求知欲。
4 教学重点
三角形内角和定理的证明思路及应用。
5 教学难点
三角形内角和定理的证明方法及辅助线的产生和作法
㈡ 教法和学法说明
根据本节教学内容的特点,选用了实验,讨论自主探究的教学方法.让学生实际动手撕一下拼一拼自主探究的方法得到新知识,把教学过程转化为亲自实验,讨论探索的过程,再现了知识的“发现”及“形成”的过程,符合学生的认知规律.既提高了学生的学习兴趣.增强信心,也有益于形成数学能力,体现了“数学教学主要是数学活动的教学”这一教育思想.
引导学生在获取知识的过程中,学会观察,概括.表达.论证的方法,发展学生数学思维的深刻性,灵活性与创造性
. ㈢ 德育渗透
激励学生的求知欲望,培养学生动手动脑勇于探索刻苦钻研的精神
内角三兄弟之争
在一个直角三角形里住着三个内角,平时,他们三兄弟非常团结.可是有一天,老二 突然不高兴,发起脾气来,它指着老大说:”你凭什么度数最大呢 ,我也要和你一样大.”不行啊!”老大说:”这是不可能的,否则咱这个家就再也围不起来了”…..为什么,老二很纳闷.
同学们你知道其中的道理吗
㈣教学程序
1、引人新课,激发兴趣。
本节课,我是这样引入的,请听故事:
同学们思考片刻说出了其中的道理,那么三角形的内角和为什么是180°呢 此时引出课题只要同学们学了本节的知识后,就会明
白其中的道理,并帮老二解开心中的疙瘩.
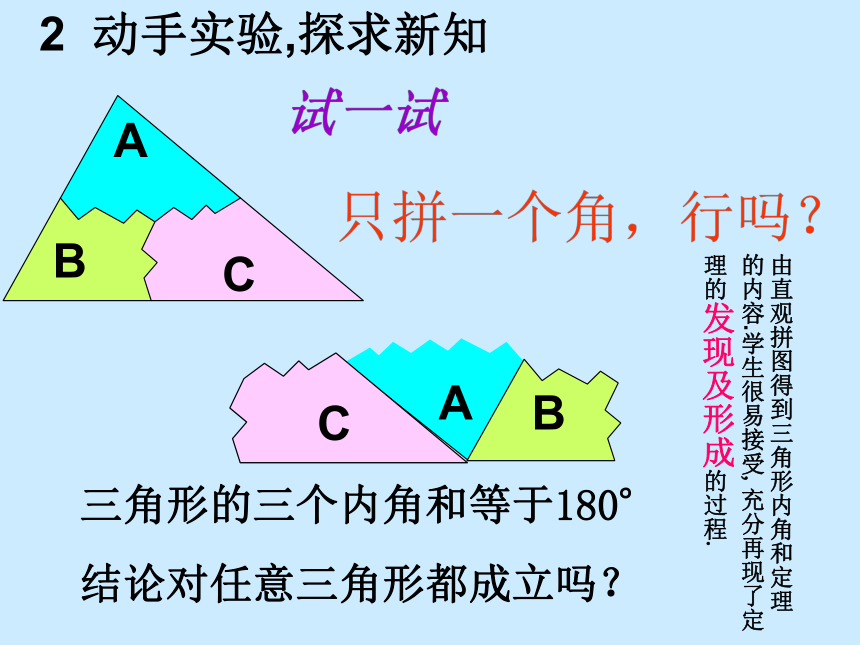
2 动手实验,探求新知
A
B
C
C
A
B
三角形的三个内角和等于
180
°
结论对任意三角形都成立吗?
由直观拼图得到三角形内角和定理 的内容.学生很易接受,充分再现了定理的发现及形成的过程.
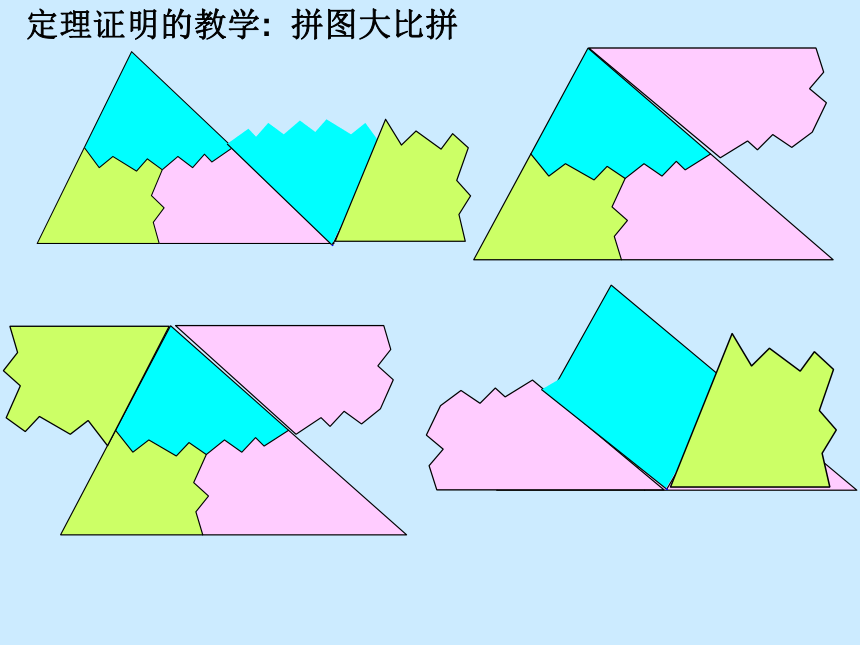
定理证明的教学: 拼图大比拼
图1
E
A
B
C
D
F
图
4
E
A
B
C
D
F
图
图2
A
N
B
C
T
S
图
5
P
Q
R
M
A
N
B
C
T
S
图
5
P
Q
R
M
N
B
C
T
S
图
5
P
Q
R
M
已知:△ABC,
求证:∠A+∠B+∠C=180°
数学推理
这个环节这样设计,主要是让学 生 动起来,主动参与到教学中来.学生动手拼图,主动思考,积极探索,学会转化.从而找到了不同添加辅助线的方法,使重点得以实现,难点得到突破.既培养了学生的发散思维,又锻炼了学生思维的灵活性和广阔性,从而体现了“数学教学主要是数学活动的教学”这一教学思想
到此,你能解释开头提出的问题吗
例1:如图所示,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B
岛的北偏西40°方向,从C岛看A,B两岛的视
角∠ACB是多少度?
北
北
三角形内角和定理的应用:
你还有别的解法吗
例2:已知:在△ABC中,∠C=∠ABC=2∠A ,
BD 是AC 边上的高,请你补上此题的结
论并解答
感觉如何,你成功了吗
教学反思与小结:
这节课,在探究添加辅助线的过程中,可能有同学的拼图不能指导学生合理的添加辅助线,是不成功的拼图.教师要及时的加以点拨,从而培养学生实事求是的精神.
本节课的小结我准备强调以小几点:
(1)肯定学生积极的实验,自主探索的精神,以后的学习中要继续发扬.
(2) 我们证明了一个很有用的三角形的内角和定理,证明思想是运用辅助线将原三角形中处于不同位置的三个内角拼成一个平角,或两平行线间的同旁内角.辅助线是联系命题的条件和结论的桥梁,今后我们还要学习它.
(3)在运用三角形内角和定理时,关键是如何把与条件结论有关的角放在同一个三角形中.使问题得到解决.
作业:
课本76页
1,3,4.
认真 勤奋 拼搏 进取
认真 勤奋 拼搏 进取
See you later!
认真 勤奋 拼搏 进取
认真 勤奋 拼搏 进取
⒎2 与三角形有关的角
三角形的内角
1、课 题: 人教版七年级下第七章第二节《 与三角形有关的角—三角形的内角》
2、 教材简析: 三角形的内角和定理是从“数量关系”揭示三角形内角之间的关系的,这个定理是任意三角形的一个重要性质,它是学习以后知识的基础,并且是计算角的度数的方法之一。在解决四边形内角和多边形的内角和时都将转化为三角形的内角和来解决。其中辅助线的作法、把新知识转化为旧知识、用代数方法解决几何问题,为以后的学习打下良好的基础,三角形内角和定理在理论和实践中有广泛的应用。
三角形内角和定理的内容,学生在小学已经熟悉,
但在小学是通过实验得到的,而观察,实验得出的结论 不一定正确,可靠,那么要想当作定理来用,必须经过推理论证,前面学生已经学习了三角形 的有关概念,平角的 定义和平行线的性质,而定理的证明是借助辅助线 ,
㈠ 教材说明
平行线间的同旁内角,为定理的证明提供了必备的条件,尽管前面学生接触过推理论证,但并未真正论证过,特别是在格式上没有很好的锻炼,因此定理的证明应是本节引导和探索的重点,而辅助线的添加也是解决数学问题(尤其是几何问题) 的重要思想方法,学生也是第一次接触,只要教师设置恰当的问题情境,再由学生实验操作,观察,抽象出几何图形用自主探索的方式是可以完成的,这样的过程可以更好的发展学生的创造能力和实验能力. 从本节开始训练学生将命题翻译为几何符号语言,写出已知,求证,学生分析命题的证明思路,对培养学生的思维能力和推理能力将起到重要的作用,
将三角形的三内角巧妙的转化为一个平角,或两平行线间的同旁内角,为定理的证明提供了必备的条件,尽管前面学生接触过推理论证,但并未真正论证过,特别是在格式上没有很好的锻炼,因此定理的证明应是本节引导和探索的重点,而辅助线的添加也是解决数学问题(尤其是几何问题) 的重要思想方法,学生也是第一次接触,只要教师设置恰当的问题情境,再由学生实验操作,观察,抽象出几何图形用自主探索的方式是可以完成的,这样的过程可以更好的发展学生的创造能力和实验能力.
从本节开始训练学生将命题翻译为几何符号语言,写出已知,求证,学生分析命题的证明思路,对培养学生的思维能力和推理能力将起到重要的作用,
3 教学目标
﹙1﹚ 教学知识目标 : 三角形内角和定理的证明
﹙2﹚ 能力训练目标 :掌握三角形内角和定理 ,并初步学会利用辅助线证明,同时培养学生观察、猜想、和论证能力。
﹙3﹚ 情感与价值目标 :通过新颖、有趣的实际问题,来激发学生的求知欲。
4 教学重点
三角形内角和定理的证明思路及应用。
5 教学难点
三角形内角和定理的证明方法及辅助线的产生和作法
㈡ 教法和学法说明
根据本节教学内容的特点,选用了实验,讨论自主探究的教学方法.让学生实际动手撕一下拼一拼自主探究的方法得到新知识,把教学过程转化为亲自实验,讨论探索的过程,再现了知识的“发现”及“形成”的过程,符合学生的认知规律.既提高了学生的学习兴趣.增强信心,也有益于形成数学能力,体现了“数学教学主要是数学活动的教学”这一教育思想.
引导学生在获取知识的过程中,学会观察,概括.表达.论证的方法,发展学生数学思维的深刻性,灵活性与创造性
. ㈢ 德育渗透
激励学生的求知欲望,培养学生动手动脑勇于探索刻苦钻研的精神
内角三兄弟之争
在一个直角三角形里住着三个内角,平时,他们三兄弟非常团结.可是有一天,老二 突然不高兴,发起脾气来,它指着老大说:”你凭什么度数最大呢 ,我也要和你一样大.”不行啊!”老大说:”这是不可能的,否则咱这个家就再也围不起来了”…..为什么,老二很纳闷.
同学们你知道其中的道理吗
㈣教学程序
1、引人新课,激发兴趣。
本节课,我是这样引入的,请听故事:
同学们思考片刻说出了其中的道理,那么三角形的内角和为什么是180°呢 此时引出课题只要同学们学了本节的知识后,就会明
白其中的道理,并帮老二解开心中的疙瘩.
2 动手实验,探求新知
A
B
C
C
A
B
三角形的三个内角和等于
180
°
结论对任意三角形都成立吗?
由直观拼图得到三角形内角和定理 的内容.学生很易接受,充分再现了定理的发现及形成的过程.
定理证明的教学: 拼图大比拼
图1
E
A
B
C
D
F
图
4
E
A
B
C
D
F
图
图2
A
N
B
C
T
S
图
5
P
Q
R
M
A
N
B
C
T
S
图
5
P
Q
R
M
N
B
C
T
S
图
5
P
Q
R
M
已知:△ABC,
求证:∠A+∠B+∠C=180°
数学推理
这个环节这样设计,主要是让学 生 动起来,主动参与到教学中来.学生动手拼图,主动思考,积极探索,学会转化.从而找到了不同添加辅助线的方法,使重点得以实现,难点得到突破.既培养了学生的发散思维,又锻炼了学生思维的灵活性和广阔性,从而体现了“数学教学主要是数学活动的教学”这一教学思想
到此,你能解释开头提出的问题吗
例1:如图所示,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B
岛的北偏西40°方向,从C岛看A,B两岛的视
角∠ACB是多少度?
北
北
三角形内角和定理的应用:
你还有别的解法吗
例2:已知:在△ABC中,∠C=∠ABC=2∠A ,
BD 是AC 边上的高,请你补上此题的结
论并解答
感觉如何,你成功了吗
教学反思与小结:
这节课,在探究添加辅助线的过程中,可能有同学的拼图不能指导学生合理的添加辅助线,是不成功的拼图.教师要及时的加以点拨,从而培养学生实事求是的精神.
本节课的小结我准备强调以小几点:
(1)肯定学生积极的实验,自主探索的精神,以后的学习中要继续发扬.
(2) 我们证明了一个很有用的三角形的内角和定理,证明思想是运用辅助线将原三角形中处于不同位置的三个内角拼成一个平角,或两平行线间的同旁内角.辅助线是联系命题的条件和结论的桥梁,今后我们还要学习它.
(3)在运用三角形内角和定理时,关键是如何把与条件结论有关的角放在同一个三角形中.使问题得到解决.
作业:
课本76页
1,3,4.
认真 勤奋 拼搏 进取
认真 勤奋 拼搏 进取
See you later!
