人教版19.1.1平行四边形的性质
文档属性
| 名称 | 人教版19.1.1平行四边形的性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-11 00:00:00 | ||
图片预览


文档简介
(共23张PPT)
19.1 平行四边形的性质
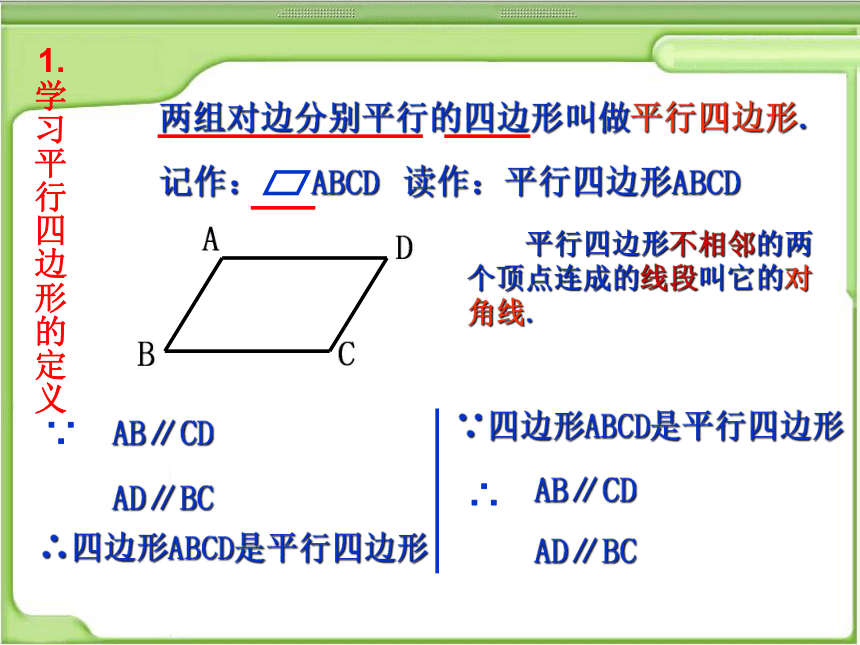
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
平行四边形不相邻的两个顶点连成的线段叫它的对角线.
学习平行四边形的定义
1.
2.探讨平行四边形的性质
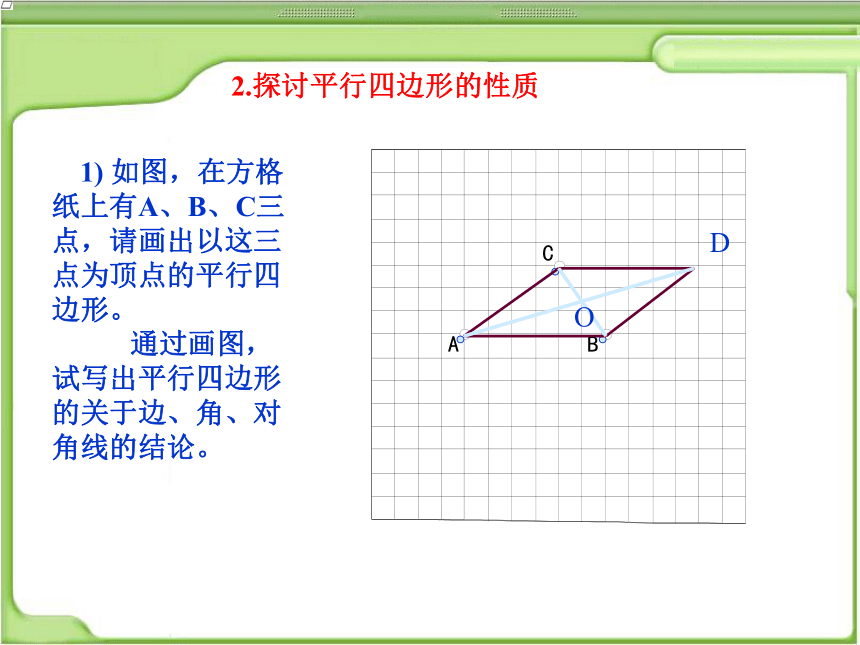
1) 如图,在方格纸上有A、B、C三点,请画出以这三点为顶点的平行四边形。
通过画图,试写出平行四边形的关于边、角、对角线的结论。
D
O
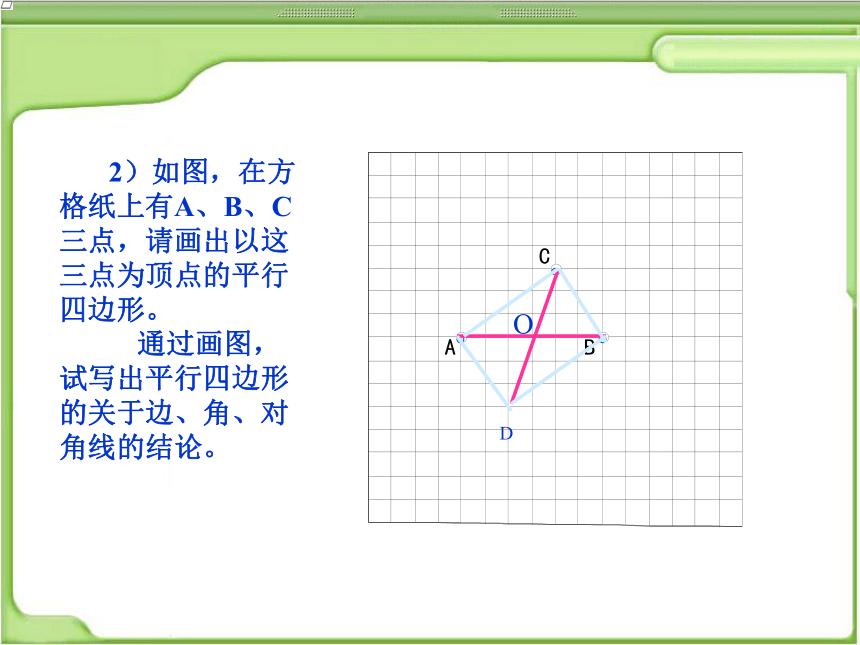
2)如图,在方格纸上有A、B、C三点,请画出以这三点为顶点的平行四边形。
通过画图,试写出平行四边形的关于边、角、对角线的结论。
O
D
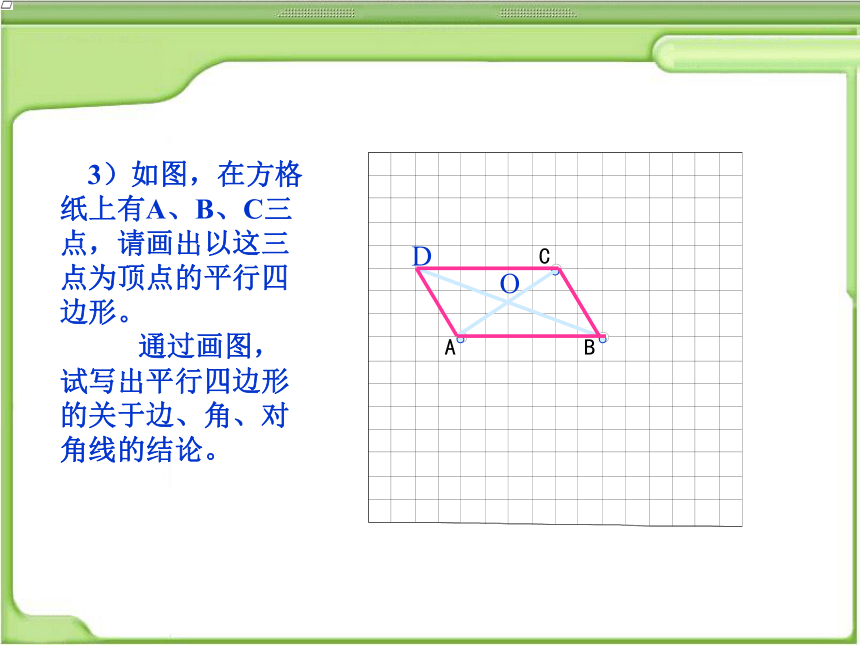
3)如图,在方格纸上有A、B、C三点,请画出以这三点为顶点的平行四边形。
通过画图,试写出平行四边形的关于边、角、对角线的结论。
O
D
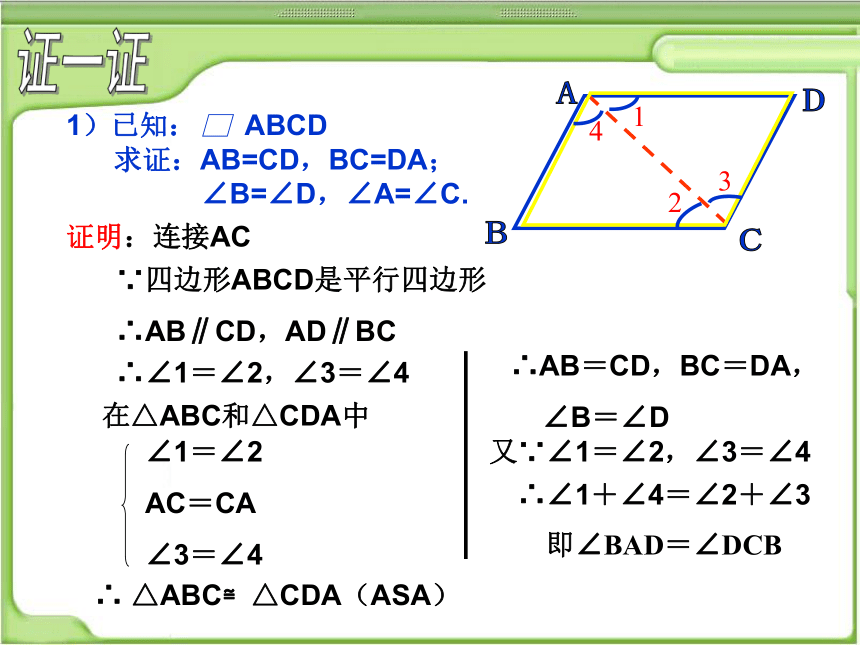
1)已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
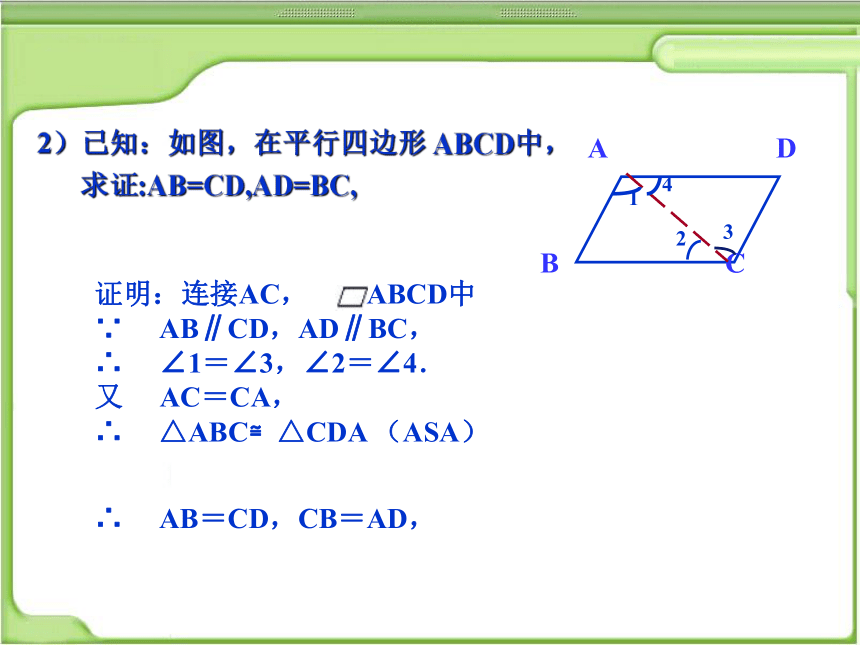
2)已知:如图,在平行四边形 ABCD中,
求证:AB=CD,AD=BC,
证明:连接AC, ABCD中
∵ AB∥CD,AD∥BC,
∴ ∠1=∠3,∠2=∠4.
又 AC=CA,
∴ △ABC≌△CDA (ASA)
∴ AB=CD,CB=AD,
A
D
C
B
1
4
2
3
3)已知:如图,在平行四边形 ABCD中,
求证:∠A=∠C, ∠B=∠D
证明:连接AC, ABCD中
∵ AB∥CD,AD∥BC,
∴ ∠1=∠3,∠2=∠4.
又 AC=CA,
∴ △ABC≌△CDA (ASA)
∴ ∠B=∠D.
又∵ ∠1+∠4=∠2+∠3,
∴ ∠BAD=∠BCD.
A
D
C
B
1
4
2
3
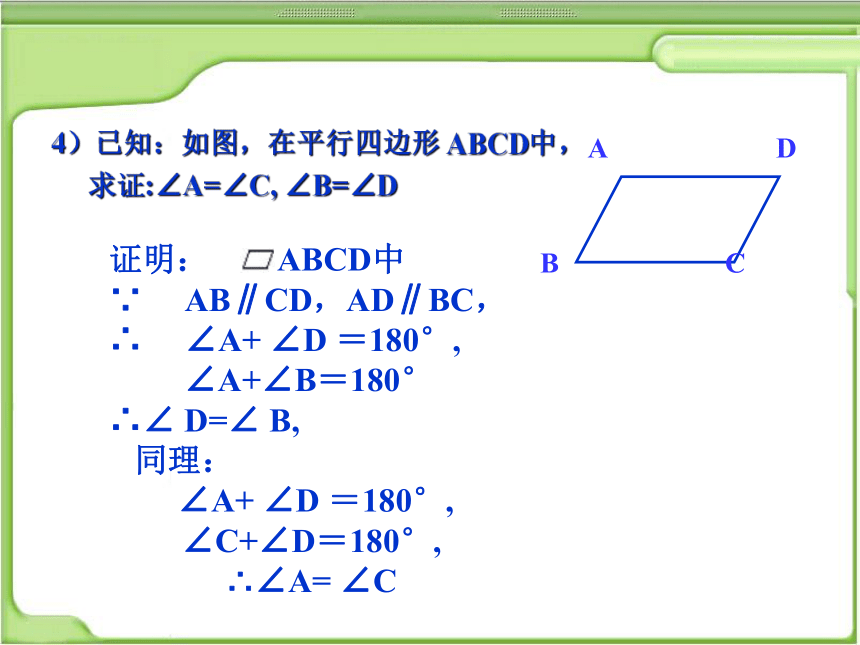
4)已知:如图,在平行四边形 ABCD中,
求证:∠A=∠C, ∠B=∠D
证明: ABCD中
∵ AB∥CD,AD∥BC,
∴ ∠A+ ∠D =180°,
∠A+∠B=180°
∴∠ D=∠ B,
同理:
∠A+ ∠D =180°,
∠C+∠D=180°,
∴∠A= ∠C
A
D
C
B
5)如图:在 ABCD中,AC与BD相交
与点O。
求证:OA=OC OB=OD
1
4
2
3
A
D
C
B
o
证明: ABCD中
∵ AD∥BC,
∴ ∠1=∠3,∠2=∠4.
又 AD=BC,
∴ △BOC≌△DOA(ASA)
∴ OA=OC OB=OD
研究对象 研究结果 几何表示法
边 对边
邻边
角 对角
邻角
对角线
3. 归纳平行四边形的性质
A
D
C
B
平行且相等
相等
互补
∠A=∠C,∠B=∠D
AB∥CD,AD∥BC
=
=
∠A+∠B=180°(略)
互相平分
AO=CO , BO=DO
O
B
A
C
D
邻边之和相等
AB+BC=AD+DC
例 1、如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m.
⑵ 若∠A+∠C=200°,
则∠A和∠B分别为多少度?
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC.
∵AB=8,
∴CD=8(m),
又AB+BC+CD+AD=36, ∴AD=BC=10(m).
解:∵四边形ABCD是平行四边形,
∴∠A=∠C, ∠A+∠B=180°.
∵∠A+∠C=200°,
∴∠A=100°,∠B=80°.
⑴ 其他三条边各长多少?
4.例题赏析
例2,如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长以及 ABCD的面积.
8
10
B
C
D
A
●
O
解:
∴△ABC是直角三角形
又∵AC⊥BC
∵四边形ABCD是平行四边形
∴BC=AD=8,CD=AB=10
又∵OA=OC
∴
∴
∴S = BC×AC=8×6=48
ABCD
1)在 ABCD中, AB=3cm,BC=8cm,则 ABCD的周长
是 cm.
2) ABCD的周长为30cm,两邻边之比为2﹕1,则 ABCD
的两邻边长分别为 .
3) ABCD的周长为30cm,AB比BC长5cm,则AB= cm,
CD= cm.
4)如图,在 ABCD中,∠B的平分线BE
交AD于E,BC=5,AB=3,则ED的长为 .
5)在 ABCD中,已知∠A=130°,则∠B=__ ,
∠C=___ ,∠D=__.
(第4题)
22
10cm,5cm
2
10
10
5. 练习反馈
50°
130°
50°
6) 中,E、F过AC中点O,交AD、BC于E、F,求证:OE=OF.
ABCD
A
B
C
D
E
F
O
1.在 ABCD中,∠A= ,则∠B= °,∠D= °
2.如果 ABCD中,∠A+∠C=240°,则∠A= °,
∠B= °.
3.如果 ABCD的周长为28cm,且AB:BC=2∶5,那么
AB= cm,BC= cm,CD= cm,CD= cm.
基础训练
4.已知O是 ABCD的对角线交点,
AC=10cm,BD=18cm,AD=12cm,
则△BOC的周长是_____.
O
B
A
C
D
4
60
120
10
4
10
26
130
130
6.达标评价
有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm、BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
6.学以致用
A
C
D
B
O
●
老大
老四
老三
老二
M
故四人的土地面积相同,老人分地合理。
研究对象 研究结果 几何表示法
边 对边
邻边
角 对角
邻角
对角线
A
D
C
B
平行且相等
相等
互补
∠A=∠C,∠B=∠D
AB∥CD,AD∥BC
=
=
∠A+∠B=180°(略)
互相平分
AO=CO , BO=DO
O
B
A
C
D
邻边之和相等
AB+BC=AD+DC
19.1 平行四边形的性质
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
平行四边形不相邻的两个顶点连成的线段叫它的对角线.
学习平行四边形的定义
1.
2.探讨平行四边形的性质
1) 如图,在方格纸上有A、B、C三点,请画出以这三点为顶点的平行四边形。
通过画图,试写出平行四边形的关于边、角、对角线的结论。
D
O
2)如图,在方格纸上有A、B、C三点,请画出以这三点为顶点的平行四边形。
通过画图,试写出平行四边形的关于边、角、对角线的结论。
O
D
3)如图,在方格纸上有A、B、C三点,请画出以这三点为顶点的平行四边形。
通过画图,试写出平行四边形的关于边、角、对角线的结论。
O
D
1)已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
2)已知:如图,在平行四边形 ABCD中,
求证:AB=CD,AD=BC,
证明:连接AC, ABCD中
∵ AB∥CD,AD∥BC,
∴ ∠1=∠3,∠2=∠4.
又 AC=CA,
∴ △ABC≌△CDA (ASA)
∴ AB=CD,CB=AD,
A
D
C
B
1
4
2
3
3)已知:如图,在平行四边形 ABCD中,
求证:∠A=∠C, ∠B=∠D
证明:连接AC, ABCD中
∵ AB∥CD,AD∥BC,
∴ ∠1=∠3,∠2=∠4.
又 AC=CA,
∴ △ABC≌△CDA (ASA)
∴ ∠B=∠D.
又∵ ∠1+∠4=∠2+∠3,
∴ ∠BAD=∠BCD.
A
D
C
B
1
4
2
3
4)已知:如图,在平行四边形 ABCD中,
求证:∠A=∠C, ∠B=∠D
证明: ABCD中
∵ AB∥CD,AD∥BC,
∴ ∠A+ ∠D =180°,
∠A+∠B=180°
∴∠ D=∠ B,
同理:
∠A+ ∠D =180°,
∠C+∠D=180°,
∴∠A= ∠C
A
D
C
B
5)如图:在 ABCD中,AC与BD相交
与点O。
求证:OA=OC OB=OD
1
4
2
3
A
D
C
B
o
证明: ABCD中
∵ AD∥BC,
∴ ∠1=∠3,∠2=∠4.
又 AD=BC,
∴ △BOC≌△DOA(ASA)
∴ OA=OC OB=OD
研究对象 研究结果 几何表示法
边 对边
邻边
角 对角
邻角
对角线
3. 归纳平行四边形的性质
A
D
C
B
平行且相等
相等
互补
∠A=∠C,∠B=∠D
AB∥CD,AD∥BC
=
=
∠A+∠B=180°(略)
互相平分
AO=CO , BO=DO
O
B
A
C
D
邻边之和相等
AB+BC=AD+DC
例 1、如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m.
⑵ 若∠A+∠C=200°,
则∠A和∠B分别为多少度?
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC.
∵AB=8,
∴CD=8(m),
又AB+BC+CD+AD=36, ∴AD=BC=10(m).
解:∵四边形ABCD是平行四边形,
∴∠A=∠C, ∠A+∠B=180°.
∵∠A+∠C=200°,
∴∠A=100°,∠B=80°.
⑴ 其他三条边各长多少?
4.例题赏析
例2,如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长以及 ABCD的面积.
8
10
B
C
D
A
●
O
解:
∴△ABC是直角三角形
又∵AC⊥BC
∵四边形ABCD是平行四边形
∴BC=AD=8,CD=AB=10
又∵OA=OC
∴
∴
∴S = BC×AC=8×6=48
ABCD
1)在 ABCD中, AB=3cm,BC=8cm,则 ABCD的周长
是 cm.
2) ABCD的周长为30cm,两邻边之比为2﹕1,则 ABCD
的两邻边长分别为 .
3) ABCD的周长为30cm,AB比BC长5cm,则AB= cm,
CD= cm.
4)如图,在 ABCD中,∠B的平分线BE
交AD于E,BC=5,AB=3,则ED的长为 .
5)在 ABCD中,已知∠A=130°,则∠B=__ ,
∠C=___ ,∠D=__.
(第4题)
22
10cm,5cm
2
10
10
5. 练习反馈
50°
130°
50°
6) 中,E、F过AC中点O,交AD、BC于E、F,求证:OE=OF.
ABCD
A
B
C
D
E
F
O
1.在 ABCD中,∠A= ,则∠B= °,∠D= °
2.如果 ABCD中,∠A+∠C=240°,则∠A= °,
∠B= °.
3.如果 ABCD的周长为28cm,且AB:BC=2∶5,那么
AB= cm,BC= cm,CD= cm,CD= cm.
基础训练
4.已知O是 ABCD的对角线交点,
AC=10cm,BD=18cm,AD=12cm,
则△BOC的周长是_____.
O
B
A
C
D
4
60
120
10
4
10
26
130
130
6.达标评价
有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm、BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
6.学以致用
A
C
D
B
O
●
老大
老四
老三
老二
M
故四人的土地面积相同,老人分地合理。
研究对象 研究结果 几何表示法
边 对边
邻边
角 对角
邻角
对角线
A
D
C
B
平行且相等
相等
互补
∠A=∠C,∠B=∠D
AB∥CD,AD∥BC
=
=
∠A+∠B=180°(略)
互相平分
AO=CO , BO=DO
O
B
A
C
D
邻边之和相等
AB+BC=AD+DC
