19.1平行四边形的性质(一)
文档属性
| 名称 | 19.1平行四边形的性质(一) |  | |
| 格式 | zip | ||
| 文件大小 | 914.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-03 21:39:20 | ||
图片预览




文档简介
(共15张PPT)
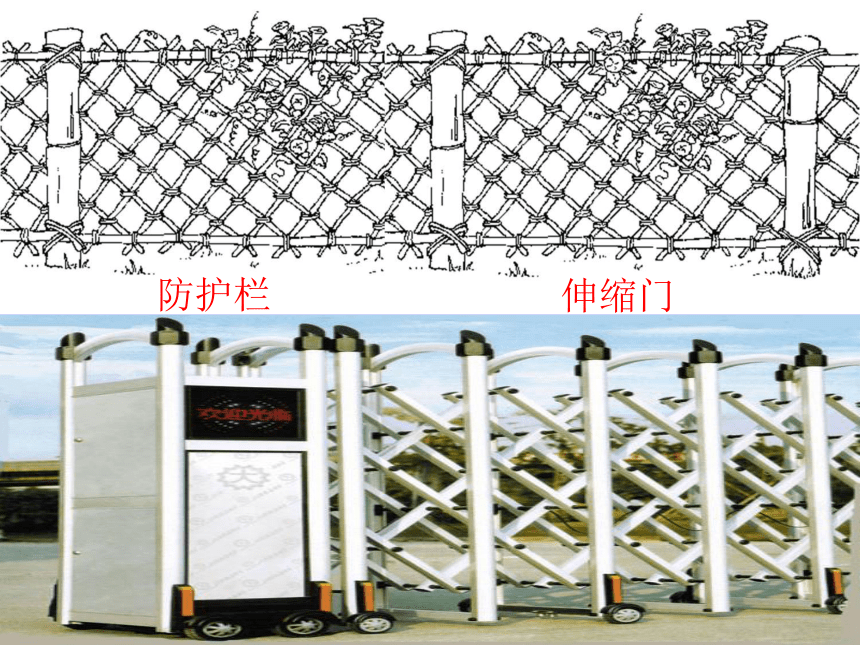
防护栏
伸缩门
同学们,通过观察这些图形,我们可以发现这些图形都具有一个共同的特点,你们能够找出吗?
想一想
这些图形都是由四边形组成
特点:
每个四边形的两组对边分别平行
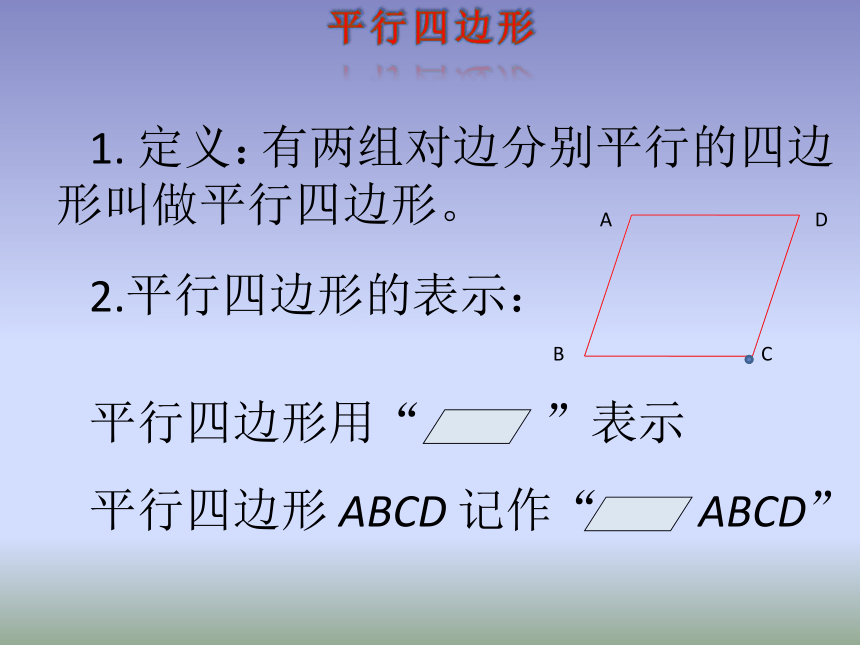
1. 定义:
有两组对边分别平行的四边形叫做平行四边形。
A
B
C
D
2.平行四边形的表示:
平行四边形用“ ”表示
平行四边形 ABCD 记作“ ABCD”
2、平行四边形不相邻的两个顶点连成的线段叫它的对角线
线段AC.BD就是它的对角线
3、平行四边形相对的边称为对边
相对的角称为对角
A
D
C
B
探 究
根据定义画一个平行四边形,观察这个四边形,除了“两组对边分别平行”外,它的边、角之间有什么关系?
A
C
B
D
度量一下,是不是和你的猜想一致?
探 究
量一量角
开启 智慧
通过观察和度量,不难发现,平行四边形具有以下性质:
平行四边形的对边相等;
平行四边形的对角相等。
我们能否证明上面结论的正确性呢?
利用三角形的全等,可以证明上述结论
已知平行四边形一个内角的度数,你能确定其他内角的度数吗?
利用三角形的全等证明平行四边形的对边、对角相等
证明:在平行四边形ABCD中,连接AC.
又知AC是公共边
∵ AD//BC,AB//CD
∴ ∠1= ∠2, ∠3= ∠4
∴ AD=BC, AB=CD
∴ △ABC≌ △CDA
∠B= ∠D
A
C
B
D
1
3
2
4
我们可以用同样的方法证明: ∠A= ∠C
例1 如图19.1 ,
B
A
C
D
图 19.1
小明用一根36 m 长的绳子围成了一个平行四边形的场地,其中AB边长为8 m ,其他三条边的长各是多少?
解:
∴ CD=8 m
∴ AB=CD , AD=BC
又 AB+BC+CD+AD=36 m
∵ AB=8 m
∴ AD=BC=10 m
∵ 四边形 ABCD 是平行四边形
练一练
1. 已知 ABCD中,∠A=80°,你能求出其他各角的度数吗?说说你的理由。
∠C=80°
∠D=100°
∠B=100°
练一练
2. 在 ABCD 中,∠A=48°,BC=3cm,则∠B= , ∠C= ,AD= 。
我们这节课学习了那些知识?
1. 平行四边形的定义
2. 平行四边形的表示
3. 平行四边形的性质:
有两组对边分别平行的四边形
用“ ”表示,平行四边形ABCD记作“ ABCD”
平行四边形的对边相等
平行四边形的对角相等
平行四边形的对边平行且相等
平行四边形的邻角呢,有怎样的关系?
平行四边形的邻角互补
作业
P84 练习题1,2 ,3
习题19.1 1 ,2 题
防护栏
伸缩门
同学们,通过观察这些图形,我们可以发现这些图形都具有一个共同的特点,你们能够找出吗?
想一想
这些图形都是由四边形组成
特点:
每个四边形的两组对边分别平行
1. 定义:
有两组对边分别平行的四边形叫做平行四边形。
A
B
C
D
2.平行四边形的表示:
平行四边形用“ ”表示
平行四边形 ABCD 记作“ ABCD”
2、平行四边形不相邻的两个顶点连成的线段叫它的对角线
线段AC.BD就是它的对角线
3、平行四边形相对的边称为对边
相对的角称为对角
A
D
C
B
探 究
根据定义画一个平行四边形,观察这个四边形,除了“两组对边分别平行”外,它的边、角之间有什么关系?
A
C
B
D
度量一下,是不是和你的猜想一致?
探 究
量一量角
开启 智慧
通过观察和度量,不难发现,平行四边形具有以下性质:
平行四边形的对边相等;
平行四边形的对角相等。
我们能否证明上面结论的正确性呢?
利用三角形的全等,可以证明上述结论
已知平行四边形一个内角的度数,你能确定其他内角的度数吗?
利用三角形的全等证明平行四边形的对边、对角相等
证明:在平行四边形ABCD中,连接AC.
又知AC是公共边
∵ AD//BC,AB//CD
∴ ∠1= ∠2, ∠3= ∠4
∴ AD=BC, AB=CD
∴ △ABC≌ △CDA
∠B= ∠D
A
C
B
D
1
3
2
4
我们可以用同样的方法证明: ∠A= ∠C
例1 如图19.1 ,
B
A
C
D
图 19.1
小明用一根36 m 长的绳子围成了一个平行四边形的场地,其中AB边长为8 m ,其他三条边的长各是多少?
解:
∴ CD=8 m
∴ AB=CD , AD=BC
又 AB+BC+CD+AD=36 m
∵ AB=8 m
∴ AD=BC=10 m
∵ 四边形 ABCD 是平行四边形
练一练
1. 已知 ABCD中,∠A=80°,你能求出其他各角的度数吗?说说你的理由。
∠C=80°
∠D=100°
∠B=100°
练一练
2. 在 ABCD 中,∠A=48°,BC=3cm,则∠B= , ∠C= ,AD= 。
我们这节课学习了那些知识?
1. 平行四边形的定义
2. 平行四边形的表示
3. 平行四边形的性质:
有两组对边分别平行的四边形
用“ ”表示,平行四边形ABCD记作“ ABCD”
平行四边形的对边相等
平行四边形的对角相等
平行四边形的对边平行且相等
平行四边形的邻角呢,有怎样的关系?
平行四边形的邻角互补
作业
P84 练习题1,2 ,3
习题19.1 1 ,2 题
