19.1平行四边形的判定(一)
文档属性
| 名称 | 19.1平行四边形的判定(一) |  | |
| 格式 | zip | ||
| 文件大小 | 328.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-03 21:42:57 | ||
图片预览



文档简介
(共11张PPT)
X
班 级:八(2)
教 师:王 余
飞鱼工作室制作
我们前面学行四边形的性质,那么平行四边形有哪些性质呢?
回 顾
平行四边形的对边相等
平行四边形的对角线平分
平行四边形的对角相等
我们能否将上面这些性质写成命题呢?
如果将这些命题作为原命题,那么它的逆命题又是什么,是否成立?
思 考
如果一个四边形是平行四边形,那么这个四边形的对边相等
逆命题:如果一个四边形的对边相等,那么这个四边形是平行四边形
如果一个四边形是平行四边形,那么这个四边形的对角相等
逆命题:如果一个四边形的对角相等,那么这个四边形是平行四边形
如果一个四边形是平行四边形,那么这个四边形的对边相等
逆命题:如果一个四边形的对角相等,那么这个四边形是平行四边形
探 究
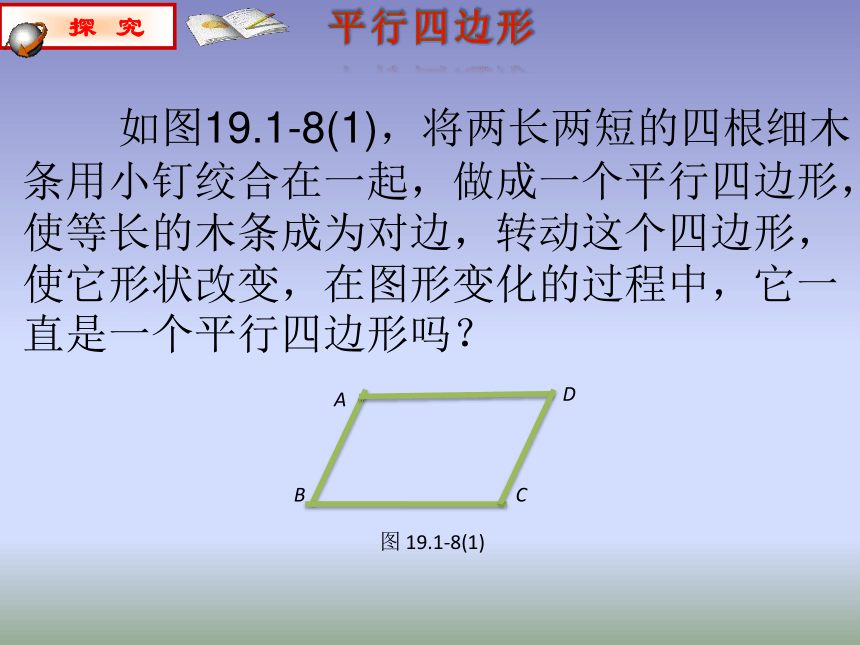
如图19.1-8(1),将两长两短的四根细木条用小钉绞合在一起,做成一个平行四边形,使等长的木条成为对边,转动这个四边形,使它形状改变,在图形变化的过程中,它一直是一个平行四边形吗?
B
A
C
D
图 19.1-8(1)
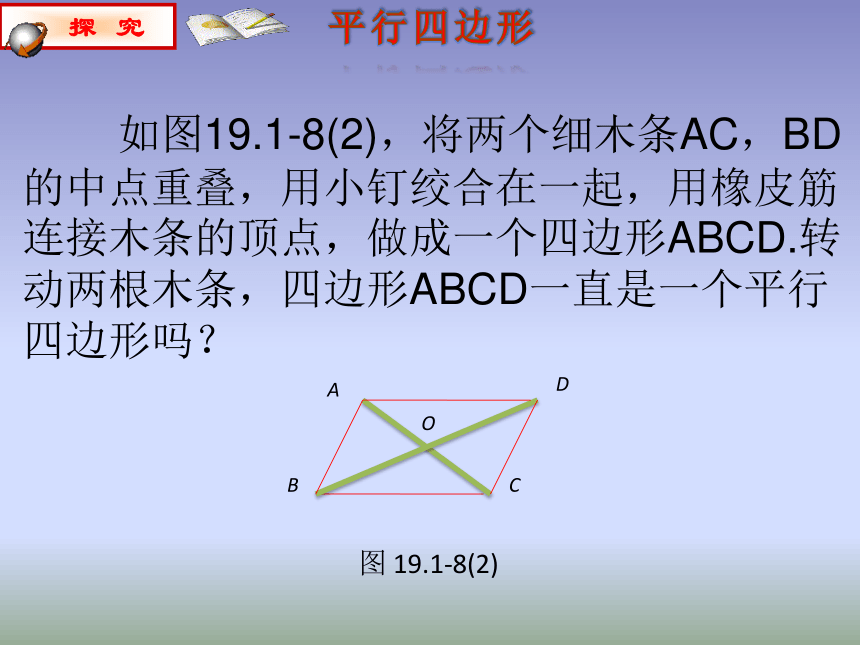
如图19.1-8(2),将两个细木条AC,BD的中点重叠,用小钉绞合在一起,用橡皮筋连接木条的顶点,做成一个四边形ABCD.转动两根木条,四边形ABCD一直是一个平行四边形吗?
探 究
B
A
C
D
图 19.1-8(2)
O
求 证
求证:
∴ △ ABC ≌ △ ACD
(SSS)
证明:
已知:
∵ AB=CD,AD=BC
四边形ABCD是平行四边形
在四边形ABCD中,AB=CD,AD=BC
A
D
B
C
连接AC
(平行四边形的定义)
∴ ∠ACB = ∠CAD
∠BAC= ∠DCA
∴ AD // BC
AB // CD
∴ 四边形ABCD是平行四边形
AC是△ ABC和△ ACD的公共边
练一练
已知:四边形ABCD,对角线AB、CD相交于点O且OA = OC,OB = OD
求证:四边形ABCD是平行四边形
A
D
B
C
O
已知:在四边形ABCD中, ∠A = ∠C, ∠B = ∠D
求证:四边形ABCD是平行四边形
A
D
B
C
利用三角形的全等证明(SAS)
四边形的内角和等于3600
同旁内角互补,两直线平行
证明:
∵ 四边形ABCD是平行四边形
∴ 四边形BFDE是平行四边形
∴ AO= CO,BO=DO
∴ EO=FO
∵ AE=CF
例3 如图19.1-9,ABCD的对角线AC,BD相交于点O,点E、F是AC上的两点,并且AE=CF,求证:四边形BFDE是平行四边形.
又 BO=DO
A
D
B
C
O
E
F
图19.1-9
这节课我们学行四边形的判定,它都有哪些判定定理呢?
平行四边形的判定定理:
2. 对角线互相平分的四边形是平行四边形
1. 两组对边分别相等的四边形是平行四边形
文字语言 图形语言 符号语言
定义判定
判定定理1
判定定理2
推论
两组对边分别平行的四边形是平行四边形
对角线互相平分的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
A
D
B
C
A
D
B
C
A
D
B
C
∵ AB//CD,AD//BC
∴ 四边形ABCD是平行四边形
∵ AB=CD,AD=BC
∵ OA=OC,OB=OD
∵∠A = ∠C,∠B = ∠D
∴ 四边形ABCD是平行四边形
∴ 四边形ABCD是平行四边形
∴ 四边形ABCD是平行四边形
A
D
B
C
O
作业
习题19.1 4 ,5,9 题
X
班 级:八(2)
教 师:王 余
飞鱼工作室制作
我们前面学行四边形的性质,那么平行四边形有哪些性质呢?
回 顾
平行四边形的对边相等
平行四边形的对角线平分
平行四边形的对角相等
我们能否将上面这些性质写成命题呢?
如果将这些命题作为原命题,那么它的逆命题又是什么,是否成立?
思 考
如果一个四边形是平行四边形,那么这个四边形的对边相等
逆命题:如果一个四边形的对边相等,那么这个四边形是平行四边形
如果一个四边形是平行四边形,那么这个四边形的对角相等
逆命题:如果一个四边形的对角相等,那么这个四边形是平行四边形
如果一个四边形是平行四边形,那么这个四边形的对边相等
逆命题:如果一个四边形的对角相等,那么这个四边形是平行四边形
探 究
如图19.1-8(1),将两长两短的四根细木条用小钉绞合在一起,做成一个平行四边形,使等长的木条成为对边,转动这个四边形,使它形状改变,在图形变化的过程中,它一直是一个平行四边形吗?
B
A
C
D
图 19.1-8(1)
如图19.1-8(2),将两个细木条AC,BD的中点重叠,用小钉绞合在一起,用橡皮筋连接木条的顶点,做成一个四边形ABCD.转动两根木条,四边形ABCD一直是一个平行四边形吗?
探 究
B
A
C
D
图 19.1-8(2)
O
求 证
求证:
∴ △ ABC ≌ △ ACD
(SSS)
证明:
已知:
∵ AB=CD,AD=BC
四边形ABCD是平行四边形
在四边形ABCD中,AB=CD,AD=BC
A
D
B
C
连接AC
(平行四边形的定义)
∴ ∠ACB = ∠CAD
∠BAC= ∠DCA
∴ AD // BC
AB // CD
∴ 四边形ABCD是平行四边形
AC是△ ABC和△ ACD的公共边
练一练
已知:四边形ABCD,对角线AB、CD相交于点O且OA = OC,OB = OD
求证:四边形ABCD是平行四边形
A
D
B
C
O
已知:在四边形ABCD中, ∠A = ∠C, ∠B = ∠D
求证:四边形ABCD是平行四边形
A
D
B
C
利用三角形的全等证明(SAS)
四边形的内角和等于3600
同旁内角互补,两直线平行
证明:
∵ 四边形ABCD是平行四边形
∴ 四边形BFDE是平行四边形
∴ AO= CO,BO=DO
∴ EO=FO
∵ AE=CF
例3 如图19.1-9,ABCD的对角线AC,BD相交于点O,点E、F是AC上的两点,并且AE=CF,求证:四边形BFDE是平行四边形.
又 BO=DO
A
D
B
C
O
E
F
图19.1-9
这节课我们学行四边形的判定,它都有哪些判定定理呢?
平行四边形的判定定理:
2. 对角线互相平分的四边形是平行四边形
1. 两组对边分别相等的四边形是平行四边形
文字语言 图形语言 符号语言
定义判定
判定定理1
判定定理2
推论
两组对边分别平行的四边形是平行四边形
对角线互相平分的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
A
D
B
C
A
D
B
C
A
D
B
C
∵ AB//CD,AD//BC
∴ 四边形ABCD是平行四边形
∵ AB=CD,AD=BC
∵ OA=OC,OB=OD
∵∠A = ∠C,∠B = ∠D
∴ 四边形ABCD是平行四边形
∴ 四边形ABCD是平行四边形
∴ 四边形ABCD是平行四边形
A
D
B
C
O
作业
习题19.1 4 ,5,9 题
