2.1:圆的对称性 课件 2020-2021学年湘教版九年级下册数学(共17张ppt)
文档属性
| 名称 | 2.1:圆的对称性 课件 2020-2021学年湘教版九年级下册数学(共17张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 9.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-06 21:01:18 | ||
图片预览


文档简介
第二章 圆
一石激起千层浪
奥运五环
乐在其中
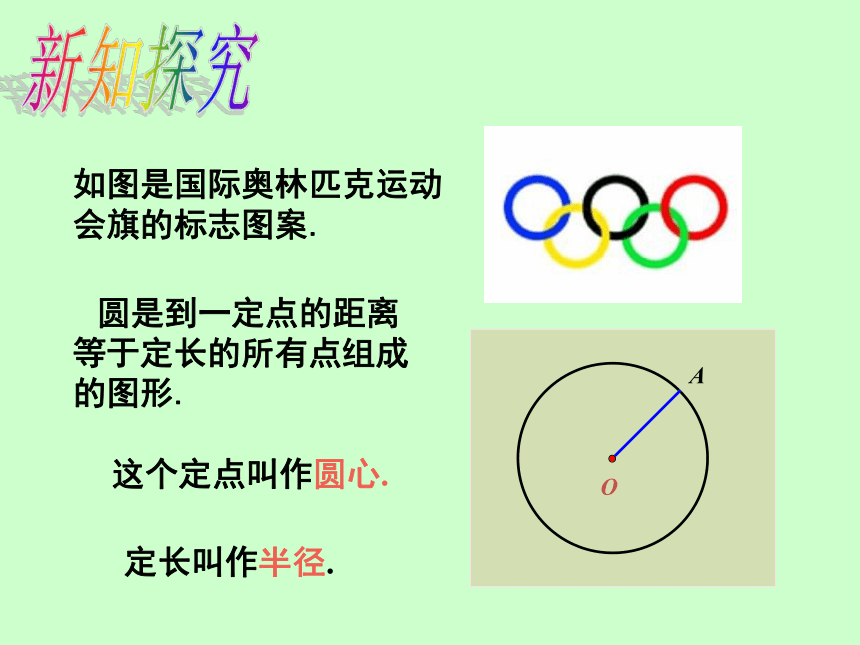
如图是国际奥林匹克运动会旗的标志图案.
圆是到一定点的距离等于定长的所有点组成的图形.
·
定长叫作半径.
这个定点叫作圆心.
O
A
·
O
A
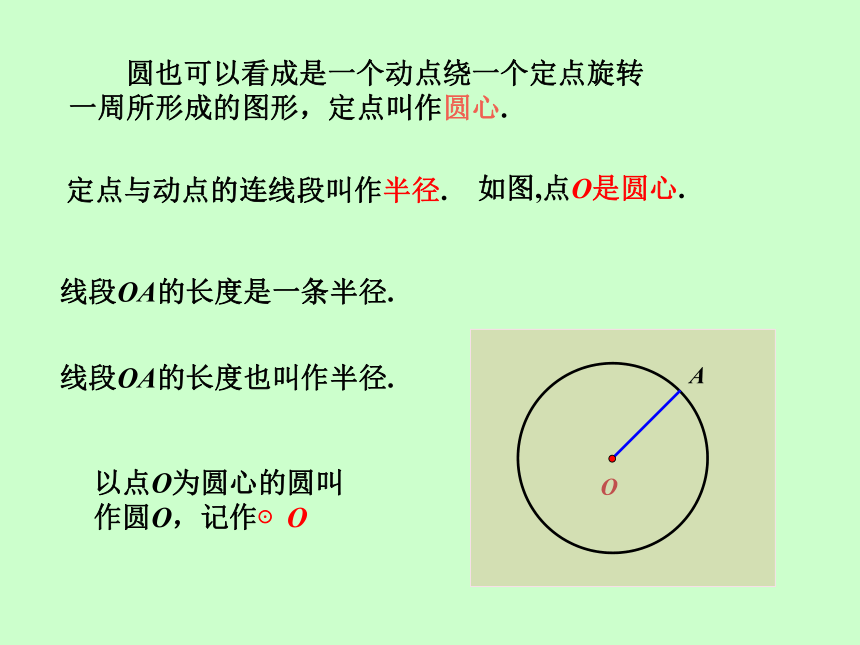
圆也可以看成是一个动点绕一个定点旋转一周所形成的图形,定点叫作圆心.
以点O为圆心的圆叫作圆O,记作⊙O
定点与动点的连线段叫作半径.
如图,点O是圆心.
线段OA的长度是一条半径.
线段OA的长度也叫作半径.
r
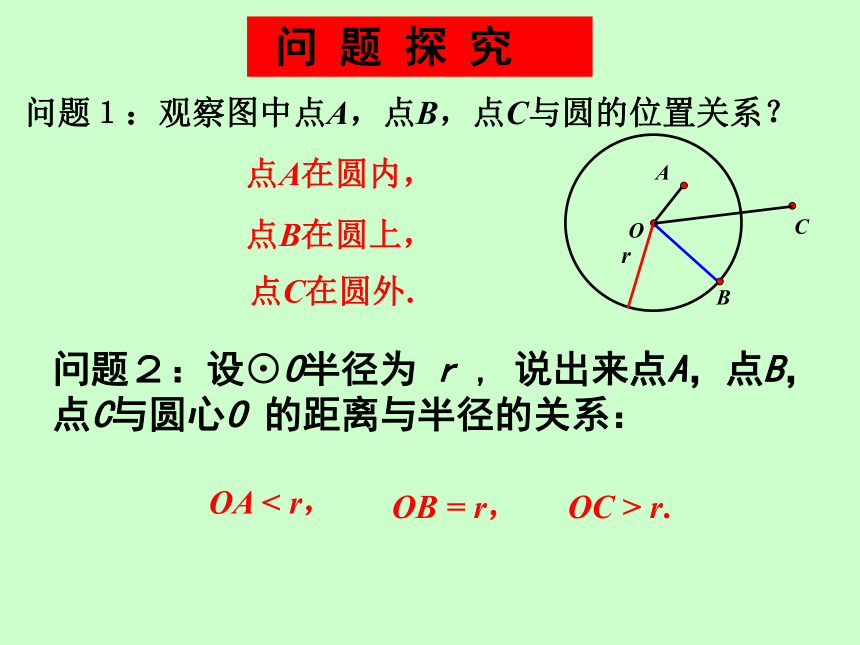
问题2:设⊙O半径为 r , 说出来点A,点B,点C与圆心O 的距离与半径的关系:
·
C
O
A
B
OC > r.
问题1:观察图中点A,点B,点C与圆的位置关系?
点C在圆外.
点A在圆内,
点B在圆上,
OA < r,
OB = r,
问 题 探 究
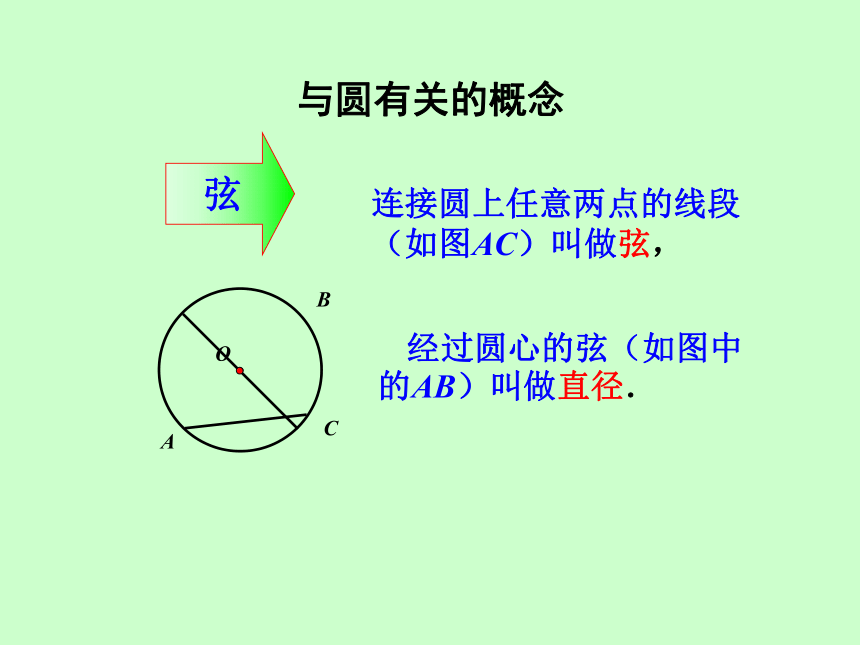
经过圆心的弦(如图中的AB)叫做直径.
·
C
O
A
B
连接圆上任意两点的线段(如图AC)叫做弦,
与圆有关的概念
弦
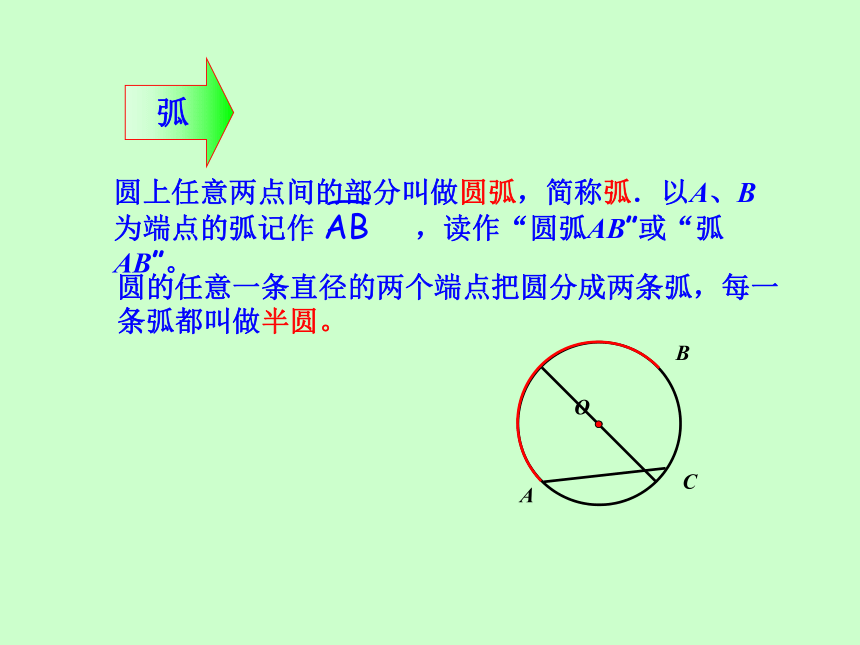
圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作 ,读作“圆弧AB”或“弧AB”。
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆。
·
C
O
A
B
弧
AB
大于半圆的弧(用三个字母表示,如图中的 )叫做优弧。
小于半圆的弧(如图中的 )叫做劣弧;
·
C
O
A
B
劣弧与优弧
AC
ABC
这两个圆
1、用一块硬纸板和一张薄的白纸分别画一个圆,它们的半径相等,把白纸放在硬纸板上面,使两个圆的圆心重合,观察这两个圆是否重合?
做
一
做
能够重合的两个圆叫作相等的圆,或等圆
重合
现在用一根大头针穿过这两个圆的圆心,让硬纸板保持不动,让白纸绕圆心旋转任意角度,观察旋转后,白纸上的圆是否仍然与硬纸板上的圆重合?
这体现圆具有什么样的性质?
……
……
圆是旋转对称图形,即圆绕圆心旋转任意角度,都能与自身重合.特别地,圆是中心对称图形,圆心是它的对称中心.
·
2、在白纸的圆上面画任意一条直径,把白纸沿着这条直径所在的直线折叠.观察圆的两部分是否互相重合?
·
O
A
B
C
D
E
这体现圆具有什么样的对称性?
……
你能讲出圆具有这种对称性的道理吗?
圆是轴对称图形是任意一条直径所在的直线,都是圆的对称轴.
……
圆的对称性
圆是轴对称图形.
圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.
可利用折叠的方法即可解决上述问题.
圆也是中心对称图形.
它的对称中心就是圆心.
用旋转的方法即可解决这个问题.
议一议:为什么通常要把车轮设计为圆形?
把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变,因此,当车辆在平坦的路上行驶时,坐车的人会感觉到非常平稳,这也是车轮都做成圆形的数学道理.
1.判断题
(1)直径是弦 . (2)过圆心的线段是直径.
(3)半圆是弧 . (4)两个半圆是等弧.
(5)面积不等的两圆不是等圆.
(6)长度相等的两条弧是等弧.
A
C
E
F
G
H
弧长
FE
=
3.84 cm
弧长
HG
=
3.84 cm
(√)
(×)
(√)
(×)
(√)
(×)
1.圆的概念
2.与圆有关的概念
弦,直径,弧(优弧和劣弧)
成功=艰苦劳动+正确方法+少说空话。
——爱因斯坦
一石激起千层浪
奥运五环
乐在其中
如图是国际奥林匹克运动会旗的标志图案.
圆是到一定点的距离等于定长的所有点组成的图形.
·
定长叫作半径.
这个定点叫作圆心.
O
A
·
O
A
圆也可以看成是一个动点绕一个定点旋转一周所形成的图形,定点叫作圆心.
以点O为圆心的圆叫作圆O,记作⊙O
定点与动点的连线段叫作半径.
如图,点O是圆心.
线段OA的长度是一条半径.
线段OA的长度也叫作半径.
r
问题2:设⊙O半径为 r , 说出来点A,点B,点C与圆心O 的距离与半径的关系:
·
C
O
A
B
OC > r.
问题1:观察图中点A,点B,点C与圆的位置关系?
点C在圆外.
点A在圆内,
点B在圆上,
OA < r,
OB = r,
问 题 探 究
经过圆心的弦(如图中的AB)叫做直径.
·
C
O
A
B
连接圆上任意两点的线段(如图AC)叫做弦,
与圆有关的概念
弦
圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作 ,读作“圆弧AB”或“弧AB”。
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆。
·
C
O
A
B
弧
AB
大于半圆的弧(用三个字母表示,如图中的 )叫做优弧。
小于半圆的弧(如图中的 )叫做劣弧;
·
C
O
A
B
劣弧与优弧
AC
ABC
这两个圆
1、用一块硬纸板和一张薄的白纸分别画一个圆,它们的半径相等,把白纸放在硬纸板上面,使两个圆的圆心重合,观察这两个圆是否重合?
做
一
做
能够重合的两个圆叫作相等的圆,或等圆
重合
现在用一根大头针穿过这两个圆的圆心,让硬纸板保持不动,让白纸绕圆心旋转任意角度,观察旋转后,白纸上的圆是否仍然与硬纸板上的圆重合?
这体现圆具有什么样的性质?
……
……
圆是旋转对称图形,即圆绕圆心旋转任意角度,都能与自身重合.特别地,圆是中心对称图形,圆心是它的对称中心.
·
2、在白纸的圆上面画任意一条直径,把白纸沿着这条直径所在的直线折叠.观察圆的两部分是否互相重合?
·
O
A
B
C
D
E
这体现圆具有什么样的对称性?
……
你能讲出圆具有这种对称性的道理吗?
圆是轴对称图形是任意一条直径所在的直线,都是圆的对称轴.
……
圆的对称性
圆是轴对称图形.
圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.
可利用折叠的方法即可解决上述问题.
圆也是中心对称图形.
它的对称中心就是圆心.
用旋转的方法即可解决这个问题.
议一议:为什么通常要把车轮设计为圆形?
把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变,因此,当车辆在平坦的路上行驶时,坐车的人会感觉到非常平稳,这也是车轮都做成圆形的数学道理.
1.判断题
(1)直径是弦 . (2)过圆心的线段是直径.
(3)半圆是弧 . (4)两个半圆是等弧.
(5)面积不等的两圆不是等圆.
(6)长度相等的两条弧是等弧.
A
C
E
F
G
H
弧长
FE
=
3.84 cm
弧长
HG
=
3.84 cm
(√)
(×)
(√)
(×)
(√)
(×)
1.圆的概念
2.与圆有关的概念
弦,直径,弧(优弧和劣弧)
成功=艰苦劳动+正确方法+少说空话。
——爱因斯坦
