沪科版数学七年级下册期末综合测评卷(三)(含答案)
文档属性
| 名称 | 沪科版数学七年级下册期末综合测评卷(三)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-04 13:18:36 | ||
图片预览



文档简介
沪科版数学七年级下册期末综合测评卷(三)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.若M,N都是实数,且M=,N=,则M,N的大小关系是 ( )
A.M>N B.M≥N
C.M2.若a,b为有理数,且2a2-2ab+b2+4a+4=0,则a2b+ab2( )
A.-8 B.-16 C.8 D.16
3.下列运算正确的是( D )
A.x2·x3=x6 B.x2+x3=x5
C.(-x2)4=x6 D.x6÷x5=x
4.某种细胞的直径是0.00000095米,将0.00000095用科学记数法表示为( )
A.9.5×10-7 B.9.5×10-8
C.0.95×10-7 D.95×10-8
5.不等式x-3≤3x+1的解集在数轴上表示正确的是( )
6.如图,能判定EB∥AC的条件是( )
A.∠A=∠ABE B.∠A=∠EBD
C.∠C=∠ABC D.∠C=∠ABE
7.下列叙述正确的是( )
A.4的平方根是2 B.16的算术平方根是4
C.-27没有立方根 D.是无理数
8.若关于x的分式方程=2有增根,则m的值是( )
A.-1 B.0
C.3 D.0或3
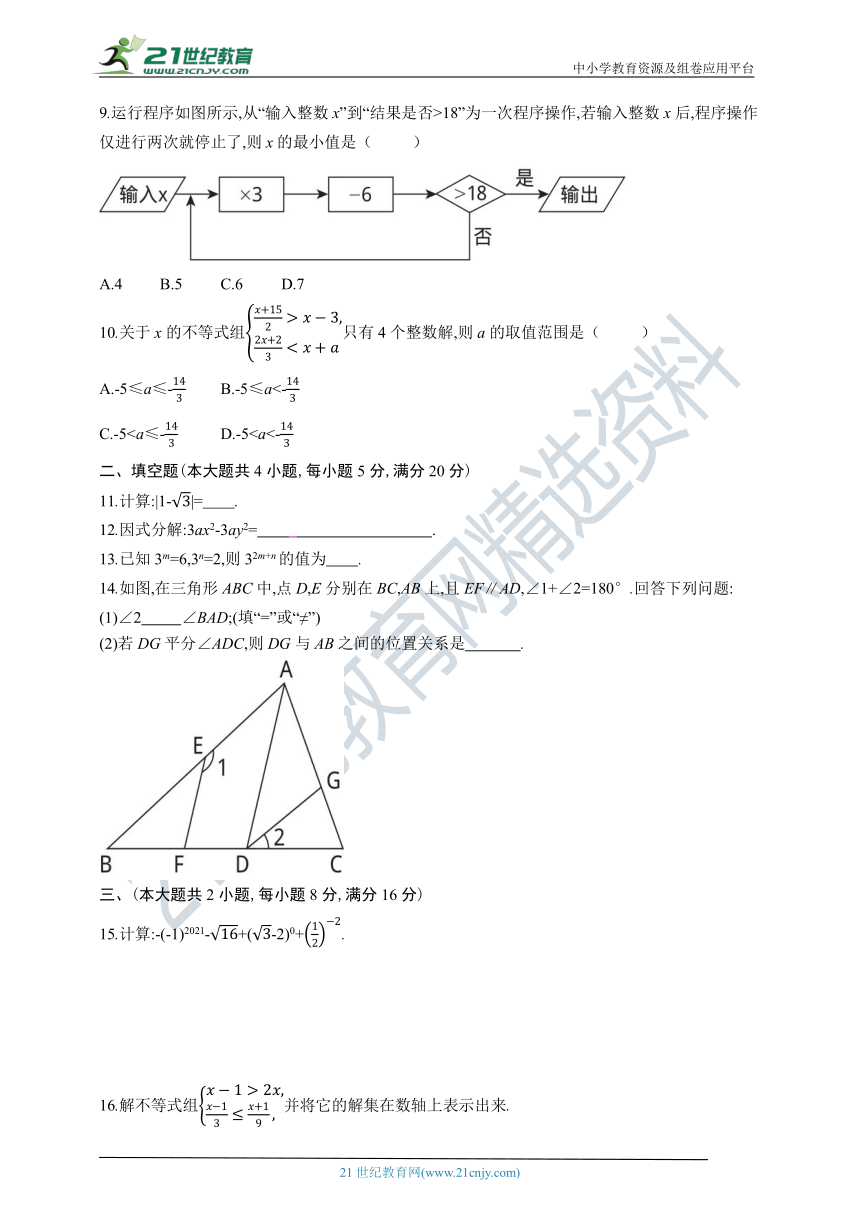
9.运行程序如图所示,从“输入整数x”到“结果是否>18”为一次程序操作,若输入整数x后,程序操作仅进行两次就停止了,则x的最小值是( )
A.4 B.5 C.6 D.7
10.关于x的不等式组只有4个整数解,则a的取值范围是( )
A.-5≤a≤- B.-5≤a<-
C.-5二、填空题(本大题共4小题,每小题5分,满分20分)
11.计算:|1-|= .
12.因式分解:3ax2-3ay2= .
13.已知3m=6,3n=2,则32m+n的值为 .
14.如图,在三角形ABC中,点D,E分别在BC,AB上,且EF∥AD,∠1+∠2=180°.回答下列问题:
(1)∠2 ∠BAD;(填“=”或“≠”)
(2)若DG平分∠ADC,则DG与AB之间的位置关系是 .
三、(本大题共2小题,每小题8分,满分16分)
15.计算:-(-1)2021-+(-2)0+.
16.解不等式组并将它的解集在数轴上表示出来.
四、(本大题共2小题,每小题8分,满分16分)
17.计算:(x+3)(x+4)-(x-1)2.
18.为有效开展“阳光体育”活动,某校计划购买篮球和足球共50个,购买资金不超过3000元.若每个篮球80元,每个足球50元,求篮球最多可购买多少个
五、(本大题共2小题,每小题10分,满分20分)
19.在如图所示的正方形网格中,每个小正方形的边长都为1个单位长度,三角形ABC的顶点都在正方形网格的格点上,将三角形ABC向上平移m个单位长度,再向右平移n个单位长度,平移后得到三角形A'B'C',其中图中直线l上的点A'是点A的对应点.
(1)画出平移后得到的三角形A'B'C';
(2)m+n= ;
(3)在直线l上存在一点D,使A',B',C',D所围成的四边形的面积为6,请在直线l上画出所有符合要求的格点D.
20.先化简:,再请从-2,-1,0,1中选一个你认为合适的数作为x的值,代入求值.
六、(满分12分)
21.我们在解题时,经常会遇到“数的平方”,那么你有简便方法吗 这里,我们以“两位数的平方”为例,请观察下列各式的规律,回答问题:
262=(26+6)×20+62;
372=(37+7)×30+72;
432=(43+3)×40+32;
…
(1)请根据上述规律填空:682= .
(2)我们知道,任何一个两位数(个数上的数字为n,十位上的数字为m)都可以表示为10m+n,根据上述规律写出:(10m+n)2= ,并用所学知识说明你的结论的正确性.
(3)利用上述结论,简便计算982.
七、(满分12分)
22.为抗击新型冠状病毒肺炎疫情,某公司承担生产8800万个口罩的任务,该公司有A,B两个生产口罩的车间,A车间每天生产的口罩数量是B车间的1.2倍,A,B两车间共同生产一半后,A车间被抽调生产其他急需用品,剩下的全部由B车间单独完成,结果前后共用16天完成.
(1)求A,B两车间每天分别能生产口罩多少万个
(2)如果A车间每生产1万个口罩可创造利润1.5万元,B车间每生产1万个口罩可创造利润1.2万元,求该公司生产这批口罩共创造利润多少万元
八、(满分14分)
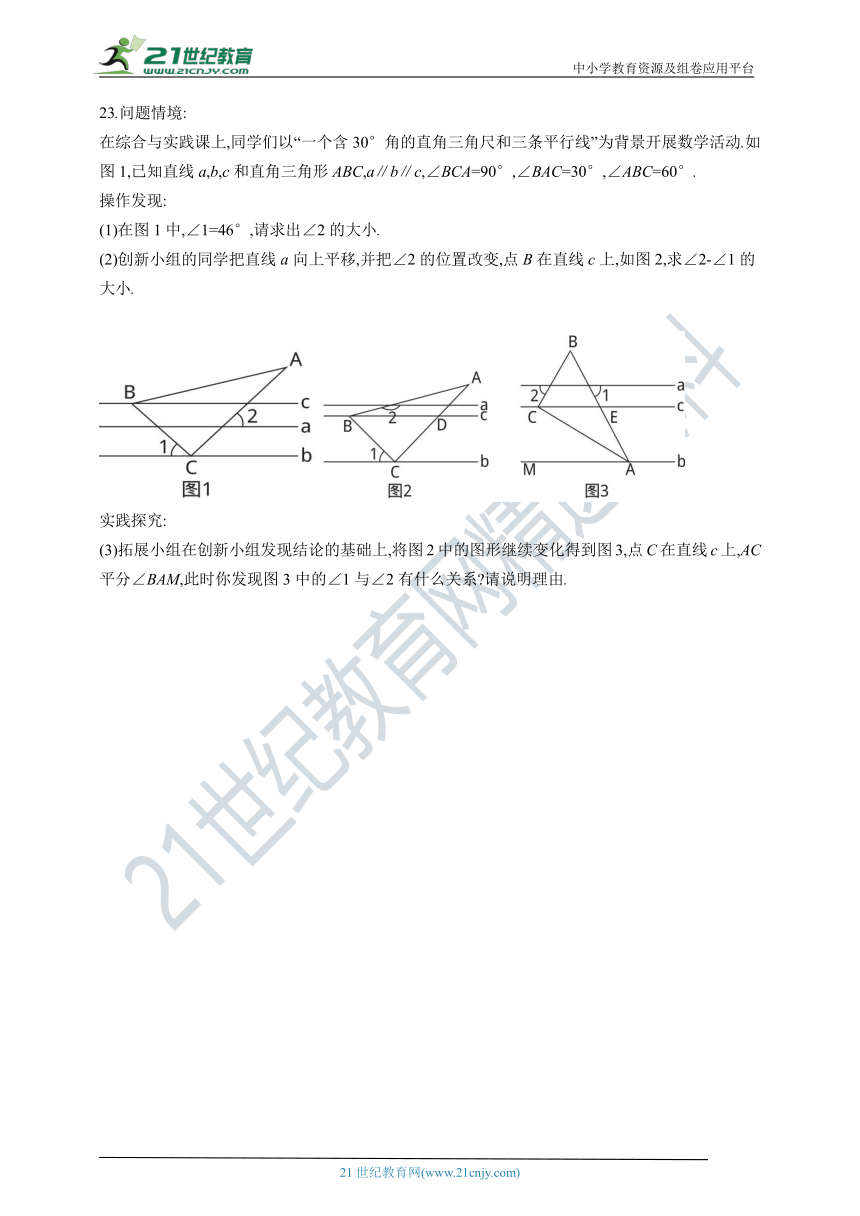
23.问题情境:
在综合与实践课上,同学们以“一个含30°角的直角三角尺和三条平行线”为背景开展数学活动.如图1,已知直线a,b,c和直角三角形ABC,a∥b∥c,∠BCA=90°,∠BAC=30°,∠ABC=60°.
操作发现:
(1)在图1中,∠1=46°,请求出∠2的大小.
(2)创新小组的同学把直线a向上平移,并把∠2的位置改变,点B在直线c上,如图2,求∠2-∠1的大小.
实践探究:
(3)拓展小组在创新小组发现结论的基础上,将图2中的图形继续变化得到图3,点C在直线c上,AC平分∠BAM,此时你发现图3中的∠1与∠2有什么关系 请说明理由.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
1.若M,N都是实数,且M=,N=,则M,N的大小关系是 ( D )
A.M>N B.M≥N
C.M2.若a,b为有理数,且2a2-2ab+b2+4a+4=0,则a2b+ab2( B )
A.-8 B.-16 C.8 D.16
3.下列运算正确的是( D )
A.x2·x3=x6 B.x2+x3=x5
C.(-x2)4=x6 D.x6÷x5=x
4.某种细胞的直径是0.00000095米,将0.00000095用科学记数法表示为( A )
A.9.5×10-7 B.9.5×10-8
C.0.95×10-7 D.95×10-8
5.不等式x-3≤3x+1的解集在数轴上表示正确的是( D )
6.如图,能判定EB∥AC的条件是( A )
A.∠A=∠ABE B.∠A=∠EBD
C.∠C=∠ABC D.∠C=∠ABE
7.下列叙述正确的是( B )
A.4的平方根是2 B.16的算术平方根是4
C.-27没有立方根 D.是无理数
8.若关于x的分式方程=2有增根,则m的值是( A )
A.-1 B.0
C.3 D.0或3
9.运行程序如图所示,从“输入整数x”到“结果是否>18”为一次程序操作,若输入整数x后,程序操作仅进行两次就停止了,则x的最小值是( B )
A.4 B.5 C.6 D.7
10.关于x的不等式组只有4个整数解,则a的取值范围是( C )
A.-5≤a≤- B.-5≤a<-
C.-5【解析】不等式组的解集是2-3a二、填空题(本大题共4小题,每小题5分,满分20分)
11.计算:|1-|= -1 .
12.因式分解:3ax2-3ay2= 3a(x+y)(x-y) .
【答案】3a(x+y)(x-y).
【解析】解:3ax2-3ay2=3a(x2-y2)=3a(x+y)(x-y),
故答案为3a(x+y)(x-y).
13.已知3m=6,3n=2,则32m+n的值为 72 .
14.如图,在三角形ABC中,点D,E分别在BC,AB上,且EF∥AD,∠1+∠2=180°.回答下列问题:
(1)∠2 = ∠BAD;(填“=”或“≠”)
(2)若DG平分∠ADC,则DG与AB之间的位置关系是 平行 .
三、(本大题共2小题,每小题8分,满分16分)
15.计算:-(-1)2021-+(-2)0+.
解:原式=1-4+1+4=2.
16.解不等式组并将它的解集在数轴上表示出来.
解:解不等式x-1>2x,得x<-1,
解不等式,得x≤2.
所以不等式组的解集为x<-1.
不等式组的解集在数轴上表示为:
四、(本大题共2小题,每小题8分,满分16分)
17.计算:(x+3)(x+4)-(x-1)2.
解:原式=x2+4x+3x+12-x2+2x-1=9x+11.
18.为有效开展“阳光体育”活动,某校计划购买篮球和足球共50个,购买资金不超过3000元.若每个篮球80元,每个足球50元,求篮球最多可购买多少个
解:设篮球可购买m个,则足球可购买(50-m)个.
根据题意,得80m+50(50-m)≤3000,
解得m≤16.
因为m为正整数,所以m的最大值为16.
答:篮球最多可购买16个.
五、(本大题共2小题,每小题10分,满分20分)
19.在如图所示的正方形网格中,每个小正方形的边长都为1个单位长度,三角形ABC的顶点都在正方形网格的格点上,将三角形ABC向上平移m个单位长度,再向右平移n个单位长度,平移后得到三角形A'B'C',其中图中直线l上的点A'是点A的对应点.
(1)画出平移后得到的三角形A'B'C';
(2)m+n= 8 ;
(3)在直线l上存在一点D,使A',B',C',D所围成的四边形的面积为6,请在直线l上画出所有符合要求的格点D.
解:(1)如图所示,三角形A'B'C'即为所求.
(3)如图所示,点D即为所求.
20.先化简:,再请从-2,-1,0,1中选一个你认为合适的数作为x的值,代入求值.
解:.
因为x≠±1且x≠-2,所以x=0,
所以原式=-1.
六、(满分12分)
21.我们在解题时,经常会遇到“数的平方”,那么你有简便方法吗 这里,我们以“两位数的平方”为例,请观察下列各式的规律,回答问题:
262=(26+6)×20+62;
372=(37+7)×30+72;
432=(43+3)×40+32;
…
(1)请根据上述规律填空:682= (68+8)×60+82 .
(2)我们知道,任何一个两位数(个数上的数字为n,十位上的数字为m)都可以表示为10m+n,根据上述规律写出:(10m+n)2= (10m+n+n)×10m+n2 ,并用所学知识说明你的结论的正确性.
(3)利用上述结论,简便计算982.
解:(2)证明:因为(10m+n)2=(10m)2+2×10m×n+n2=100m2+20mn+n2,
(10m+n+n)×10m+n2=100m2+20mn+n2,
所以(10m+n)2=(10m+n+n)×10m+n2.
(3)982=(98+8)×90+82=9604.
七、(满分12分)
22.为抗击新型冠状病毒肺炎疫情,某公司承担生产8800万个口罩的任务,该公司有A,B两个生产口罩的车间,A车间每天生产的口罩数量是B车间的1.2倍,A,B两车间共同生产一半后,A车间被抽调生产其他急需用品,剩下的全部由B车间单独完成,结果前后共用16天完成.
(1)求A,B两车间每天分别能生产口罩多少万个
(2)如果A车间每生产1万个口罩可创造利润1.5万元,B车间每生产1万个口罩可创造利润1.2万元,求该公司生产这批口罩共创造利润多少万元
解:(1)设B车间每天能生产口罩x万个,则A车间每天能生产口罩1.2x万个.
由题意得=16,解得x=400.
经检验,x=400是原分式方程的解,且符合题意,
所以1.2x=480.
答:A车间每天能生产口罩480万个,B车间每天能生产口罩400万个.
(2)1.2×400×16+1.5×(8800-400×16)=11280(万元).
答:该公司生产这批口罩共创造利润11280万元.
八、(满分14分)
23.问题情境:
在综合与实践课上,同学们以“一个含30°角的直角三角尺和三条平行线”为背景开展数学活动.如图1,已知直线a,b,c和直角三角形ABC,a∥b∥c,∠BCA=90°,∠BAC=30°,∠ABC=60°.
操作发现:
(1)在图1中,∠1=46°,请求出∠2的大小.
(2)创新小组的同学把直线a向上平移,并把∠2的位置改变,点B在直线c上,如图2,求∠2-∠1的大小.
实践探究:
(3)拓展小组在创新小组发现结论的基础上,将图2中的图形继续变化得到图3,点C在直线c上,AC平分∠BAM,此时你发现图3中的∠1与∠2有什么关系 请说明理由.
解:(1)如图,因为∠BCA=90°,
所以∠1+∠ACN=90°.
因为∠1=46°,所以∠ACN=90°-46°=44°.
因为a∥b,所以∠2=∠ACN=44°.
(2)因为a∥c,所以∠2+∠ABD=180°,
所以∠2=180°-∠ABD.
因为b∥c,所以∠DBC=∠1.
因为∠ABC=∠DBC+∠ABD=60°,
所以∠1+∠ABD=60°,所以∠1=60°-∠ABD,
所以∠2-∠1=180°-∠ABD-(60°-∠ABD)=120°.
(3)∠1=∠2.
理由:因为a∥c,所以∠2=∠BCE.
因为a∥b,所以∠1=∠BAM.
因为∠BAC=30°,AC平分∠BAM,
所以∠CAM=∠BAC=30°,∠BAM=2∠BAC=60°,
所以∠ECA=30°,∠1=∠BAM=60°.
因为∠BCA=90°,
所以∠2=∠BCE=90°-30°=60°,所以∠1=∠2.
一、选择题(本大题共10小题,每小题4分,满分40分)
1.若M,N都是实数,且M=,N=,则M,N的大小关系是 ( )
A.M>N B.M≥N
C.M
A.-8 B.-16 C.8 D.16
3.下列运算正确的是( D )
A.x2·x3=x6 B.x2+x3=x5
C.(-x2)4=x6 D.x6÷x5=x
4.某种细胞的直径是0.00000095米,将0.00000095用科学记数法表示为( )
A.9.5×10-7 B.9.5×10-8
C.0.95×10-7 D.95×10-8
5.不等式x-3≤3x+1的解集在数轴上表示正确的是( )
6.如图,能判定EB∥AC的条件是( )
A.∠A=∠ABE B.∠A=∠EBD
C.∠C=∠ABC D.∠C=∠ABE
7.下列叙述正确的是( )
A.4的平方根是2 B.16的算术平方根是4
C.-27没有立方根 D.是无理数
8.若关于x的分式方程=2有增根,则m的值是( )
A.-1 B.0
C.3 D.0或3
9.运行程序如图所示,从“输入整数x”到“结果是否>18”为一次程序操作,若输入整数x后,程序操作仅进行两次就停止了,则x的最小值是( )
A.4 B.5 C.6 D.7
10.关于x的不等式组只有4个整数解,则a的取值范围是( )
A.-5≤a≤- B.-5≤a<-
C.-5
11.计算:|1-|= .
12.因式分解:3ax2-3ay2= .
13.已知3m=6,3n=2,则32m+n的值为 .
14.如图,在三角形ABC中,点D,E分别在BC,AB上,且EF∥AD,∠1+∠2=180°.回答下列问题:
(1)∠2 ∠BAD;(填“=”或“≠”)
(2)若DG平分∠ADC,则DG与AB之间的位置关系是 .
三、(本大题共2小题,每小题8分,满分16分)
15.计算:-(-1)2021-+(-2)0+.
16.解不等式组并将它的解集在数轴上表示出来.
四、(本大题共2小题,每小题8分,满分16分)
17.计算:(x+3)(x+4)-(x-1)2.
18.为有效开展“阳光体育”活动,某校计划购买篮球和足球共50个,购买资金不超过3000元.若每个篮球80元,每个足球50元,求篮球最多可购买多少个
五、(本大题共2小题,每小题10分,满分20分)
19.在如图所示的正方形网格中,每个小正方形的边长都为1个单位长度,三角形ABC的顶点都在正方形网格的格点上,将三角形ABC向上平移m个单位长度,再向右平移n个单位长度,平移后得到三角形A'B'C',其中图中直线l上的点A'是点A的对应点.
(1)画出平移后得到的三角形A'B'C';
(2)m+n= ;
(3)在直线l上存在一点D,使A',B',C',D所围成的四边形的面积为6,请在直线l上画出所有符合要求的格点D.
20.先化简:,再请从-2,-1,0,1中选一个你认为合适的数作为x的值,代入求值.
六、(满分12分)
21.我们在解题时,经常会遇到“数的平方”,那么你有简便方法吗 这里,我们以“两位数的平方”为例,请观察下列各式的规律,回答问题:
262=(26+6)×20+62;
372=(37+7)×30+72;
432=(43+3)×40+32;
…
(1)请根据上述规律填空:682= .
(2)我们知道,任何一个两位数(个数上的数字为n,十位上的数字为m)都可以表示为10m+n,根据上述规律写出:(10m+n)2= ,并用所学知识说明你的结论的正确性.
(3)利用上述结论,简便计算982.
七、(满分12分)
22.为抗击新型冠状病毒肺炎疫情,某公司承担生产8800万个口罩的任务,该公司有A,B两个生产口罩的车间,A车间每天生产的口罩数量是B车间的1.2倍,A,B两车间共同生产一半后,A车间被抽调生产其他急需用品,剩下的全部由B车间单独完成,结果前后共用16天完成.
(1)求A,B两车间每天分别能生产口罩多少万个
(2)如果A车间每生产1万个口罩可创造利润1.5万元,B车间每生产1万个口罩可创造利润1.2万元,求该公司生产这批口罩共创造利润多少万元
八、(满分14分)
23.问题情境:
在综合与实践课上,同学们以“一个含30°角的直角三角尺和三条平行线”为背景开展数学活动.如图1,已知直线a,b,c和直角三角形ABC,a∥b∥c,∠BCA=90°,∠BAC=30°,∠ABC=60°.
操作发现:
(1)在图1中,∠1=46°,请求出∠2的大小.
(2)创新小组的同学把直线a向上平移,并把∠2的位置改变,点B在直线c上,如图2,求∠2-∠1的大小.
实践探究:
(3)拓展小组在创新小组发现结论的基础上,将图2中的图形继续变化得到图3,点C在直线c上,AC平分∠BAM,此时你发现图3中的∠1与∠2有什么关系 请说明理由.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
1.若M,N都是实数,且M=,N=,则M,N的大小关系是 ( D )
A.M>N B.M≥N
C.M
A.-8 B.-16 C.8 D.16
3.下列运算正确的是( D )
A.x2·x3=x6 B.x2+x3=x5
C.(-x2)4=x6 D.x6÷x5=x
4.某种细胞的直径是0.00000095米,将0.00000095用科学记数法表示为( A )
A.9.5×10-7 B.9.5×10-8
C.0.95×10-7 D.95×10-8
5.不等式x-3≤3x+1的解集在数轴上表示正确的是( D )
6.如图,能判定EB∥AC的条件是( A )
A.∠A=∠ABE B.∠A=∠EBD
C.∠C=∠ABC D.∠C=∠ABE
7.下列叙述正确的是( B )
A.4的平方根是2 B.16的算术平方根是4
C.-27没有立方根 D.是无理数
8.若关于x的分式方程=2有增根,则m的值是( A )
A.-1 B.0
C.3 D.0或3
9.运行程序如图所示,从“输入整数x”到“结果是否>18”为一次程序操作,若输入整数x后,程序操作仅进行两次就停止了,则x的最小值是( B )
A.4 B.5 C.6 D.7
10.关于x的不等式组只有4个整数解,则a的取值范围是( C )
A.-5≤a≤- B.-5≤a<-
C.-5
11.计算:|1-|= -1 .
12.因式分解:3ax2-3ay2= 3a(x+y)(x-y) .
【答案】3a(x+y)(x-y).
【解析】解:3ax2-3ay2=3a(x2-y2)=3a(x+y)(x-y),
故答案为3a(x+y)(x-y).
13.已知3m=6,3n=2,则32m+n的值为 72 .
14.如图,在三角形ABC中,点D,E分别在BC,AB上,且EF∥AD,∠1+∠2=180°.回答下列问题:
(1)∠2 = ∠BAD;(填“=”或“≠”)
(2)若DG平分∠ADC,则DG与AB之间的位置关系是 平行 .
三、(本大题共2小题,每小题8分,满分16分)
15.计算:-(-1)2021-+(-2)0+.
解:原式=1-4+1+4=2.
16.解不等式组并将它的解集在数轴上表示出来.
解:解不等式x-1>2x,得x<-1,
解不等式,得x≤2.
所以不等式组的解集为x<-1.
不等式组的解集在数轴上表示为:
四、(本大题共2小题,每小题8分,满分16分)
17.计算:(x+3)(x+4)-(x-1)2.
解:原式=x2+4x+3x+12-x2+2x-1=9x+11.
18.为有效开展“阳光体育”活动,某校计划购买篮球和足球共50个,购买资金不超过3000元.若每个篮球80元,每个足球50元,求篮球最多可购买多少个
解:设篮球可购买m个,则足球可购买(50-m)个.
根据题意,得80m+50(50-m)≤3000,
解得m≤16.
因为m为正整数,所以m的最大值为16.
答:篮球最多可购买16个.
五、(本大题共2小题,每小题10分,满分20分)
19.在如图所示的正方形网格中,每个小正方形的边长都为1个单位长度,三角形ABC的顶点都在正方形网格的格点上,将三角形ABC向上平移m个单位长度,再向右平移n个单位长度,平移后得到三角形A'B'C',其中图中直线l上的点A'是点A的对应点.
(1)画出平移后得到的三角形A'B'C';
(2)m+n= 8 ;
(3)在直线l上存在一点D,使A',B',C',D所围成的四边形的面积为6,请在直线l上画出所有符合要求的格点D.
解:(1)如图所示,三角形A'B'C'即为所求.
(3)如图所示,点D即为所求.
20.先化简:,再请从-2,-1,0,1中选一个你认为合适的数作为x的值,代入求值.
解:.
因为x≠±1且x≠-2,所以x=0,
所以原式=-1.
六、(满分12分)
21.我们在解题时,经常会遇到“数的平方”,那么你有简便方法吗 这里,我们以“两位数的平方”为例,请观察下列各式的规律,回答问题:
262=(26+6)×20+62;
372=(37+7)×30+72;
432=(43+3)×40+32;
…
(1)请根据上述规律填空:682= (68+8)×60+82 .
(2)我们知道,任何一个两位数(个数上的数字为n,十位上的数字为m)都可以表示为10m+n,根据上述规律写出:(10m+n)2= (10m+n+n)×10m+n2 ,并用所学知识说明你的结论的正确性.
(3)利用上述结论,简便计算982.
解:(2)证明:因为(10m+n)2=(10m)2+2×10m×n+n2=100m2+20mn+n2,
(10m+n+n)×10m+n2=100m2+20mn+n2,
所以(10m+n)2=(10m+n+n)×10m+n2.
(3)982=(98+8)×90+82=9604.
七、(满分12分)
22.为抗击新型冠状病毒肺炎疫情,某公司承担生产8800万个口罩的任务,该公司有A,B两个生产口罩的车间,A车间每天生产的口罩数量是B车间的1.2倍,A,B两车间共同生产一半后,A车间被抽调生产其他急需用品,剩下的全部由B车间单独完成,结果前后共用16天完成.
(1)求A,B两车间每天分别能生产口罩多少万个
(2)如果A车间每生产1万个口罩可创造利润1.5万元,B车间每生产1万个口罩可创造利润1.2万元,求该公司生产这批口罩共创造利润多少万元
解:(1)设B车间每天能生产口罩x万个,则A车间每天能生产口罩1.2x万个.
由题意得=16,解得x=400.
经检验,x=400是原分式方程的解,且符合题意,
所以1.2x=480.
答:A车间每天能生产口罩480万个,B车间每天能生产口罩400万个.
(2)1.2×400×16+1.5×(8800-400×16)=11280(万元).
答:该公司生产这批口罩共创造利润11280万元.
八、(满分14分)
23.问题情境:
在综合与实践课上,同学们以“一个含30°角的直角三角尺和三条平行线”为背景开展数学活动.如图1,已知直线a,b,c和直角三角形ABC,a∥b∥c,∠BCA=90°,∠BAC=30°,∠ABC=60°.
操作发现:
(1)在图1中,∠1=46°,请求出∠2的大小.
(2)创新小组的同学把直线a向上平移,并把∠2的位置改变,点B在直线c上,如图2,求∠2-∠1的大小.
实践探究:
(3)拓展小组在创新小组发现结论的基础上,将图2中的图形继续变化得到图3,点C在直线c上,AC平分∠BAM,此时你发现图3中的∠1与∠2有什么关系 请说明理由.
解:(1)如图,因为∠BCA=90°,
所以∠1+∠ACN=90°.
因为∠1=46°,所以∠ACN=90°-46°=44°.
因为a∥b,所以∠2=∠ACN=44°.
(2)因为a∥c,所以∠2+∠ABD=180°,
所以∠2=180°-∠ABD.
因为b∥c,所以∠DBC=∠1.
因为∠ABC=∠DBC+∠ABD=60°,
所以∠1+∠ABD=60°,所以∠1=60°-∠ABD,
所以∠2-∠1=180°-∠ABD-(60°-∠ABD)=120°.
(3)∠1=∠2.
理由:因为a∥c,所以∠2=∠BCE.
因为a∥b,所以∠1=∠BAM.
因为∠BAC=30°,AC平分∠BAM,
所以∠CAM=∠BAC=30°,∠BAM=2∠BAC=60°,
所以∠ECA=30°,∠1=∠BAM=60°.
因为∠BCA=90°,
所以∠2=∠BCE=90°-30°=60°,所以∠1=∠2.
同课章节目录
