沪科版数学七年级下册期末综合测评卷(二)(含答案)
文档属性
| 名称 | 沪科版数学七年级下册期末综合测评卷(二)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-04 13:04:11 | ||
图片预览




文档简介
沪科版数学七年级下册期末综合测评卷(二)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.在实数4,39,-π2,4.5050050005…中,不是无理数的是( )
A.4 B.39
C.-π2 D.4.5050050005…
2.若m>n>0,则下列结论正确的是( )
A.-2m>-2n B.m-2C.m>n D.12m<12n
3.如图,在直角三角板ABC中,∠C=90°,∠ABC=30°,顶点A,B分别在直线m,n上,边BC交直线m于点D.若m∥n,且∠CAD=25°,则∠α的度数为( )
A.105° B.115°
C.125° D.135°
4.已知2x=5,2y=10,则23x-2y=( )
A.12 B.25
C.54 D.-5
5.下列说法:①相等的角是对顶角;②三条直线两两相交,最少有三个交点;③在同一平面内,过一点有且只有一条直线与已知直线垂直;④在同一平面内,垂直于同一条直线的两条直线互相平行.其中正确的说法有( )
A.4个 B.3个
C.2个 D.1个
6.如果(x+a)(x+b)的结果中不含x的项,那么a,b满足( )
A.a=0 B.b=0
C.a=b D.a=-b
7.化简a-b2a·aa-b的结果是( )
A.a-b B.a+b
C.1a-b D.1a+b
8.比较7-1与72的大小,结果是( )
A.7-1>72 B.7-1<72
C.7-1=72 D.无法确定
9.若不等式组3x+1>0,x+a≤2恰好有两个整数解,则a的取值范围是( )
A.0≤a<1 B.0C.a>0 D.a<1
10.一副直角三角尺叠放如图1所示,现将含45°角的三角尺ADE固定不动,将含30°角的三角尺ABC绕顶点A顺时针转动(转动的角度小于180°),使两块三角尺至少有一组边互相平行,如图2所示,当∠BAD=15°时,BC∥DE.则∠BAD其他所有可能符合条件的度数有( )
A.45°,90°,105°,135° B.45°,60°,90°,135°
C.45°,60°,105°,135° D.35°,60°,120°,145°
二、填空题(本大题共4小题,每小题5分,满分20分)
11.要使分式3x-2有意义,则x的取值范围是 .?
12.生物研究表明,遗传信息大多储存在DNA分子上.已知一个DNA分子的直径约为0.00000002 cm.0.00000002用科学记数法表示为 .?
13.计算(x-y)(x+y)(x2+y2)(x4+y4)的结果是 .?
14.如图,AB∥CD,∠BAD和∠BCD的平分线交于点E,∠1=100°.
(1)若∠BAD=40°,则∠AEC的度数为 ;?
(2)若∠BAD=m°,则∠AEC的度数为 .?
三、(本大题共2小题,每小题8分,满分16分)
15.计算:(π-4)0+(-1)-2-|2-2|.
16.因式分解:4(x+y)2-16(x-y)2.
四、(本大题共2小题,每小题8分,满分16分)
17.求不等式组3(x-1)x-2的整数解.
18.如图,在正方形网格中,每个小正方形的边长均为1个单位长度,三角形ABC的三个顶点的位置如图所示.现将三角形ABC平移,使点C与点D重合,点A,B的对应点分别是E,F.
(1)在图中请画出三角形ABC平移后得到的三角形EFD;
(2)求三角形EFD的面积.
五、(本大题共2小题,每小题10分,满分20分)
19.先化简,再求值:a2-2ab+b2a2-b2÷a2-aba-2a+b,其中a,b满足(a-2)2+b+1=0.
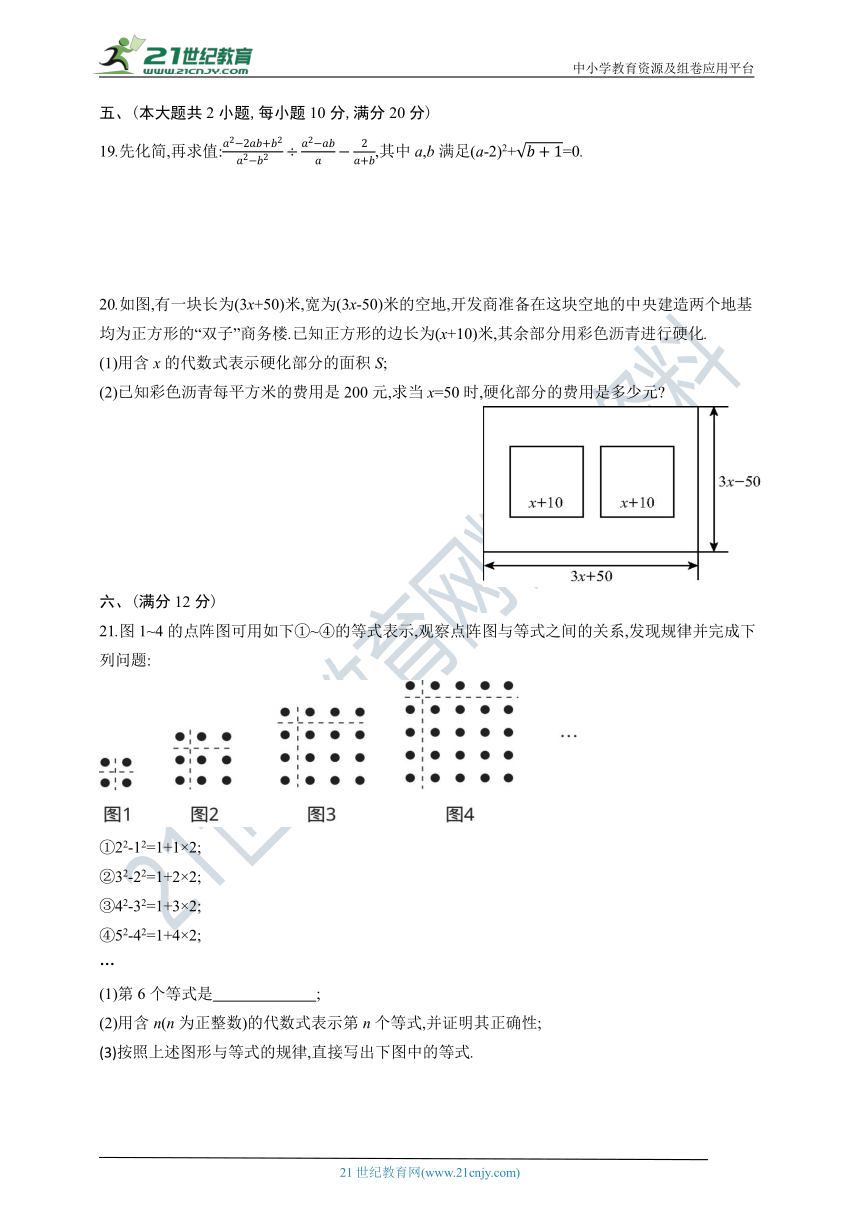
20.如图,有一块长为(3x+50)米,宽为(3x-50)米的空地,开发商准备在这块空地的中央建造两个地基均为正方形的“双子”商务楼.已知正方形的边长为(x+10)米,其余部分用彩色沥青进行硬化.
(1)用含x的代数式表示硬化部分的面积S;
(2)已知彩色沥青每平方米的费用是200元,求当x=50时,硬化部分的费用是多少元?
六、(满分12分)
21.图1~4的点阵图可用如下①~④的等式表示,观察点阵图与等式之间的关系,发现规律并完成下列问题:
①22-12=1+1×2;
②32-22=1+2×2;
③42-32=1+3×2;
④52-42=1+4×2;
…
(1)第6个等式是 ;?
(2)用含n(n为正整数)的代数式表示第n个等式,并证明其正确性;
(3)按照上述图形与等式的规律,直接写出下图中的等式.
七、(满分12分)
22.某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵5元,用360元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.
(1)求甲、乙两种商品每件的价格各是多少元?
(2)某商店计划购买这两种商品共40件,且投入的经费不超过1150元,那么最多可购买多少件甲种商品?
(3)李珍购买了甲、乙这两种商品,共用去145元钱,你知道他购买了甲、乙两种商品各多少件吗?
八、(满分14分)
23.(1)如图1,CM平分∠ACD,AM平分∠BAC,∠MAC+∠ACM=90°,请判断AB与CD的位置关系,并说明理由.
(2)如图2,∠M=90°且AB与CD的位置关系保持(1)中的不变,当直角顶点M移动时,问∠BAM与∠MCD是否存在确定的数量关系?并说明理由.
(3)如图3,G为线段AC上一个定点,H为直线CD上一个动点,且AB与CD的位置关系保持(1)中的不变,当点H在射线CD上运动时(点C除外),∠CGH,∠CHG与∠BAC有何数量关系?并说明理由.
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
1.在实数4,39,-π2,4.5050050005…中,不是无理数的是( A )
A.4 B.39
C.-π2 D.4.5050050005…
2.若m>n>0,则下列结论正确的是( C )
A.-2m>-2n B.m-2C.m>n D.12m<12n
3.如图,在直角三角板ABC中,∠C=90°,∠ABC=30°,顶点A,B分别在直线m,n上,边BC交直线m于点D.若m∥n,且∠CAD=25°,则∠α的度数为( B )
A.105° B.115°
C.125° D.135°
4.已知2x=5,2y=10,则23x-2y=( C )
A.12 B.25
C.54 D.-5
5.下列说法:①相等的角是对顶角;②三条直线两两相交,最少有三个交点;③在同一平面内,过一点有且只有一条直线与已知直线垂直;④在同一平面内,垂直于同一条直线的两条直线互相平行.其中正确的说法有( C )
A.4个 B.3个
C.2个 D.1个
6.如果(x+a)(x+b)的结果中不含x的项,那么a,b满足( D )
A.a=0 B.b=0
C.a=b D.a=-b
7.化简a-b2a·aa-b的结果是( B )
A.a-b B.a+b
C.1a-b D.1a+b
8.比较7-1与72的大小,结果是( A )
A.7-1>72 B.7-1<72
C.7-1=72 D.无法确定
9.若不等式组3x+1>0,x+a≤2恰好有两个整数解,则a的取值范围是( B )
A.0≤a<1 B.0C.a>0 D.a<1
【解析】解不等式组,得-1310.一副直角三角尺叠放如图1所示,现将含45°角的三角尺ADE固定不动,将含30°角的三角尺ABC绕顶点A顺时针转动(转动的角度小于180°),使两块三角尺至少有一组边互相平行,如图2所示,当∠BAD=15°时,BC∥DE.则∠BAD其他所有可能符合条件的度数有( C )
A.45°,90°,105°,135° B.45°,60°,90°,135°
C.45°,60°,105°,135° D.35°,60°,120°,145°
【解析】当AC∥DE时,∠BAD=45°;
当BC∥AD时,∠DAB=60°;
当BC∥AE时,∠BAD=105°;
当AB∥DE时,∠BAD=135°.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.要使分式3x-2有意义,则x的取值范围是 x>2 .?
12.生物研究表明,遗传信息大多储存在DNA分子上.已知一个DNA分子的直径约为0.00000002 cm.0.00000002用科学记数法表示为 2×10-8 .?
13.计算(x-y)(x+y)(x2+y2)(x4+y4)的结果是 x8-y8 .?
14.如图,AB∥CD,∠BAD和∠BCD的平分线交于点E,∠1=100°.
(1)若∠BAD=40°,则∠AEC的度数为 60° ;?
(2)若∠BAD=m°,则∠AEC的度数为 .?
【解析】过点E向左作射线EF∥AB.(1)因为AB∥CD,所以EF∥CD,所以∠BAE=∠AEF,∠FEC=∠ECD.因为∠1=100°,所以∠BCD=180°-∠1=80°.因为∠BAD和∠BCD的平分线交于点E,∠BAD=40°,所以∠BAE=12∠BAD=20°,∠ECD=12∠BCD=40°,所以∠AEC=∠AEF+∠FEC=∠BAE+∠ECD=60°.(2)由(1)得∠BAE=∠AEF,∠FEC=∠ECD,∠BCD=80°,所以∠BAE=12∠BAD=m°2,∠ECD=12∠BCD=40°,所以∠AEC=40°+m°2.
三、(本大题共2小题,每小题8分,满分16分)
15.计算:(π-4)0+(-1)-2-|2-2|.
解:原式=1+1-(2-2)=2-2+2=2.
16.因式分解:4(x+y)2-16(x-y)2.
解:4(x+y)2-16(x-y)2
=4[(x+y)2-4(x-y)2]
=4(x+y+2x-2y)(x+y-2x+2y)
=4(3x-y)(3y-x).
四、(本大题共2小题,每小题8分,满分16分)
17.求不等式组3(x-1)x-2的整数解.
解:3(x-1)x-2, ②
解不等式①,得x<2;
解不等式②,得x>-32,
所以不等式组的解集为-32所以不等式组的整数解是-1,0,1.
18.如图,在正方形网格中,每个小正方形的边长均为1个单位长度,三角形ABC的三个顶点的位置如图所示.现将三角形ABC平移,使点C与点D重合,点A,B的对应点分别是E,F.
(1)在图中请画出三角形ABC平移后得到的三角形EFD;
(2)求三角形EFD的面积.
解:(1)作图略.
(2)S三角形EFD=4×6-12×1×3-12×3×4-12×3×6=152.
五、(本大题共2小题,每小题10分,满分20分)
19.先化简,再求值:a2-2ab+b2a2-b2÷a2-aba-2a+b,其中a,b满足(a-2)2+b+1=0.
解:a2-2ab+b2a2-b2÷a2-aba-2a+b=(a-b)2(a+b)(a-b)·aa(a-b)-2a+b=1a+b-2a+b=-1a+b.
因为a,b满足(a-2)2+b+1=0,
所以a-2=0,b+1=0,解得 a=2,b=-1,
所以原式=-12-1=-1.
20.如图,有一块长为(3x+50)米,宽为(3x-50)米的空地,开发商准备在这块空地的中央建造两个地基均为正方形的“双子”商务楼.已知正方形的边长为(x+10)米,其余部分用彩色沥青进行硬化.
(1)用含x的代数式表示硬化部分的面积S;
(2)已知彩色沥青每平方米的费用是200元,求当x=50时,硬化部分的费用是多少元?
解:(1)S=(3x+50)(3x-50)-2(x+10)2
=9x2-2500-2(x2+20x+100)
=9x2-2500-2x2-40x-200
=7x2-40x-2700.
(2)当x=50时,S=7×502-40×50-2700=12800,
所以硬化部分的面积为12800米2,
所以硬化部分的费用为200×12800=2560000(元).
六、(满分12分)
21.图1~4的点阵图可用如下①~④的等式表示,观察点阵图与等式之间的关系,发现规律并完成下列问题:
①22-12=1+1×2;
②32-22=1+2×2;
③42-32=1+3×2;
④52-42=1+4×2;
…
(1)第6个等式是 72-62=1+6×2 ;?
(2)用含n(n为正整数)的代数式表示第n个等式,并证明其正确性;
(3)按照上述图形与等式的规律,直接写出下图中的等式.
解:(2)(n+1)2-n2=1+2n.
证明:左边=n2+2n+1-n2=2n+1=右边,
所以等式成立.
(3)52-32=4+6×2.(或52-22=9+6×2)
七、(满分12分)
22.某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵5元,用360元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.
(1)求甲、乙两种商品每件的价格各是多少元?
(2)某商店计划购买这两种商品共40件,且投入的经费不超过1150元,那么最多可购买多少件甲种商品?
(3)李珍购买了甲、乙这两种商品,共用去145元钱,你知道他购买了甲、乙两种商品各多少件吗?
解:(1)设每件乙种商品的价格为x元,则每件甲种商品的价格为(x+5)元.
依题意,得360x+5=300x,解得x=25,
经检验,x=25是原分式方程的解,且符合题意,
所以x+5=30.
答:每件甲种商品的价格为30元,每件乙种商品的价格为25元.
(2)设购买m件甲种商品,则购买(40-m)件乙种商品.
依题意,得30m+25(40-m)≤1150,解得m≤30.
答:最多可购买30件甲种商品.
(3)设购买了a件甲种商品,b件乙种商品.
依题意,得30a+25b=145,所以b=29-6a5.
因为a,b均为正整数,所以a=4,b=1.
答:李珍购买了4件甲种商品,1件乙种商品.
八、(满分14分)
23.(1)如图1,CM平分∠ACD,AM平分∠BAC,∠MAC+∠ACM=90°,请判断AB与CD的位置关系,并说明理由.
(2)如图2,∠M=90°且AB与CD的位置关系保持(1)中的不变,当直角顶点M移动时,问∠BAM与∠MCD是否存在确定的数量关系?并说明理由.
(3)如图3,G为线段AC上一个定点,H为直线CD上一个动点,且AB与CD的位置关系保持(1)中的不变,当点H在射线CD上运动时(点C除外),∠CGH,∠CHG与∠BAC有何数量关系?并说明理由.
解:(1)AB∥CD.
理由:因为CM平分∠ACD,AM平分∠BAC,
所以∠BAC=2∠MAC,∠ACD=2∠ACM.
因为∠MAC+∠ACM=90°,
所以∠BAC+∠ACD=180°,所以AB∥CD.
(2)存在,∠BAM+∠MCD=90°.
理由:过点M作MF∥AB,交AC于点F.
因为AB∥CD,所以MF∥CD,
所以∠BAM=∠AMF,∠FMC=∠MCD.
因为∠AMC=∠AMF+∠FMC=90°,
所以∠BAM+∠MCD=90°.
(3)∠CGH+∠CHG=∠BAC.
理由:过点G向左作射线GP∥AB.
因为AB∥CD,所以GP∥CD,
所以∠BAC=∠PGC,∠CHG=∠PGH,
因为∠PGC=∠PGH+∠CGH=∠CHG+∠CGH,
所以∠BAC=∠CHG+∠CGH.
一、选择题(本大题共10小题,每小题4分,满分40分)
1.在实数4,39,-π2,4.5050050005…中,不是无理数的是( )
A.4 B.39
C.-π2 D.4.5050050005…
2.若m>n>0,则下列结论正确的是( )
A.-2m>-2n B.m-2
3.如图,在直角三角板ABC中,∠C=90°,∠ABC=30°,顶点A,B分别在直线m,n上,边BC交直线m于点D.若m∥n,且∠CAD=25°,则∠α的度数为( )
A.105° B.115°
C.125° D.135°
4.已知2x=5,2y=10,则23x-2y=( )
A.12 B.25
C.54 D.-5
5.下列说法:①相等的角是对顶角;②三条直线两两相交,最少有三个交点;③在同一平面内,过一点有且只有一条直线与已知直线垂直;④在同一平面内,垂直于同一条直线的两条直线互相平行.其中正确的说法有( )
A.4个 B.3个
C.2个 D.1个
6.如果(x+a)(x+b)的结果中不含x的项,那么a,b满足( )
A.a=0 B.b=0
C.a=b D.a=-b
7.化简a-b2a·aa-b的结果是( )
A.a-b B.a+b
C.1a-b D.1a+b
8.比较7-1与72的大小,结果是( )
A.7-1>72 B.7-1<72
C.7-1=72 D.无法确定
9.若不等式组3x+1>0,x+a≤2恰好有两个整数解,则a的取值范围是( )
A.0≤a<1 B.0
10.一副直角三角尺叠放如图1所示,现将含45°角的三角尺ADE固定不动,将含30°角的三角尺ABC绕顶点A顺时针转动(转动的角度小于180°),使两块三角尺至少有一组边互相平行,如图2所示,当∠BAD=15°时,BC∥DE.则∠BAD其他所有可能符合条件的度数有( )
A.45°,90°,105°,135° B.45°,60°,90°,135°
C.45°,60°,105°,135° D.35°,60°,120°,145°
二、填空题(本大题共4小题,每小题5分,满分20分)
11.要使分式3x-2有意义,则x的取值范围是 .?
12.生物研究表明,遗传信息大多储存在DNA分子上.已知一个DNA分子的直径约为0.00000002 cm.0.00000002用科学记数法表示为 .?
13.计算(x-y)(x+y)(x2+y2)(x4+y4)的结果是 .?
14.如图,AB∥CD,∠BAD和∠BCD的平分线交于点E,∠1=100°.
(1)若∠BAD=40°,则∠AEC的度数为 ;?
(2)若∠BAD=m°,则∠AEC的度数为 .?
三、(本大题共2小题,每小题8分,满分16分)
15.计算:(π-4)0+(-1)-2-|2-2|.
16.因式分解:4(x+y)2-16(x-y)2.
四、(本大题共2小题,每小题8分,满分16分)
17.求不等式组3(x-1)
18.如图,在正方形网格中,每个小正方形的边长均为1个单位长度,三角形ABC的三个顶点的位置如图所示.现将三角形ABC平移,使点C与点D重合,点A,B的对应点分别是E,F.
(1)在图中请画出三角形ABC平移后得到的三角形EFD;
(2)求三角形EFD的面积.
五、(本大题共2小题,每小题10分,满分20分)
19.先化简,再求值:a2-2ab+b2a2-b2÷a2-aba-2a+b,其中a,b满足(a-2)2+b+1=0.
20.如图,有一块长为(3x+50)米,宽为(3x-50)米的空地,开发商准备在这块空地的中央建造两个地基均为正方形的“双子”商务楼.已知正方形的边长为(x+10)米,其余部分用彩色沥青进行硬化.
(1)用含x的代数式表示硬化部分的面积S;
(2)已知彩色沥青每平方米的费用是200元,求当x=50时,硬化部分的费用是多少元?
六、(满分12分)
21.图1~4的点阵图可用如下①~④的等式表示,观察点阵图与等式之间的关系,发现规律并完成下列问题:
①22-12=1+1×2;
②32-22=1+2×2;
③42-32=1+3×2;
④52-42=1+4×2;
…
(1)第6个等式是 ;?
(2)用含n(n为正整数)的代数式表示第n个等式,并证明其正确性;
(3)按照上述图形与等式的规律,直接写出下图中的等式.
七、(满分12分)
22.某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵5元,用360元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.
(1)求甲、乙两种商品每件的价格各是多少元?
(2)某商店计划购买这两种商品共40件,且投入的经费不超过1150元,那么最多可购买多少件甲种商品?
(3)李珍购买了甲、乙这两种商品,共用去145元钱,你知道他购买了甲、乙两种商品各多少件吗?
八、(满分14分)
23.(1)如图1,CM平分∠ACD,AM平分∠BAC,∠MAC+∠ACM=90°,请判断AB与CD的位置关系,并说明理由.
(2)如图2,∠M=90°且AB与CD的位置关系保持(1)中的不变,当直角顶点M移动时,问∠BAM与∠MCD是否存在确定的数量关系?并说明理由.
(3)如图3,G为线段AC上一个定点,H为直线CD上一个动点,且AB与CD的位置关系保持(1)中的不变,当点H在射线CD上运动时(点C除外),∠CGH,∠CHG与∠BAC有何数量关系?并说明理由.
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
1.在实数4,39,-π2,4.5050050005…中,不是无理数的是( A )
A.4 B.39
C.-π2 D.4.5050050005…
2.若m>n>0,则下列结论正确的是( C )
A.-2m>-2n B.m-2
3.如图,在直角三角板ABC中,∠C=90°,∠ABC=30°,顶点A,B分别在直线m,n上,边BC交直线m于点D.若m∥n,且∠CAD=25°,则∠α的度数为( B )
A.105° B.115°
C.125° D.135°
4.已知2x=5,2y=10,则23x-2y=( C )
A.12 B.25
C.54 D.-5
5.下列说法:①相等的角是对顶角;②三条直线两两相交,最少有三个交点;③在同一平面内,过一点有且只有一条直线与已知直线垂直;④在同一平面内,垂直于同一条直线的两条直线互相平行.其中正确的说法有( C )
A.4个 B.3个
C.2个 D.1个
6.如果(x+a)(x+b)的结果中不含x的项,那么a,b满足( D )
A.a=0 B.b=0
C.a=b D.a=-b
7.化简a-b2a·aa-b的结果是( B )
A.a-b B.a+b
C.1a-b D.1a+b
8.比较7-1与72的大小,结果是( A )
A.7-1>72 B.7-1<72
C.7-1=72 D.无法确定
9.若不等式组3x+1>0,x+a≤2恰好有两个整数解,则a的取值范围是( B )
A.0≤a<1 B.0
【解析】解不等式组,得-13
A.45°,90°,105°,135° B.45°,60°,90°,135°
C.45°,60°,105°,135° D.35°,60°,120°,145°
【解析】当AC∥DE时,∠BAD=45°;
当BC∥AD时,∠DAB=60°;
当BC∥AE时,∠BAD=105°;
当AB∥DE时,∠BAD=135°.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.要使分式3x-2有意义,则x的取值范围是 x>2 .?
12.生物研究表明,遗传信息大多储存在DNA分子上.已知一个DNA分子的直径约为0.00000002 cm.0.00000002用科学记数法表示为 2×10-8 .?
13.计算(x-y)(x+y)(x2+y2)(x4+y4)的结果是 x8-y8 .?
14.如图,AB∥CD,∠BAD和∠BCD的平分线交于点E,∠1=100°.
(1)若∠BAD=40°,则∠AEC的度数为 60° ;?
(2)若∠BAD=m°,则∠AEC的度数为 .?
【解析】过点E向左作射线EF∥AB.(1)因为AB∥CD,所以EF∥CD,所以∠BAE=∠AEF,∠FEC=∠ECD.因为∠1=100°,所以∠BCD=180°-∠1=80°.因为∠BAD和∠BCD的平分线交于点E,∠BAD=40°,所以∠BAE=12∠BAD=20°,∠ECD=12∠BCD=40°,所以∠AEC=∠AEF+∠FEC=∠BAE+∠ECD=60°.(2)由(1)得∠BAE=∠AEF,∠FEC=∠ECD,∠BCD=80°,所以∠BAE=12∠BAD=m°2,∠ECD=12∠BCD=40°,所以∠AEC=40°+m°2.
三、(本大题共2小题,每小题8分,满分16分)
15.计算:(π-4)0+(-1)-2-|2-2|.
解:原式=1+1-(2-2)=2-2+2=2.
16.因式分解:4(x+y)2-16(x-y)2.
解:4(x+y)2-16(x-y)2
=4[(x+y)2-4(x-y)2]
=4(x+y+2x-2y)(x+y-2x+2y)
=4(3x-y)(3y-x).
四、(本大题共2小题,每小题8分,满分16分)
17.求不等式组3(x-1)
解:3(x-1)
解不等式①,得x<2;
解不等式②,得x>-32,
所以不等式组的解集为-32
18.如图,在正方形网格中,每个小正方形的边长均为1个单位长度,三角形ABC的三个顶点的位置如图所示.现将三角形ABC平移,使点C与点D重合,点A,B的对应点分别是E,F.
(1)在图中请画出三角形ABC平移后得到的三角形EFD;
(2)求三角形EFD的面积.
解:(1)作图略.
(2)S三角形EFD=4×6-12×1×3-12×3×4-12×3×6=152.
五、(本大题共2小题,每小题10分,满分20分)
19.先化简,再求值:a2-2ab+b2a2-b2÷a2-aba-2a+b,其中a,b满足(a-2)2+b+1=0.
解:a2-2ab+b2a2-b2÷a2-aba-2a+b=(a-b)2(a+b)(a-b)·aa(a-b)-2a+b=1a+b-2a+b=-1a+b.
因为a,b满足(a-2)2+b+1=0,
所以a-2=0,b+1=0,解得 a=2,b=-1,
所以原式=-12-1=-1.
20.如图,有一块长为(3x+50)米,宽为(3x-50)米的空地,开发商准备在这块空地的中央建造两个地基均为正方形的“双子”商务楼.已知正方形的边长为(x+10)米,其余部分用彩色沥青进行硬化.
(1)用含x的代数式表示硬化部分的面积S;
(2)已知彩色沥青每平方米的费用是200元,求当x=50时,硬化部分的费用是多少元?
解:(1)S=(3x+50)(3x-50)-2(x+10)2
=9x2-2500-2(x2+20x+100)
=9x2-2500-2x2-40x-200
=7x2-40x-2700.
(2)当x=50时,S=7×502-40×50-2700=12800,
所以硬化部分的面积为12800米2,
所以硬化部分的费用为200×12800=2560000(元).
六、(满分12分)
21.图1~4的点阵图可用如下①~④的等式表示,观察点阵图与等式之间的关系,发现规律并完成下列问题:
①22-12=1+1×2;
②32-22=1+2×2;
③42-32=1+3×2;
④52-42=1+4×2;
…
(1)第6个等式是 72-62=1+6×2 ;?
(2)用含n(n为正整数)的代数式表示第n个等式,并证明其正确性;
(3)按照上述图形与等式的规律,直接写出下图中的等式.
解:(2)(n+1)2-n2=1+2n.
证明:左边=n2+2n+1-n2=2n+1=右边,
所以等式成立.
(3)52-32=4+6×2.(或52-22=9+6×2)
七、(满分12分)
22.某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵5元,用360元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.
(1)求甲、乙两种商品每件的价格各是多少元?
(2)某商店计划购买这两种商品共40件,且投入的经费不超过1150元,那么最多可购买多少件甲种商品?
(3)李珍购买了甲、乙这两种商品,共用去145元钱,你知道他购买了甲、乙两种商品各多少件吗?
解:(1)设每件乙种商品的价格为x元,则每件甲种商品的价格为(x+5)元.
依题意,得360x+5=300x,解得x=25,
经检验,x=25是原分式方程的解,且符合题意,
所以x+5=30.
答:每件甲种商品的价格为30元,每件乙种商品的价格为25元.
(2)设购买m件甲种商品,则购买(40-m)件乙种商品.
依题意,得30m+25(40-m)≤1150,解得m≤30.
答:最多可购买30件甲种商品.
(3)设购买了a件甲种商品,b件乙种商品.
依题意,得30a+25b=145,所以b=29-6a5.
因为a,b均为正整数,所以a=4,b=1.
答:李珍购买了4件甲种商品,1件乙种商品.
八、(满分14分)
23.(1)如图1,CM平分∠ACD,AM平分∠BAC,∠MAC+∠ACM=90°,请判断AB与CD的位置关系,并说明理由.
(2)如图2,∠M=90°且AB与CD的位置关系保持(1)中的不变,当直角顶点M移动时,问∠BAM与∠MCD是否存在确定的数量关系?并说明理由.
(3)如图3,G为线段AC上一个定点,H为直线CD上一个动点,且AB与CD的位置关系保持(1)中的不变,当点H在射线CD上运动时(点C除外),∠CGH,∠CHG与∠BAC有何数量关系?并说明理由.
解:(1)AB∥CD.
理由:因为CM平分∠ACD,AM平分∠BAC,
所以∠BAC=2∠MAC,∠ACD=2∠ACM.
因为∠MAC+∠ACM=90°,
所以∠BAC+∠ACD=180°,所以AB∥CD.
(2)存在,∠BAM+∠MCD=90°.
理由:过点M作MF∥AB,交AC于点F.
因为AB∥CD,所以MF∥CD,
所以∠BAM=∠AMF,∠FMC=∠MCD.
因为∠AMC=∠AMF+∠FMC=90°,
所以∠BAM+∠MCD=90°.
(3)∠CGH+∠CHG=∠BAC.
理由:过点G向左作射线GP∥AB.
因为AB∥CD,所以GP∥CD,
所以∠BAC=∠PGC,∠CHG=∠PGH,
因为∠PGC=∠PGH+∠CGH=∠CHG+∠CGH,
所以∠BAC=∠CHG+∠CGH.
同课章节目录
