11.2.2三角形的外角人教版数学教材八年级上册(共16张ppt)
文档属性
| 名称 | 11.2.2三角形的外角人教版数学教材八年级上册(共16张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-06 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
人教版数学教材八年级上
11.2.2
三角形的外角
2
.体会几何中不等关系的简单证明;
3.引导学生从内和外、相等和不等的
不同角度对三角形作更全面的思考.
1.掌握三角形内角和定理的两个
推论及其证明;
教学难点:
三角形外角和定理的证明方法.
教学重点:
三角形外角和定理的证明思路及应用.
学习
目标
1.什么是三角形的外角?
预习探路
?
2.三角形的外角具有哪些性质,是如何证明的?
咦,这哥俩怎么了?
三角形都长头发了
谁让你光注意三角形的里边呢
外边还有啥?
还有一个角呢!
创设情境
1
关注三角形的外角
B
A
C
D
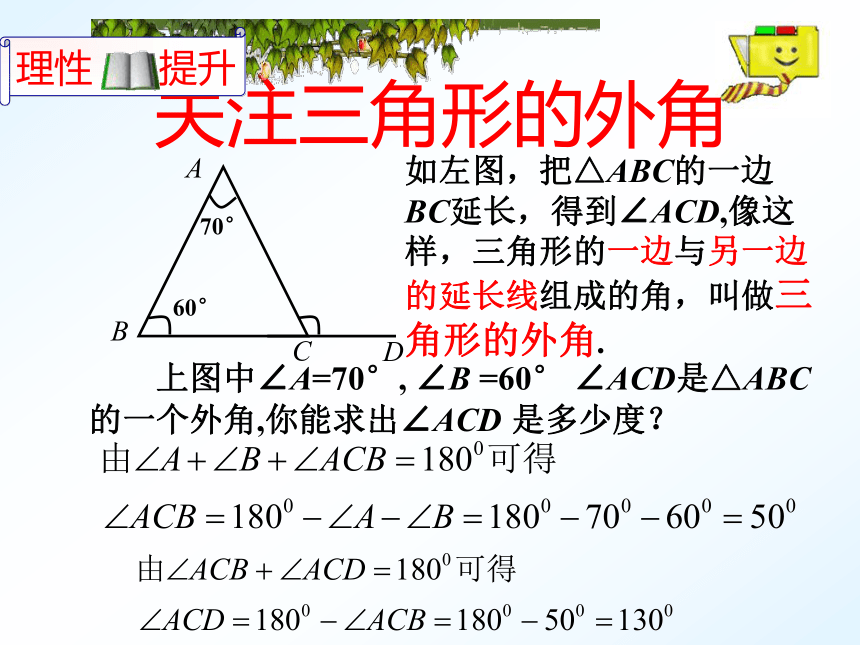
如左图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
60°
70°
上图中∠A=70°,
∠B
=60°
∠ACD是△ABC的一个外角,你能求出∠ACD
是多少度?
理性
提升
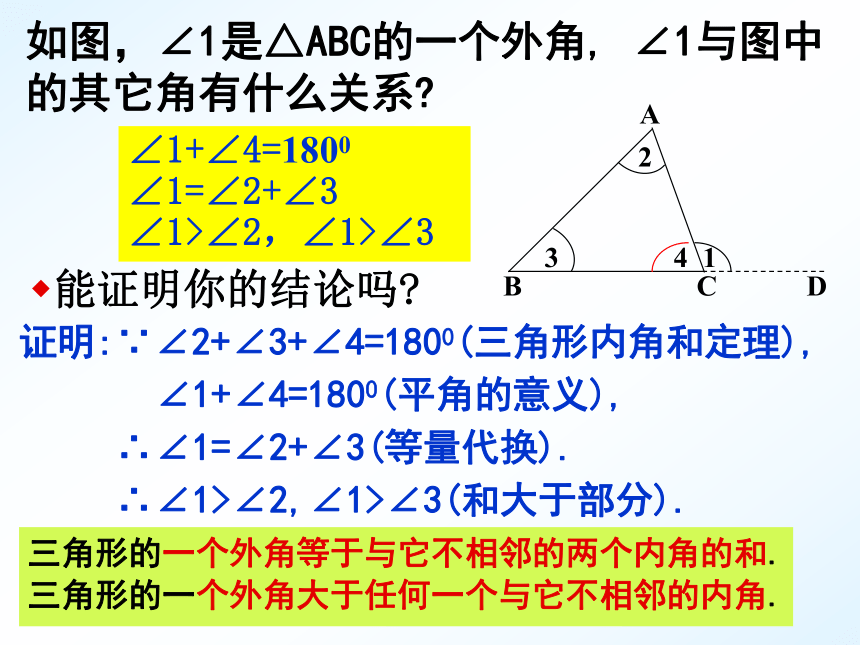
如图,∠1是△ABC的一个外角,
∠1与图中的其它角有什么关系?
∠1+∠4=1800
∠1=∠2+∠3
∠1>∠2,∠1>∠3
证明:∵∠2+∠3+∠4=1800(三角形内角和定理),
∠1+∠4=1800(平角的意义),
∴∠1=∠2+∠3(等量代换).
∴∠1>∠2,∠1>∠3(和大于部分).
A
B
C
D
1
2
3
4
能证明你的结论吗?
三角形的一个外角等于与它不相邻的两个内角的和.
三角形的一个外角大于任何一个与它不相邻的内角.
A
C
D
B
E
·
·
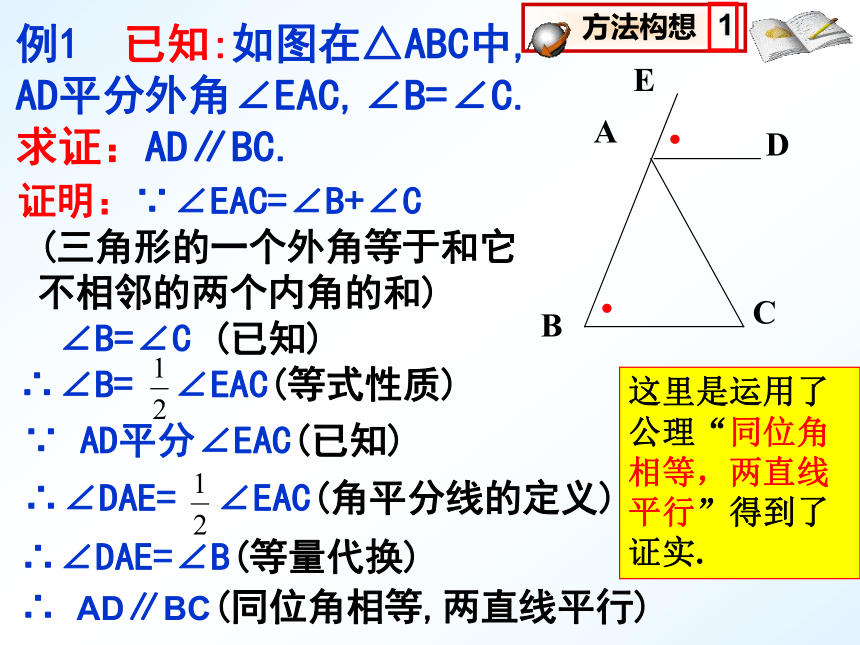
例1
已知:如图在△ABC中,
AD平分外角∠EAC,∠B=∠C.
求证:AD∥BC.
∵
AD平分∠EAC(已知)
∴∠DAE=
∠EAC(角平分线的定义)
∴∠DAE=∠B(等量代换)
∴
AD∥BC(同位角相等,两直线平行)
这里是运用了公理“同位角相等,两直线平行”得到了证实.
证明:∵∠EAC=∠B+∠C
(三角形的一个外角等于和它
不相邻的两个内角的和)
∠B=∠C
(已知)
∴∠B=
∠EAC(等式性质)
方法构想
1
例2
已知:如图,在△ABC中,
∠1是它的一个外角,
E为边
AC上一点,延长BC到D,连接DE.
求证:
∠1>∠2.
证明:∵
∠1是△ABC的
一个外角
(已知)
∴
∠1>∠3
(三角形的一个外角大于任何一个和它不相邻的内角)
∵∠3是△CDE的一个外角
(外角定义)
∴∠3>∠2
(三角形的一个外角大于任何一个和
它不相邻的内角)
∴
∠1>∠2
(不等式的性质)
C
A
B
F
1
3
4
5
E
D
2
例3
已知:国旗上的正五角星形如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.
解:∵∠1是△BDF的一个
外角(外角定义)
∴∠1=∠B+∠D(三角形的一个
外角等于和它不相邻的两个
内角的和)
又∵∠2是△EHC的一个外角(外角定义)
∴∠2=∠C+∠E(三角形的一个外角等于
和它不相邻的两个内角的和)
又∵∠A+∠1+∠2=180°(三角形内角和定理)
∴∠A+∠B+∠C+∠D+∠E
=180°(等式性质)
A
B
C
D
E
F
1
H
2
三角形内角和定理的推论:
推论1:
三角形的一个外角等于与它不相邻的两个内角的和.
推论2:
三角形的一个外角大于任何一个与它不相邻的内角.
A
B
C
D
1
2
3
4
在这里,我们通过三角形内角和定理直接推导出两个新定理.像这样,由一个公理或定理直接推出的定理,叫做这个公理或定理的推论.
推论可以当作定理使用.
小结归纳
1
已知:如图所示,在△ABC中,外角∠DCA=100°,∠A=45°.
求:∠B和∠ACB的大小.
A
B
C
D
解:∵
∠DCA是△ABC的一个外角(已知),
∠DCA=100°(已知),
∴
∠B=100°-45°=55°.(三角形的一个外角等于和它不相邻的两个内角的和).
又∵
∠DCA+∠BCA=180°(平角的意义).
∴
∠ACB=80°(等式的性质).
∠A=45°(已知),
行家伸伸手
已知:如图所示.
求证:(1)∠BDC>∠A;
(2)
∠BDC=∠A+∠B+∠C.
证明(1):∵
∠BDC是△DCE的一个外角
(外角定义),
∴
∠BDC>∠CED(三角形的一个外角大于和它不相邻的任何一个外角).
∴
∠DEC>∠A(三角形的一个外角大于和它不相邻的任何一个外角).
∴
∠BDC>∠A
(不等式的性质).
∵
∠DEC是△ABE的一个外角
(外角定义),
B
C
A
D
E
关注三角形的外角
当堂测试
1
已知:如图所示.
求证:(1)∠BDC>∠A;
(2)
∠BDC=∠A+∠B+∠C.
证明(2):∵
∠BDC是△DCE的一个外角
(外角定义),
∴
∠BDC
=∠C+∠CED(三角形的一个外角等于和它不相邻的两个内角的和).
∴
∠DEC=∠A+
∠B(三角形的一个外角等于和它不相邻的两个外角的和).
∴
∠BDC=∠A+∠B+∠C
(等式的性质).
∵
∠DEC是△ABE的一个外角
(外角定义),
B
C
A
D
E
关注三角形的外角
(2010.东营)如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数等于(
)
A.
50°
B.
30°
C.
20°
D.
15°
C
1
2
3
三角形内角和定理
:
推论1:
推论2:
推论3:
三角形三个内角的和等于1800.
三角形的一个外角等于与它不相邻
的两个内角的和.
三角形的一个外角大于任何一个与
它不相邻的内角.
直角三角形的两锐角互余.
小结归纳
2
独立
作业
练习题
作业
人教版数学教材八年级上
11.2.2
三角形的外角
2
.体会几何中不等关系的简单证明;
3.引导学生从内和外、相等和不等的
不同角度对三角形作更全面的思考.
1.掌握三角形内角和定理的两个
推论及其证明;
教学难点:
三角形外角和定理的证明方法.
教学重点:
三角形外角和定理的证明思路及应用.
学习
目标
1.什么是三角形的外角?
预习探路
?
2.三角形的外角具有哪些性质,是如何证明的?
咦,这哥俩怎么了?
三角形都长头发了
谁让你光注意三角形的里边呢
外边还有啥?
还有一个角呢!
创设情境
1
关注三角形的外角
B
A
C
D
如左图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
60°
70°
上图中∠A=70°,
∠B
=60°
∠ACD是△ABC的一个外角,你能求出∠ACD
是多少度?
理性
提升
如图,∠1是△ABC的一个外角,
∠1与图中的其它角有什么关系?
∠1+∠4=1800
∠1=∠2+∠3
∠1>∠2,∠1>∠3
证明:∵∠2+∠3+∠4=1800(三角形内角和定理),
∠1+∠4=1800(平角的意义),
∴∠1=∠2+∠3(等量代换).
∴∠1>∠2,∠1>∠3(和大于部分).
A
B
C
D
1
2
3
4
能证明你的结论吗?
三角形的一个外角等于与它不相邻的两个内角的和.
三角形的一个外角大于任何一个与它不相邻的内角.
A
C
D
B
E
·
·
例1
已知:如图在△ABC中,
AD平分外角∠EAC,∠B=∠C.
求证:AD∥BC.
∵
AD平分∠EAC(已知)
∴∠DAE=
∠EAC(角平分线的定义)
∴∠DAE=∠B(等量代换)
∴
AD∥BC(同位角相等,两直线平行)
这里是运用了公理“同位角相等,两直线平行”得到了证实.
证明:∵∠EAC=∠B+∠C
(三角形的一个外角等于和它
不相邻的两个内角的和)
∠B=∠C
(已知)
∴∠B=
∠EAC(等式性质)
方法构想
1
例2
已知:如图,在△ABC中,
∠1是它的一个外角,
E为边
AC上一点,延长BC到D,连接DE.
求证:
∠1>∠2.
证明:∵
∠1是△ABC的
一个外角
(已知)
∴
∠1>∠3
(三角形的一个外角大于任何一个和它不相邻的内角)
∵∠3是△CDE的一个外角
(外角定义)
∴∠3>∠2
(三角形的一个外角大于任何一个和
它不相邻的内角)
∴
∠1>∠2
(不等式的性质)
C
A
B
F
1
3
4
5
E
D
2
例3
已知:国旗上的正五角星形如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.
解:∵∠1是△BDF的一个
外角(外角定义)
∴∠1=∠B+∠D(三角形的一个
外角等于和它不相邻的两个
内角的和)
又∵∠2是△EHC的一个外角(外角定义)
∴∠2=∠C+∠E(三角形的一个外角等于
和它不相邻的两个内角的和)
又∵∠A+∠1+∠2=180°(三角形内角和定理)
∴∠A+∠B+∠C+∠D+∠E
=180°(等式性质)
A
B
C
D
E
F
1
H
2
三角形内角和定理的推论:
推论1:
三角形的一个外角等于与它不相邻的两个内角的和.
推论2:
三角形的一个外角大于任何一个与它不相邻的内角.
A
B
C
D
1
2
3
4
在这里,我们通过三角形内角和定理直接推导出两个新定理.像这样,由一个公理或定理直接推出的定理,叫做这个公理或定理的推论.
推论可以当作定理使用.
小结归纳
1
已知:如图所示,在△ABC中,外角∠DCA=100°,∠A=45°.
求:∠B和∠ACB的大小.
A
B
C
D
解:∵
∠DCA是△ABC的一个外角(已知),
∠DCA=100°(已知),
∴
∠B=100°-45°=55°.(三角形的一个外角等于和它不相邻的两个内角的和).
又∵
∠DCA+∠BCA=180°(平角的意义).
∴
∠ACB=80°(等式的性质).
∠A=45°(已知),
行家伸伸手
已知:如图所示.
求证:(1)∠BDC>∠A;
(2)
∠BDC=∠A+∠B+∠C.
证明(1):∵
∠BDC是△DCE的一个外角
(外角定义),
∴
∠BDC>∠CED(三角形的一个外角大于和它不相邻的任何一个外角).
∴
∠DEC>∠A(三角形的一个外角大于和它不相邻的任何一个外角).
∴
∠BDC>∠A
(不等式的性质).
∵
∠DEC是△ABE的一个外角
(外角定义),
B
C
A
D
E
关注三角形的外角
当堂测试
1
已知:如图所示.
求证:(1)∠BDC>∠A;
(2)
∠BDC=∠A+∠B+∠C.
证明(2):∵
∠BDC是△DCE的一个外角
(外角定义),
∴
∠BDC
=∠C+∠CED(三角形的一个外角等于和它不相邻的两个内角的和).
∴
∠DEC=∠A+
∠B(三角形的一个外角等于和它不相邻的两个外角的和).
∴
∠BDC=∠A+∠B+∠C
(等式的性质).
∵
∠DEC是△ABE的一个外角
(外角定义),
B
C
A
D
E
关注三角形的外角
(2010.东营)如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数等于(
)
A.
50°
B.
30°
C.
20°
D.
15°
C
1
2
3
三角形内角和定理
:
推论1:
推论2:
推论3:
三角形三个内角的和等于1800.
三角形的一个外角等于与它不相邻
的两个内角的和.
三角形的一个外角大于任何一个与
它不相邻的内角.
直角三角形的两锐角互余.
小结归纳
2
独立
作业
练习题
作业
